Похожие презентации:
Понятие и виды матриц
1.
«МАТРИЦЫ»2. ПЛАН
1. ПОНЯТИЕ И ВИДЫ МАТРИЦ2. СТРОКИ, СТОЛБЦЫ, ЭЛЕМЕНТЫ
И РАЗМЕР МАТРИЦ
3. ОПЕРАЦИИ НАД МАТРИЦАМИ
3. ОПРЕДЕЛЕНИЯ
МАТРИЦЕЙ НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНАЯ ИЛИКВАДРАТНАЯ ТАБЛИЦА, ЗАПОЛНЕННАЯ ЧИСЛАМИ.
ЧИСЛА, ЗАПОЛНЯЮЩИЕ МАТРИЦУ, НАЗЫВАЮТСЯ
ЭЛЕМЕНТАМИ МАТРИЦЫ.
4. ВИДЫ МАТРИЦ
412
17 29 Прямоугольная
матрица
30 36
3
22
Матрица-столбец
0
5
3 1 2
4 2 0 Квадратная
матрица
5 6 1
1
3 2 0
Матрица-строка
5. ПРИНЦИП НУМЕРАЦИИ СТРОК И СТОЛБЦОВ
СТРОКИ НУМЕРУЮТСЯ СВЕРХУВНИЗ, НАЧИНАЯ С № 1.
СТОЛБЦЫ НУМЕРУЮТСЯ СЛЕВА
НАПРАВО, НАЧИНАЯ С № 1.
6. СТРОКА И СТОЛБЕЦ
412
17 29
30 36 3-я строка
4
12
17 29
30 36 2-й столбец
7. РАЗМЕР МАТРИЦЫ
МАТРИЦА, ИМЕЮЩАЯm СТРОК И n
СТОЛБЦОВ, НАЗЫВАЕТСЯ МАТРИЦЕЙ
РАЗМЕРА
m НА n.
4
12
17 29 Матрица размера 3 на 2
(3 строки, 2 столбца)
30 36
8. ОБЩИЙ ВИД МАТРИЦЫ РАЗМЕРА m НА n
ОБЩИЙ ВИД МАТРИЦЫРАЗМЕРА M НА N
a11 a12
a21 a22
A
...
...
a
m1 am2
a1n
... a2n
... ...
... amn
...
9. ЭЛЕМЕНТ МАТРИЦЫ
4 Элемент a31 a-три-один 3012
17 29
(3-я строка,1-й столбец)
30 36
10. ДИАГОНАЛИ КВАДРАТНЫХ МАТРИЦ
3 1 24 2 0 Главная диагональ
5 6 1
3 1 2
4 2 0 Побочная диагональ
5 6 1
11. ТРЕУГОЛЬНЫЕ МАТРИЦЫ
Верхняя треугольная матрица3 1 2
0 2 0 (под главной диагональю стоят нули)
0 0 1
Нижняя треугольная матрица
3 0 0
1 2 0 (над главной диагональю стоят нули)
2 0 1
12. ЛЮБУЮ МАТРИЦУ МОЖНО УМНОЖИТЬ НА ЧИСЛО
3 1 2 15 5 105 4 2 0 20 10 0
5 6 1 25 30 5
13. МАТРИЦЫ ОДИНАКОВОГО РАЗМЕРА МОЖНО СКЛАДЫВАТЬ И ВЫЧИТАТЬ
3 1 2 8 5 54 2 0 7 3 14
3 8 1 5 2 5
2 3
0 14
4 7
14. ТРАНСПОНИРОВАНИЕ МАТРИЦЫ
412
Исходная
A 17 29
матрица (размер 3 на 2)
30 36
12 17 30 Транспонированная
A
матрица (размер 2 на 3)
4
29
36
T
15. УМНОЖЕНИЕ СТРОКИ НА СТОЛБЕЦ (СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ)
72 5 3 0 2 7 5 0 3 4 2
4
16. УМНОЖЕНИЕ МАТРИЦЫ НА СТОЛБЕЦ КАЖДАЯ СТРОКА МАТРИЦЫ СКАЛЯРНО УМНОЖАЕТСЯ НА СТОЛБЕЦ
3 1 2 8 3 8 1 7 2 2 214 2 0 7 4 8 2 7 0 2 46
5 6 1 2 5 8 6 7 1 2 4
17. Умножение матриц
УМНОЖЕНИЕ МАТРИЦПроизведение матриц А и В имеет смысл, если число столбцов в А
равно числу строк в В.
18.
Если матрицы А и В квадратные размером n х n, тоимеет смысл как произведение матриц АВ, так и
произведение матриц BA, причем размер этих
матриц такой же, как и у исходных сомножителей.
При этом в общем случае перемножения матриц
правило перестановочности не соблюдается, т.е.
АВ ≠ ВА.
19. ПРИМЕР УМНОЖЕНИЯ МАТРИЦ
3 1 2 8 14 2 0 7 2
5 6 1 2 3
3 8 1 7 2 2 3 1 1 2 2 3 21 5
4 8 2 7 0 2
4 1 2 2 0 3 46 8
5 8 6 7 1 2 5 1 6 2 1 3 4 4
20. УМНОЖЕНИЕ СТОЛБЦА НА СТРОКУ
7 27
0 2 5 3 0 2
4
4 2
7 5
0 5
4 5
14 35 21
0
0
0
8 20 12
7 3
0 3
4 3
21. ТИПЫ КВАДРАТНЫХ МАТРИЦ
1 0 0Единичная матрица
E 0 1 0
(размер 3 на 3)
0 0 1
0 0 0
Нулевая матрица
0 0 0 0
(размер 3 на 3)
0 0 0
22. СВОЙСТВО ЕДИНИЧНОЙ МАТРИЦЫ: A•E=E•A=A
5 7 4 1 0 0 5 7 43 6 8 0 1 0 3 6 8
11 4 0 0 0 1 11 4 0
1 0 0 5 7 4 5 7 4
0 1 0 3 6 8 3 6 8
0 0 1 11 4 0 11 4 0
23.
ОПРЕДЕЛИТЕЛИ24. ПЛАН
1. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙМАТРИЦЫ
2. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ
ДОПОЛНЕНИЯ
3. СПОСОБЫ ВЫЧИСЛЕНИЯ
ОПРЕДЕЛИТЕЛЕЙ
4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
25. ОПРЕДЕЛИТЕЛЬ КВАДРАТНОЙ МАТРИЦЫ
26. ОБОЗНАЧЕНИЯ
КВАДРАТНАЯ МАТРИЦА n-го ПОРЯДКАa11
A
a
n1
a1n
ann
ОБОЗНАЧЕНИЯ ОПРЕДЕЛИТЕЛЯ МАТРИЦЫ
a11
a1n
an1
ann
A det A
27. Свойства определителя матрицы
СВОЙСТВА ОПРЕДЕЛИТЕЛЯМАТРИЦЫ
28.
29.
30. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ МАТРИЦ 1-го и 2-го ПОРЯДКОВ
ВЫЧИСЛЕНИЕОПРЕДЕЛИТЕЛЕЙ МАТРИЦ
1-ГО И 2-ГО ПОРЯДКОВ
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 1-го ПОРЯДКА
a11 a11
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2-го ПОРЯДКА
a11
a12
a21 a22
a11 a22 a21 a12
31. МНЕМОНИЧЕСКОЕ ПРАВИЛО
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ2-го ПОРЯДКА РАВЕН
ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ
ГЛАВНОЙ ДИАГОНАЛИ
МИНУС
ПРОИЗВЕДЕНИЕ ЭЛЕМЕНТОВ
ПОБОЧНОЙ ДИАГОНАЛИ
32. Определитель матрицы «три на три» 1-й способ
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ «ТРИ НА ТРИ»1-Й СПОСОБ
33.
34. Определитель матрицы «три на три» 2-й способ способ Саррюса или способ «параллельных полосок»
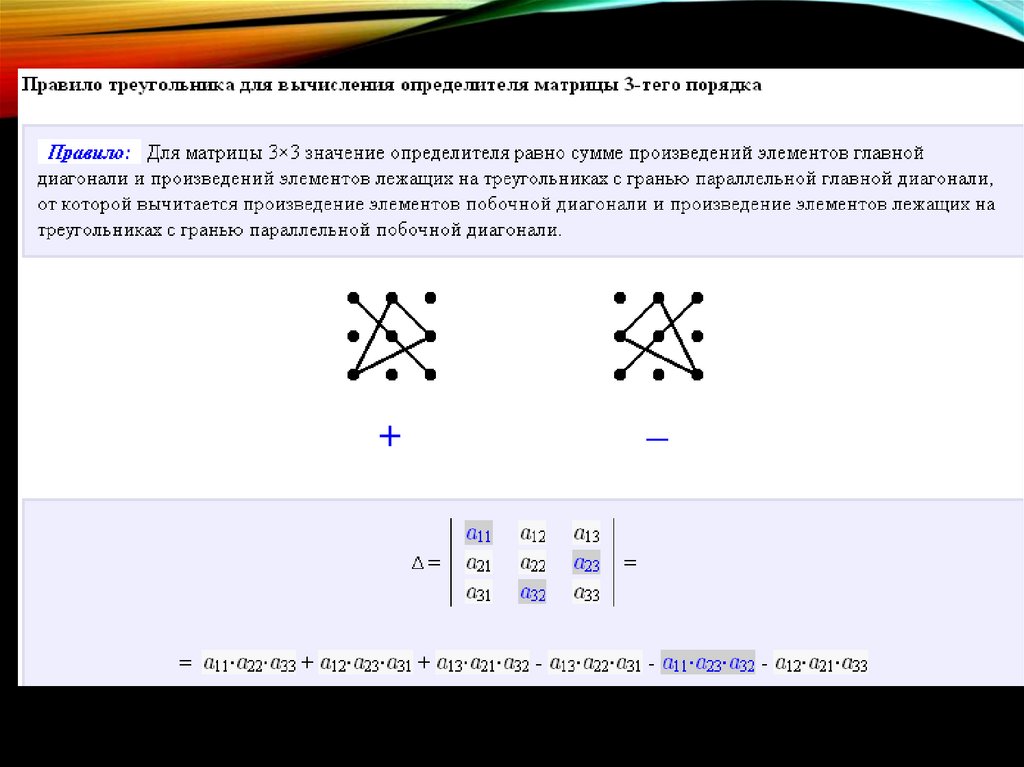
ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ «ТРИ НА ТРИ»2-Й СПОСОБ
СПОСОБ САРРЮСА ИЛИ СПОСОБ «ПАРАЛЛЕЛЬНЫХ
ПОЛОСОК»
35. МИНОРЫ И АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
36. МИНОР ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯ
МИНОРОМ ЭЛЕМЕНТА ОПРЕДЕЛИТЕЛЯНАЗЫВАЕТСЯ ОПРЕДЕЛИТЕЛЬ,
ПОЛУЧЕННЫЙ ИЗ ИСХОДНОГО
ОПРЕДЕЛИТЕЛЯ ПРИ ПОМОЩИ
ВЫЧЕРКИВАНИЯ СТРОКИ И
СТОЛБЦА, В КОТОРЫХ
СТОИТ ЭТОТ ЭЛЕМЕНТ
37. ПРИМЕР ВЫЧИСЛЕНИЯ МИНОРА
МИНОР M 21 ЭЛЕМЕНТА a21 ОПРЕДЕЛИТЕЛЯ3 1 2
4
2 0
7
9 1
ВЫЧИСЛЯЕТСЯ ТАК:
1 2
M 21
9 1
1 2
9
1
1 18 19
38. АЛГЕБРАИЧЕСКОЕ ДОПОЛНЕНИЕ
АЛГЕБРАИЧЕСКИМ ДОПОЛНЕНИЕМ AijЭЛЕМЕНТА aij ОПРЕДЕЛИТЕЛЯ
НАЗЫВАЕТСЯ ЧИСЛО
Aij ( 1)i j M ij ,
ГДЕ M ij МИНОР ЭЛЕМЕНТА aij
39. СПОСОБЫ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЕЙ
40. РАЗЛОЖЕНИЕ ПО ЛЮБОЙ СТРОКЕ (ЛЮБОМУ СТОЛБЦУ)
ОПРЕДЕЛИТЕЛЬРАВЕН СУММЕ ПРОИЗВЕДЕНИЙ
ЭЛЕМЕНТОВ ЛЮБОЙ СТРОКИ
(ЛЮБОГО СТОЛБЦА) НА ИХ
АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ
41. ПРИМЕР ВЫЧИСЛЕНИЯ ОПРЕДЕЛИТЕЛЯ
42. МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯ ВЫЧИСЛЕНИЯ ОПРЕДЕЛИ-ТЕЛЕЙ МАТРИЦ 3-го ПОРЯДКА
МЕТОД ТРЕУГОЛЬНИКОВ ДЛЯВЫЧИСЛЕНИЯ ОПРЕДЕЛИ-ТЕЛЕЙ
МАТРИЦ 3-ГО ПОРЯДКА
a12
a33 a31
a22
a
31
a13
a21
a12
a11
a22
a23 a21
a11
a33
a32
a32
a13
a23
43. ПРИМЕР ИСПОЛЬЗОВАНИЯ МЕТОДА ТРЕУГОЛЬНИКОВ
23
5
1 3
3
2
4
1
2 1 1 3 ( 3) ( 3) 5 ( 2) 4
4 1 ( 3) 5 3 1 ( 2) ( 3) 2
2 27 40 12 15 12 26
44. ОПРЕДЕЛИТЕЛЬ ТРЕУГОЛЬНОЙ МАТРИЦЫ РАВЕН ПРОИЗВЕДЕНИЮ ЭЛЕМЕНТОВ ГЛАВНОЙ ДИАГОНАЛИ
3 1 20
0
2 0 3 2 1 6
0 1
45. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
46. ОБЩИЙ ВИД СИСТЕМЫ n ЛИНЕЙНЫХ УРАВНЕНИЙ С n НЕИЗВЕСТНЫМИ
ОБЩИЙ ВИД СИСТЕМЫ NЛИНЕЙНЫХ УРАВНЕНИЙ С
N НЕИЗВЕСТНЫМИ
47. МАТРИЧНЫЙ ВИД СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
a11 a12a
a22
21
... ...
a
n1 an 2
... a1n x1 b1
... a2 n x2 b2
... ... ... ...
... ann xn bn
48. ГЛАВНЫЙ ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
a11a12
... a1n
a21
a22
... a2 n
...
...
...
...
an1 an 2 ... ann
49. ПРИМЕНЕНИЕ МЕТОДА КРАМЕРА НА ПРИМЕРЕ СИСТЕМЫ ИЗ 3-х УРАВНЕНИЙ
ПРИМЕНЕНИЕ МЕТОДАКРАМЕРА НА ПРИМЕРЕ
СИСТЕМЫ ИЗ 3-Х
УРАВНЕНИЙ
a11 a12
a
a22
21
a
31 a32
a13 x1 b1
a23 x2 b2
a33 x3 b3
50. НЕОБХОДИМОЕ УСЛОВИЕ ПРИМЕНИМОСТИ ФОРМУЛ КРАМЕРА
a11a12
a21 a22
a31
a32
a13
a23 0
a33
51. ВЫЧИСЛЕНИЕ ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ
b1a12
a13
a11
b1
a13
1 b2
a22
a23 ;
2 a21 b2
a23
b3
a32
a33
a31
a33
a11
a12
b1
3 a21 a22
b2
a31
b3
a32
b3
52. ФОРМУЛЫ КРАМЕРА ДЛЯ РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
1x1 ,
2
x2
,
3
x3
53. ПРИМЕР РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ КРАМЕРА
2 x y 3z 13,4 x 3 y z 7,
x 2 y 5 z 15
54. ВЫЧИСЛЕНИЕ ГЛАВНОГО И ДОПОЛНИТЕЛЬНЫХ ОПРЕДЕЛИТЕЛЕЙ
24
1
1
ВЫЧИСЛЕНИЕ ГЛАВНОГО И
ДОПОЛНИТЕЛЬНЫХ
ОПРЕДЕЛИТЕЛЕЙ
3
3 1 30 24 1 9 4 20 14 0,
2
5
13 1
1 7
3
15 2
3
1 195 42 15 135 26 35 42,
5
55. ПРОДОЛЖЕНИЕ ВЫЧИСЛЕНИЙ ОПРЕДЕЛИТЕЛЕЙ
2 132 4
7
1 15
3
1 70 130 13 21 30 260 14,
5
2 1 13
3 4
3
7 90 140 7 39 28 60 28.
1 2 15
56. ОКОНЧАТЕЛЬНЫЙ ОТВЕТ
1 42x
3,
14
2 14
y
1,
14
3 28
z
2.
14
57. Обратная матрица
ОБРАТНАЯ МАТРИЦАМатрица А-1 называется обратной по отношению к
квадратной матрице А, если при умножении этой
матрицы на обратную, как справа, так и слева
получается единичная матрица:
А-1 * А = А * А-1 = Е
Из определения следует, что только квадратная
матрица имеет обратную; при этом обратная
матрица также является квадратной того же
порядка. Однако не каждая квадратная матрица
имеет обратную.
Теорема (необходимое и достаточное условие существования
обратной матрицы). Обратная матрица существует (и единственна)
тогда и только тогда, когда исходная матрица невырожденная |A-1| ≠0.






























































 Математика
Математика








