Длина окружности

1. Длина окружности

Длиной окружности считают число, к которому
стремятся периметры вписанных в эту окружность
правильных многоугольников при увеличении числа их
сторон.
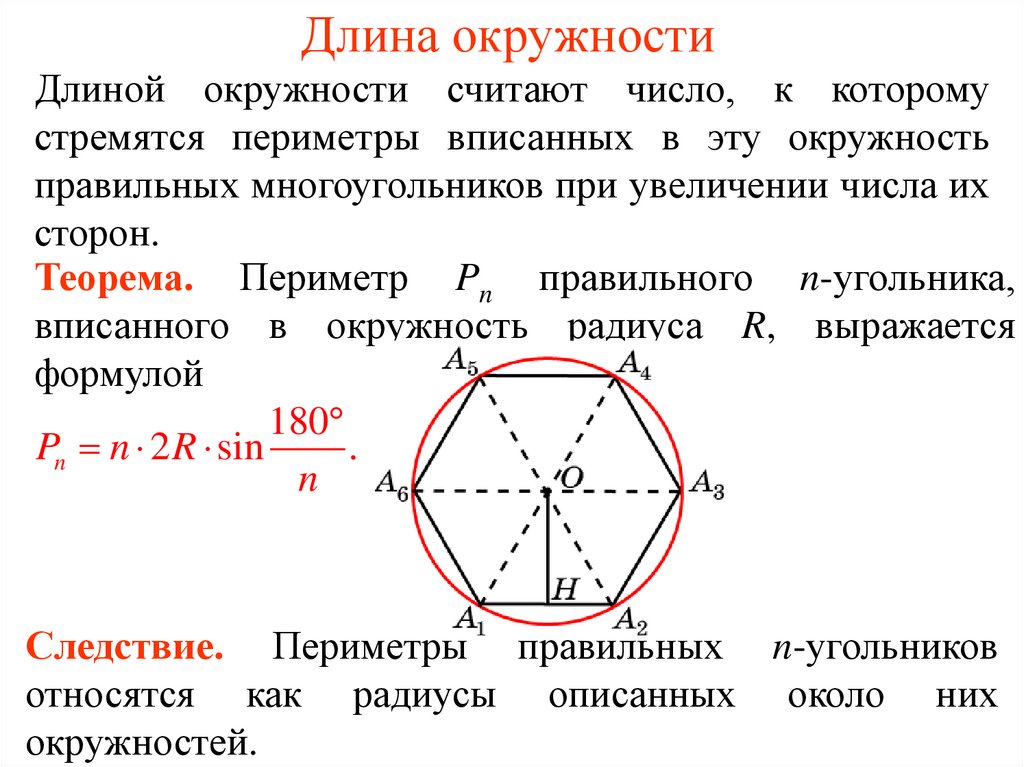
Теорема. Периметр Pn правильного n-угольника,
вписанного в окружность радиуса R, выражается
формулой
180
Pn n 2 R sin
.
n
Следствие. Периметры правильных n-угольников
относятся как радиусы описанных около них
окружностей.

2. Длина окружности

Теорема. Отношение длин двух окружностей равно
отношению их радиусов.
Половина длины окружности единичного радиуса
обозначается греческой буквой π. Таким образом, длина
окружности единичного радиуса равна 2π. Длина
окружности радиуса R равна 2πR. Таким образом, для
длины окружности C радиуса R можем записать
следующую формулу: C = 2πR.

3. Приближенное вычисление числа π

Для приближенного вычисления числа π в единичную
окружность вписывают правильный многоугольник и
находят его полупериметр. Чем больше число сторон
вписанного многоугольника, тем более точное значение
получается для числа π.
Первое вычисление числа π, использующее строгие
рассуждения, было сделано величайшим математиком
древности Архимедом (287 - 212 гг. до н. э.). В своей
работе "Об измерении круга" он доказал, что для числа
π выполняются неравенства 3 10 3 1 .
71
7
На практике приближенное значение числа π берется
равным 3,14.

4. Измерение длины дуги окружности

Центральные углы в 1о разбивают всю окружность на
360 равных секторов. Поэтому длина дуги окружности в
1
о
1 составляет
часть длины всей окружности, т.е. равна
360
2 R R
360 180 . Длина l дуги окружности радиуса R в φ
градусов будет выражаться формулой
R
l
.
180

5. Измерение угла окружности

Равенство l
, выражающее длину дуги единичной
180
окружности, устанавливает соответствие между длиной
дуги и ее градусной мерой.
Это позволяет измерять углы не только с помощью
градусов, но и с помощью длины дуги соответствующей
окружности единичного радиуса. Величина длины дуги
называется радианной мерой угла. Единицей радианной
меры углов является радиан. Угол в один радиан – это
угол, для которого длина соответствующей дуги
единичной окружности равна единице.
180
57 .
Градусная мера угла в один радиан равна

6. Вопрос 1

Как относятся периметры двух правильных nугольников?
Ответ. Периметры правильных n-угольников относятся
как радиусы описанных около них окружностей.

7. Вопрос 2

Как относятся длины двух окружностей?
Ответ. Отношение длин двух окружностей равно
отношению их радиусов.

8. Вопрос 3

Что обозначает греческая буква π?
Ответ. Греческая буквой π обозначает половину длины
окружности единичного радиуса.

9. Вопрос 4

Чему равна длина окружности радиуса R?
Ответ. Длина окружности радиуса R равна 2πR.

10. Вопрос 5

Какие неравенства выполняются для числа π?
Ответ. Для числа π выполняются неравенства
10
1
3 3 .
71
7

11. Вопрос 6

Каково приближенное значение числа π?
Ответ. Приближенное значение числа π берется равным
3,14.

12. Вопрос 7

Чему равна длина дуги окружности в 1о?
Ответ. Длина дуги окружности в
1о
равна
R
.
180

13. Вопрос 8

Чему равна длина дуги окружности в φ
градусов?
Ответ. Длина l дуги окружности радиуса R в φ градусов
будет выражаться формулой
R
l
.
180

14. Вопрос 9

Чему равна градусная мера угла в один радиан?
Ответ. Градусная мера угла в один радиан равна
180
57 .

15. Пример

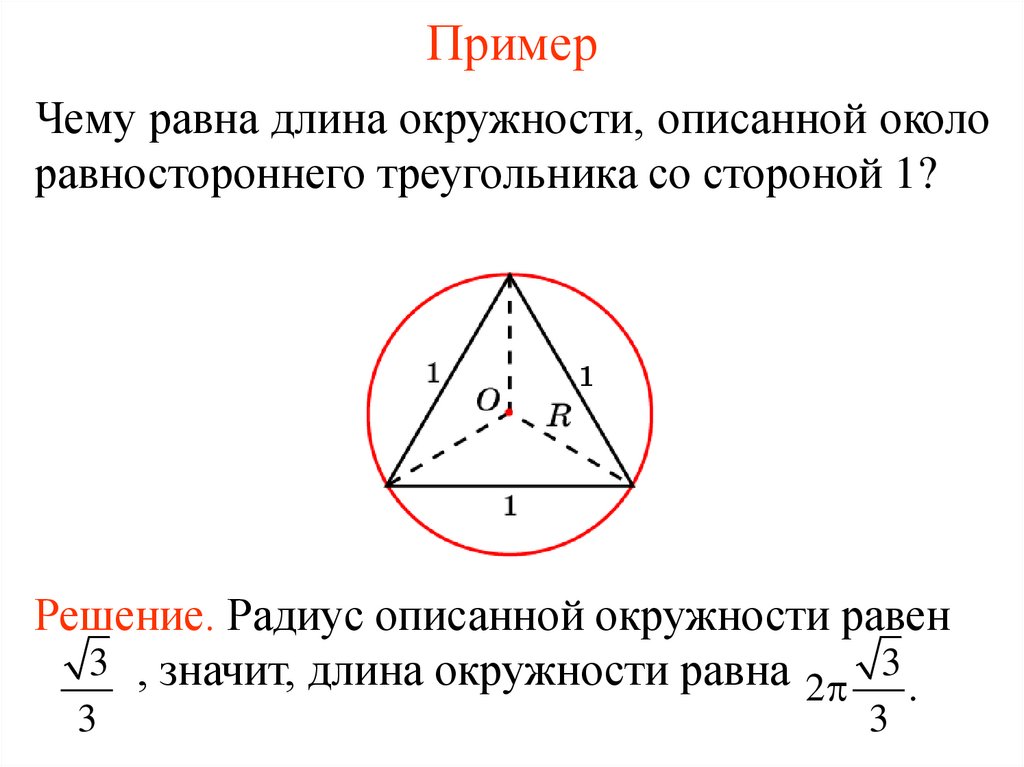
Чему равна длина окружности, описанной около
равностороннего треугольника со стороной 1?
Решение. Радиус описанной окружности равен
3 , значит, длина окружности равна
3
2
.
3
3

16. Упражнение 1

Как изменится длина окружности, если радиус
окружности: а) увеличить в три раза; б)
уменьшить в два раза?

17. Упражнение 2

Найдите длину окружности, описанной около
квадрата со стороной а?

18. Упражнение 3

Найдите длину дуги окружности радиуса
единица, соответствующей центральному углу в:
а) 30о; б) 135о; в) 240о; г) 315о.

19. Упражнение 4

Каким должен быть радиус окружности, в которой
дуга в 1о имеет длину 1 см? Укажите
приближенное значение, равное целому числу
сантиметров.

20. Упражнение 7

Найдите радианную меру углов в: а) 30о; б)
45о; в) 60о.

21. Упражнение 8

Найдите градусную меру угла, если его
5
радианная мера равна: а)
; б) ; в) ; г) ;
8
4
6
2
д) 7 ; е) 4 .
18
3