Теорема о медиане треугольника

1.

Теорема о медиане
треугольника
Методическая разработка
учителя Поляковой Е. А.

2.

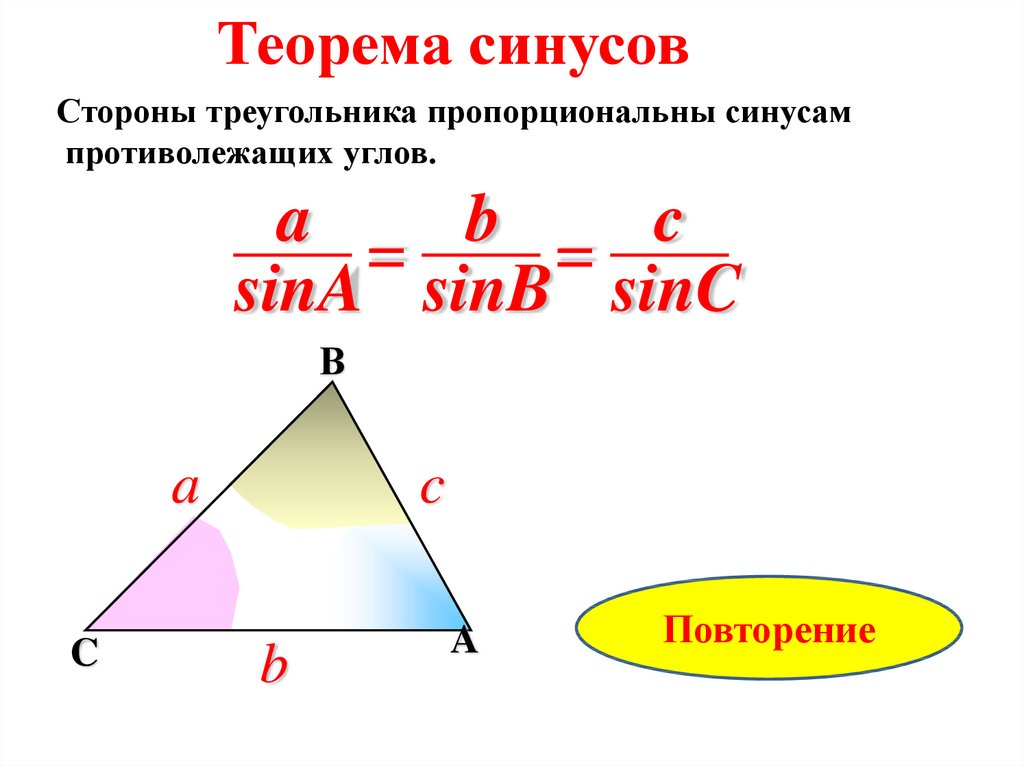
Теорема синусов
Стороны треугольника пропорциональны синусам
противолежащих углов.
a = b = c
sinA sinB sinC
В
a
C
c
b
A
Повторение

3.

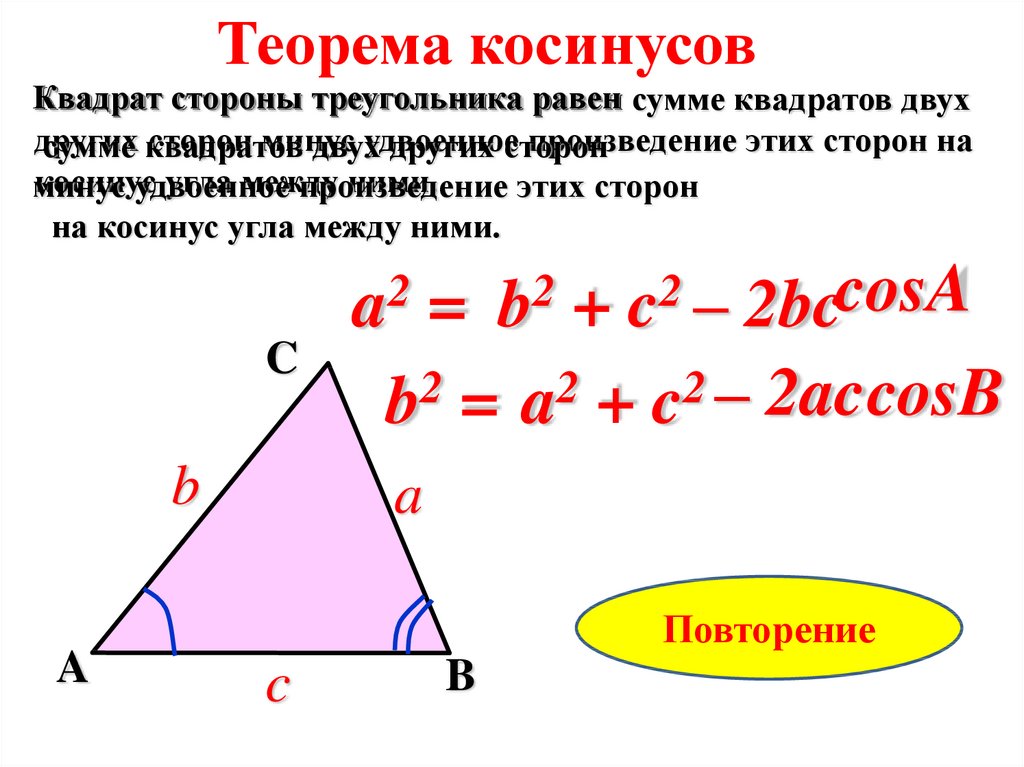
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух
других
сторон минус
удвоенное
произведение этих сторон на
сумме квадратов
двух
других сторон
косинус
угла между
ними.
минус
удвоенное
произведение
этих сторон
на косинус угла между ними.
=
+
2bccosA
2
2
2
b = a + c – 2accosB
2
a
C
b
A
2
b
2
c –
a
Повторение
c
B

4.

Косинус угла треугольника
b a c 2ac cos B
2
2
2
2ac cos B a c b : 2aс
2
2
2
а с b
cos В
2ac
2
2
2
Повторение

5.

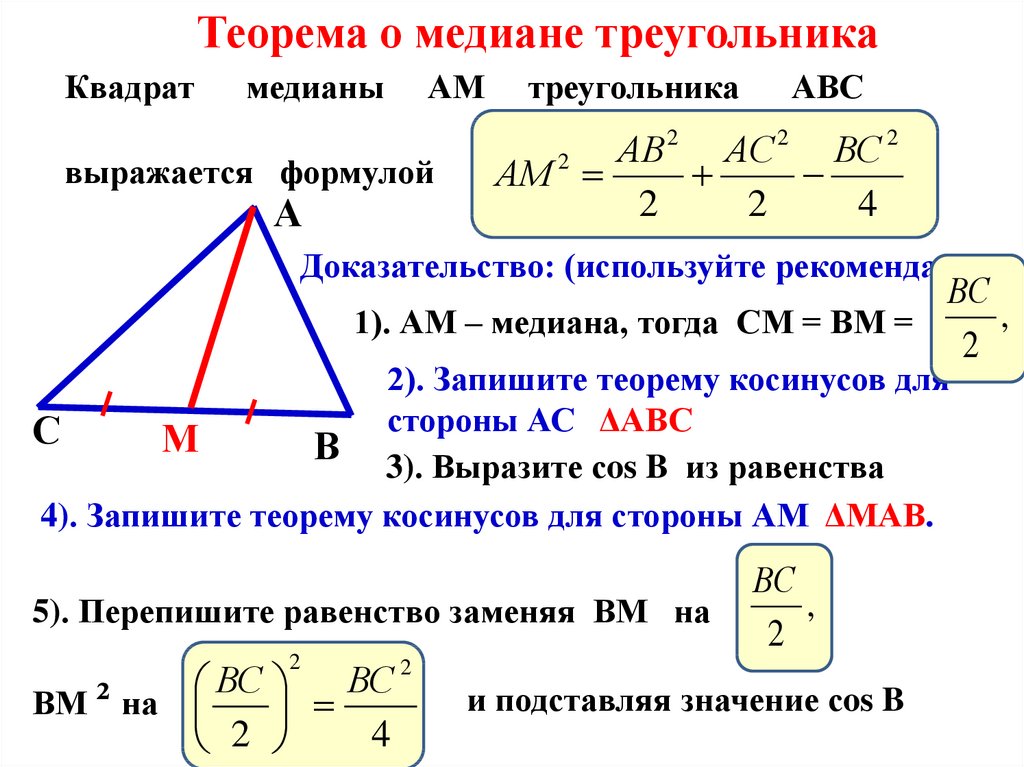
Теорема о медиане треугольника
Квадрат
медианы
АМ
выражается формулой
А
треугольника
АВС
2
2
2
АВ
АС
ВС
АМ 2
2
2
4
Доказательство: (используйте рекомендации)
ВС
,
1). АМ – медиана, тогда СМ = ВМ =
2
2). Запишите теорему косинусов для
стороны АС ΔАВС
С
М
В 3). Выразите сos B из равенства
4). Запишите теорему косинусов для стороны АМ ΔМАВ.
5). Перепишите равенство заменяя ВМ на
2
2
ВС
ВС
ВМ ² на
4
2
ВС
,
2
и подставляя значение сos B

6.

Теорему о медиане треугольника
можно сформулировать так:
Квадрат медианы треугольника,
проведённой из какой- либо его вершины,
равен полусумме квадратов двух его сторон,
проведённых из этой же вершины,
минус четверть квадрата третьей стороны

7.

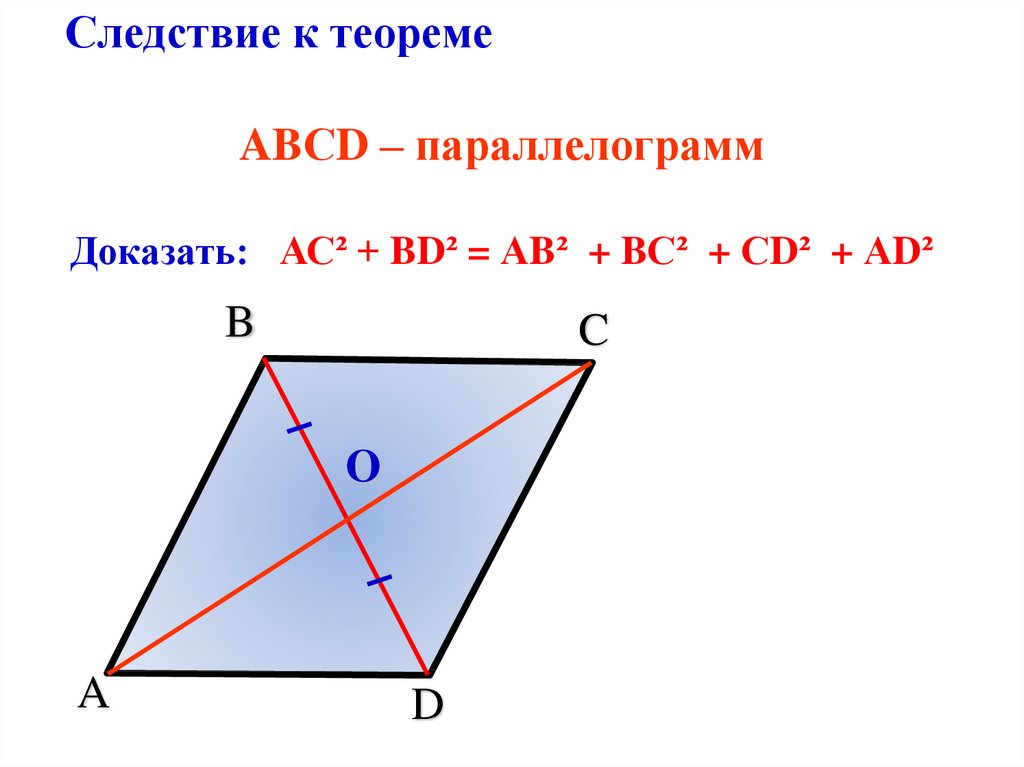
Следствие к теореме
ABСD – параллелограмм
Доказать: АС² + BD² = АB² + BС² + СD² + АD²
B
C
O
A
D

8.

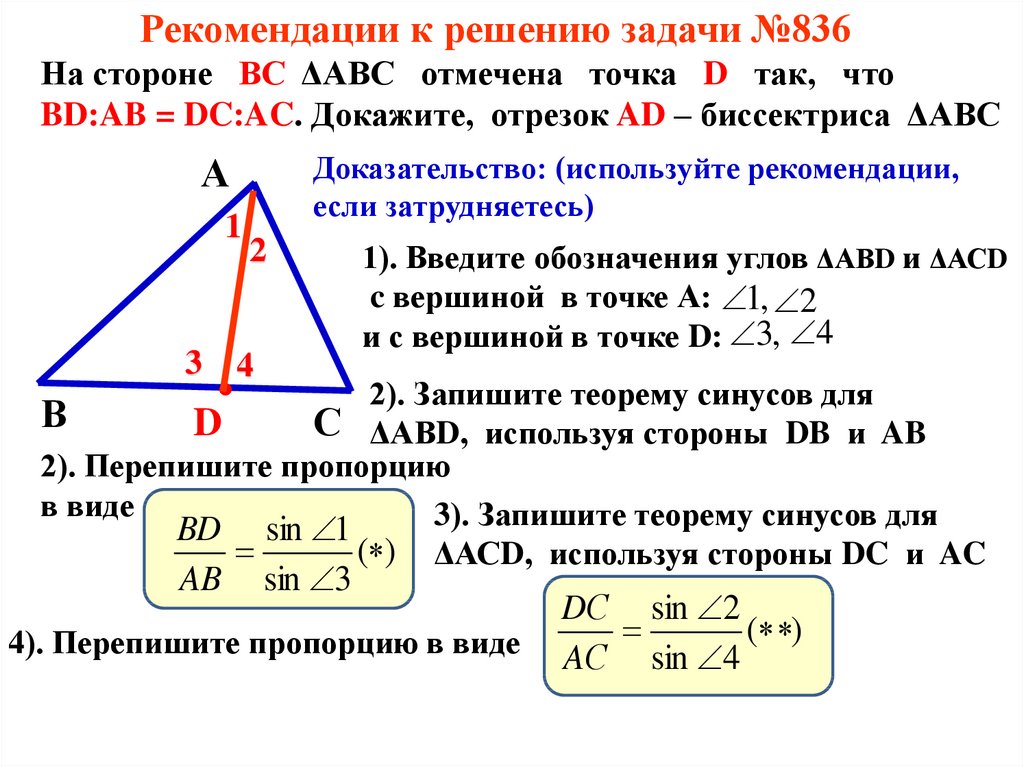
Рекомендации к решению задачи №836
На стороне ВС ΔАВС отмечена точка D так, что
BD:AB = DC:AC. Докажите, отрезок AD – биссектриса ΔАВС
Доказательство: (используйте рекомендации,
если затрудняетесь)
А
1
3
2
4
1). Введите обозначения углов ΔАВD и ΔАСD
c вершиной в точке А: 1, 2
и с вершиной в точке D: 3, 4
2). Запишите теорему синусов для
В
D
С ΔАВD, используя стороны DB и AB
2). Перепишите пропорцию
в виде
3). Запишите теорему синусов для
BD sin 1
( ) ΔАСD, используя стороны DC и AC
AB
sin 3
4). Перепишите пропорцию в виде
DС sin 2
( )
AС sin 4

9.

5). Завершите предложение - углы 3 и 4 являются …
6). Воспользуйтесь свойством синусов смежных углов
7). Перепишите пропорцию (**), заменяя sin 4
8). Пропорцию BD:AB = DC:AC из условия задачи перепишите
в виде
BD DC
(* * *)
AB AC
9). Перепишите пропорцию (***), используя шаги 2) и 7)
10). Сделайте заключение об углах 1 и 2 и об отрезке AD