Теорема о биссектрисе треугольника

1.

Теорема о биссектрисе
треугольника
Методическая разработка
учителя Поляковой Е. А.

2.

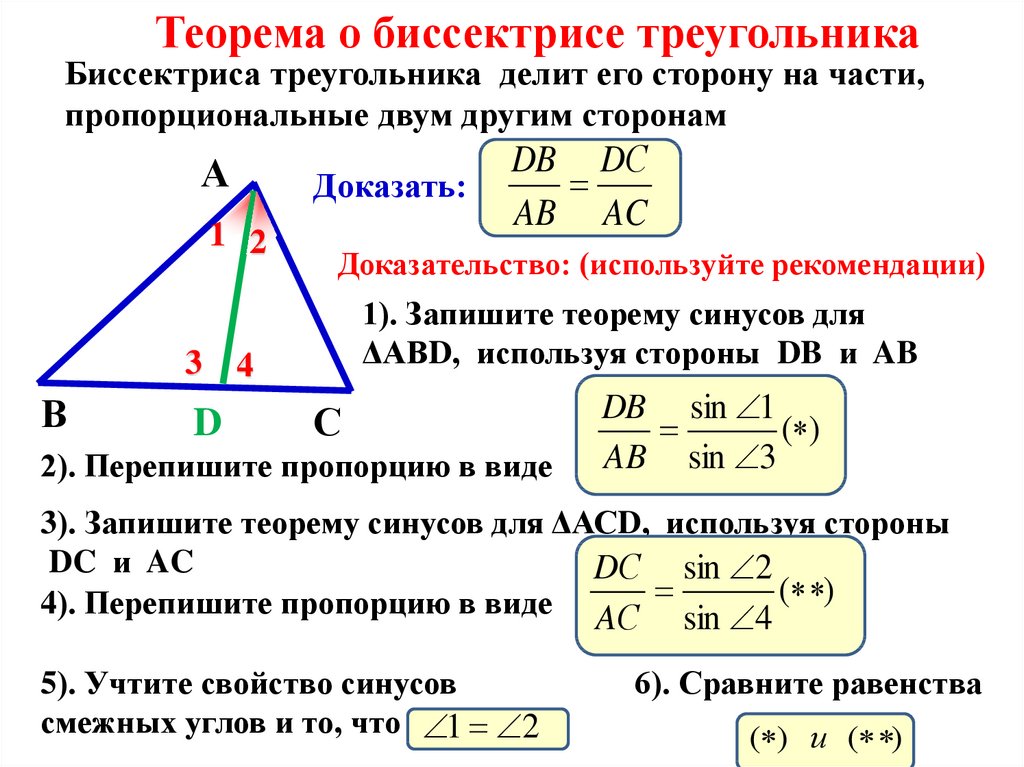
Теорема о биссектрисе треугольника
Биссектриса треугольника делит его сторону на части,
пропорциональные двум другим сторонам
А
Доказать:
1 2
3
В
D
DB DС
AB AC
Доказательство: (используйте рекомендации)
1). Запишите теорему синусов для
ΔАВD, используя стороны DB и AB
4
С
2). Перепишите пропорцию в виде
DB sin 1
( )
AB sin 3
3). Запишите теорему синусов для ΔАСD, используя стороны
DC и AC
DС sin 2
4). Перепишите пропорцию в виде AС sin 4 ( )
5). Учтите свойство синусов
смежных углов и то, что 1 2
6). Сравните равенства
( ) и ( )

3.

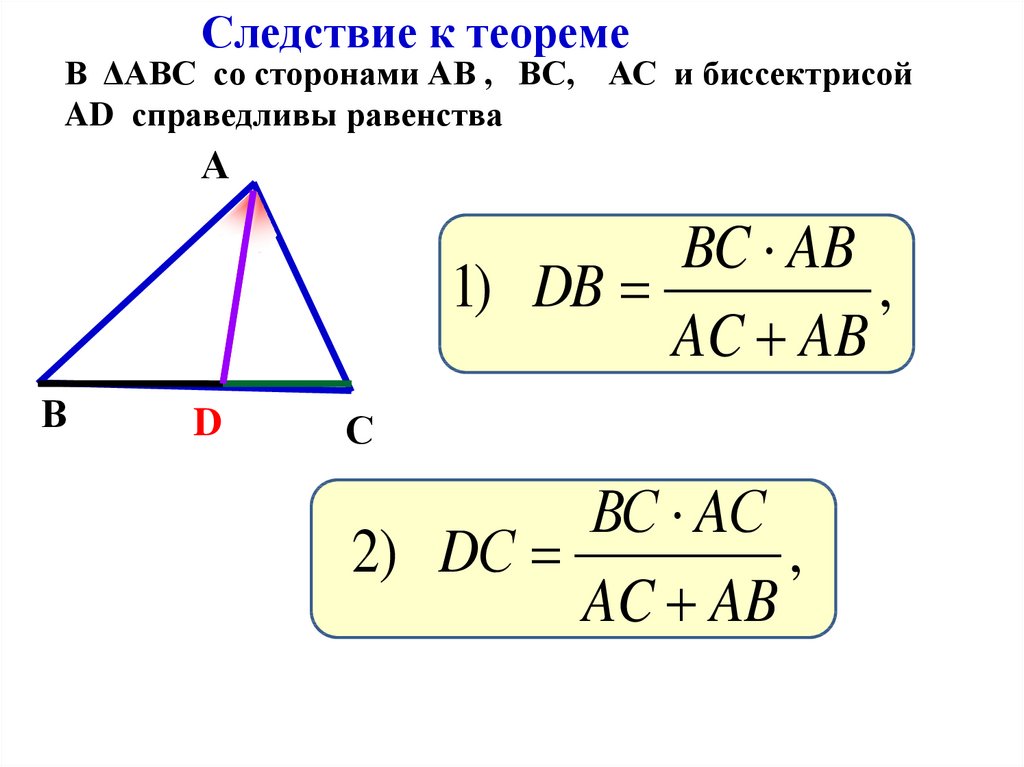
Следствие к теореме
В ΔАВС со сторонами АВ , ВС,
AD справедливы равенства
АС и биссектрисой
А
BC AB
1) DB
,
AC AB
В
D
С
ВС AС
2) DС
,
AC AB

4.

Следующее утверждение связывает
биссектрису AD со сторонами ΔАВС
AD AB AC DB DC
2
Квадрат биссектрисы треугольника,
проведённой из какой- либо его вершины,
равен произведению двух его сторон,
проведённых из этой же вершины,
минус произведение отрезков третьей стороны

5.

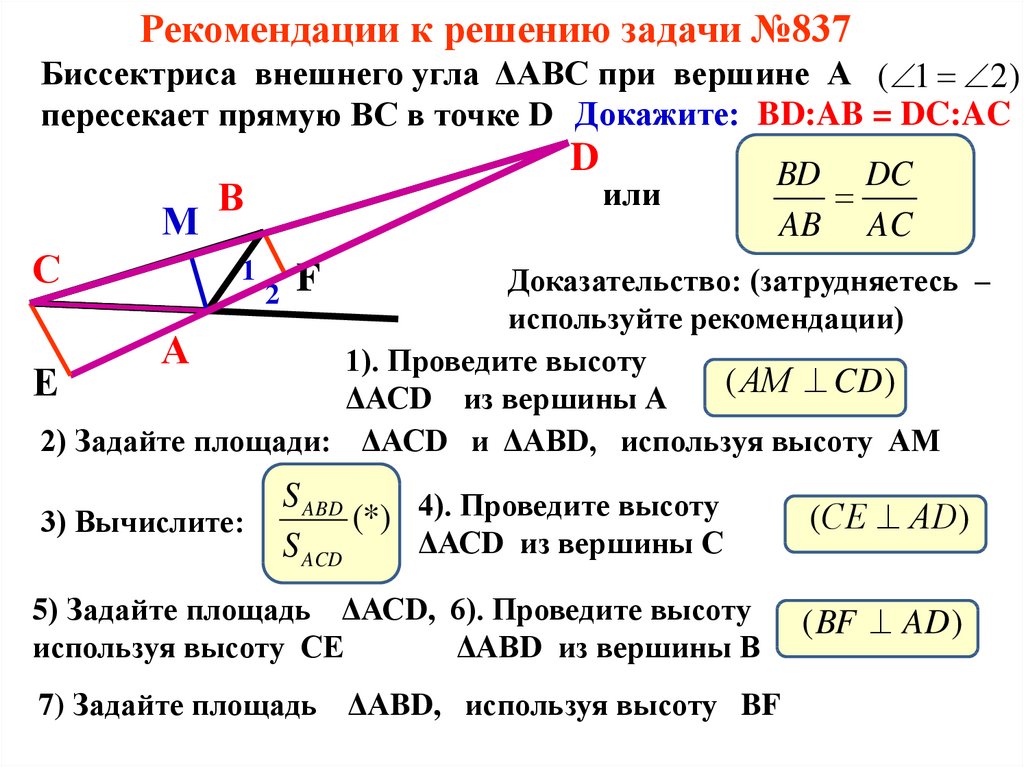
Рекомендации к решению задачи №837
Биссектриса внешнего угла ΔАВС при вершине А ( 1 2 )
пересекает прямую ВС в точке D Докажите: BD:AB = DC:AC
М
С
D
В
1
или
BD DC
AB AC
Доказательство: (затрудняетесь –
используйте рекомендации)
А
1). Проведите высоту
( АМ CD )
Е
ΔАСD из вершины А
2) Задайте площади: ΔАСD и ΔАВD, используя высоту АМ
3) Вычислите:
2
F
S ABD
(*) 4). Проведите высоту
ΔАСD из вершины С
S ACD
5) Задайте площадь ΔАСD, 6). Проведите высоту
используя высоту СЕ
ΔАВD из вершины В
7) Задайте площадь ΔАBD, используя высоту BF
(СЕ АD )
( BF AD )

6.

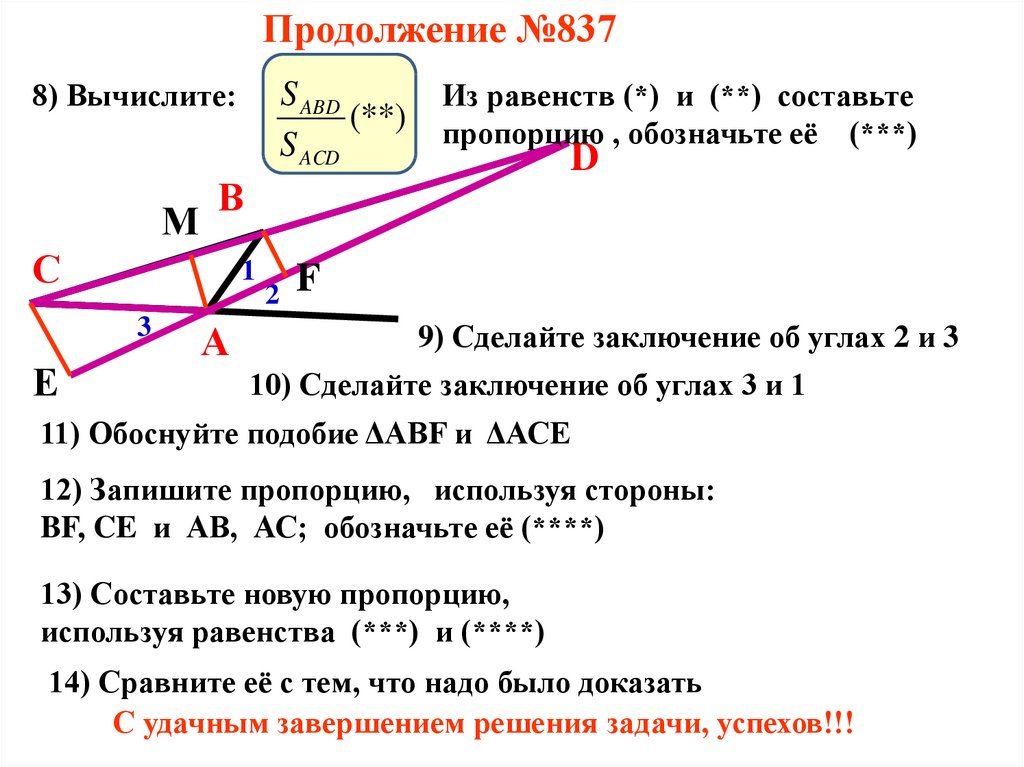
Продолжение №837
8) Вычислите:
М
В
С
1
3
Е
S ABD
Из равенств (*) и (**) составьте
(**) пропорцию , обозначьте её (***)
S ACD
D
А
2
F
9) Сделайте заключение об углах 2 и 3
10) Сделайте заключение об углах 3 и 1
11) Обоснуйте подобие ΔАВF и ΔАСЕ
12) Запишите пропорцию, используя стороны:
BF, CE и АВ, АС; обозначьте её (****)
13) Составьте новую пропорцию,
используя равенства (***) и (****)
14) Сравните её с тем, что надо было доказать
С удачным завершением решения задачи, успехов!!!

7.

Письменный опрос следующего
урока, проверяющий усвоение
теории, может включать следующие
задания:

8.

1. Изобразите треугольник;
обозначьте его вершины;
(для каждого варианта названия вершин даст
учитель);
запишите для него теорему синусов
2. Запишите теорему косинусов для какой – то
стороны треугольника
3. Запишите выражения для косинуса какого-то
угла треугольника
4. Проведите какую-то медиану, запишите
равенство по теореме о медиане треугольника
5. Проведите какую-то биссектрису, запишите для
неё равенство по теореме о биссектрисе
6. Запишите равенство для квадрата биссектрисы