Прямоугольные треугольники

1. .

ПРЯМОУГОЛЬНЫЙ
ТРЕУГОЛЬНИК
.

2. ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК-

ПРЯМОУГОЛЬНЫЙ
ТРЕУГОЛЬНИКЭТО ТРЕУГОЛЬНИК, В КОТОРОМ
ОДИН ИЗ УГЛОВ ПРЯМОЙ (90 )

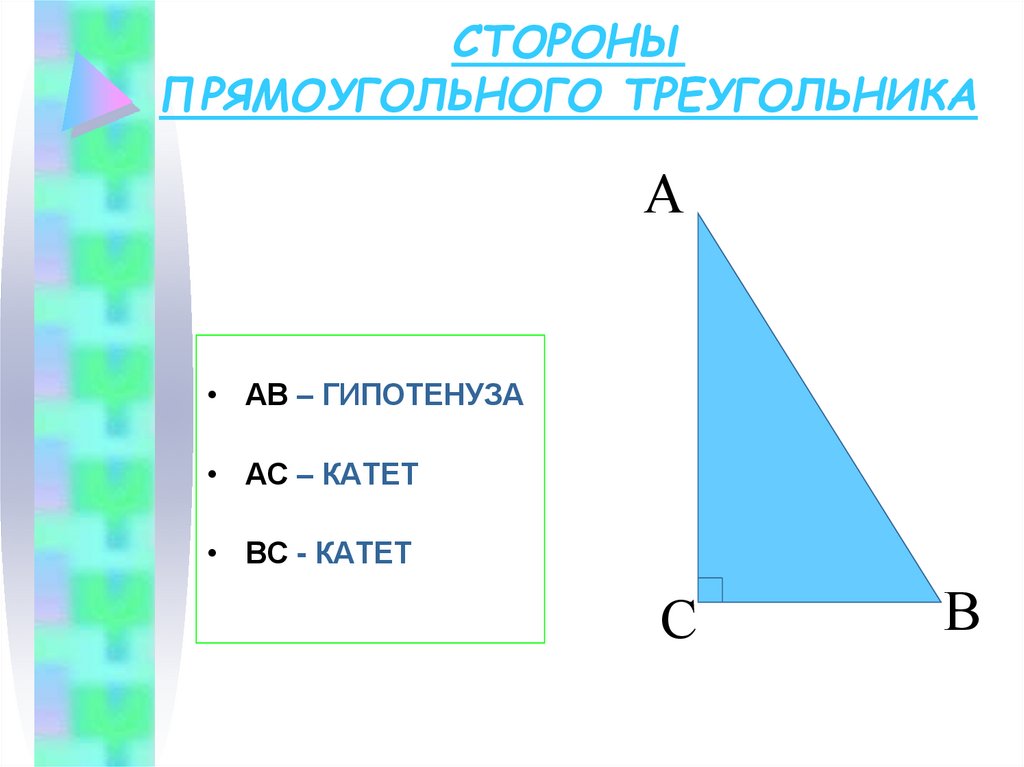
3. СТОРОНЫ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

А
• АВ – ГИПОТЕНУЗА
• АС – КАТЕТ
• ВС - КАТЕТ
С
В

4. ПРИЗНАКИ РАВЕНСТВА ПРЯМОУГОЛЬНЫХ ТРЕУГОЛЬНИКОВ

5.

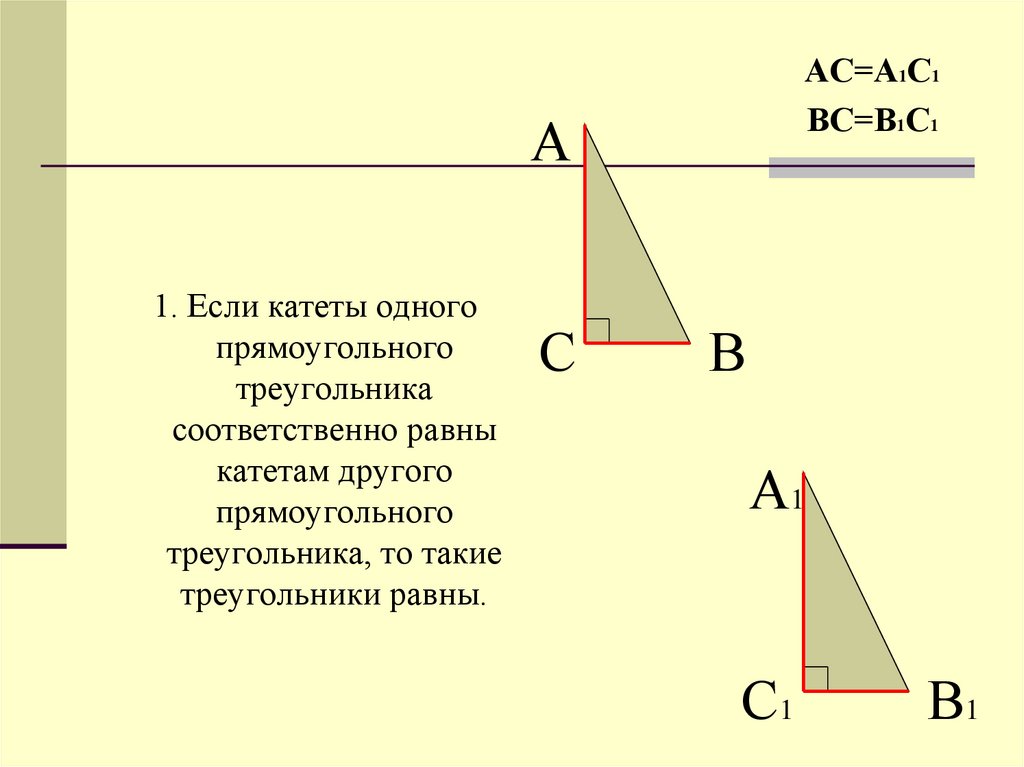
АС=А1С1
ВС=В1С1
А
1. Если катеты одного
прямоугольного
треугольника
соответственно равны
катетам другого
прямоугольного
треугольника, то такие
треугольники равны.
С
В
А1
С1
В1

6.

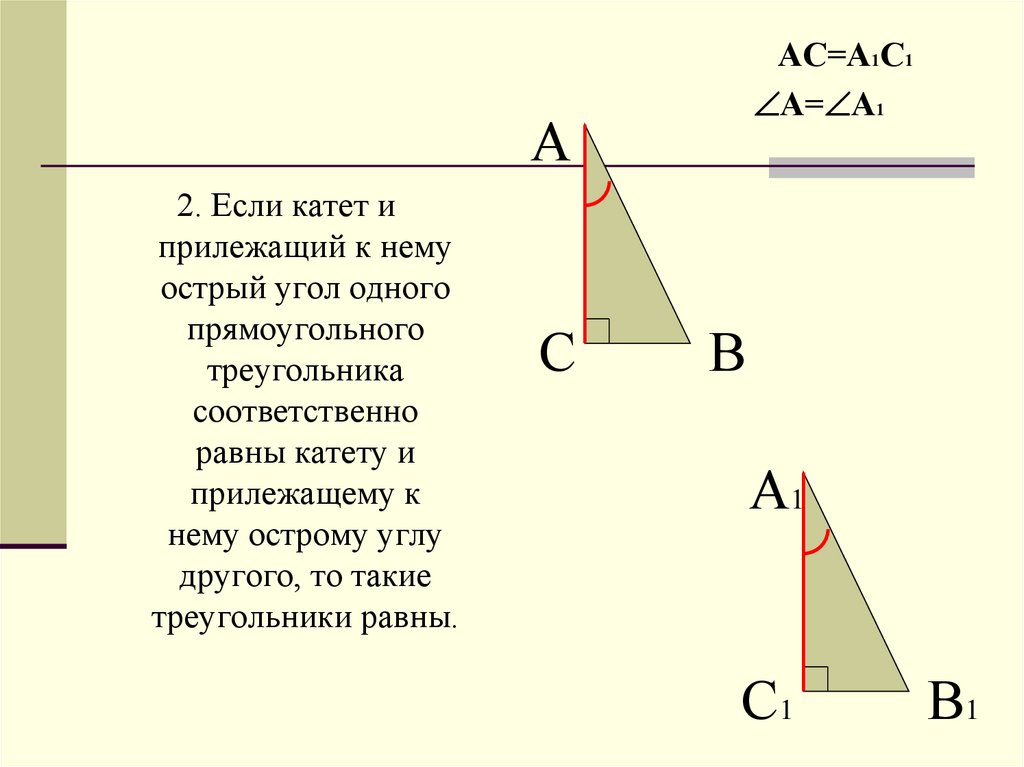
АС=А1С1
А= А1
А
2. Если катет и
прилежащий к нему
острый угол одного
прямоугольного
треугольника
соответственно
равны катету и
прилежащему к
нему острому углу
другого, то такие
треугольники равны.
С
В
А1
С1
В1

7.

АВ=А1В1
А= А1
А
3. Если гипотенуза и
острый угол
одного
прямоугольного
треугольника
соответственно
равны гипотенузе и
острому углу
другого, то такие
треугольники
равны.
С
В
А1
С1
В1

8.

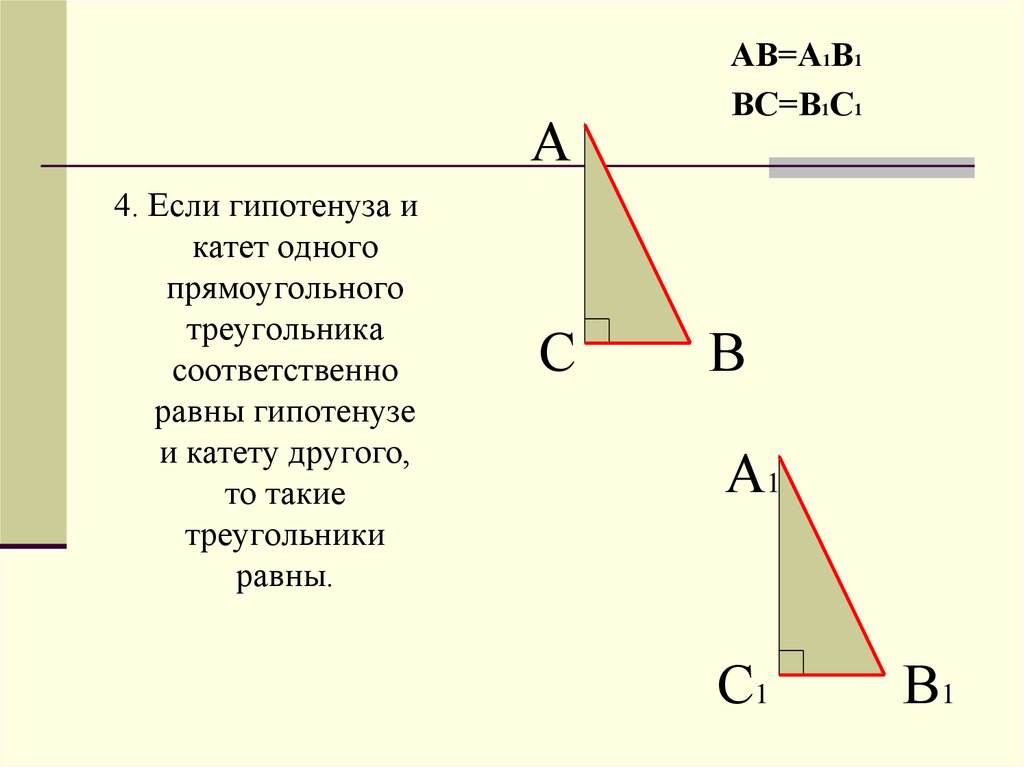
А
4. Если гипотенуза и
катет одного
прямоугольного
треугольника
соответственно
равны гипотенузе
и катету другого,
то такие
треугольники
равны.
С
АВ=А1В1
ВС=В1С1
В
А1
С1
В1

9. НЕКОТОРЫЕ СВОЙСТВА ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА

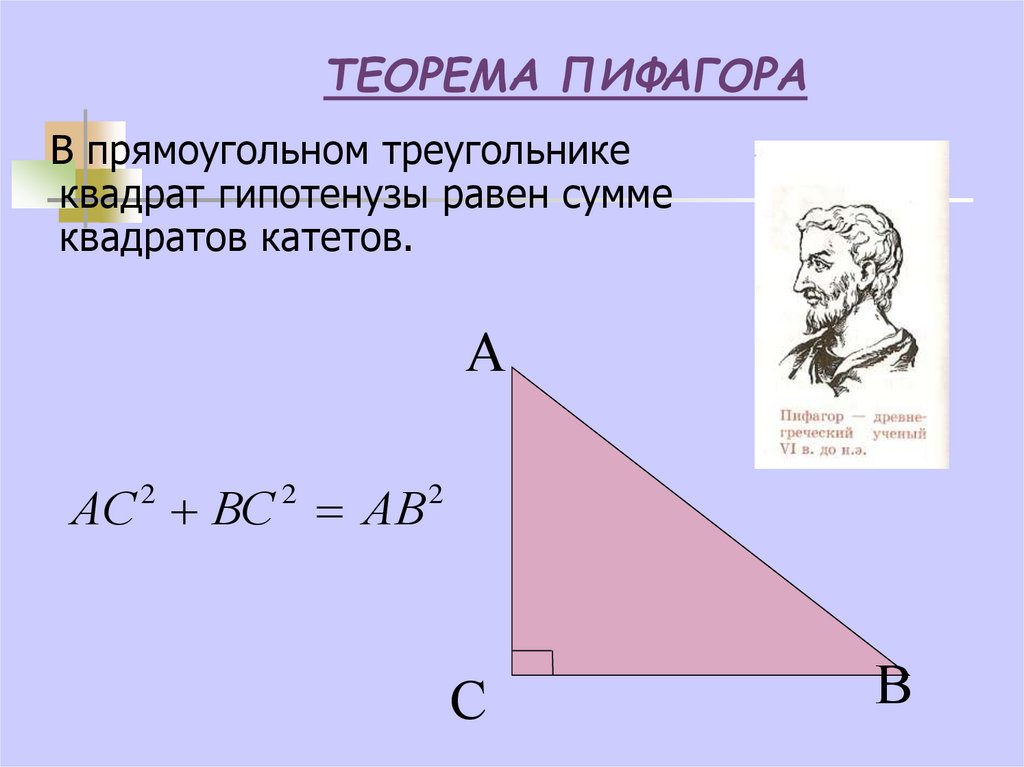
10. ТЕОРЕМА ПИФАГОРА

В прямоугольном треугольнике
квадрат гипотенузы равен сумме
квадратов катетов.
А
АС ВС АВ
2
2
2
С
В

11. Сумма острых углов прямоугольного треугольника равна 90

Сумма острых углов
прямоугольного треугольника равна 90
А
С=90
С
В
А+ В=90

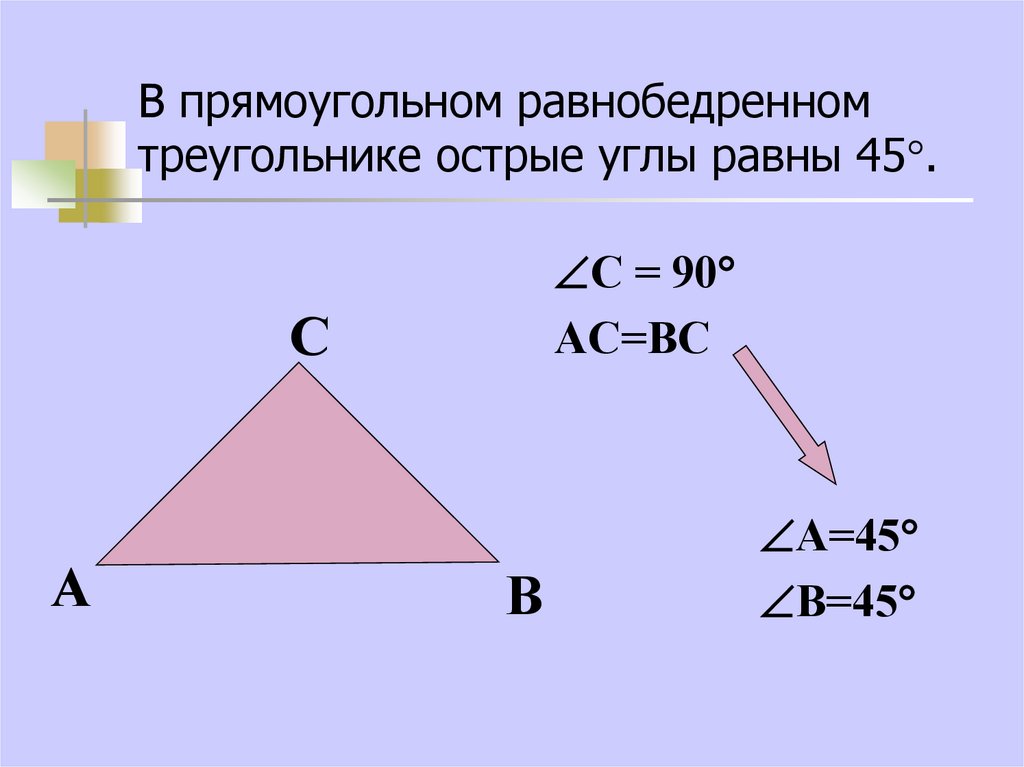
12. В прямоугольном равнобедренном треугольнике острые углы равны 45.

В прямоугольном равнобедренном
треугольнике острые углы равны 45 .
С = 90
АС=ВС
С
А
В
А=45
В=45

13.

В
Катет
прямоугольного
треугольника,
лежащий против
угла в 30 , равен
половине
гипотенузы.
В=30
АС=АВ/2
А
С

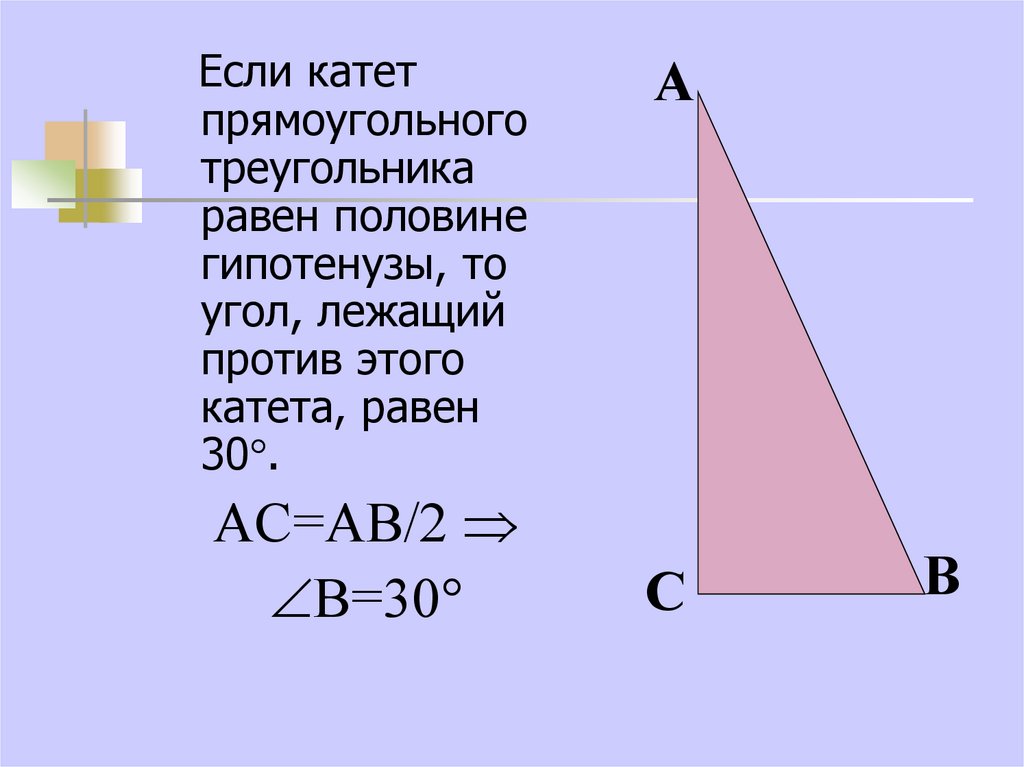
14.

Если катет
прямоугольного
треугольника
равен половине
гипотенузы, то
угол, лежащий
против этого
катета, равен
30 .
АС=АВ/2
В=30
А
С
В

15.

Высота прямоугольного
треугольника, проведённая из
вершины прямого угла, есть среднее
пропорциональное для отрезков, на
которые делится гипотенуза высотой.
А
С
Н
СН АН НВ
В

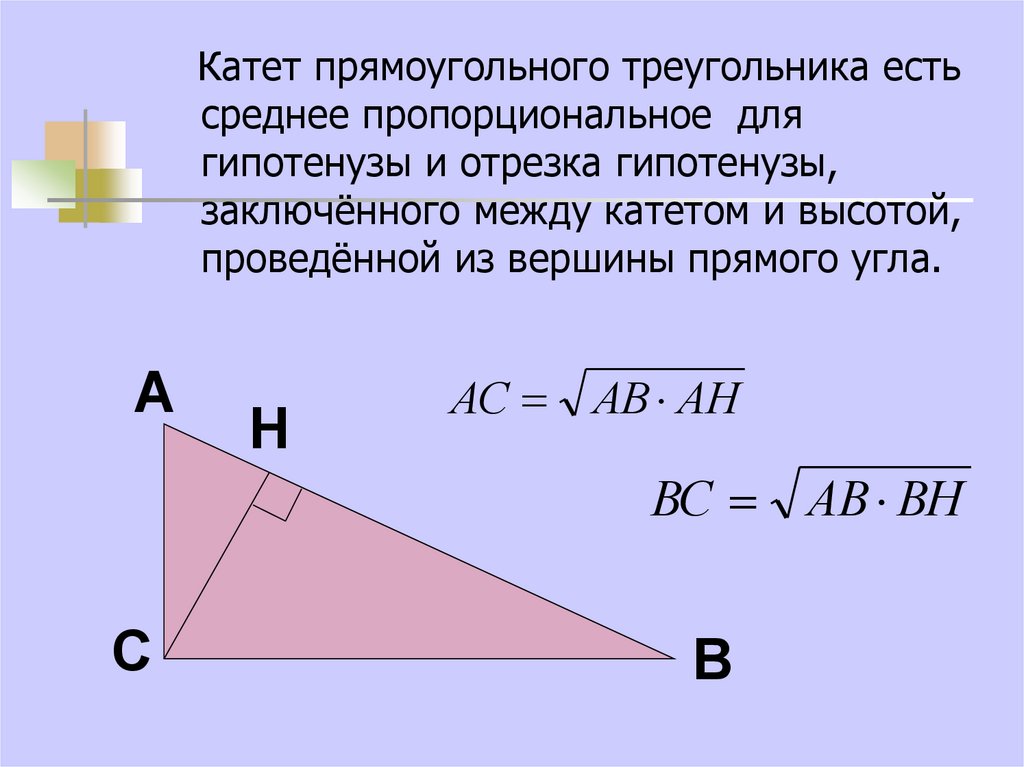
16.

Катет прямоугольного треугольника есть
среднее пропорциональное для
гипотенузы и отрезка гипотенузы,
заключённого между катетом и высотой,
проведённой из вершины прямого угла.
А
Н
АС АВ АН
ВС АВ ВН
С
В