Пирамида в задачах ЕГЭ

1. Пирамида в задачах ЕГЭ

2.

Задача 1. В правильном единичном тетраэдре
ABCD найдите расстояние от вершины A до
прямой BC.
Решение. Искомое расстояние равно высоте AH треугольника
ABC. Оно равно 3 .
2
3
.
Ответ:
2

3.

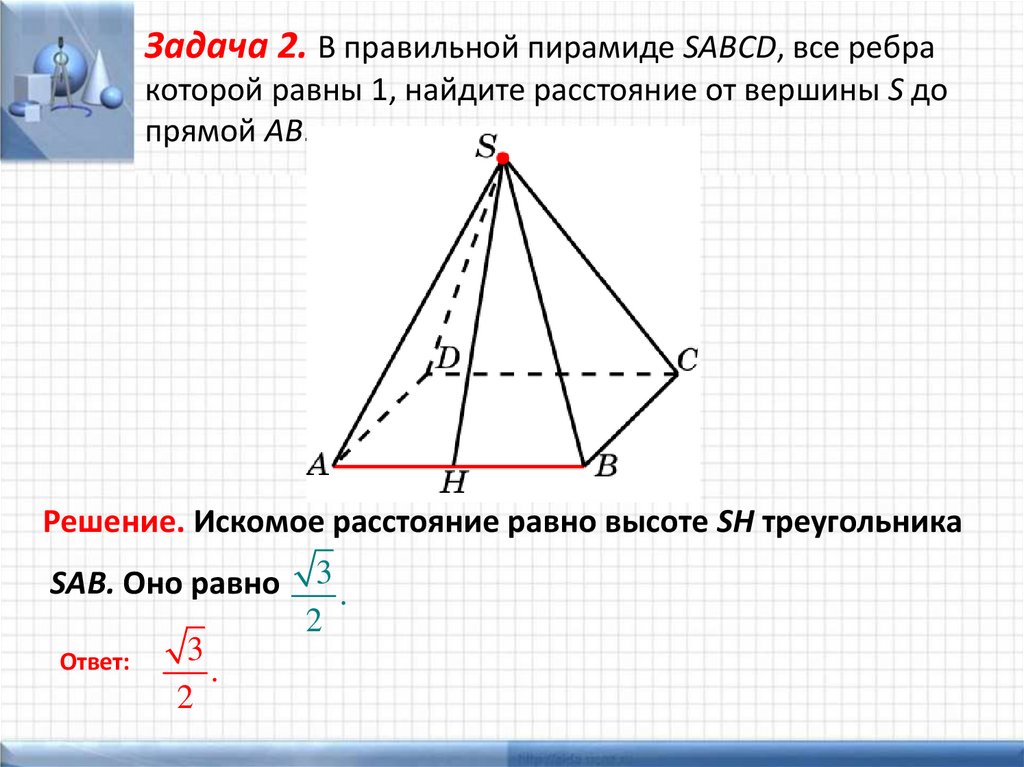
Задача 2. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите расстояние от вершины S до
прямой AB.
Решение. Искомое расстояние равно высоте SH треугольника
SAB. Оно равно 3 .
2
3
Ответ:
.
2

4.

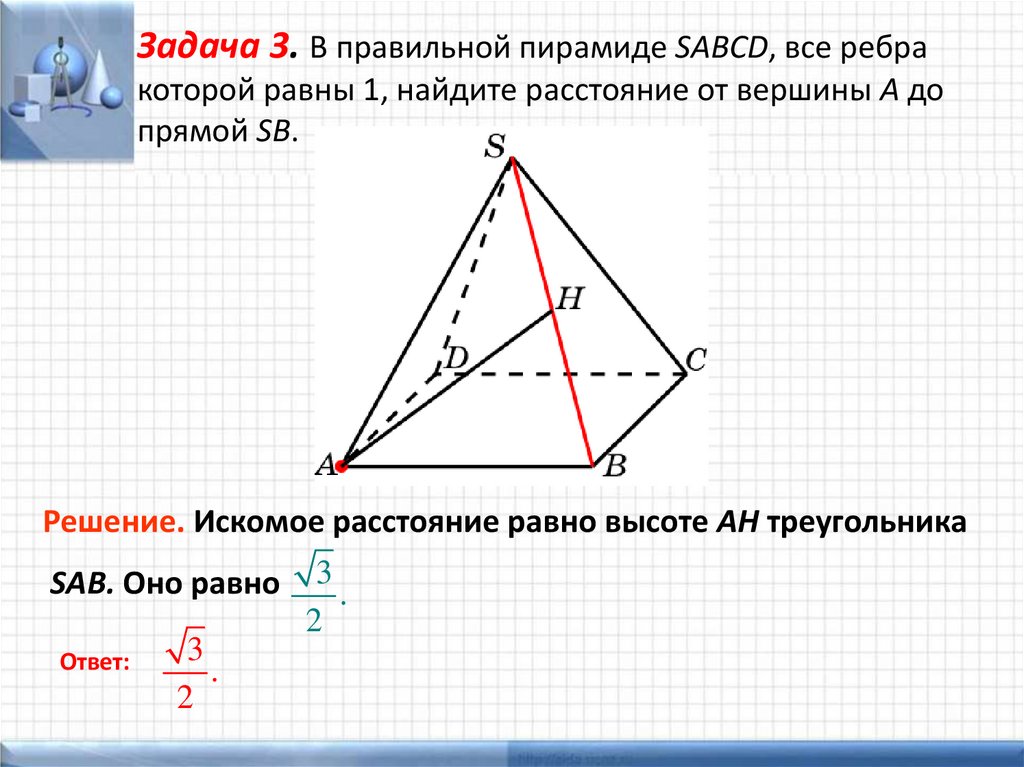
Задача 3. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите расстояние от вершины A до
прямой SB.
Решение. Искомое расстояние равно высоте AH треугольника
SAB. Оно равно 3 .
2
3
Ответ:
.
2

5.

Задача 4. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите расстояние от вершины A до
прямой SC.
Решение. Треугольник SAC прямоугольный. Искомое
расстояние равно катету SA и равно 1.
Ответ: 1.

6.

Задача 5. В правильной пирамиде SABCD, боковые ребра
которой равны 2, а ребра основания – 1, найдите
расстояние от вершины S до прямой AD.
Решение. Искомое расстояние равно высоте SH треугольника
SAD. Оно равно 3.
Ответ:
3.

7.

Задача 6. В правильной пирамиде SABCD, боковые ребра которой
равны 2, а ребра основания – 1, найдите расстояние от точки A до
прямой SB.
Решение. Искомое расстояние равно высоте AH треугольника
SAB. Оно равно 15 .
4
Ответ: 15 .
4

8.

Задача 7. В правильном тетраэдре ABCD найдите расстояние
от вершины D до плоскости ABC.
Решение. Обозначим E середину BC. Искомое расстояние
равно высоте DH треугольника ADE, для которого DE =
3
3
, HE =
. Следовательно, DH = 6 .
6
2
3
6
Ответ:
.
3

9.

Задача 8. Основанием треугольной пирамиде SABC
является прямоугольный треугольник с катетами,
равными 1. Боковые ребра пирамиды равны 1. Найдите
расстояние от вершины S до плоскости ABC.
2
Ответ:
.
2
Решение. Из равенства боковых ребер
следует, что основанием
перпендикуляра, опущенного из
вершины S на плоскость ABC, является
центр окружности, описанной около
треугольника ABC, т.е. середина D
стороны AC. Треугольник ACS –
прямоугольный и равнобедренный.
Следовательно, искомый
перпендикуляр SD равен 2 .
2

10.

Задача 9. В правильной пирамиде SABCD, все ребра которой равны 1,
найдите расстояние от вершины S до плоскости ABC.
Решение. Искомое расстояние равно высоте SO треугольника
SAC, в котором SA = SC = 1, AC = 2. Следовательно, SO = 2 .
2
2
Ответ:
.
2

11.

Задача 10. В правильной пирамиде SABCD, все ребра которой
равны 1, найдите расстояние от точки A до плоскости SBD.
Ответ:
2
.
2

12.

Задача 11. В правильной 6-ой пирамиде SABCDEF, боковые ребра
которой равны 2, а ребра основания – 1, найдите расстояние от
вершины S до плоскости ABC.
Решение. Искомое расстояние равно высоте SO
равностороннего треугольника SAD. Оно равно 3.
Ответ:
3.

13.

Задача 12. В правильной 6-ой пирамиде SABCDEF,
боковые ребра которой равны 2, а ребра основания – 1,
найдите расстояние от точки A до плоскости SBE.
Ответ:
3
.
2

14.

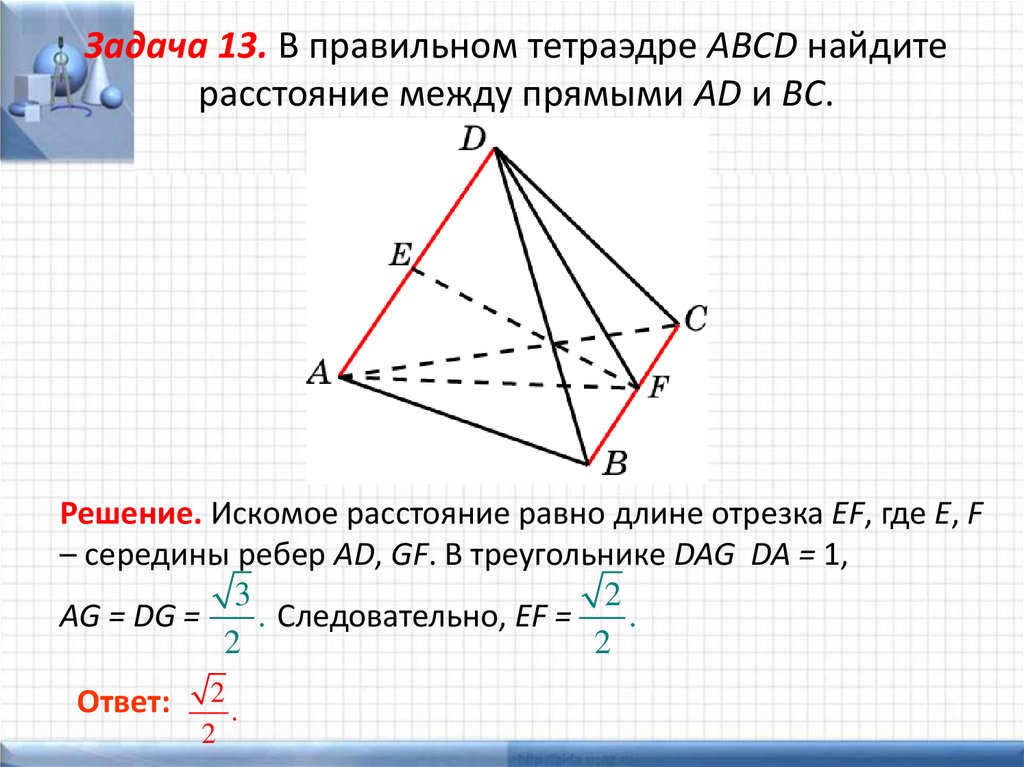
Задача 13. В правильном тетраэдре ABCD найдите
расстояние между прямыми AD и BC.
Решение. Искомое расстояние равно длине отрезка EF, где E, F
– середины ребер AD, GF. В треугольнике DAG DA = 1,
3
2
. Следовательно, EF =
AG = DG =
.
2
2
Ответ:
2
.
2

15.

Задача 14. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите расстояние между прямыми
SA и BD.
Ответ: 1.

16.

Задача 15. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите расстояние между прямыми SA и
BD.
Решение. Искомое расстояние равно высоте OH треугольника
SAO, где O – середина BD. В прямоугольном треугольнике SAO
2
1
. Следовательно, OH = .
имеем: SA = 1, AO = SO =
2
2
1
Ответ: .
2

17.

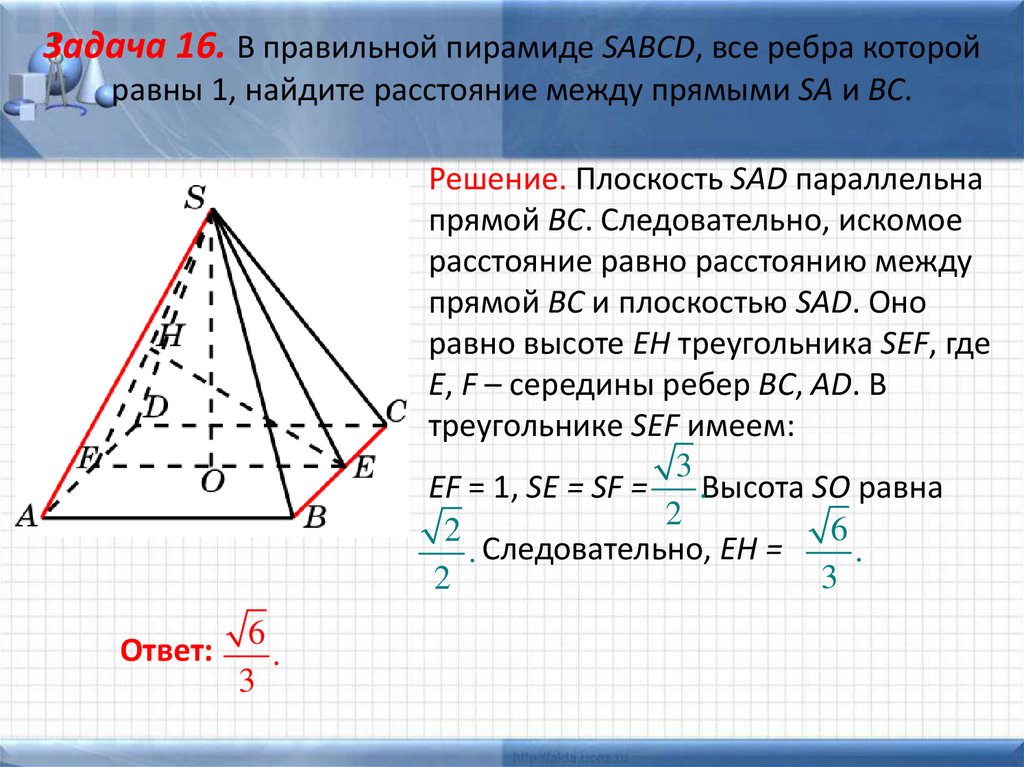
Задача 16. В правильной пирамиде SABCD, все ребра которой
равны 1, найдите расстояние между прямыми SA и BC.
Решение. Плоскость SAD параллельна
прямой BC. Следовательно, искомое
расстояние равно расстоянию между
прямой BC и плоскостью SAD. Оно
равно высоте EH треугольника SEF, где
E, F – середины ребер BC, AD. В
треугольнике SEF имеем:
3
EF = 1, SE = SF =
.Высота SO равна
2
6
2
.
. Следовательно, EH =
3
2
6
Ответ:
.
3

18.

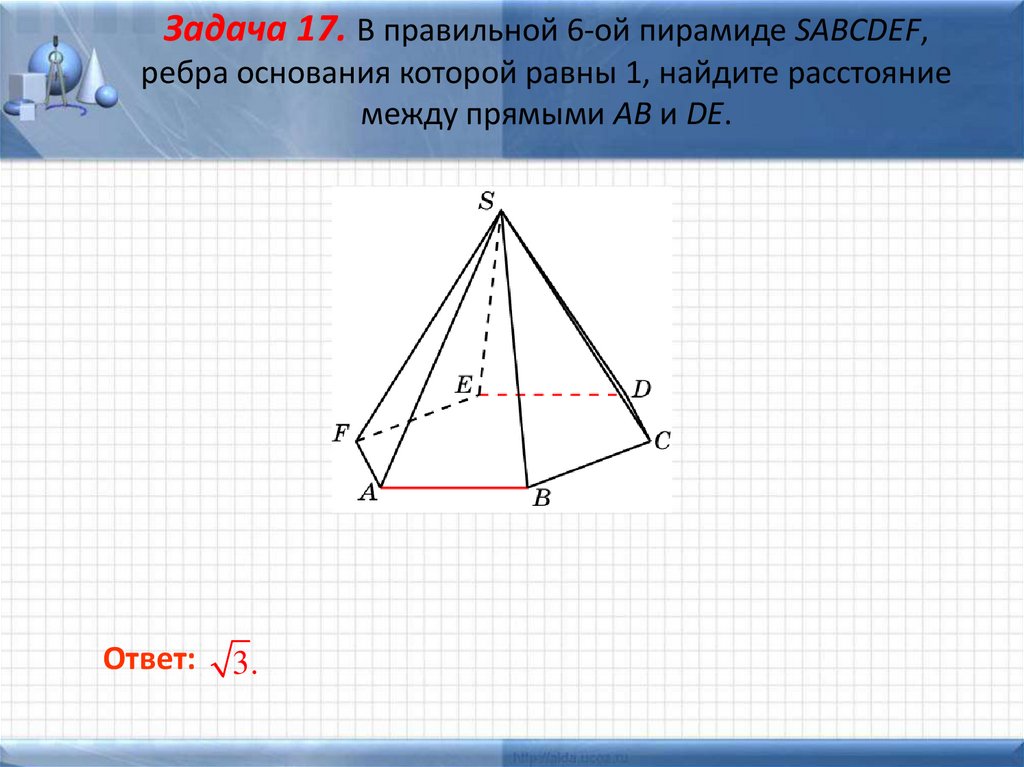
Задача 17. В правильной 6-ой пирамиде SABCDEF,
ребра основания которой равны 1, найдите расстояние
между прямыми AB и DE.
Ответ:
3.

19.

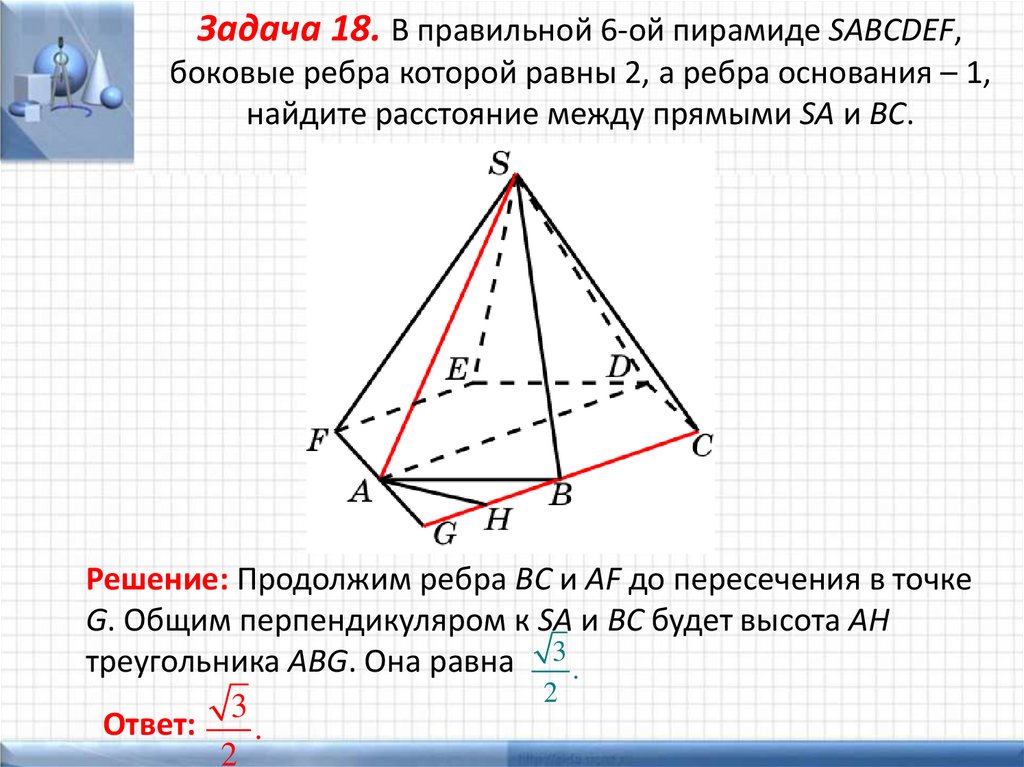
Задача 18. В правильной 6-ой пирамиде SABCDEF,
боковые ребра которой равны 2, а ребра основания – 1,
найдите расстояние между прямыми SA и BC.
Решение: Продолжим ребра BC и AF до пересечения в точке
G. Общим перпендикуляром к SA и BC будет высота AH
треугольника ABG. Она равна 3 .
2
3
Ответ:
.
2

20.

Задача 19. В правильной 6-ой пирамиде SABCDEF,
боковые ребра которой равны 2, а ребра основания – 1,
найдите расстояние между прямыми SA и BF.
Решение: Искомым расстоянием
является высота GH треугольника SAG,
где G – точка пересечения BF и AD. В
треугольнике SAG имеем:
3
SA = 1, AG =
, высота SO равна 3.
2
Отсюда находим GH =0,75.
Ответ: 0,75.

21.

Задача 20. В правильном тетраэдре ABCD найдите угол
между прямыми AD и BD.
Ответ: 60o.

22.

Задача 21. В правильном тетраэдре ABCD найдите угол
между прямыми AD и BC.
Решение. Через середину E ребра BC и прямую AD проведем
плоскость. Она будет перпендикулярна BC, т.к. AE и DE
перпендикулярны BC. Следовательно, AD перпендикулярна BC,
т.е. искомый угол равен 90о.
Ответ: 90о.

23.

Задача 22. В правильном тетраэдре ABCD точка E –
середина ребра AB. Найдите угол между прямыми AD и CE.
Решение. Через точку E проведем прямую EF, параллельную AD.
Искомым углом будет угол CEF. В треугольнике CEF имеем
1
3
3
.
cos
.
EF = , CE = CF =
Следовательно,
2
2
6
3
.
Ответ: cos
6

24.

Задача 23. В правильном тетраэдре ABCD
точки E, F, G – середины ребер AB, BD, CD.
Найдите угол EFG.
Решение. Прямые EF и FG параллельны прямым AD и BC.
Следовательно, угол между ними равен 90о.
Ответ: 90о.

25.

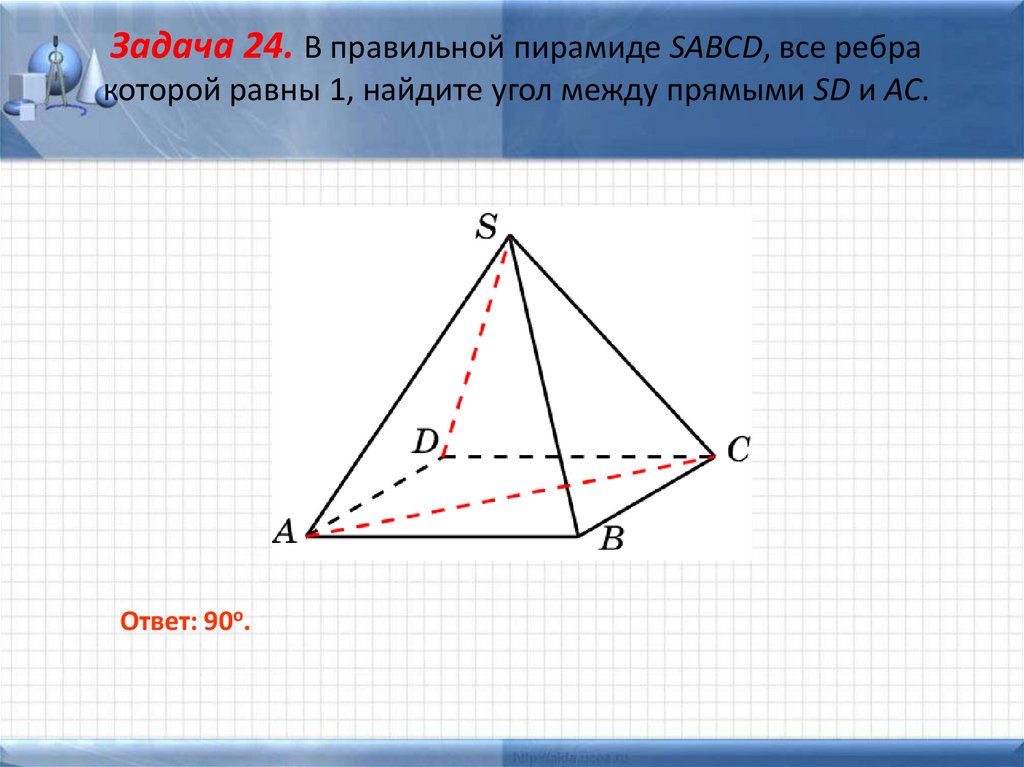
Задача 24. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите угол между прямыми SD и AC.
Ответ: 90о.

26.

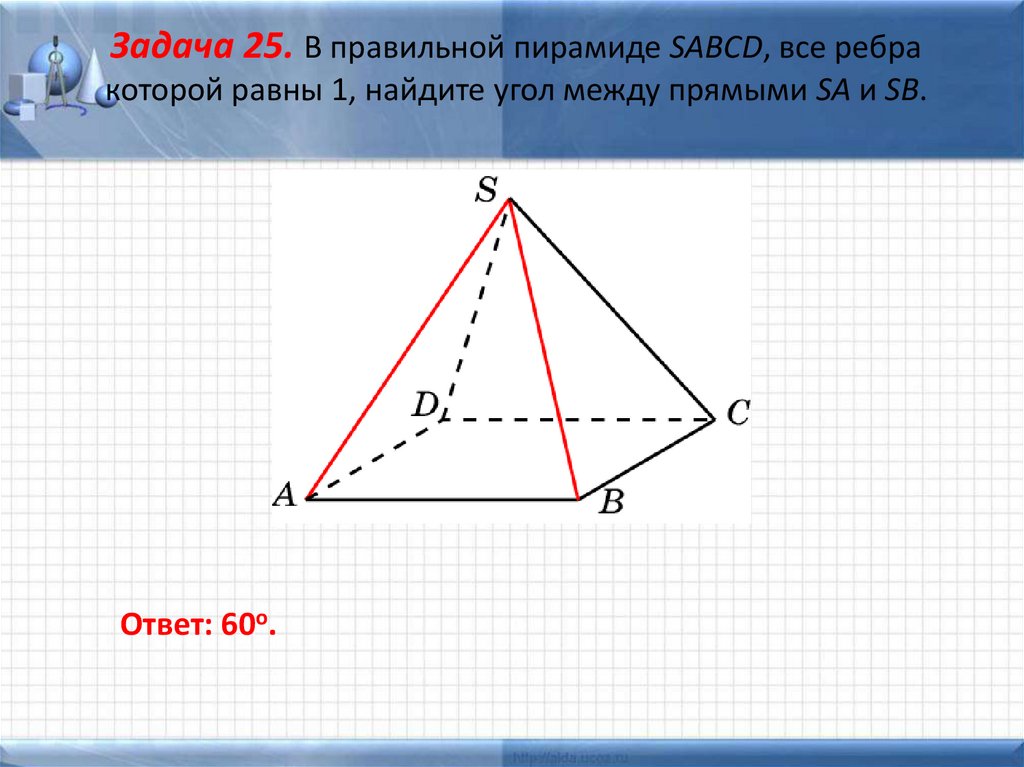
Задача 25. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите угол между прямыми SA и SB.
Ответ: 60о.

27.

Задача 26.
В правильной четырехугольной пирамиде SABCD, все
ребра которой равны 1, найдите угол между прямыми
AB и SC.
Ответ: 60o.

28.

Задача 27. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите угол между прямыми SA и SC.
Решение. В треугольнике SAC SA = SC = 1, AC =
Следовательно, искомый угол равен 90о.
Ответ: 90о.
2

29.

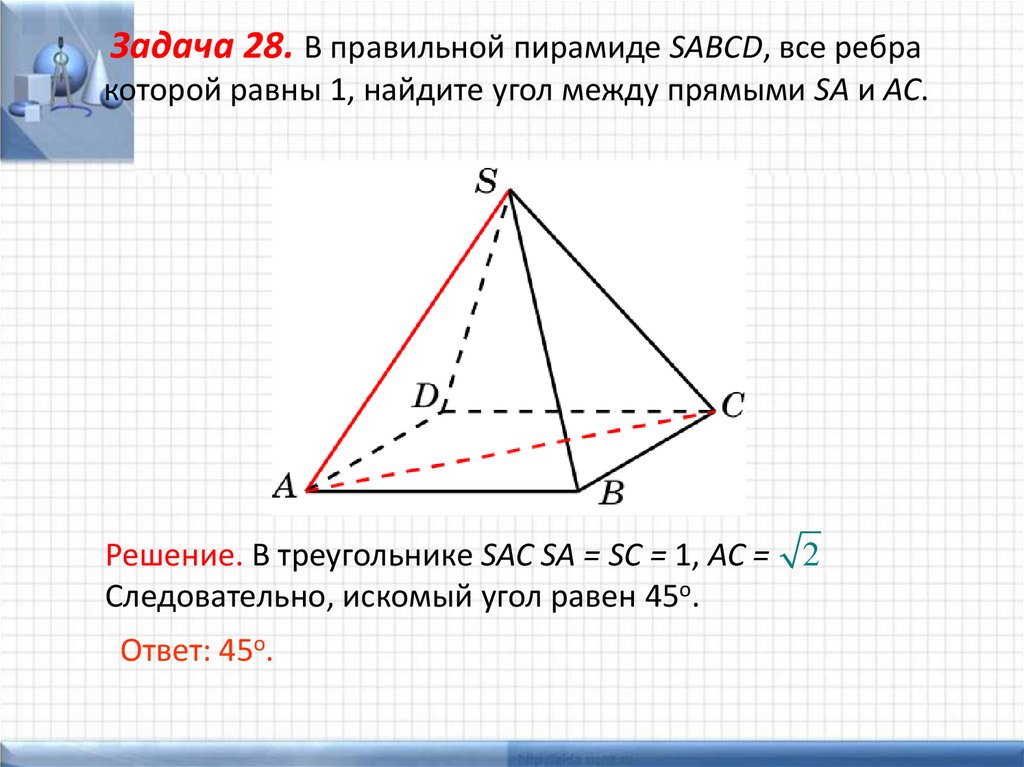
Задача 28. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите угол между прямыми SA и AC.
Решение. В треугольнике SAC SA = SC = 1, AC = 2
Следовательно, искомый угол равен 45о.
Ответ: 45о.

30.

Задача 29. В правильной пирамиде SABCD, все ребра
которой равны 1, найдите угол между прямыми SA и BD.
Решение. Прямая AC является ортогональной проекцией
прямой SA на плоскость ABC. Она перпендикулярна BD.
Следовательно, SA и BD также перпендикулярны.
Ответ: 90о.

31.

Задача 30. В правильной пирамиде SABCD, все ребра
которой равны 1, точка E – середина ребра SC. Найдите угол
между прямыми AD и BE.
Решение. Искомый угол равен углу CBE. Он равен 30о.
Ответ: 30о.

32.

Задача 31. В правильном тетраэдре ABCD найдите угол
между прямой AD и плоскостью ABC.
Решение. Пусть E – середина ребра BC. Искомый угол равен
углу DAE. В треугольнике DAE имеем: AD = 1, AE = DE = 3 .
3
Используя теорему косинусов, получим cos
.
3
3
Ответ: cos
3
.
2

33.

Задача 32. В правильной пирамиде SABCD, все ребра которой
равны 1, найдите угол между прямой SA и плоскостью ABC.
Решение: Искомый угол равен углу SAC. В треугольнике SAC
имеем: SA = SC = 1, AC = 2. Следовательно, искомый угол
равен 45о.
Ответ: 45о.

34.

Задача 33. В правильной пирамиде SABCD, все ребра которой
равны 1, найдите угол между прямой SA и плоскостью SBD.
Решение: Искомый угол равен углу SOA, где O – середина BD. В
2
прямоугольном треугольнике SOA имеем: SA = 1, AO =
.
2
Следовательно, искомый угол равен 45о.
Ответ: 45о.

35.

Задача 34. В правильной пирамиде SABCD, все ребра которой
равны 1, найдите угол между прямой AB и плоскостью SAD.
Решение. Пусть E, F – середины ребер AD и BC. Искомый угол
равен углу SEF. В треугольнике SEF имеем: EF = 1, SE = SF = 3 .
3
Используя теорему косинусов, получим cos
.
3
3
Ответ: cos
3
.
2

36.

Задача 35. В правильной 6-ой пирамиде SA…F, боковые
ребра которой равны 2, а ребра основания – 1, найдите угол
между прямой SA и плоскостью ABC.
Решение. Искомый угол равен углу SAD. Треугольник SAD
равносторонний. Следовательно, = 60о.
Ответ: 60о.

37.

Задача 36. В тетраэдре ABCD, ребра которого равны 1,
найдите угол между плоскостями ABC и BCD.
Решение: Пусть E – середина BC. Искомым линейным углом
является угол AED. В треугольнике AED имеем:
1
3
cos
.
AD = 1, AE = DE =
По. теореме косинусов находим
3
2
1
cos
.
Ответ:
3

38.

Задача 36. В правильной пирамиде SABCD, все ребра которой
равны 1, найдите угол между плоскостями SBC и ABC.
Решение: Пусть E, F – середины ребер BC и AD, O – центр
основания. Искомым линейным углом является угол SEF.
3
1
.
В прямоугольном треугольнике SEO имеем EO = , SE =
2
2
3
.
Следовательно, cos
3
3
cos
.
Ответ:
3

39.

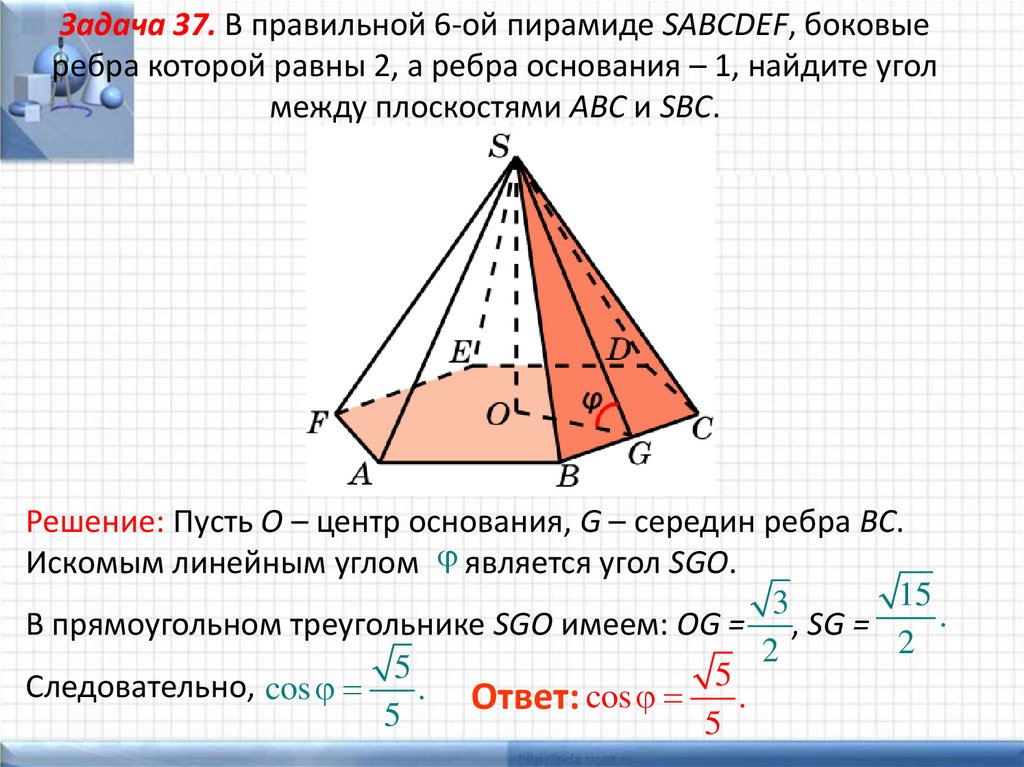
Задача 37. В правильной 6-ой пирамиде SABCDEF, боковые
ребра которой равны 2, а ребра основания – 1, найдите угол
между плоскостями ABC и SBC.
Решение: Пусть O – центр основания, G – середин ребра BC.
Искомым линейным углом является угол SGO.
15
3
.
В прямоугольном треугольнике SGO имеем: OG = , SG =
2
2
5
Следовательно, cos
. Ответ: cos 5 .
5
5

40.

Задача 38. В правильной 6-ой пирамиде SABCDEF, боковые ребра
которой равны 2, а ребра основания – 1, найдите косинус
двугранного угла, образованного гранями SAB и SBC.
Решение: В треугольниках SAB и SBC опустим высоты AH и CH на
сторону SB. Искомым линейным углом является угол AHC. В
прямоугольном треугольнике AHC имеем: AC = 3 , AH = CH =
15 По теореме косинусов находим
3
.
cos .
4
5
Ответ: -0,6

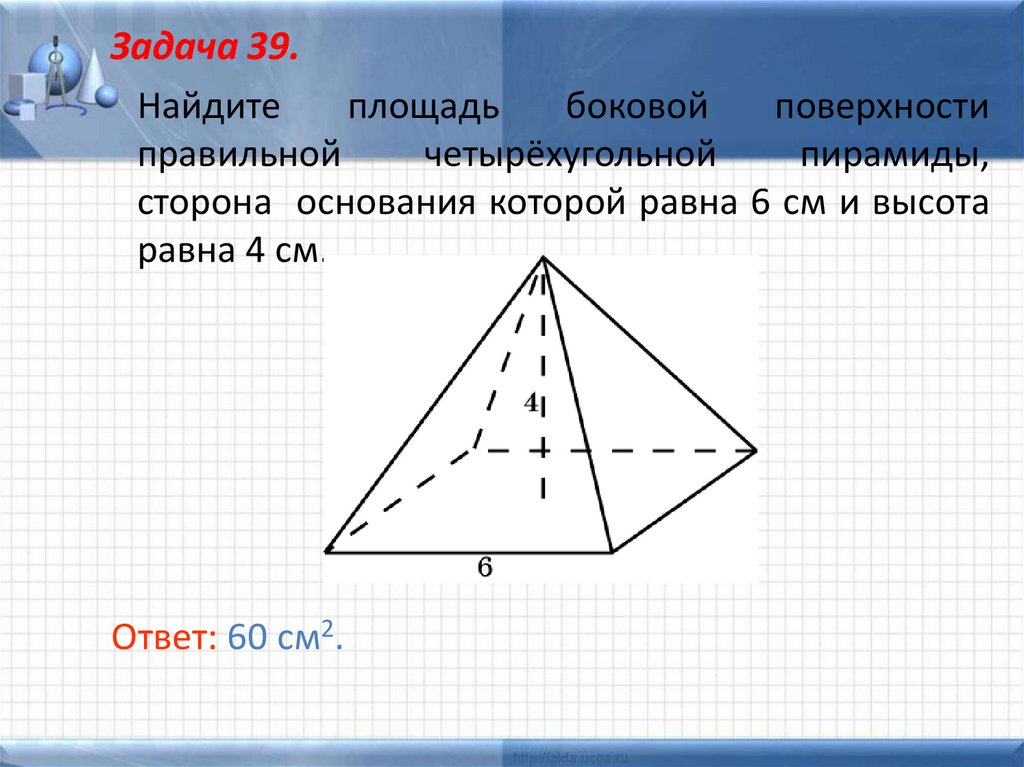
41. Задача 39.

Найдите
площадь
боковой
поверхности
правильной
четырёхугольной
пирамиды,
сторона основания которой равна 6 см и высота
равна 4 см.
Ответ: 60 см2.

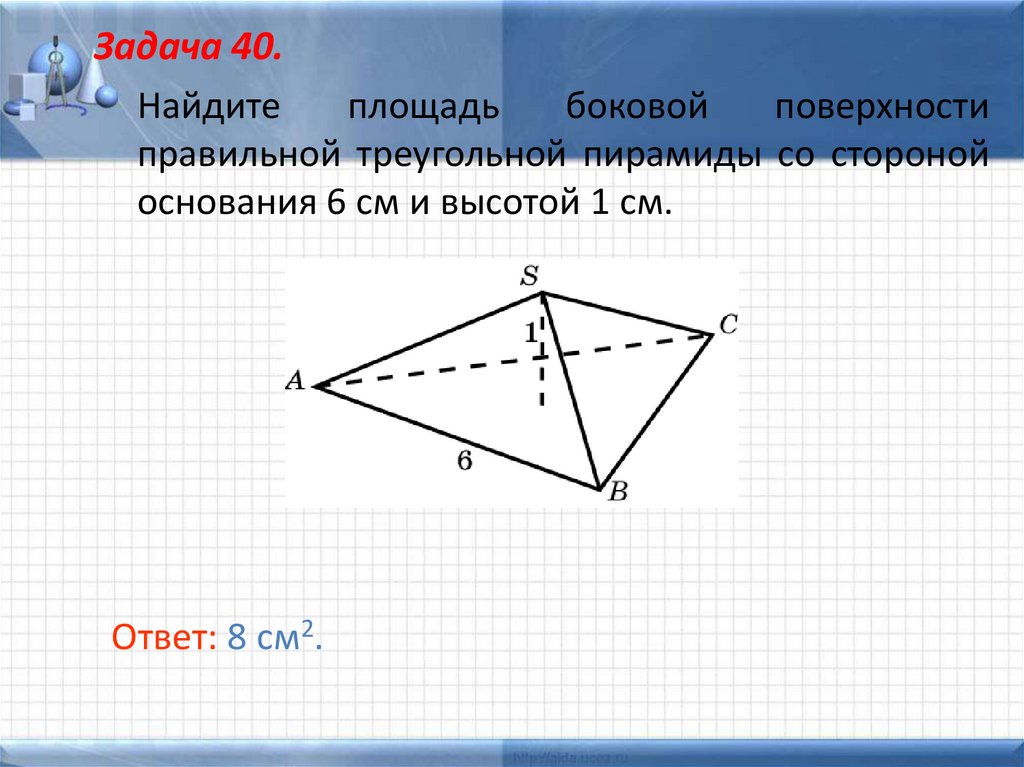
42. Задача 40.

Найдите
площадь
боковой
поверхности
правильной треугольной пирамиды со стороной
основания 6 см и высотой 1 см.
Ответ: 8 см2.

43. Задача 41.

Найдите
площадь
боковой
поверхности
правильной шестиугольной пирамиды со
стороной основания 4 см и высотой 2 см.
Ответ: 48 см2.

44. Задача 42.

Как изменятся площади боковой и полной поверхностей
пирамиды, если все её рёбра:
а) увеличить в 2 раза; б) уменьшить в 5 раз?
Ответ: а) Увеличатся в 4 раза; б) уменьшатся в 25 раз.

45. Задача 43.

Развёртка поверхности правильной треугольной
пирамиды представляет собой равносторонний
треугольник, площадь которого равна 80 см2. Найдите
площадь грани пирамиды.
Ответ: 20 см2.

46. Задача 44.

Чему равна площадь поверхности правильного
тетраэдра с ребром 1?
Ответ: 3.