Похожие презентации:
Геометрия в Заданиях ЕГЭ
1. Геометрия в Заданиях ЕГЭ
2. Результаты ЕГЭ по математике 2013
В этом году экзамен сдавали 860 840человек. 754 776 из них – выпускники
текущего года. То есть, 106 064 человека
сдавали ЕГЭ повторно, либо впервые – для
поступления в вуз.
Всего было проведено 2 888 104 «человекэкзаменов» (если расценивать присутствие
одного человека на экзамене как
отдельный экзамен).
Таким образом, было сдано 1 166 424
человек-экзамена по выбору.
3.
Результаты ЕГЭ по математике 2013Средний тестовый балл по
математике в России 48,7.
538 выпускников сдали ЕГЭ по
математике на 100 баллов.
7 человек из Саратовской области
получили 100 баллов.
43% выпускников не приступили к
части С с развернутым решением.
4.
Результаты ЕГЭ по математике 2013Согласно результатам пересдач и
апелляций, 2,24 % учеников (16 635
человек) не получили аттестат о среднем
(полном) общем образовании.
В том числе, около 500 человек были
лишены права пересдать ЕГЭ в текущем
году за нарушение правил сдачи ЕГЭ.
Более того, в Якутии возбуждено 5 дел об
административном правонарушении.
5.
Результаты ЕГЭ по математике 2013Если говорить об образовательных тенденциях, то,
как отмечают организаторы ЕГЭ, они не самые
радужные. К сожалению, говорить о росте
образованности пока не приходится, особенно в
точных науках. К примеру, задание B1 – про
таблетки – не выполнили 150 000 учащихся (около
17 %). Один из учащихся даже предложил в ответе
дать ребёнку 31 500 таблеток.
В целом экзамен по математике показал
незначительный – на 4 тестовых балла – рост
общероссийского среднего балла ЕГЭ.
6. Результаты ЕГЭ по математике 2013
Всего в Саратове над тестами и задачкамиразмышляли более четырех тысяч
выпускников. Из них почти две сотни, 197
человек, провалили этот экзамен школьники набрали меньше 24 баллов (тот
минимальный порог, который нужно
преодолеть ). А вот отличниками стали
всего четверо саратовских
одиннадцатиклассников - точная наука явно
далась школьникам сложнее, чем родной
язык. На ЕГЭ по русскому, напомним,
максимальный балл набрали 24 ученика.
7. Результаты ЕГЭ по математике 2013
Тем не менее этот результат всеравно лучше прошлогодних: для
сравнения, в 2011 году ЕГЭ по
математике в Саратове на сто баллов
написал лишь один ученик, а в 2012
году и вовсе никому не удалось не
сделать ни одной ошибки. Средний
балл по городу также увеличился и
составил 54,3, тогда как в 2012 году
школьники набирали 42,6.
8. Расстояние от точки до плоскости
9. C 2. Радиус основания конуса равен 5, а его высота равна 12. Плоскость сечения содержит вершину конуса и хорду основания, длина
C 2. Радиус основания конуса равен 5, а его высота равна 12.Плоскость сечения содержит вершину конуса и хорду основания,
длина которой равна 6. Найдите расстояние от центра основания
конуса до плоскости сечения.
Сечение конуса плоскостью, содержащей его
вершину S и хорду АВ 6 - треугольник ASB. В
равных прямоугольных треугольниках SOA
и SOB, где О — центр основания конуса,
откуда ОА ОВ 5, SO 12,
SA SB OB 2 SO2 13.
Пусть SH — высота и медиана равнобедренного
треугольника ASB,
SH SB 2 HB 2 , SH 169 9 4 10.
Тогда отрезок ОН — высота и медиана равнобедренного треугольника AOB,
OH 4.
Плоскость SOH перпендикулярна плоскости ASB, так как прямые SH и
OH перпендикулярны прямой АВ. Поэтому расстояние от точки О до
плоскости ASB равно высоте ОМ прямоугольного
OH SO 6 10
треугольника SOH, проведенной к гипотенузе
OM
6 10
Ответ :
.
5
SH
5
.
10. Расстояние от точки до прямой
11. C 2. Длины ребер AB, AA1 и AD прямоугольного параллелепипеда ABCDA1B1C1D1 равны соответственно 12, 16 и 15. Найдите расстояние
C 2. Длины ребер AB, AA1 и AD прямоугольногопараллелепипеда ABCDA1B1C1D1 равны соответственно 12,
16 и 15. Найдите расстояние от вершины A1 до прямой BD1.
Из вершины А1 опускаем
перпендикуляр на ВD1.
Так как А1D1 перпендикулярна
плоскости АА1В, то
А1D1 перпендикулярен А1В.
Следовательно А1Евысота прямоугольного
треугольника А1BD1.
A1D1 A1B
A1E
, A1B A1 A2 AB 2 20,
D1B
20 15
BD1 A1 A AB A1 D1 25, A1E
12
25
2
2
2
Ответ:12.
12. Задачи на сечение
13. C 2. Точка Е — середина ребра ВВ1 куба ABCDA1B1C1D1 . Найдите площадь сечения куба плоскостью D1AE , если ребра куба
C 2. Точка Е — середина ребра ВВ1 куба ABCDA1B1C1D1 .Найдите площадь сечения куба плоскостью D1AE , если ребра
куба равны 4.
Прямая АЕ пересекает прямую А1В1 в
точке К, а прямая D1K пересекает
С1В1 в его середине , точке
F. Искомое сечение – плоскость D1FEA.
Из подобия треугольников AD1K и
EFK следует, что
М
S AD1FE
3
3 1
S AD1K AD1 h
4
4 2
Высота КМ=h , ее длину находим из треугольника АМК
h MK AK AM , h (4 5 ) (2 2 ) 6 2.
3 1
S AD1FE 4 2 6 2 18.
4 2
Ответ:18.
2
2
2
2
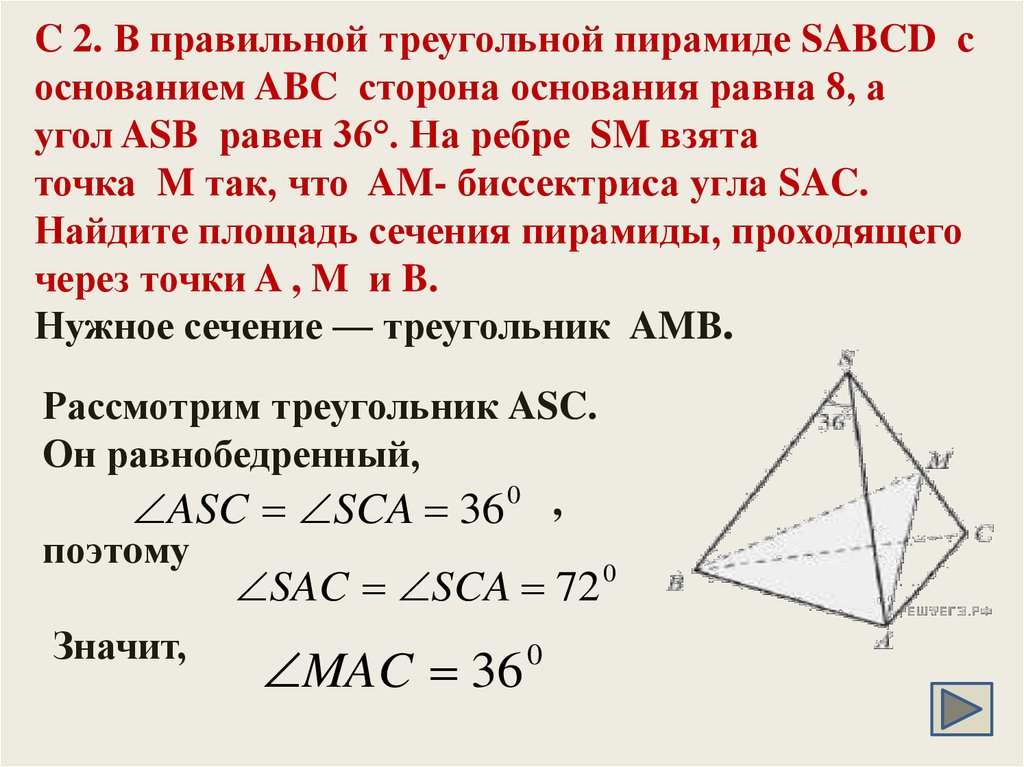
14. C 2. В правильной треугольной пирамиде SABCD с основанием ABC сторона основания равна 8, а угол ASB равен 36°. На ребре
C 2. В правильной треугольной пирамиде SABCD соснованием ABC сторона основания равна 8, а
угол ASB равен 36°. На ребре SM взята
точка M так, что AM- биссектриса угла SAC.
Найдите площадь сечения пирамиды, проходящего
через точки A , M и B.
Нужное сечение — треугольник AMB.
Рассмотрим треугольник ASC.
Он равнобедренный,
ASC SCA 36 0 ,
поэтoму
0
SAC SCA 72
Значит,
MAC 36
0
15.
Ответ : 16 3.Рассмотрим теперь треугольник CAM . Сумма его
углов 1800 , значит, угол АМС равен 720 .
Следовательно, треугольник САМ равнобедренный, и
поэтому АМ=АС=8. Аналогично находим, что ВМ=8.
Таким образом, треугольник АМВ равносторонний
со стороной 8. Его площадь равна
82 3
16 3.
4
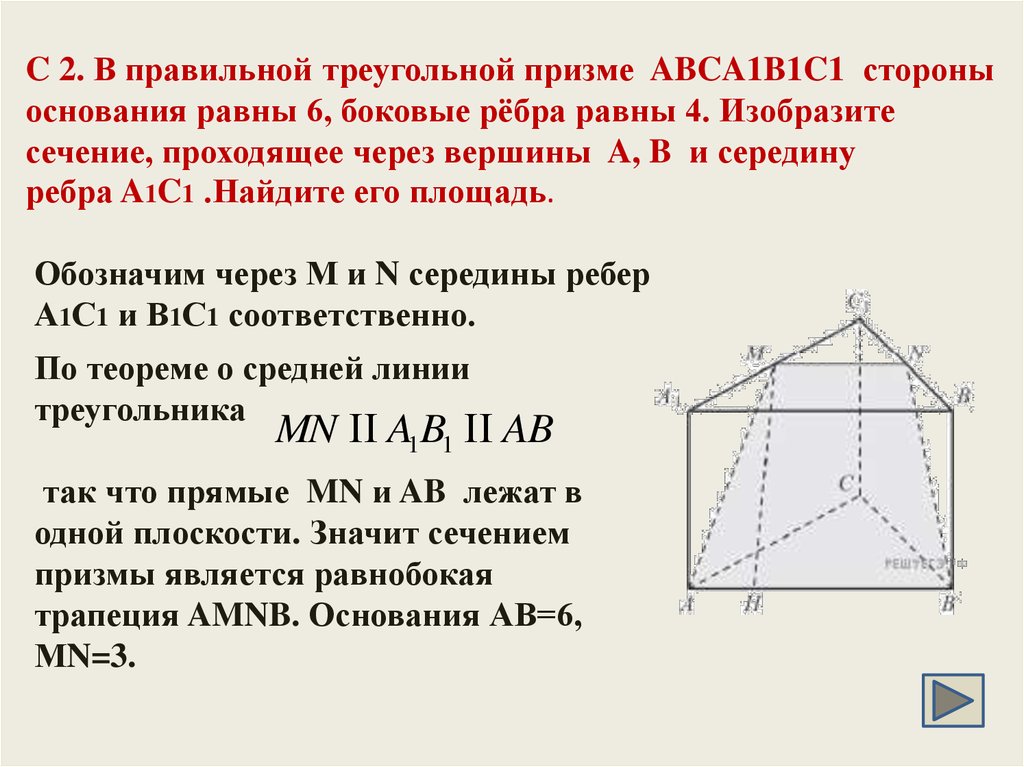
16. C 2. В правильной треугольной призме ABCA1B1C1 стороны основания равны 6, боковые рёбра равны 4. Изобразите сечение,
C 2. В правильной треугольной призме ABCA1B1C1 стороныоснования равны 6, боковые рёбра равны 4. Изобразите
сечение, проходящее через вершины A, B и середину
ребра A1C1 .Найдите его площадь.
Обозначим через М и N середины ребер
А1С1 и В1С1 соответственно.
По теореме о средней линии
треугольника
MN A1B1 AB
так что прямые MN и AB лежат в
одной плоскости. Значит сечением
призмы является равнобокая
трапеция AMNB. Основания АВ=6,
МN=3.
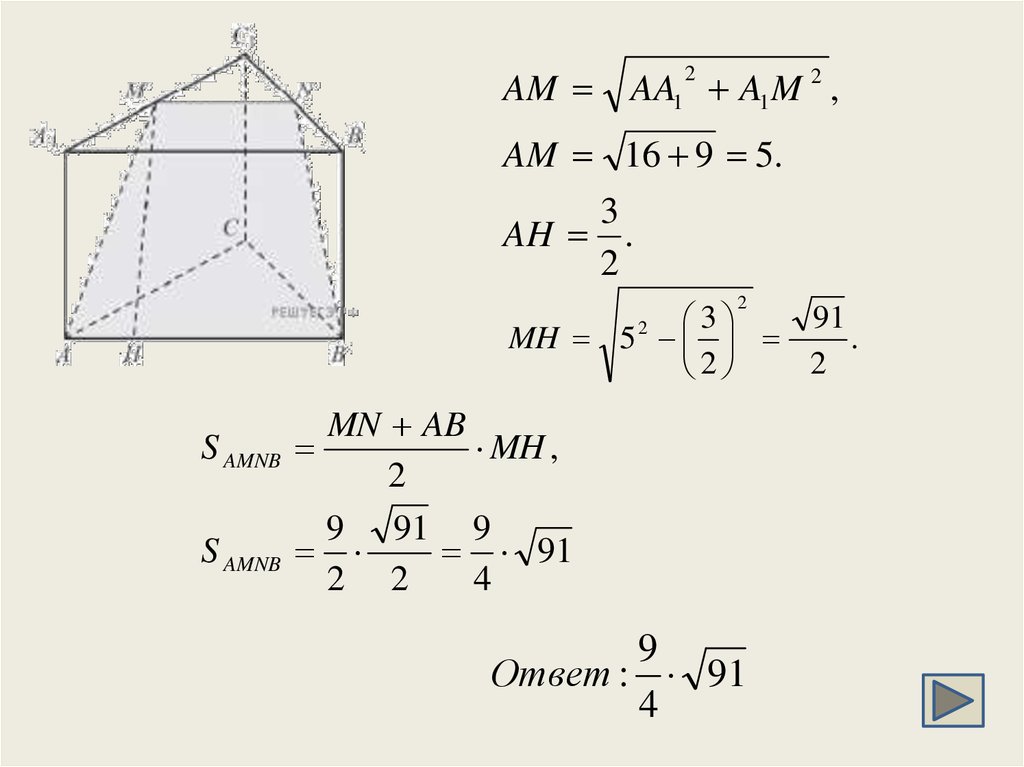
17.
AMAA1 A1 M 2 ,
2
AM 16 9 5.
3
AH .
2
2
91
3
2
MH 5
.
2
2
S AMNB
S AMNB
MN AB
MH ,
2
9 91 9
91
2 2
4
9
Ответ : 91
4
18. Угол между прямыми
19. C 2 . Точка E - середина ребра куба ABCDA1B1C1D1 . Найдите угол между прямыми AE и CA1 .
C2.Точка E - середина ребра куба ABCDA1B1C1D1 .
Найдите угол между прямыми AE и CA1 .
Примем ребро куба за единицу. Тогда
CA1 3
Проведём через точку A1 прямую,
параллельную AE . Она пересекает
продолжение ребра BB1 в точке F ,
1
причём
B1 F .
2
Искомый угол равен углу CA1F (или
смежному с ним). В прямоугольном
треугольнике A1B1F с прямым
углом B1
5
2
A1 F A1 B1 B1 F 2
.
2
20. В прямоугольном треугольнике CBF с прямым углом B
В прямоугольном треугольнике CBF с прямымуглом B
CF CB BF
2
2
13
.
2
В треугольнике CA1F
CF CA1 A1 F 2 2 cos CA1 F CA1 A1 F
2
2
CA1 A1 F 2 CF 2
15
cos CA1 F
,
2 CA1 A1 F
15
2
15
CA1 F arccos
.
15
15
Ответ: arccos
.
15
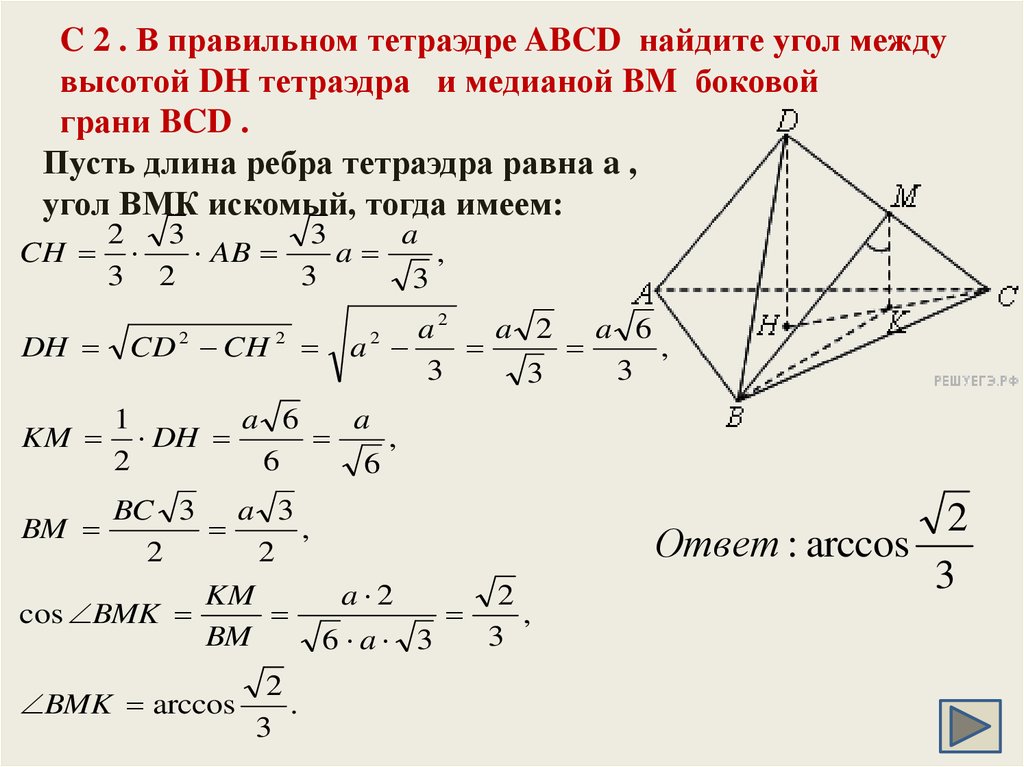
21. C 2 . В правильном тетраэдре ABCD найдите угол между высотой DH тетраэдра и медианой BM боковой грани BCD .
C 2 . В правильном тетраэдре ABCD найдите угол междувысотой DH тетраэдра и медианой BM боковой
грани BCD .
Пусть длина ребра тетраэдра равна a ,
угол ВМК искомый, тогда имеем:
2
3
3
a
CH
AB
a
,
3 2
3
3
DH
KM
CD CH
2
2
a2
a 2 a 6
a
,
3
3
3
2
1
a 6
a
DH
,
2
6
6
BC 3 a 3
,
2
2
KM
a 2
2
cos BMK
,
BM
3
6 a 3
BM
BMK arccos
2
.
3
2
Ответ : arccos
3
22. C 2. В правильной шестиугольной пирамиде SABCDEF стороны основания которой равны 1, а боковые ребра равны 2, найдите угол между
C 2. В правильной шестиугольнойпирамиде SABCDEF стороны основания которой
равны 1, а боковые ребра равны 2, найдите угол
между прямыми SB и CD.
Вместо прямой CD рассмотрим
параллельную ей прямую BE.
Искомый угол равен углу SBE.
Треугольник SBE равносторонний,
поскольку большая диагональ
правильного шестиугольника вдвое
больше его стороны: ВЕ=2СD
Следовательно, угол CBE=600 .
Ответ: 600
23. Угол между плоскостями
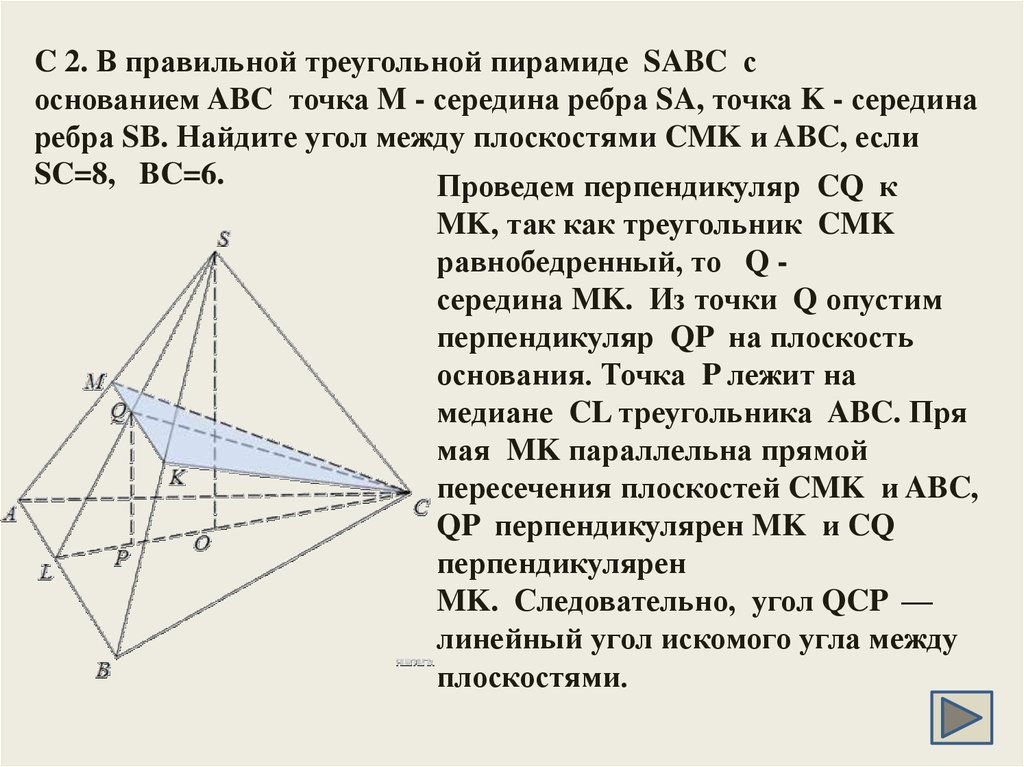
24. C 2. В правильной треугольной пирамиде SABC с основанием ABC точка M - середина ребра SA, точка K - середина ребра SB.
C 2. В правильной треугольной пирамиде SABC соснованием ABC точка M - середина ребра SA, точка K - середина
ребра SB. Найдите угол между плоскостями CMK и ABC, если
SC=8, BC=6.
Проведем перпендикуляр CQ к
MK, так как треугольник CMK
равнобедренный, то Q середина MK. Из точки Q опустим
перпендикуляр QP на плоскость
основания. Точка P лежит на
медиане CL треугольника ABC. Пря
мая MK параллельна прямой
пересечения плоскостей CMK и ABC,
QP перпендикулярен MK и CQ
перпендикулярен
MK. Следовательно, угол QCP —
линейный угол искомого угла между
плоскостями.
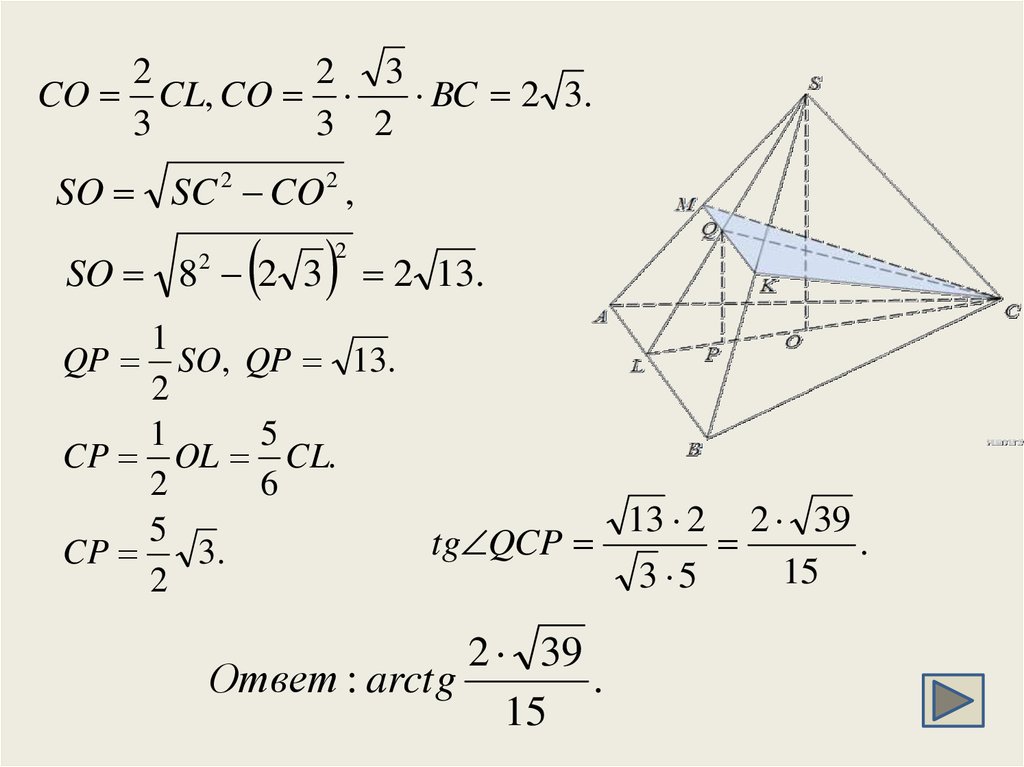
25.
22 3
CO CL, CO
BC 2 3.
3
3 2
SO SC 2 CO 2 ,
SO 8 2 3
2
2
2 13.
1
QP SO, QP 13.
2
1
5
CP OL CL.
2
6
13 2 2 39
5
tg QCP
.
CP
3.
15
3 5
2
2 39
Ответ : arctg
.
15
26. C 2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра: AB=6, AD=8, CC1=16. Найдите угол между плоскостями ABC
C 2. В прямоугольном параллелепипедеABCDA1B1C1D1 известны ребра: AB=6, AD=8, CC1=16.
Найдите угол между плоскостями ABC и A1DB.
Плоскости ABC и A1DB имеют
общую прямую BD. Проведем AH
перпендикуляр к BD. По теореме
о трех перпендикулярах A1H
перпендикулярен BD. Значит,
линейный угол двугранного угла,
образованного плоскостями
ABC и A1DB — это угол
A1HA. Из прямоугольного
треугольника BAD находим:
AB AD
AH
,
BD
48 24
AH
.
10
5
27.
Из прямоугольноготреугольника A1AH
находим:
AA1
tg A1 HA
,
AH
16 5 10
tg A1 HA
.
24
3
Значит, искомый угол равен
10
Ответ : arctg .
3
10
arctg .
3
28. Угол между прямой и плоскостью
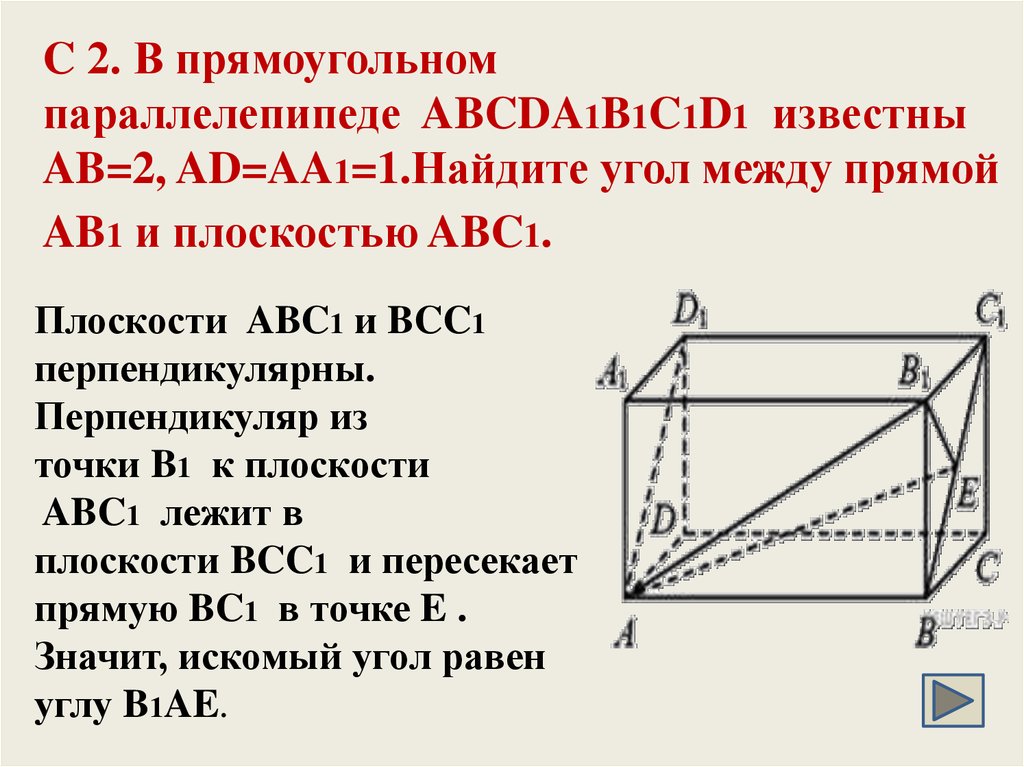
29. C 2. В прямоугольном параллелепипеде ABCDA1B1C1D1 известны AB=2, AD=AA1=1.Найдите угол между прямой AB1 и плоскостью ABC1.
C 2. В прямоугольномпараллелепипеде ABCDA1B1C1D1 известны
AB=2, AD=AA1=1.Найдите угол между прямой
AB1 и плоскостью ABC1.
Плоскости ABC1 и BCC1
перпендикулярны.
Перпендикуляр из
точки B1 к плоскости
ABC1 лежит в
плоскости BCC1 и пересекает
прямую BC1 в точке E .
Значит, искомый угол равен
углу B1AE.
30.
В прямоугольномтреугольнике B1AE
2
,
катет B1 E
2
гипотенуза AB1 5.
Поэтому
B1 E
sin B1 AE
.
AB1
1
Ответ : arcsin
.
10
1
3
1
sin B1 AE
,
B1 AE arccos
arctg arcctg 3.
10
3
10
1
B1 AE arcsin
.
10
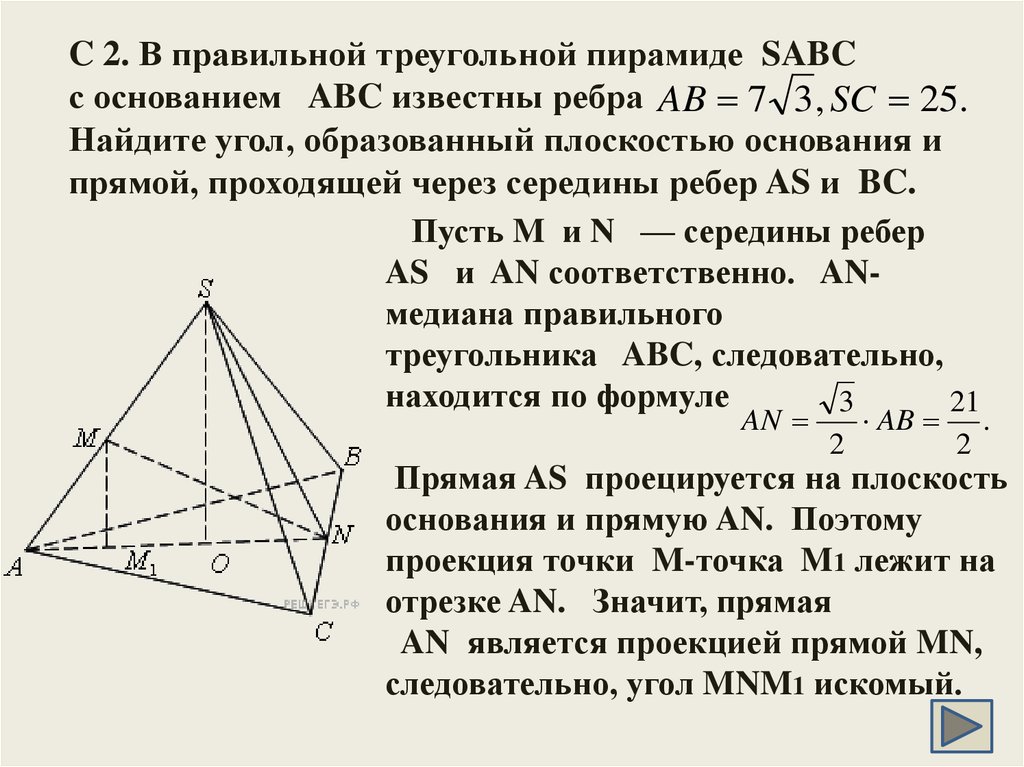
31. C 2. В правильной треугольной пирамиде SABC с основанием ABC известны ребра Найдите угол, образованный плоскостью
C 2. В правильной треугольной пирамиде SABCс основанием ABC известны ребра AB 7 3 , SC 25.
Найдите угол, образованный плоскостью основания и
прямой, проходящей через середины ребер AS и BC.
Пусть M и N — середины ребер
AS и AN соответственно. ANмедиана правильного
треугольника ABC, следовательно,
находится по формуле
3
21
AN
2
AB
2
.
Прямая AS проецируется на плоскость
основания и прямую AN. Поэтому
проекция точки M-точка M1 лежит на
отрезке AN. Значит, прямая
AN является проекцией прямой MN,
следовательно, угол MNM1 искомый.
32.
Поскольку MM1 параллелен SO, где О- центроснования, MM1 средняя линия треугольника SAO
2
2 3
3
AO CO AN AB
24 3 24.
3
3 2
3
2
AN 24
3
1
1
7
MM 1 SO
SC 2 CO 2 .
2
2
2
NM 1
Из прямоугольного треугольника
MM1N находим
MM 1
7
tg M 1 NM
.
NM 1 48
7
Ответ : arctg .
48

























 Математика
Математика








