Похожие презентации:
Многогранники. Понятие о правильных многогранниках. Призма, параллелепипед и его свойства
1. Тема 9.2 Многогранники. Понятие о правильных многогранниках. Призма, параллелепипед и его свойства.
2. Цель:
• ввести понятие правильного многогранника, выяснить, какимисвойствами обладают правильные многогранники; используя
свойства правильных многогранников, решать практические
задачи
План:
Понятие многогранника
Призма
Параллелепипед
Куб
3. Многогранники
Понятиемногогранника.
Призма.
4.
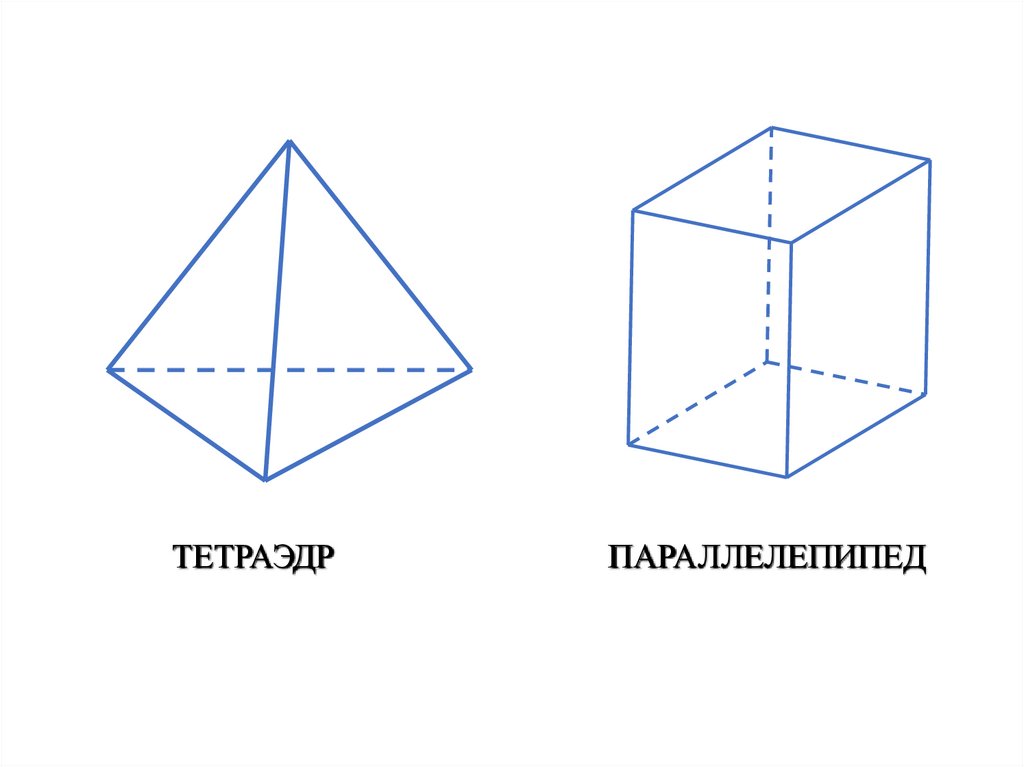
ТЕТРАЭДРПАРАЛЛЕЛЕПИПЕД
5.
Поверхность, составленную измногоугольников и
ограничивающую некоторое
геометрическое тело, будем
называть многогранной
поверхностью или
многогранником
6.
Примеры многогранниковТЕТРАЭДР
РОМБОУСЕЧЁННЫЙ
ИКОСОДОДЕКАЭДР
ПАРАЛЛЕЛЕПИПЕД
КУРНОСЫЙ КУБ
ОКТАЭДР
ЗВЁЗДЧАТЫЙ
ОКТАЭДР
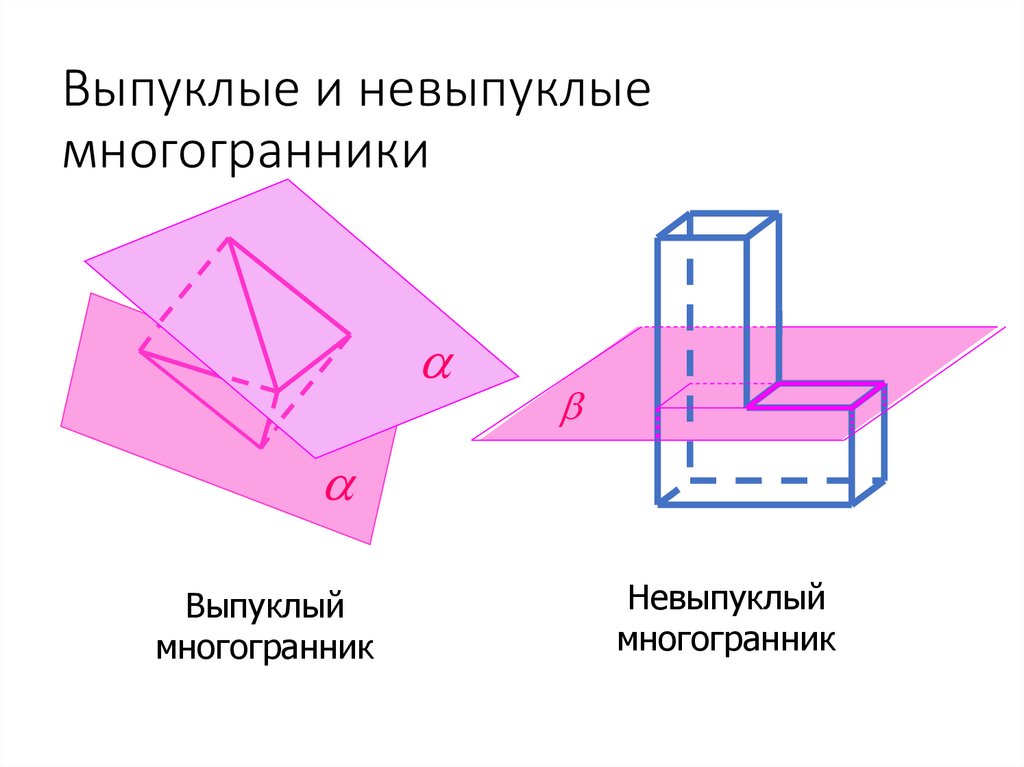
7. Выпуклые и невыпуклые многогранники
Выпуклыймногогранник
Невыпуклый
многогранник
8.
АBnn
BА11
А2
B
9.
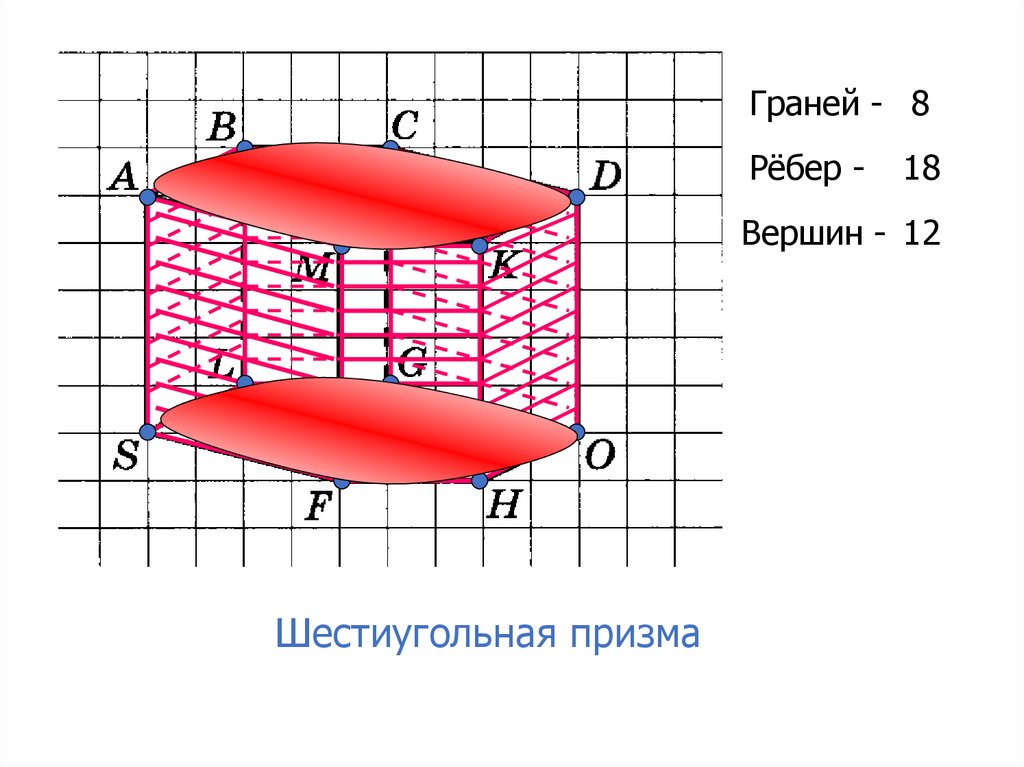
Граней - 8Рёбер -
18
Вершин - 12
Шестиугольная призма
10.
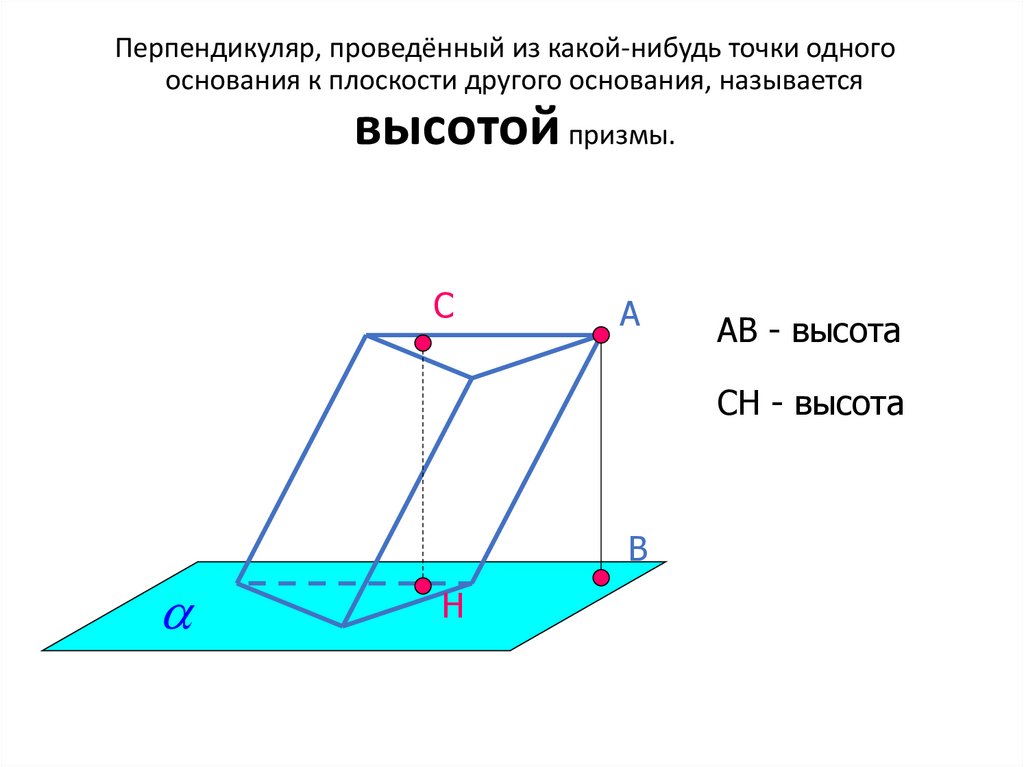
Перпендикуляр, проведённый из какой-нибудь точки одногооснования к плоскости другого основания, называется
высотой призмы.
С
А
АВ - высота
СН - высота
В
Н
11.
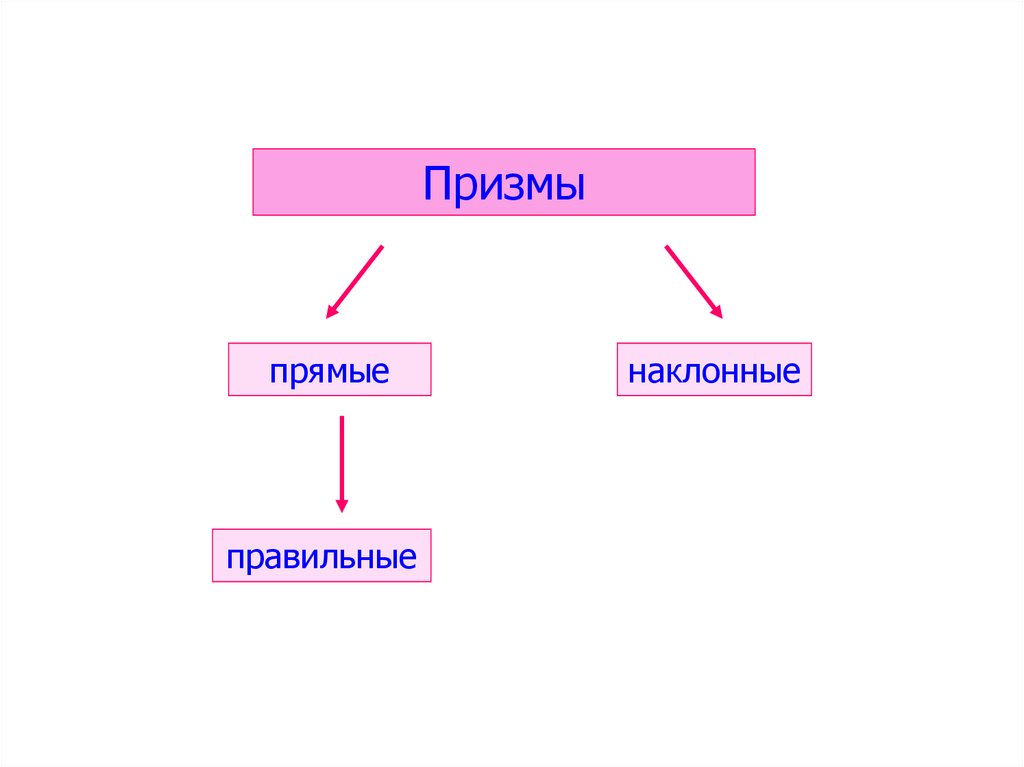
Призмыпрямые
правильные
наклонные
12. Прямые призмы
четырехугольнаяпризма, основаниями
которой являются
параллелограммы.
Все шесть граней
параллелепипедапараллелограммы.
13. Наклонные призмы
Основания (2)Ребра (12)
Вершины (8)
Боковые грани (4)
14.
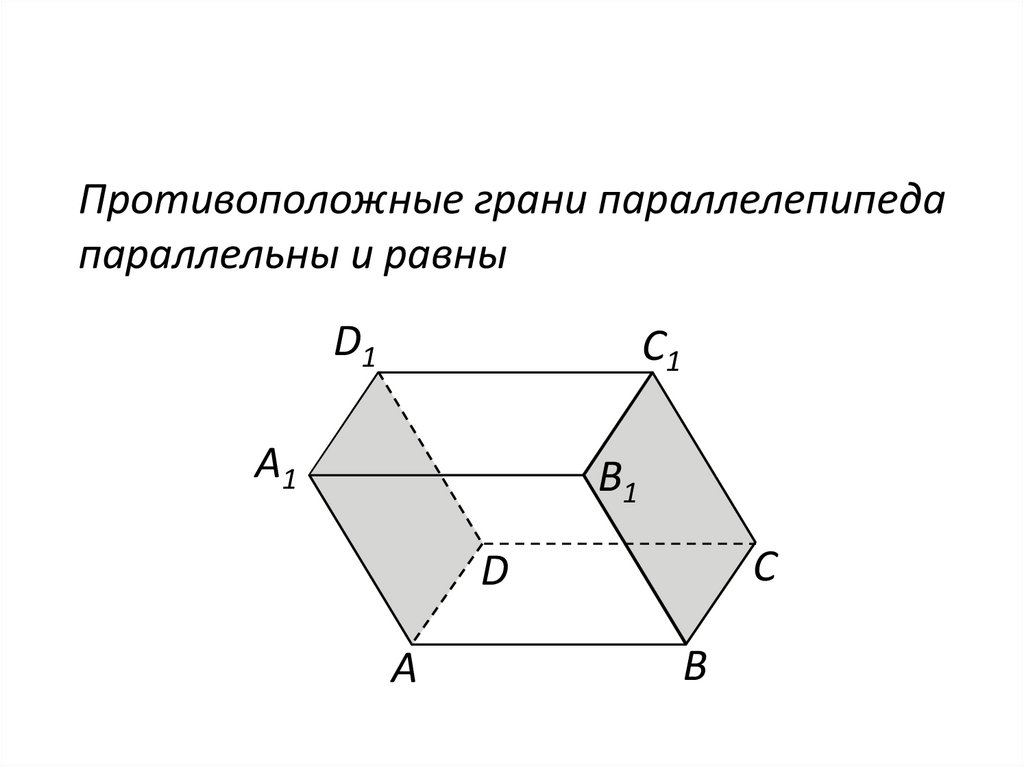
Противоположные грани параллелепипедапараллельны и равны
D1
C1
А1
B1
С
D
А
В
15.
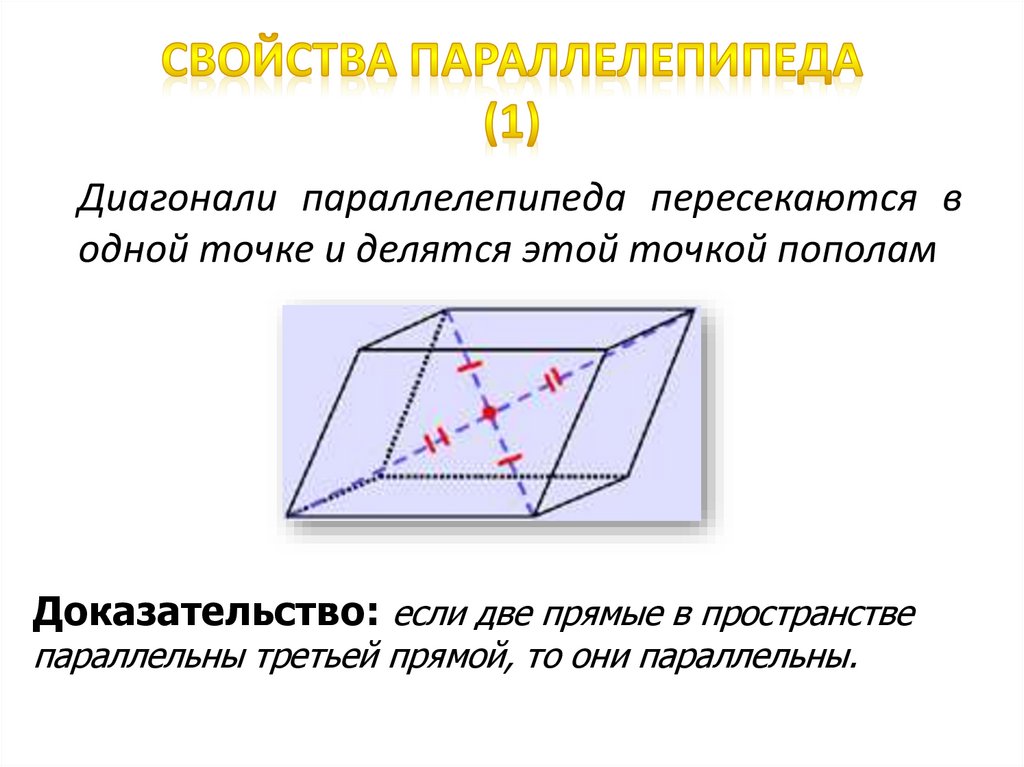
Диагонали параллелепипеда пересекаются водной точке и делятся этой точкой пополам
Доказательство: если две прямые в пространстве
параллельны третьей прямой, то они параллельны.
16.
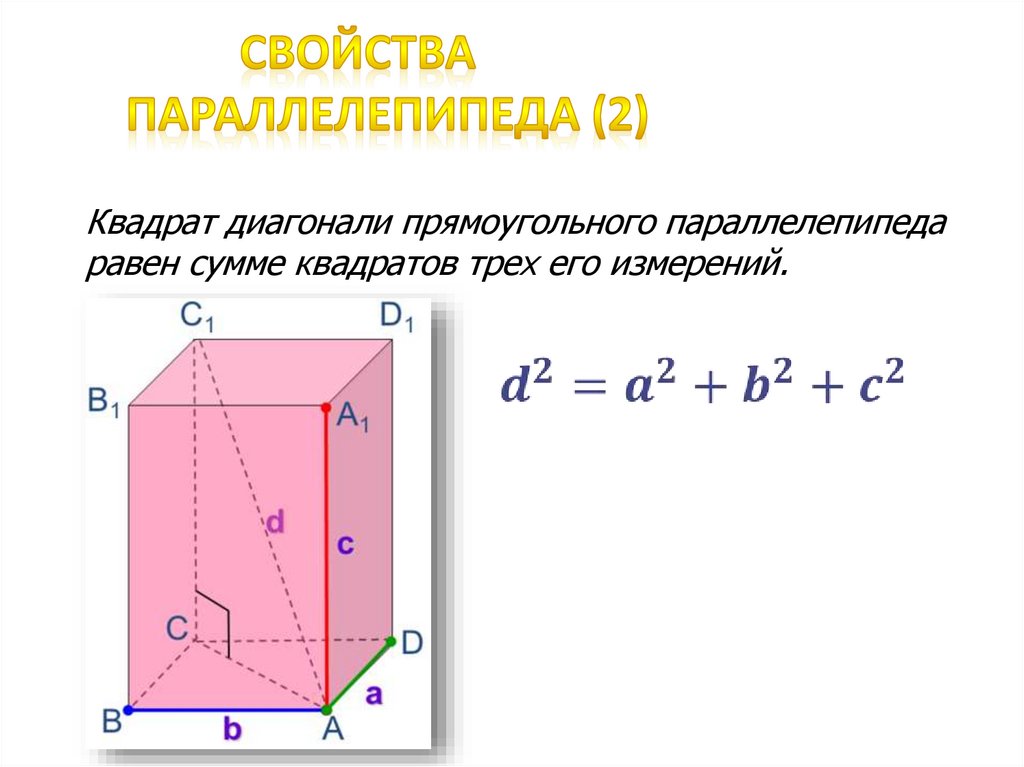
Квадрат диагонали прямоугольного параллелепипедаравен сумме квадратов трех его измерений.
17.
Объем прямоугольного параллелепипеда равенпроизведению трех его измерений.
V=abc
V - объем
a - ширина
b - длина
c - высота
18.
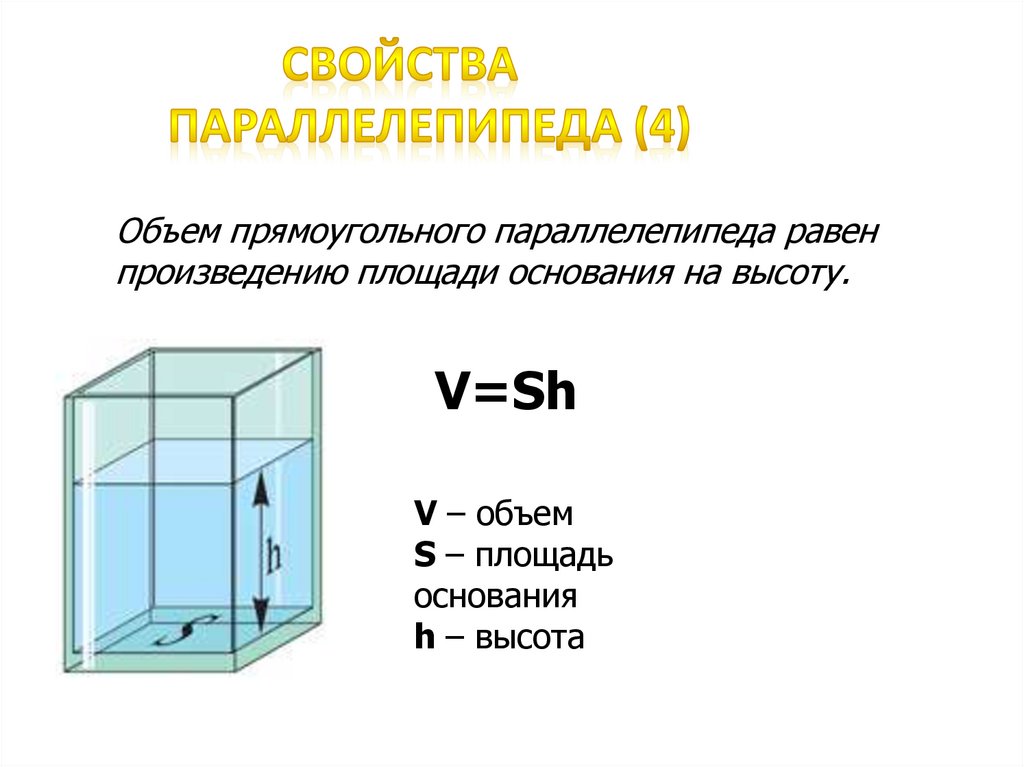
Объем прямоугольного параллелепипеда равенпроизведению площади основания на высоту.
V=Sh
V – объем
S – площадь
основания
h – высота
19.
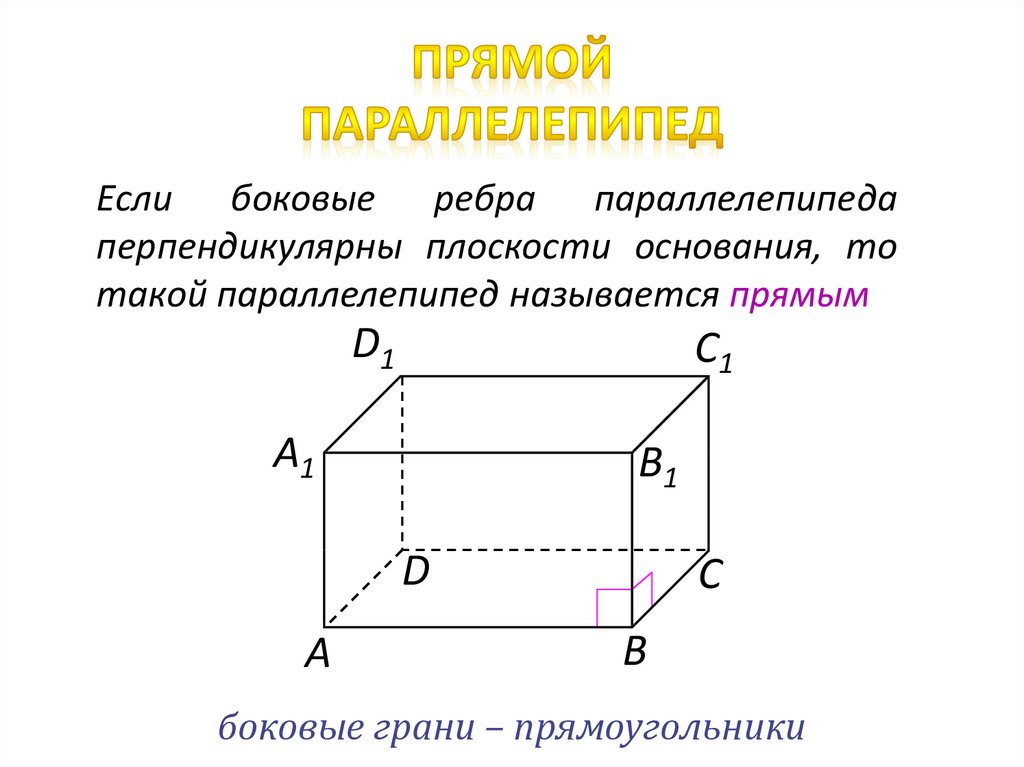
Если боковые ребра параллелепипедаперпендикулярны плоскости основания, то
такой параллелепипед называется прямым
D1
C1
А1
B1
D
А
С
В
боковые грани – прямоугольники
20.
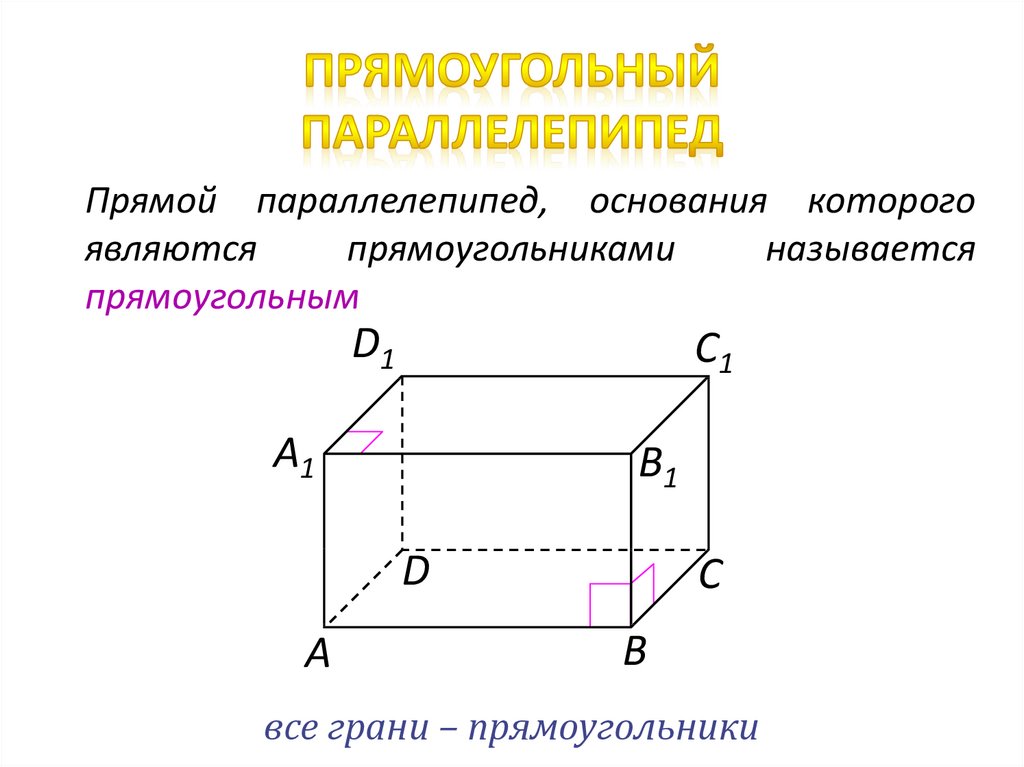
Прямой параллелепипед, основания которогоявляются
прямоугольниками
называется
прямоугольным
D1
C1
А1
B1
D
А
С
В
все грани – прямоугольники
21.
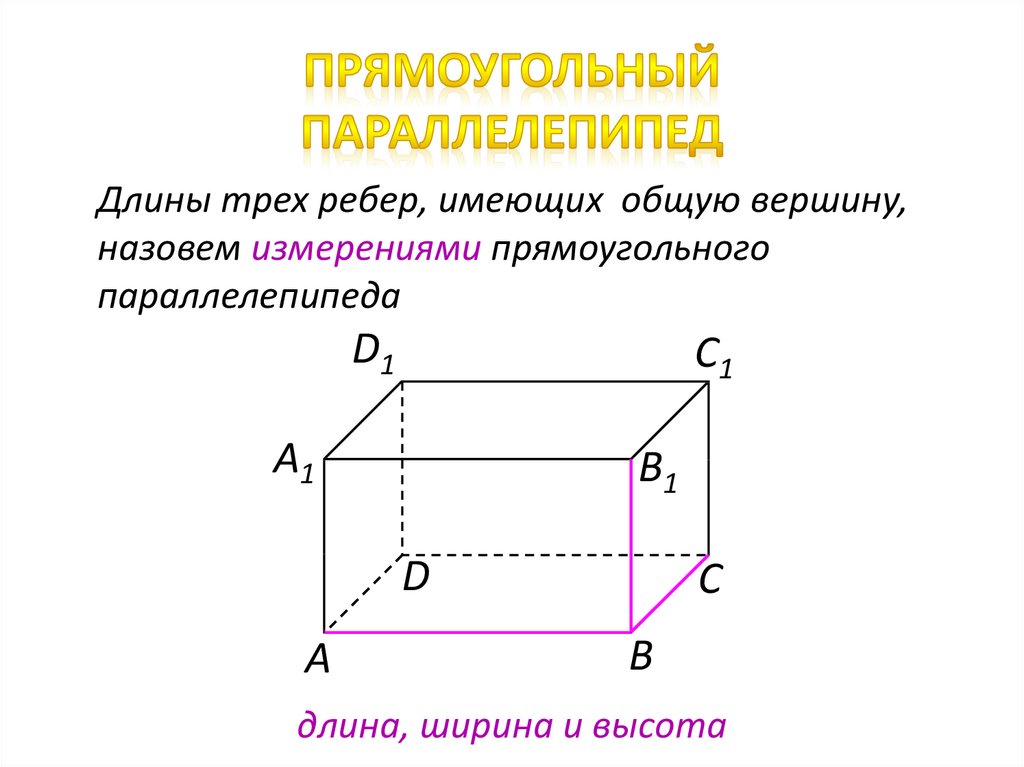
Длины трех ребер, имеющих общую вершину,назовем измерениями прямоугольного
параллелепипеда
D1
C1
А1
B1
D
А
С
В
длина, ширина и высота
22.
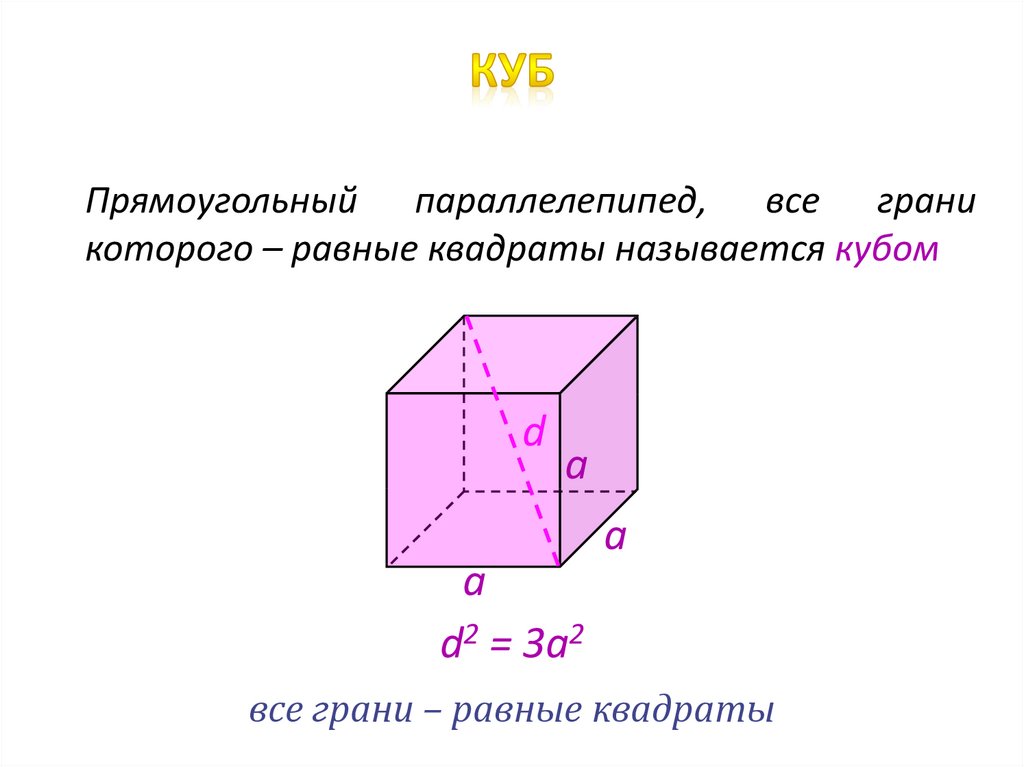
Прямоугольный параллелепипед, все граникоторого – равные квадраты называется кубом
d
a
a
d2 = 3a2
a
все грани – равные квадраты















 Математика
Математика








