Дії з векторами у просторі (правила додавання)

1. Вектори у просторі

2. Операції над векторами

Сума векторів
a a1, a2 , a3 b b1, b2 , b3 c a1 b1, a2 b2 , a3 b3
Правило паралелограма
Правило трикутника
b
a
b
a
c a b
c a b
a і b називається
Сумою векторів
вектор, проведений з початку
першого у кінець другого.
Вектори розташовані
послідовно
a і b є вектор, що
Сумою векторів
збігається з діагоналлю паралелограма,
побудованого на даних векторах .
Вектори виходять з
однієї точки
a
b

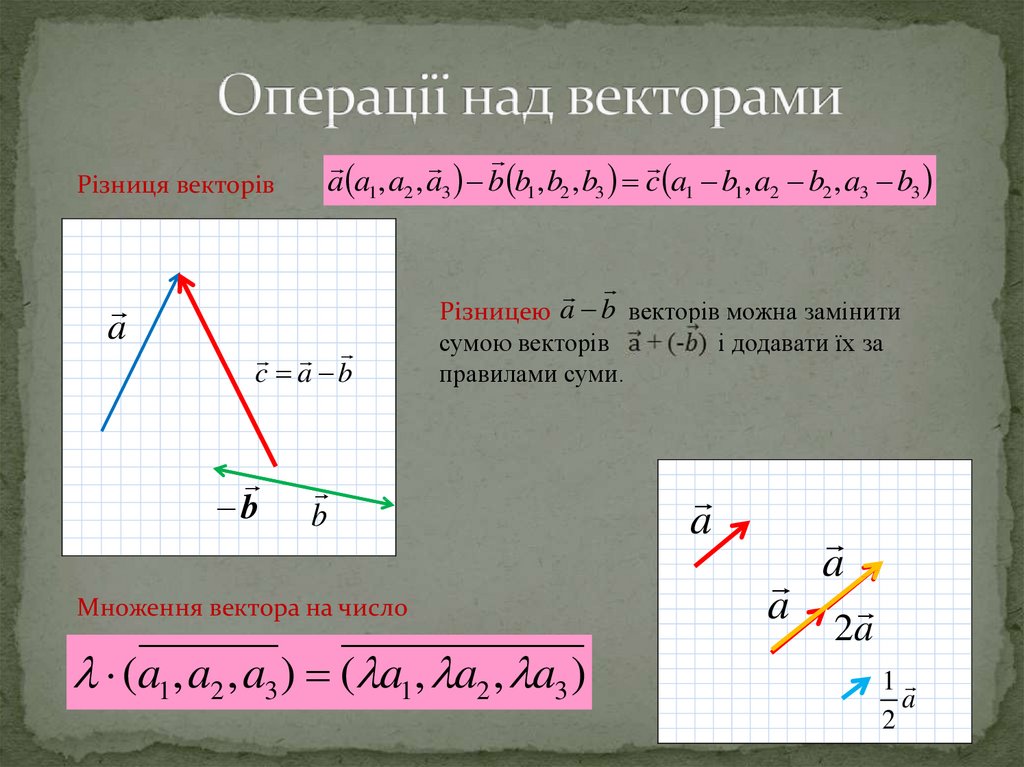
3. Операції над векторами

Різниця векторів
a
a a1, a2 , a3 b b1, b2 , b3 c a1 b1, a2 b2 , a3 b3
Різницею a b векторів можна замінити
c a b
b
сумою векторів
правилами суми.
b
Множення вектора на число
(a1, a2 , a3 ) ( a1, a2 , a3 )
і додавати їх за
a
a
a
2a
1
a
2

4. Умова колінеарності векторів

Вектори колінеарні b a
b1 b2 b3
a1 a2 a3
(відповідні координати пропорційні)
Вектори з координатами (2;4;-6) та (1;2;-3) колінеарні, тому що
2 4 6
1 2 3