Похожие презентации:
Практическая работа «Действия с комплексными числами»
1. Практическая работа «Действия с комплексными числами»
2.
i- комплексное число, такое , чтоi²=-1
z = a+bi – алгебраическая форма записи
комплексного числа
a – действительная часть,
bi – мнимая часть,
i – мнимая единица.
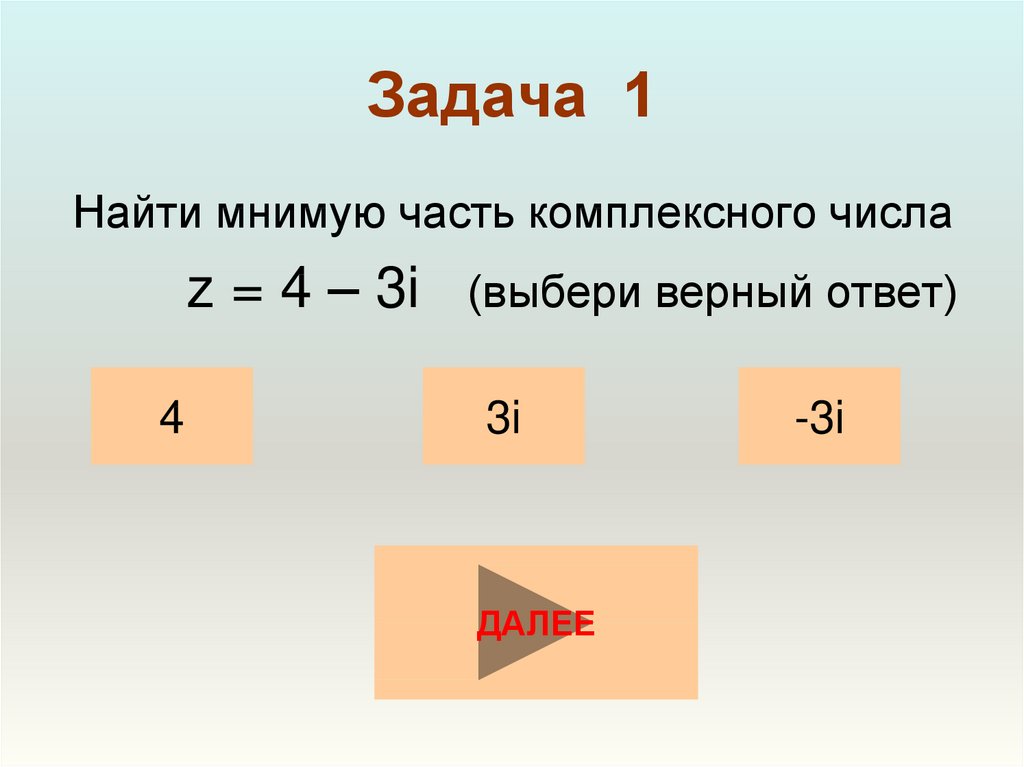
3. Задача 1
Найти мнимую часть комплексного числаz = 4 – 3i (выбери верный ответ)
4
3i
ДАЛЕЕ
-3i
4. Задача 2
Определить вид записи комплексногочисла
z 12 6i
(выбери верный ответ)
алгебраическая
арифметическая
математическая
ДАЛЕЕ
5. Изображение комплексных чисел на координатной плоскости.
6. Задача 3
Определить координаты точки,соответствующей числу z = 3-i
(выбери верный ответ)
(3;0)
(3;-1)
ДАЛЕЕ
(3;1)
7.
• Для вычисления значения степени числа iнеобходимо выполнить следующее:
• показатель степени числа i делим на 4;
• Определить значение степени числа i в
зависимости от полученного остатка
В остатке 0
1
В остатке 1
i
i102 i 4 25 2 i 2 1
i
33
i
4 8 1
i i
1
В остатке 2
-1
В остатке 3
-i
8. Задача 4
Вычислитеi27
(выбери верный ответ)
i
-i
ДАЛЕЕ
-1
9.
• Сложение, вычитание и умножениекомплексных чисел в алгебраической
форе производится по правилам
действия с многочленами:
z1 z 2 (5 4i ) ( 2 3i ) 5 4i 2 3i 3 7i
z1 z 2 (5 4i ) ( 2 3i ) 5 4i 2 3i 7 i
z1 z2 (5 4i) ( 2 3i) 10 15i 8i 12i 2
10 7i 12 22 7i
10. Задача 5
Выполнить вычитаниеz1 3 5i
z1 z 2
z2 6 i
(выбери верный ответ)
z=3–6i
z = -3 +6i
ДАЛЕЕ
z = - 3 +5i
11. Задача 6
Выполнить умножение(1 2i) ( 5i)
(выбери верный ответ)
-10+5i
10-5 i
ДАЛЕЕ
- 10-5i
12. Для нахождения частного двух комплексных чисел необходимо числитель и знаменатель умножить на число, сопряженное знаменателю.
z14 5i
( 4 5i ) ( 2 11i )
z 2 2 11i ( 2 11i ) ( 2 11i )
4 ( 2) 4 11i ( 5i ) ( 2) ( 5i ) 11i
( 2) 11
2
2
8 44i 10i 55i 2 47 54i
47
54
i
4 121
125
125 125
13. Задача 7
z1Найти частное комплексных чисел
z2
z1 1 2i
z2 2 i
(выбери верный ответ)
0,8-0,6i
-i
ДАЛЕЕ
0,8-i
14. Так как , то можно извлекать арифметический квадратный корень из отрицательного числа :
Так как 1 i, то можно
извлекать арифметический
квадратный корень из
отрицательного числа :
36 36 ( 1) 36 1 6i
1
1
1
1
( 1)
1 i
4
4
4
2
17 17 ( 1) 17 1 17i
15. Задача 8
Вычислить64
(выбери верный ответ)
±8i
8i
ДАЛЕЕ
-8
16. Модулем комплексного числа z=a+bi называется длина вектора, соответствующего этому числу.
Обозначение:r,|z|Формула:
r z a b .
2
2
17. Задача 9
Вычислить модуль числаz 4 3i
(выбери верный ответ)
7
5
ДАЛЕЕ
1
18. Аргументом комплексного числа z≠0 называется угол , который образует вектор z с положительным направлением оси абсцисс.
Аргументом комплексного числа z≠0называется угол , который образует
вектор z с положительным
направлением оси абсцисс.
• Обозначение:
, arg(z).
a
cos ,
r
b
sin .
r
19. Задача 10
Вычислить аргумент z = -3π
π/2
ДАЛЕЕ
0
20.
z r(cos i sin )• Тригонометрическая форма записи
комплексного числа
z re
i
• Показательная форма записи
комплексного числа
21. Задача 11
Определить форму записи комплексногочисла ( выбери верный ответ)
z
7
i
12
3e
тригонометрическая
показательная
алгебраическая
ДАЛЕЕ
22. Задача 12
Записать число Z = - 4показательной форме
z 4e i
z 4e i
ДАЛЕЕ
в
z 2e i
23. Задача 13
Определить аргументкомплексного числа
z 16(cos i sin )
12
12
12
16
ДАЛЕЕ
4
24.
далеедалее
25.
НЕВЕРНО!ПОПРОБУЙ
ЕЩЁ РАЗ!


























 Математика
Математика








