Похожие презентации:
Теория принятия решений. Матричные игры, пример решения
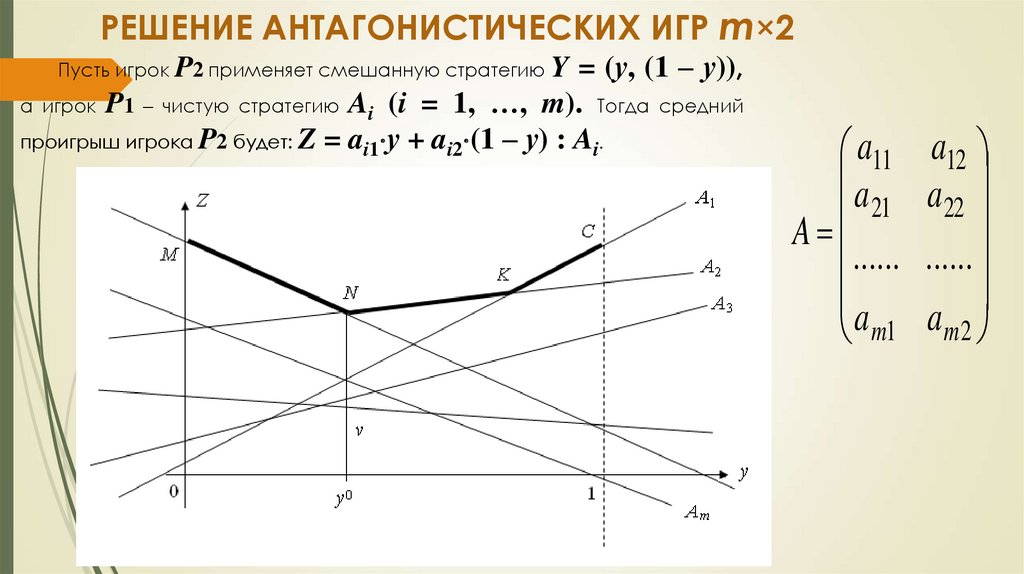
1. РЕШЕНИЕ АНТАГОНИСТИЧЕСКИХ ИГР m×2
= (у, (1 – у)),а игрок P1 – чистую стратегию Ai (i = 1, …, m). Тогда средний
проигрыш игрока P2 будет: Z = ai1 у + ai2 (1 – у) : Ai.
Пусть игрок P2 применяет смешанную стратегию Y
a11
a
21
A
......
a m1
a12
a 22
......
a m2
2.
В качестве активных стратегий игрока P1 можно выбрать двечистых стратегии, соответствующие прямым, пересекающимся в N.
Пусть это Ai и Aj.
ai1 ai 2
A*
a
a
j2
j1
Оптимальную смешанную стратегию игрока P1: X0 = (х0, (1 – х0))
можно определить как для игры 2 2
ai1 x a j1 (1 x) V
ai 2 x a j 2 (1 x) V
Х0 = (0, …, 0, х0, 0, …, 0, 1 – х0, 0, …, 0)
i-я компонента
j-я компонента
3. ПРИМЕР 9
В точке N пересекаются прямыеА1 :
4y + 3 (1 – y) = Z
А1 и А4
A2 :
2y + 4 (1 – y) = Z
A3 :
5 (1 – y) = Z
4y + 3 (1 – y) = –y + 6 (1 – y)
y0 = 3/8, Y 0 = (3/8, 5/8)
A4 :
–y + 6 (1 – y) = Z
V = 27/8
В1 : 4x0 – (1 – x0) = V
4 3
A*
1 6
В2 : 3x0 + 6 (1 – x0) = V
4x0 – (1 – x0) = 3x* + 6 (1 – x0)
x0 = 7/8, 1 – x0 = 1/8
Х 0 = (7/8, 0, 0, 1/8)
4
2
A
0
1
3
4
5
6
4. РЕШЕНИЕ АНТАГОНИСТИЧЕСКИХ ИГР 2×n
Пусть игрок P1 применяет смешанную стратегию (х,а игрок P2 – активную стратегию Bj
1–х),
(j = 1, …, n).
Вi : Z = a1ix + a2i (1 – x)
Какую бы стратегию ни применил игрок
P2,
игрок
a11
A
P1
a 21
получит выигрыш не менее ординаты ломаной линии MNKC.
a12
a 22
... a1n
... a 2 n
5.
Оптимальная стратегия игрока P1: Х0 = (x0, (1 – x0))Цена игры V равна ординате точки К
В качестве активных стратегий игрока P2 можно выбрать две чистых
стратегии, соответствующих любым двум прямым, пересекающимся в
точке К. Пусть это Вi и Вj
a1i
A*
a 2i
a1 j
a 2 j
Оптимальную смешанную стратегию игрока
P2 найти как в игре 2 2
a1i y a1 j (1 y) Z
a2i y a2 j (1 y) Z
Y 0 = (0, …, 0, у0, 0, …, 0, 1 – у0, 0, …, 0)
i-я компонента
j-я компонента
6.
ПРИМЕР 10В1 :2x + 4 (1 – x) = Z
В2 :3x + 2 (1 – x) = Z
2 3 1 4
A
4 2 3 1
В точке N пересекаются прямые В3 и В4,
x + 3 (1 – x) = 4x + (1 – x)
В3 :x + 3 (1 – x) = Z
В4 :4x + (1 – x) = Z
1 4
A*
3 1
x0 = 2/5, Х 0 = (2/5, 3/5)
V = 11/5
Активными стратегиями игрока P2 будут В3 и В4,
А1 :y + 4 (1 – y) = Z
A2 : 3y + (1 – y) = Z
y0 = 3/5
Y 0 = (0, 0, 3/5, 2/5)
7.
1 4 6 xA
9 5 3 1 x
ПРИМЕР 11
Z x 9 1 x 9 8 x,
Z 4 x 5 1 x 5 x,
Z 6 x 3 1 x 3 3x.
1
5 x 3 3 x x , V 4,5
2
0
1 1
X ,
2 2
0
Активными стратегиями второго игрока являются вторая и
третья стратегии
4 6
5 3
Y 0, 3 , 1
4 4
0






 Математика
Математика








