Массоперенос в аналитической химии

1.

Массоперенос в аналитической
химии
1

2.

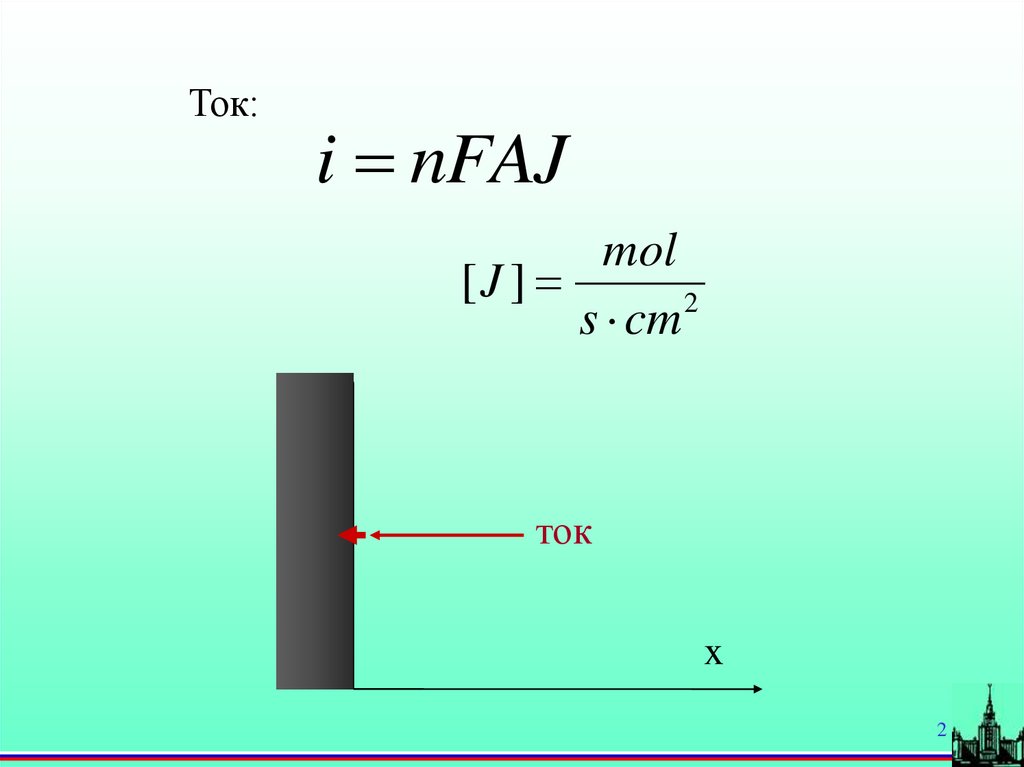
Ток:
i nFAJ
mol
[J ]
2
s cm
ток
x
2

3. Adolf Fick

Диффузионные законы Adolf Fick
(1885)
C ( x, t )
J ( x, t ) D
x
cm
[ D]
s
(1829-1901)
2
3

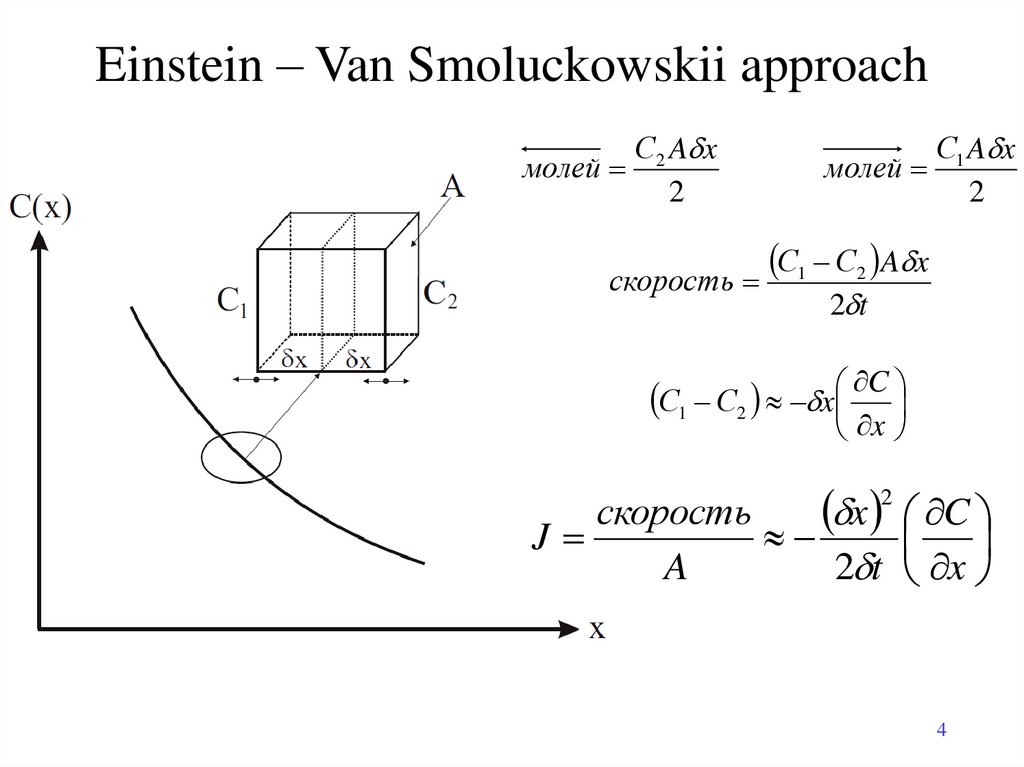
4. Einstein – Van Smoluckowskii approach

молей
С2 A x
2
молей
С1 A x
2
С1 С2 A x
скорость
2 t
C
С1 С2 x
x
скорость
x C
J
A
2 t x
2
4

5. Einstein – Van Smoluckowskii approach

скорость
x C
J
A
2 t x
2
C
J D
x
x 2
D
2 t
x 2 2Dt
5

6. II диффузионный закон

молей n J ( x) J ( x x) A t
Тейлор:
J
n x A t
x
J
J ( x x ) J ( x ) x
x
n
C
A x
C C
J
2C
D 2
t
t
x
x
6

7. II диффузионный закон

C
2C
D 2
t
x
2C 2C 2C
C
D 2 2 2
t
y
z
x
Одномерный вариант
C
D 2 C
t
7

8.

Общие уравнения
массопереноса
Конвекция:
J Ci
c
i
Массоперенос без конвекции:
DiCi
e
J i
grad i
RT
8

9.

Общие уравнения
массопереноса
Электрохимический потенциал:
RT ln ai zi F
e
i
o
i
Безконвекционный массоперенос:
zi FDiCi
J i DiCi grad (ln ai )
grad
RT
для разбавленных растворов:
zi FDiCi
J i Di grad Ci
grad
RT
9

10.

Общие уравнения
массопереноса
Уравнение Нернста-Планка:
zi FDiCi
J Ci Di grad Ci
grad
RT
i
конвекция диффузия
миграция
10

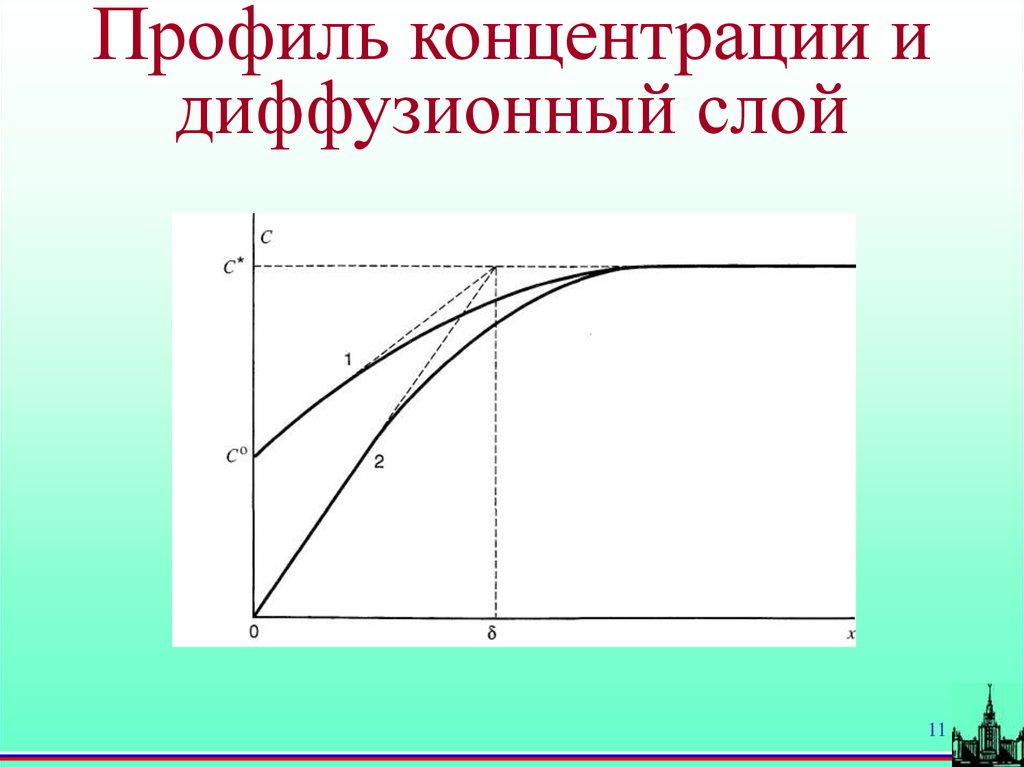
11.

Профиль концентрации и
диффузионный слой
11

12.

Полуэмпирическое решение
нестационарной реакции
i
C ( x)
J ( x 0) D
x x 0 nFA
o
C
(
x
)
C
*
C
x 0 x
i
D
o
[C * C ]
nFA
C*
Co
x
δ
12

13.

Предельный диффузионный
ток
C*
m
D
C 0
o
il nFA m C *
x
δ
13

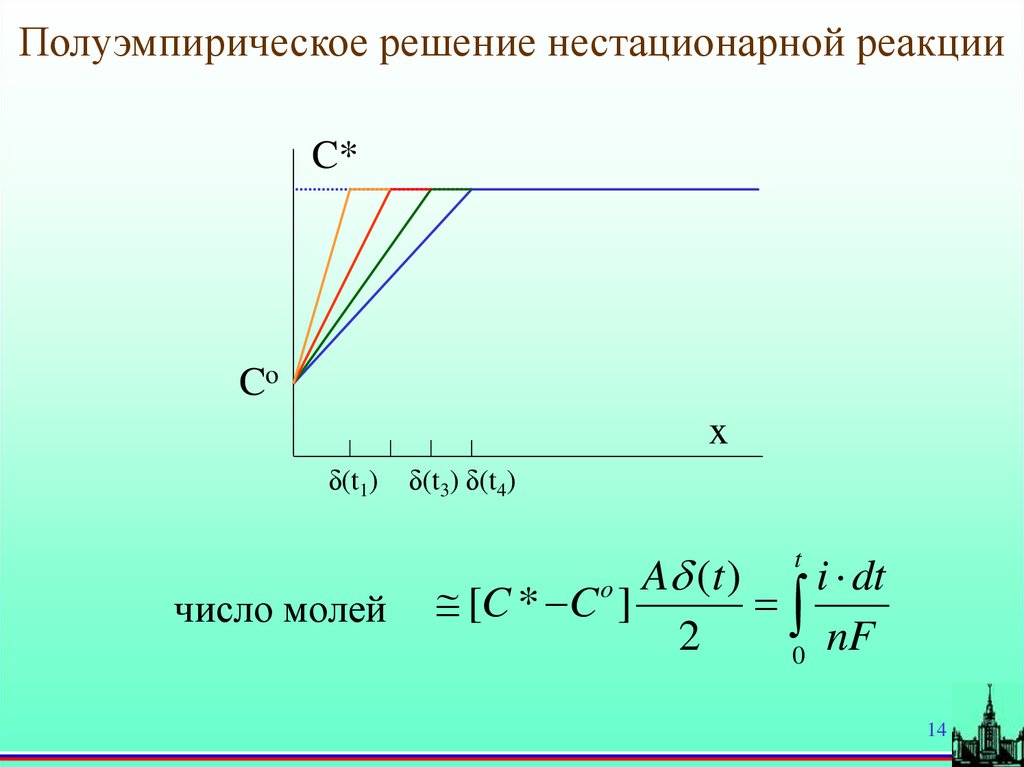
14.

Полуэмпирическое решение нестационарной реакции
C*
Co
x
δ(t1)
δ(t3) δ(t4)
A (t )
i dt
[C * C ]
2
nF
0
t
число молей
o
14

15.

Полуэмпирическое решение нестационарной реакции
A (t )
i dt
[C * C ]
2
nF
0
t
o
i
D
[C * C o ]
nFA
[C * C o ] A d (t )
i
DA
[C * C o ]
2
dt
nF (t )
d (t ) 2 D
dt
(t )
(t ) 2 Dt
15

16.

Полуэмпирическое решение нестационарной реакции
i
D1/ 2
1/ 2 [C * C o ]
nFA 2t
Диффузионно-контролируемый процесс: C (0, t ) 0
1/ 2
i
D
1/ 2 C
nFA 2t
Уравнение Котрелла:
1/ 2
i (t )
D
1/ 2 1/ 2 C
nFA t
16

17.

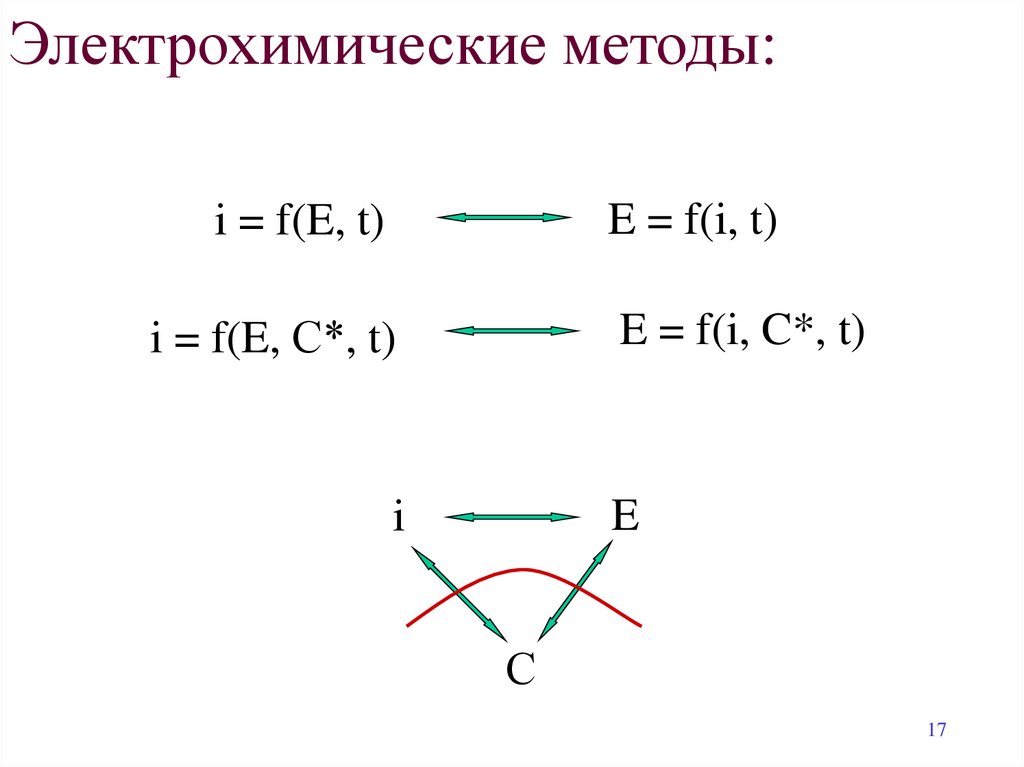
Электрохимические методы:
E = f(i, t)
i = f(E, t)
i = f(E, С*, t)
E = f(i, C*, t)
E
i
С
17

18.

Диффузионные законы
C ( x, t )
J ( x, t ) D
x
C ( x, t )
C ( x, t )
D
2
t
x
2
18

19.

Скачок потенциала – Cottrell equation (1902)
C
2C
D 2
t
x
t = 0: C(x) = C*
t > 0: C(0) = 0
C(x→∞) = C*
подстановка
d 2C
dC
2Г
0
2
dГ
dГ
x
Г
2 Dt
dC
a exp Г 2
dГ
19

20.

Уравнение Котрелла:
dC
a exp Г 2
dГ
x
С С erf
2 Dt
С учетом граничных условий:
i nFAJ x 0
*
J
x 0
nFA DC
i
t
C
D
x
x 0
*
20

21.

Миниатюризация
диффузия
21

22.

Cottrell equation:
1/ 2
1/ 2
it
nFD
2
r C
1/ 2
1/ 2
Dt
2.12 2
r
[1
]
P.J. Lingane. Anal. Chem. 36 (1964) 1723
Ultramicroelectrode:
i lim( i )r 0 4nFDCr
K. Aoki. Electroanalysis 5 (1993) 627-39
22

23.

Стационарный ток
микроэлектродов
Сферический:
I ss 4 nFDCr
Полусферический:
I ss 2 nFDCr
Дисковый:
I ss 4nFDCr
23

24.

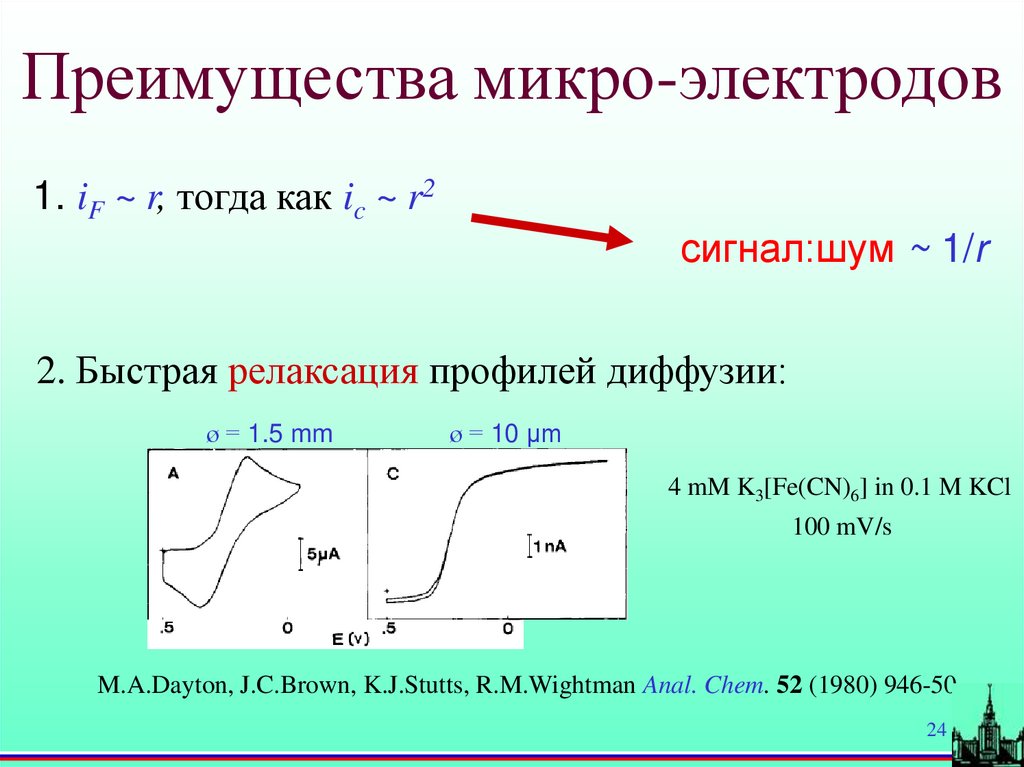
Преимущества микро-электродов
1. iF ~ r, тогда как ic ~ r2
сигнал:шум ~ 1/r
2. Быстрая релаксация профилей диффузии:
ø = 1.5 mm
ø = 10 µm
4 mM K3[Fe(CN)6] in 0.1 M KCl
100 mV/s
M.A.Dayton, J.C.Brown, K.J.Stutts, R.M.Wightman Anal. Chem. 52 (1980) 946-50
24

25.

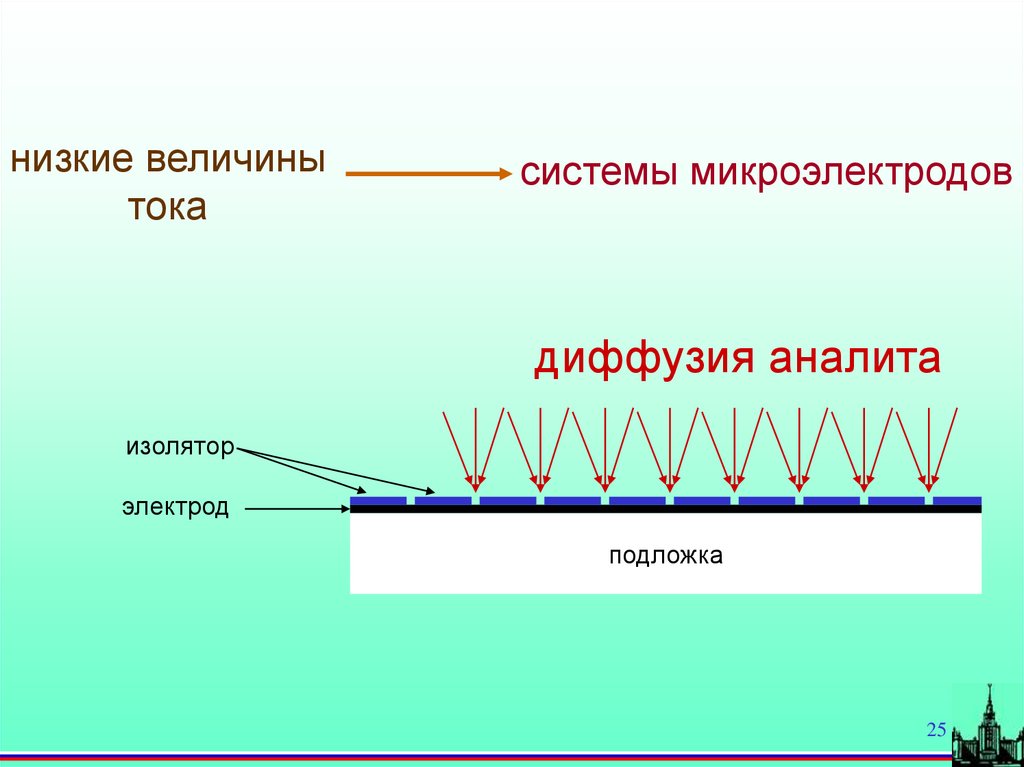
низкие величины
тока
системы микроэлектродов
диффузия аналита
изолятор
электрод
подложка
25

26.

26

27.

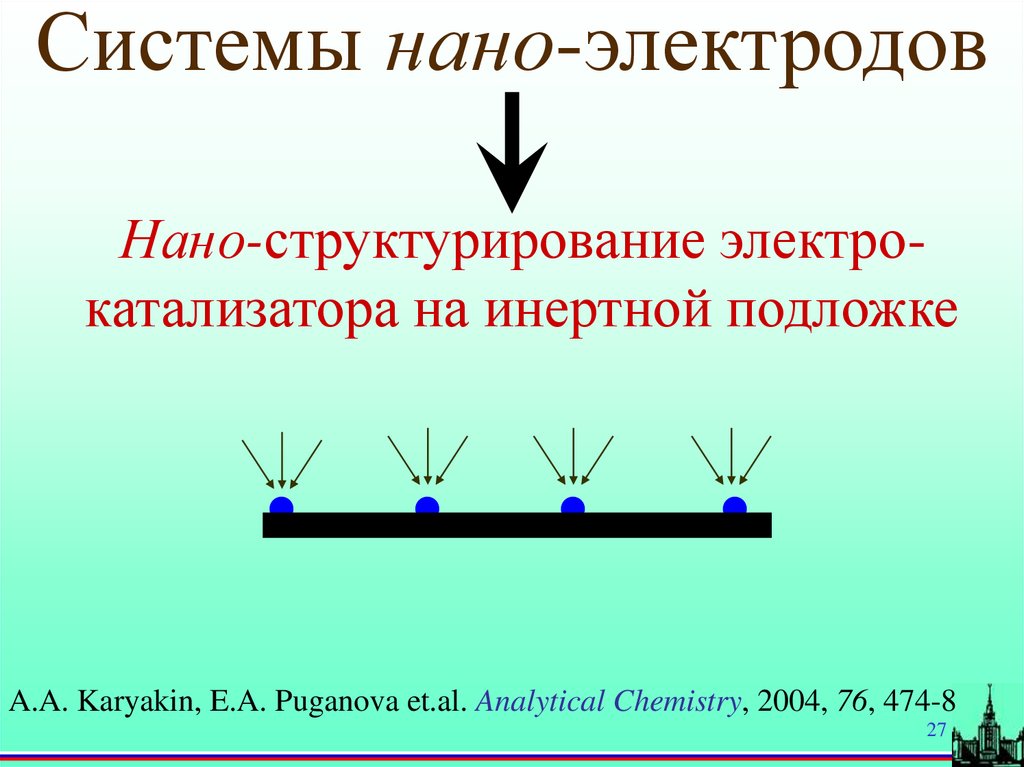
Системы нано-электродов
Нано-структурирование электрокатализатора на инертной подложке
A.A. Karyakin, E.A. Puganova et.al. Analytical Chemistry, 2004, 76, 474-8
27

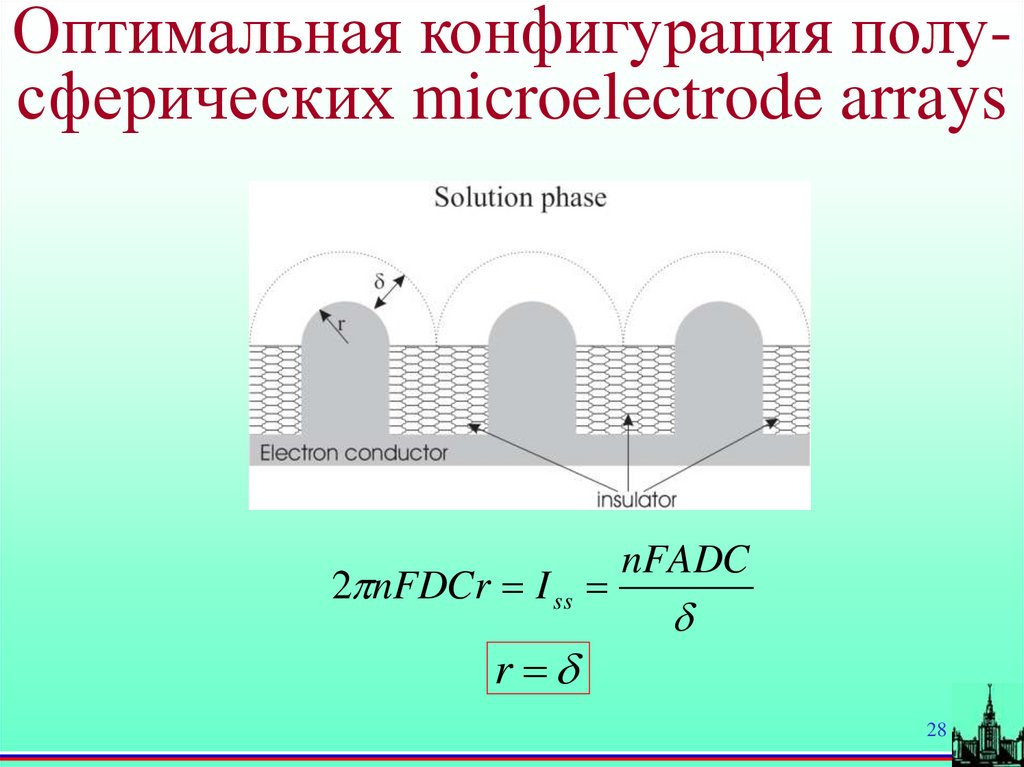
28.

Оптимальная конфигурация полусферических microelectrode arrays
2 nFDCr I ss
r
nFADC
28

29.

АСМ-изображения Берлинской лазури
обычная
нано-структурированная
жидкие кристаллы
золь алкоксисиланов
нуклеация роста
29

30.

10
-2
10
-4
10
-6
15
i, nA cm
-2
i, A cm
-2
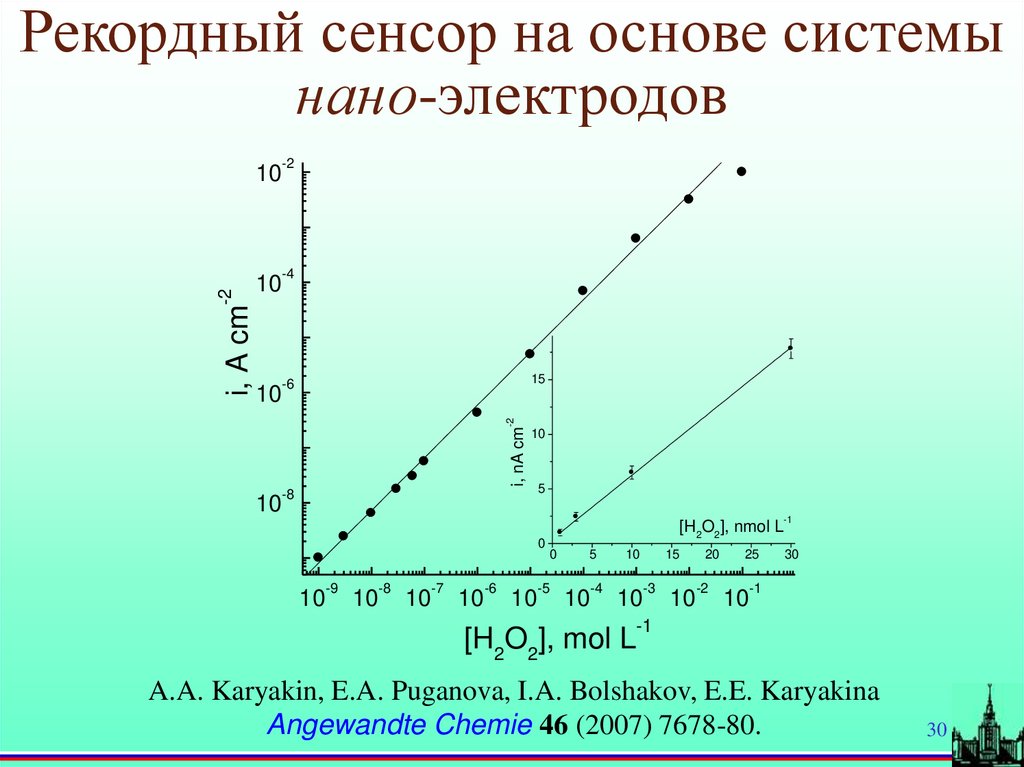
Рекордный сенсор на основе системы
нано-электродов
10
10
-8
5
-1
0
10
-9
10
-8
10
-7
10
-6
10
[H2O2], nmol L
0
-5
5
10
-4
10
10
[H2O2], mol L
15
-3
10
20
-2
25
10
30
-1
-1
A.A. Karyakin, E.A. Puganova, I.A. Bolshakov, E.E. Karyakina
Angewandte Chemie 46 (2007) 7678-80.
30

31.

Гидродинамика
Вращающийся дисковый электрод
Уравнение Левича:
ω
il 0.620nFAD
2/3
C
1 / 6
1/ 2
31

32.

Гидродинамика
Вращающийся дисковый электрод
Уравнение Левича:
i 0.620nFAD2 / 3 1 / 6 1 / 2C
D
i nFA C
1.61D
1/ 3 1/ 6
1 / 2
C*
Co
x
δ
32

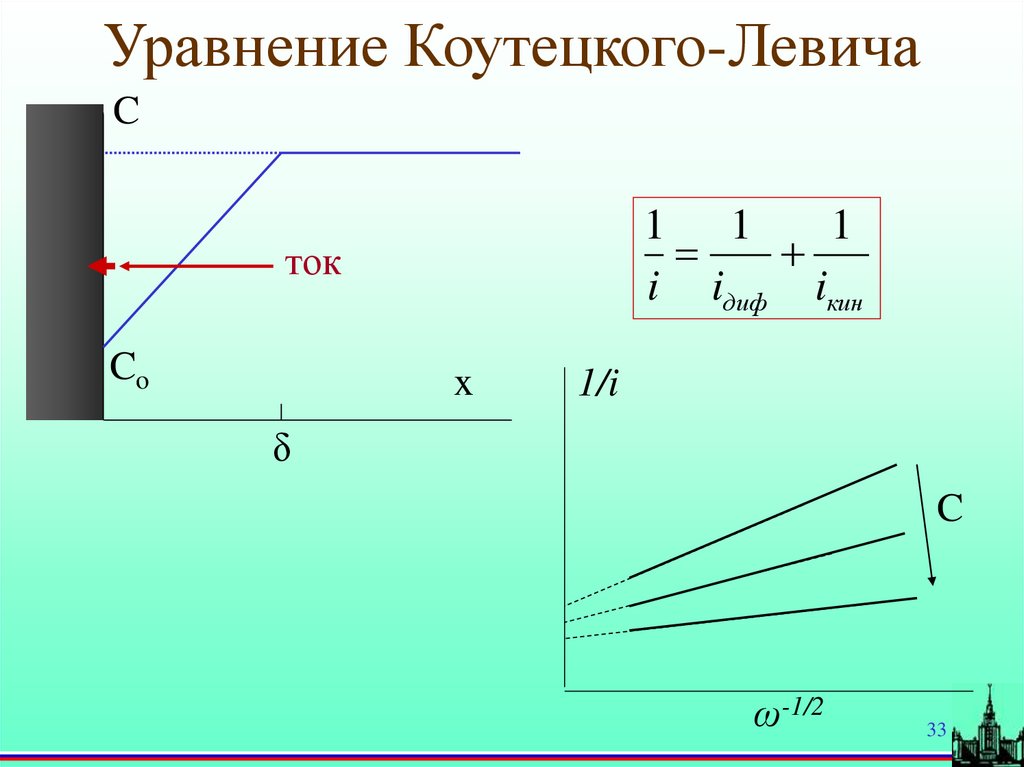
33.

Уравнение Коутецкого-Левича
C
1 1
1
i iдиф iкин
ток
Co
x
1/i
δ
C
ω-1/2
33

34.

Детекторы
Жидкостная хроматография
Проточно-инжекционный
анализ
• тонкослойные;
• wall-jet.
34

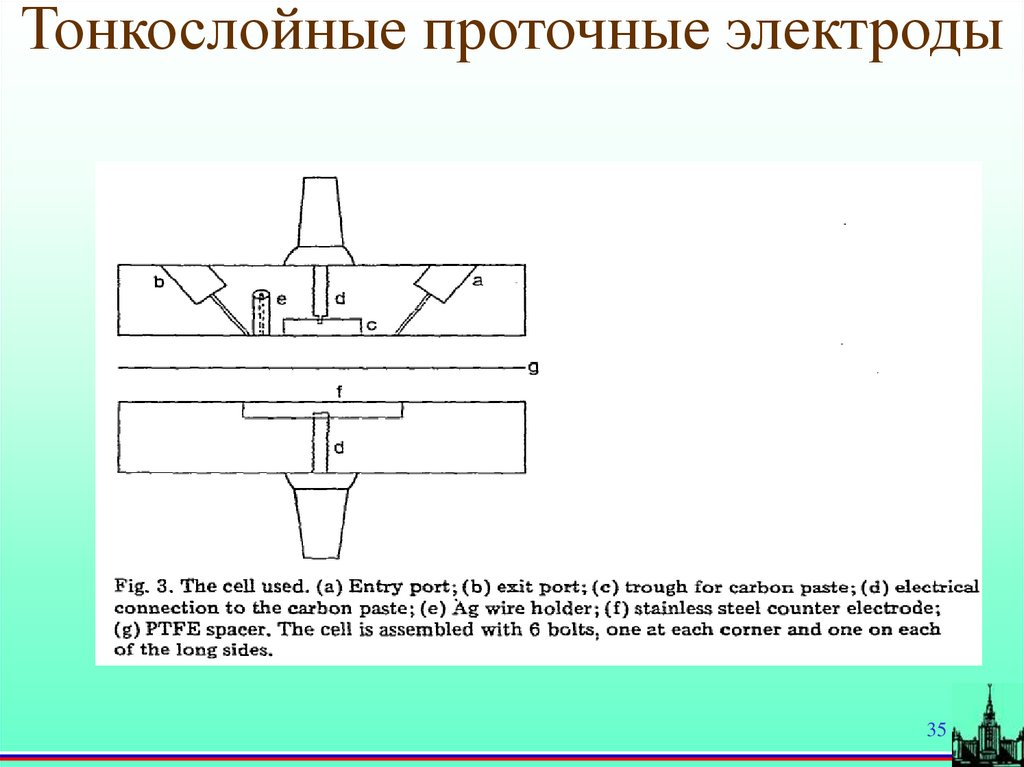
35.

Тонкослойные проточные электроды
35

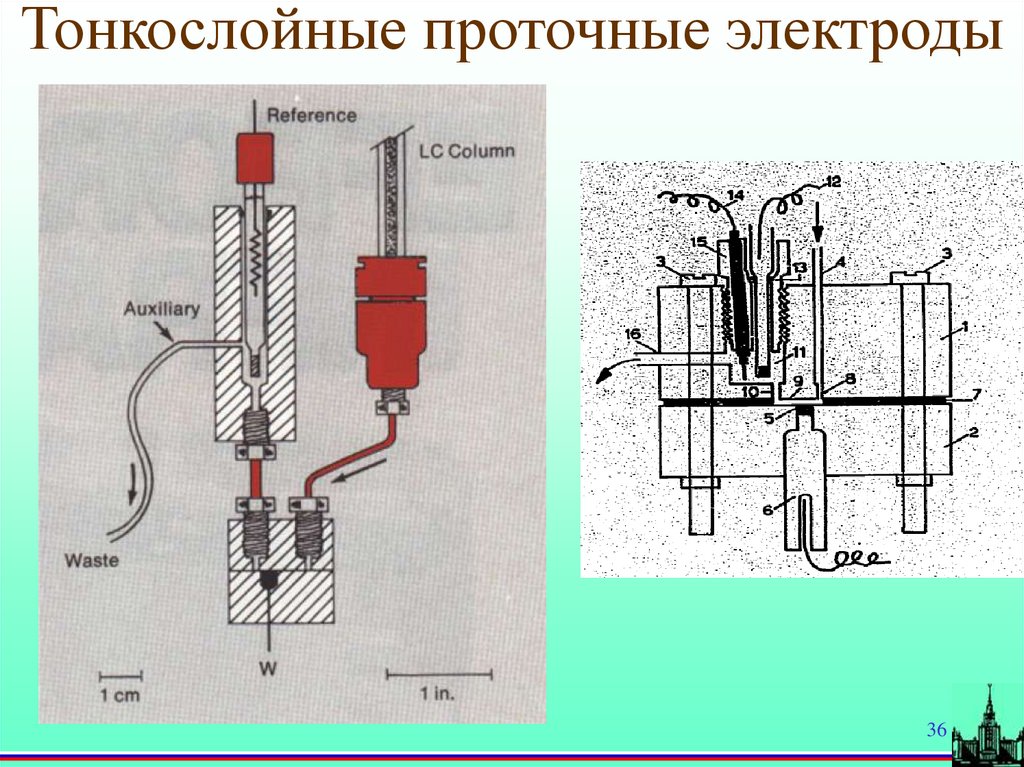
36.

Тонкослойные проточные электроды
36

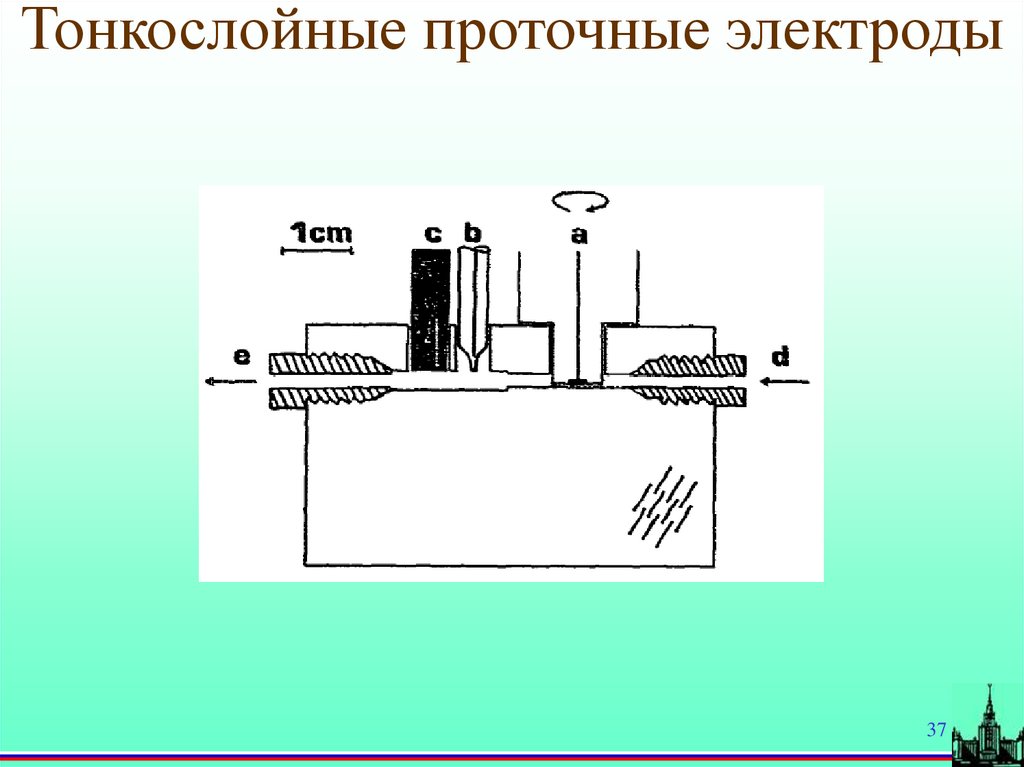
37.

Тонкослойные проточные электроды
37

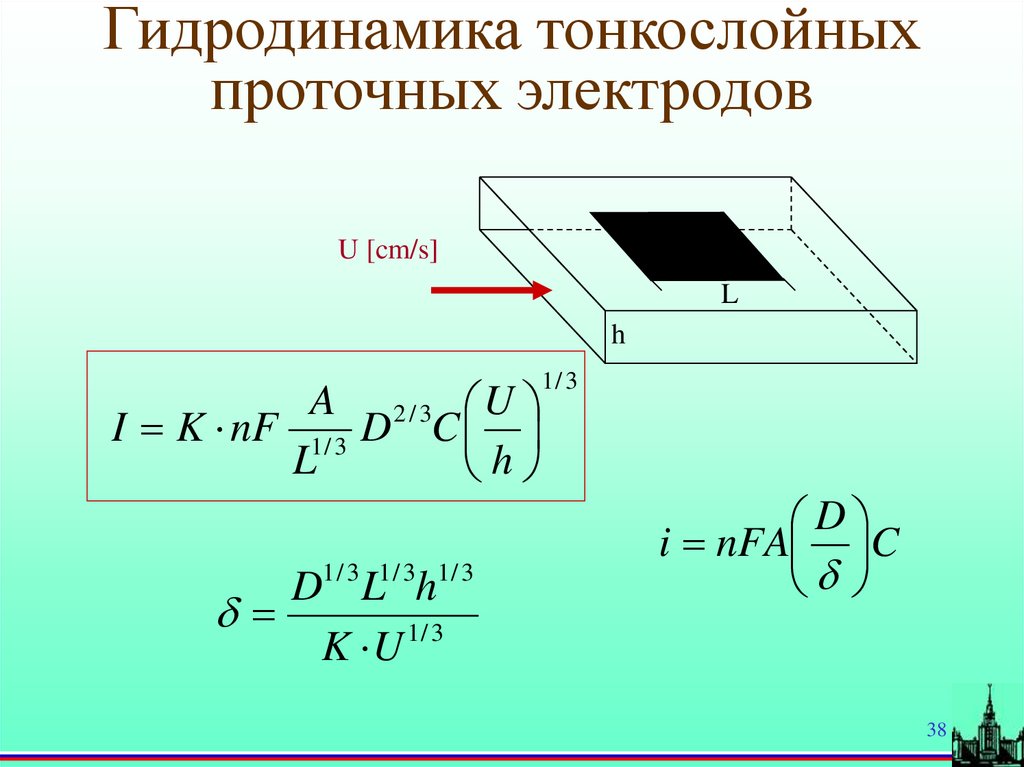
38.

Гидродинамика тонкослойных
проточных электродов
U [cm/s]
L
h
1/ 3
A 2/3 U
I K nF 1 / 3 D C
L
h
1/ 3 1/ 3 1/ 3
D L h
K U 1/ 3
D
i nFA C
38

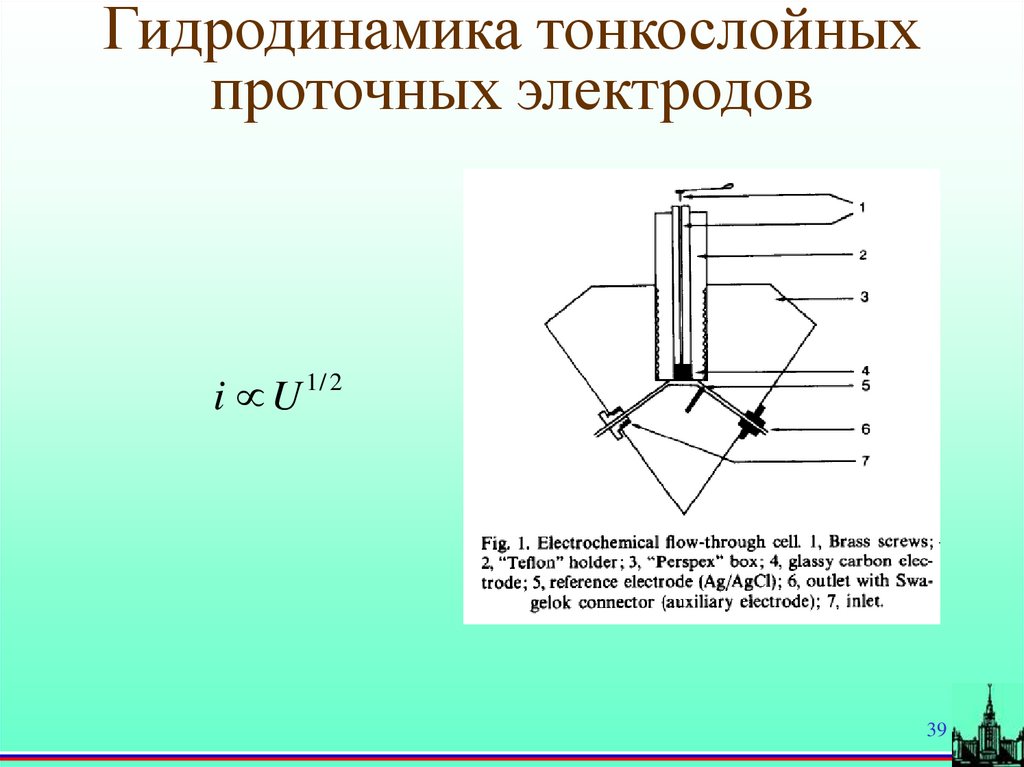
39.

Гидродинамика тонкослойных
проточных электродов
i U 1/ 2
39

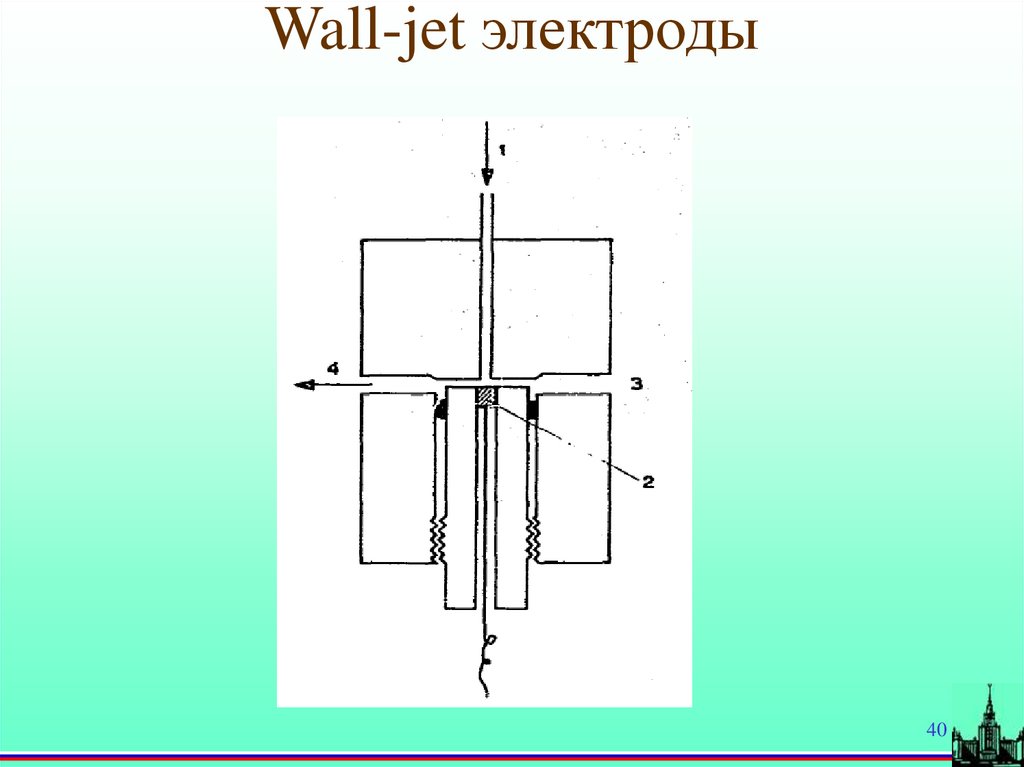
40.

Wall-jet электроды
40

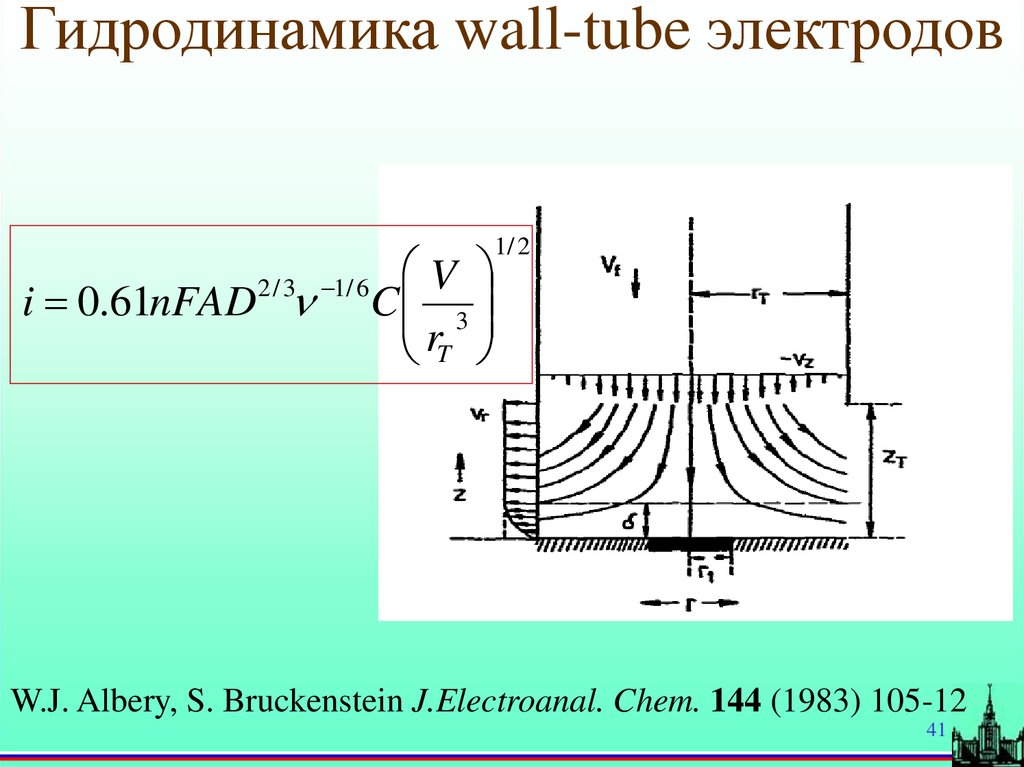
41.

Гидродинамика wall-tube электродов
1/ 2
i 0.61nFAD
2 / 3 1/ 6
V
C 3
rT
W.J. Albery, S. Bruckenstein J.Electroanal. Chem. 144 (1983) 105-12
41

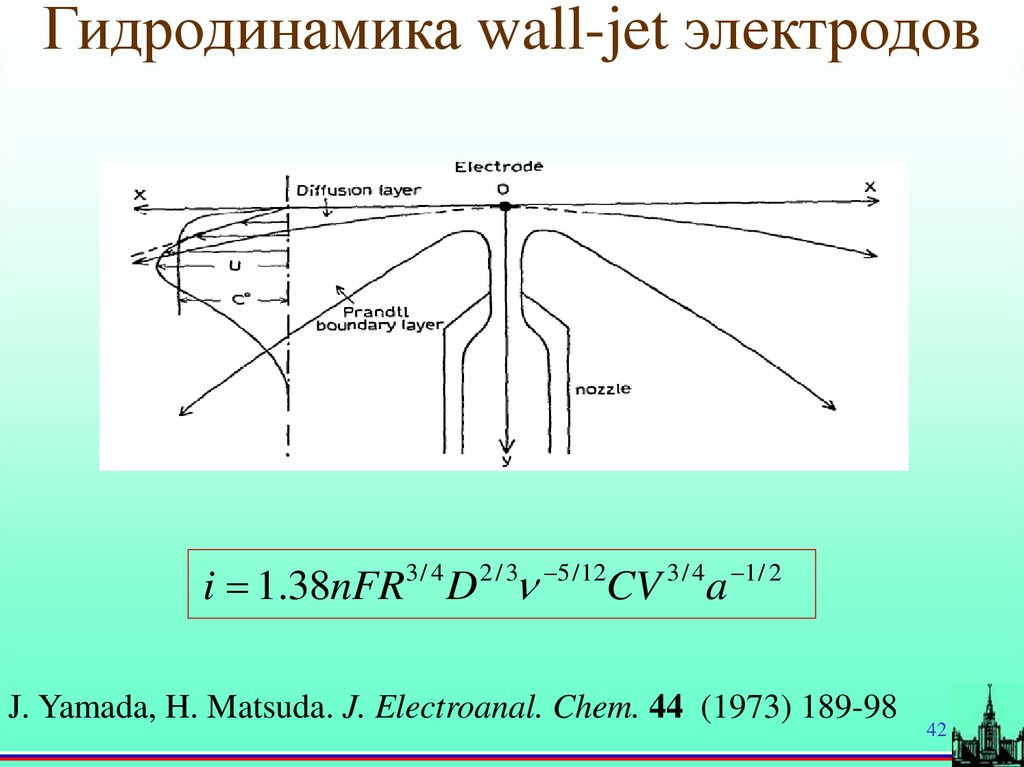
42.

Гидродинамика wall-jet электродов
i 1.38nFR D
3/ 4
2/3
5 / 12
CV
3/ 4
a
1 / 2
J. Yamada, H. Matsuda. J. Electroanal. Chem. 44 (1973) 189-98
42

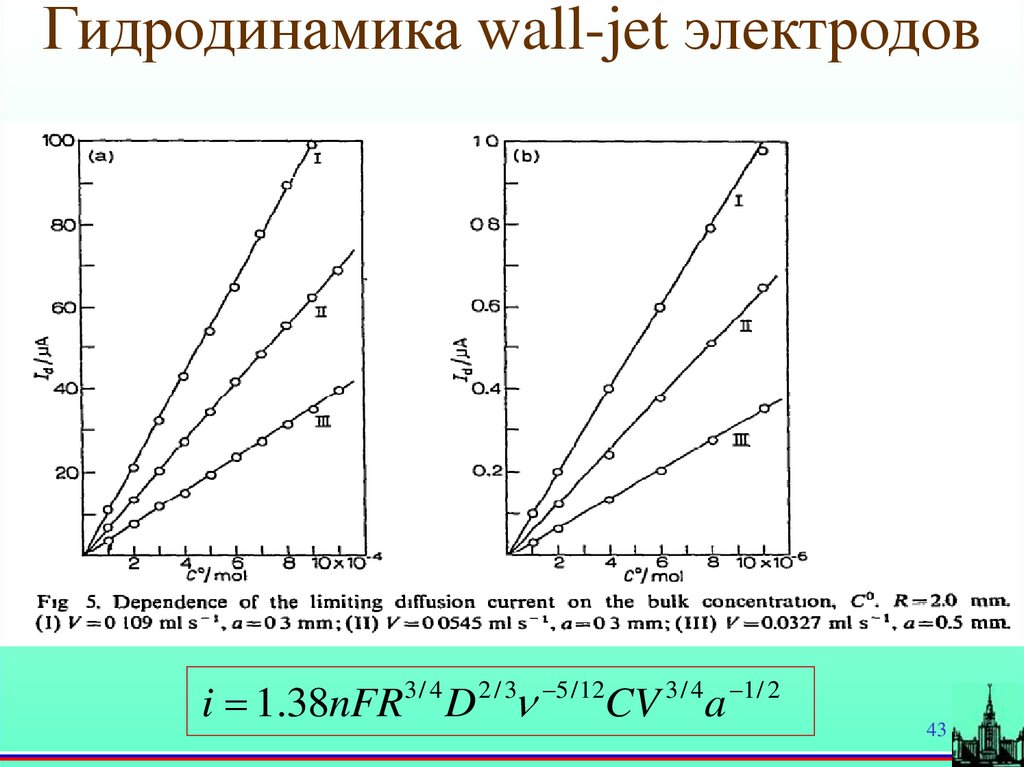
43.

Гидродинамика wall-jet электродов
i 1.38nFR3 / 4 D 2 / 3 5 / 12CV 3 / 4a 1 / 2
43

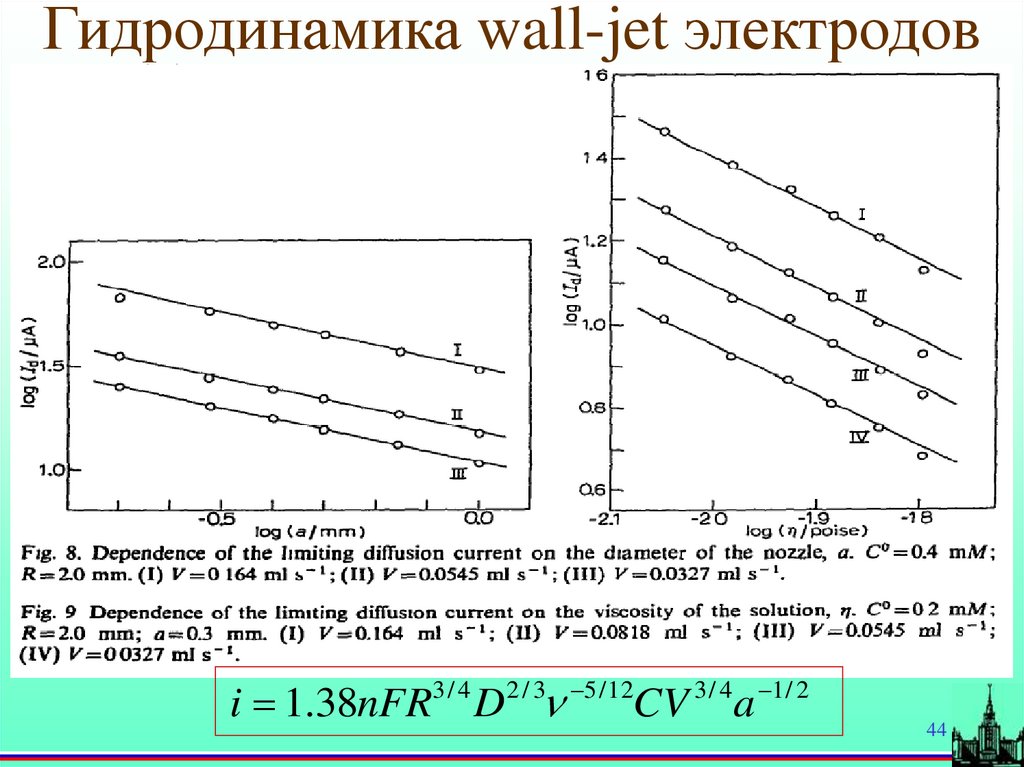
44.

Гидродинамика wall-jet электродов
i 1.38nFR3 / 4 D 2 / 3 5 / 12CV 3 / 4a 1 / 2
44

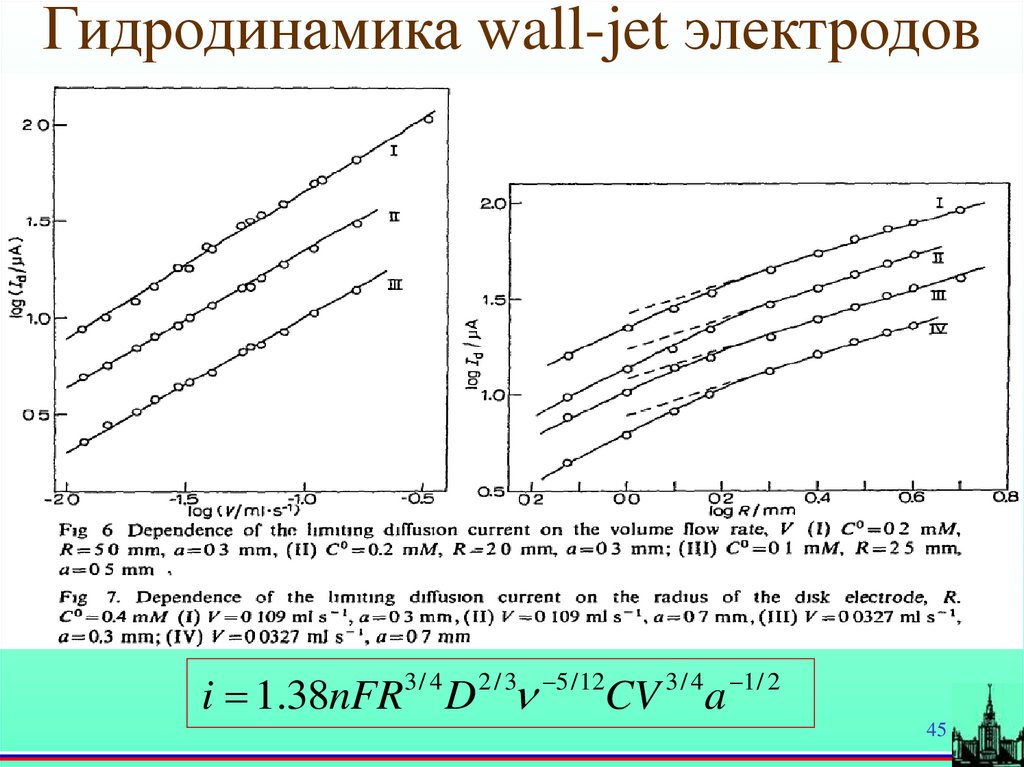
45.

Гидродинамика wall-jet электродов
i 1.38nFR3 / 4 D 2 / 3 5 / 12CV 3 / 4a 1 / 2
45

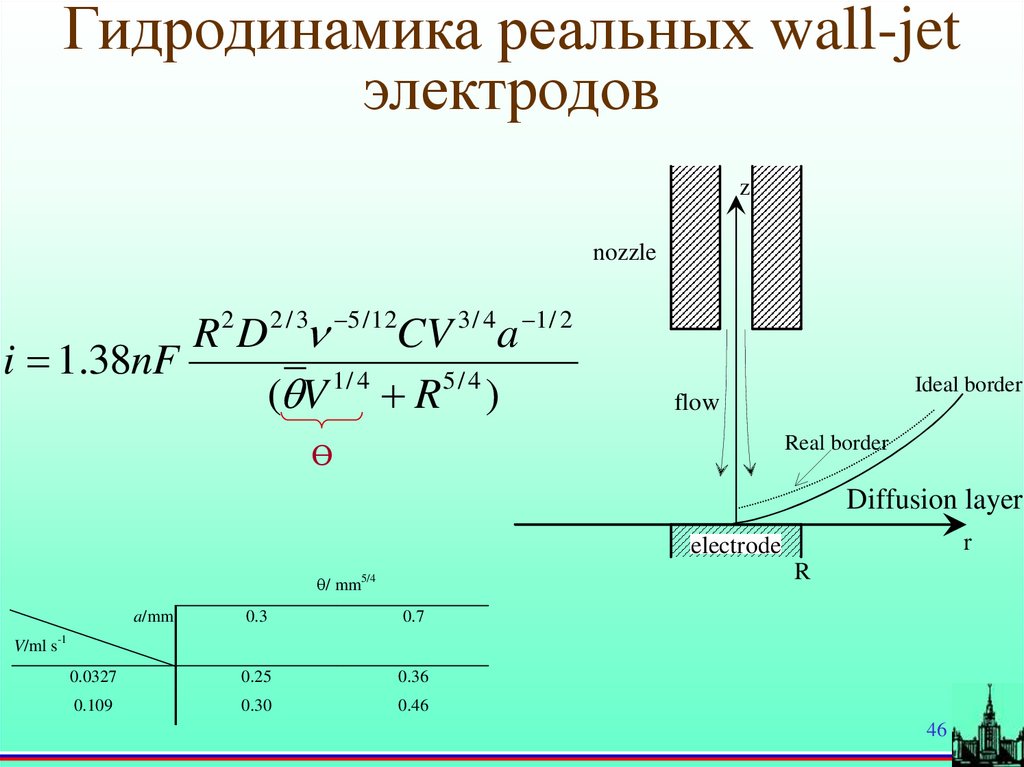
46.

Гидродинамика реальных wall-jet
электродов
z
nozzle
RD
CV a
i 1.38nF
( V 1 / 4 R5 / 4 )
2 / 3 5 / 12
2
3/ 4
1 / 2
Ideal border
flow
Real border
Ө
Diffusion layer
r
electrode
R
/ mm5/4
a/mm
V/ml s
0.3
0.7
0.0327
0.25
0.36
0.109
0.30
0.46
-1
46

47.

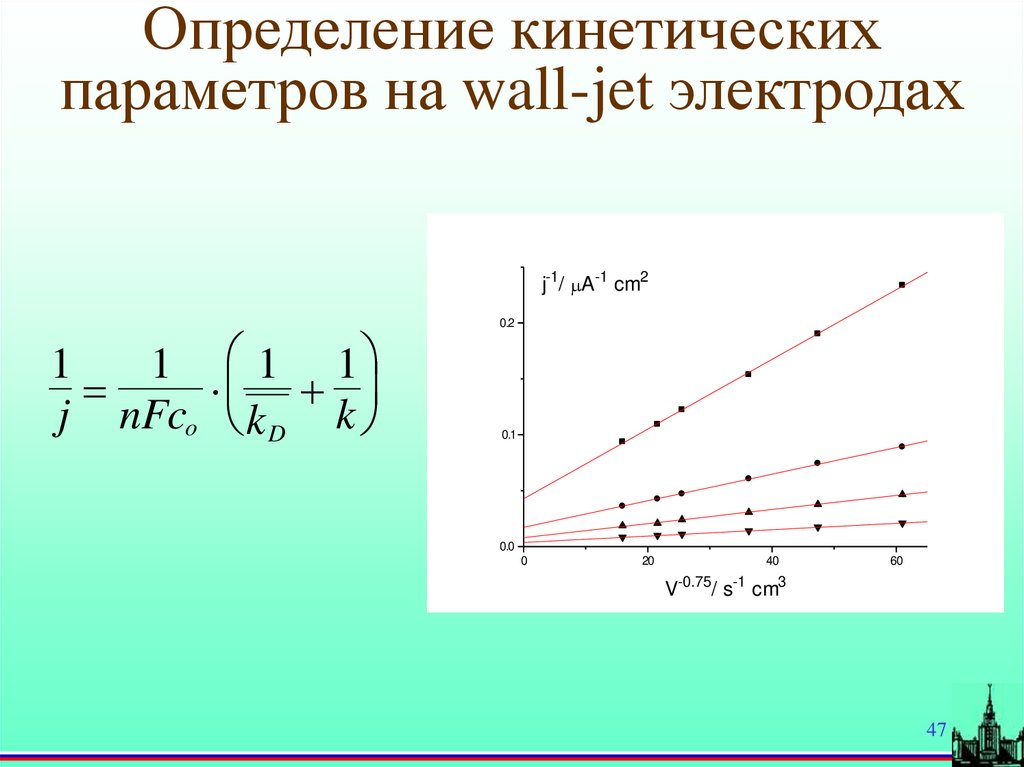
Определение кинетических
параметров на wall-jet электродах
j-1/ A-1 cm2
1
1
j nFco
1 1
kD k
0.2
0.1
0.0
0
20
40
60
V-0.75/ s-1 cm3
47

48.

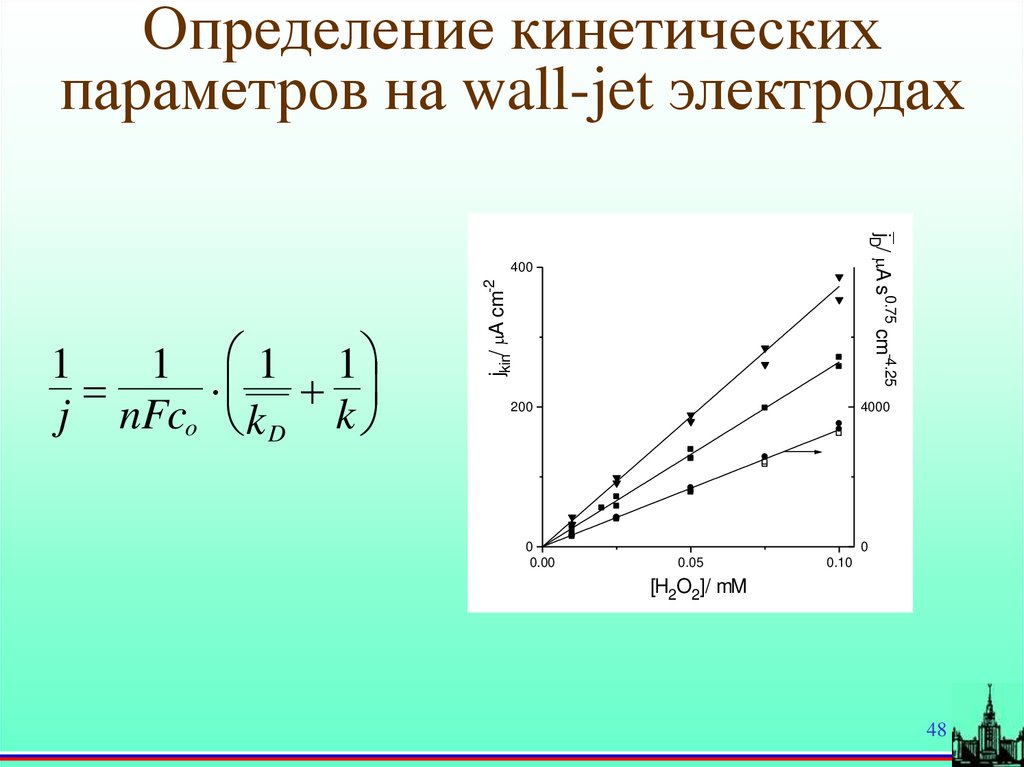
Определение кинетических
параметров на wall-jet электродах
_
jD/ A s0.75 cm-4.25
1
1
j nFco
1 1
kD k
jkin/ A cm-2
400
200
0
0.00
4000
0
0.05
0.10
[H2O2]/ mM
48

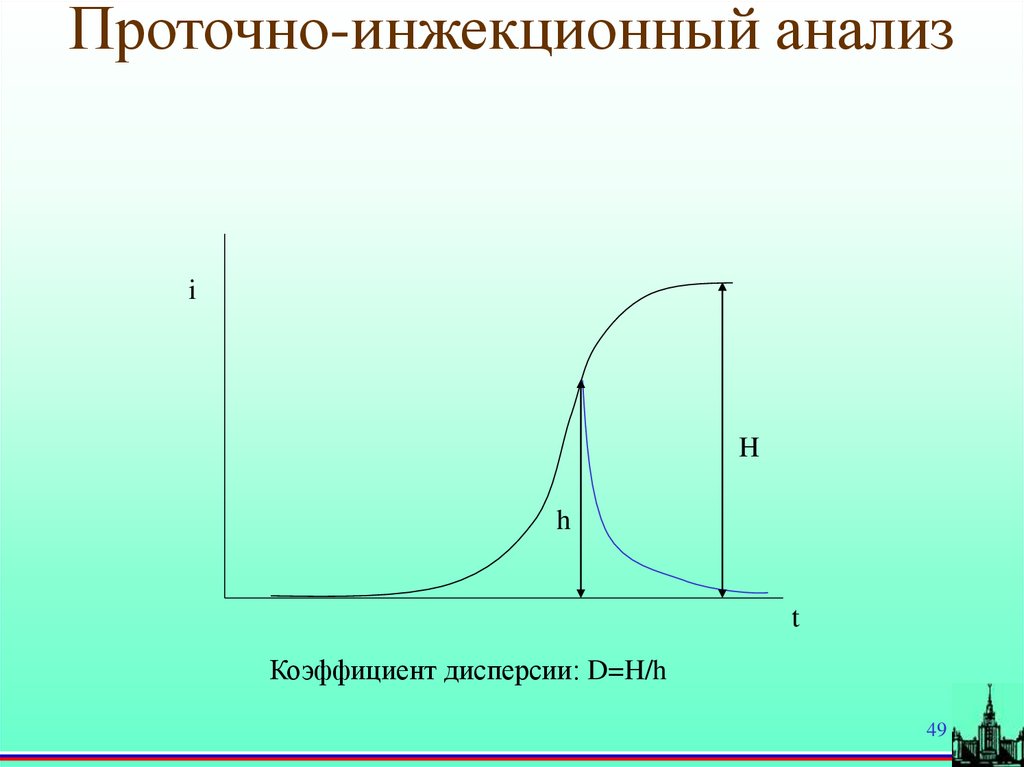
49.

Проточно-инжекционный анализ
i
H
h
t
Коэффициент дисперсии: D=H/h
49

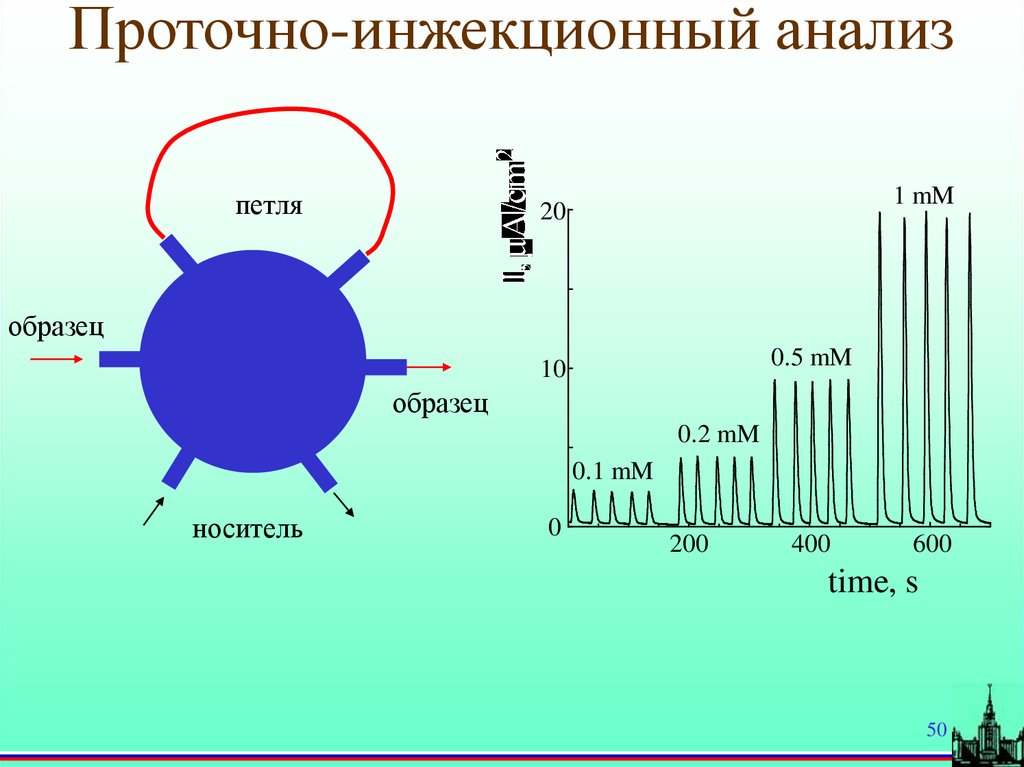
50.

Проточно-инжекционный анализ
петля
1 mM
20
образец
0.5 mM
10
образец
0.2 mM
0.1 mM
носитель
0
200
400
600
time, s
50