Похожие презентации:
Методы, основанные на электрохимическом импедансе
1. Методы, основанные на электрохимическом импедансе
2.
• импедансная спектроскопия;• ас вольтамперометрия;
• вольтамперометрия высших гармоник.
2
3.
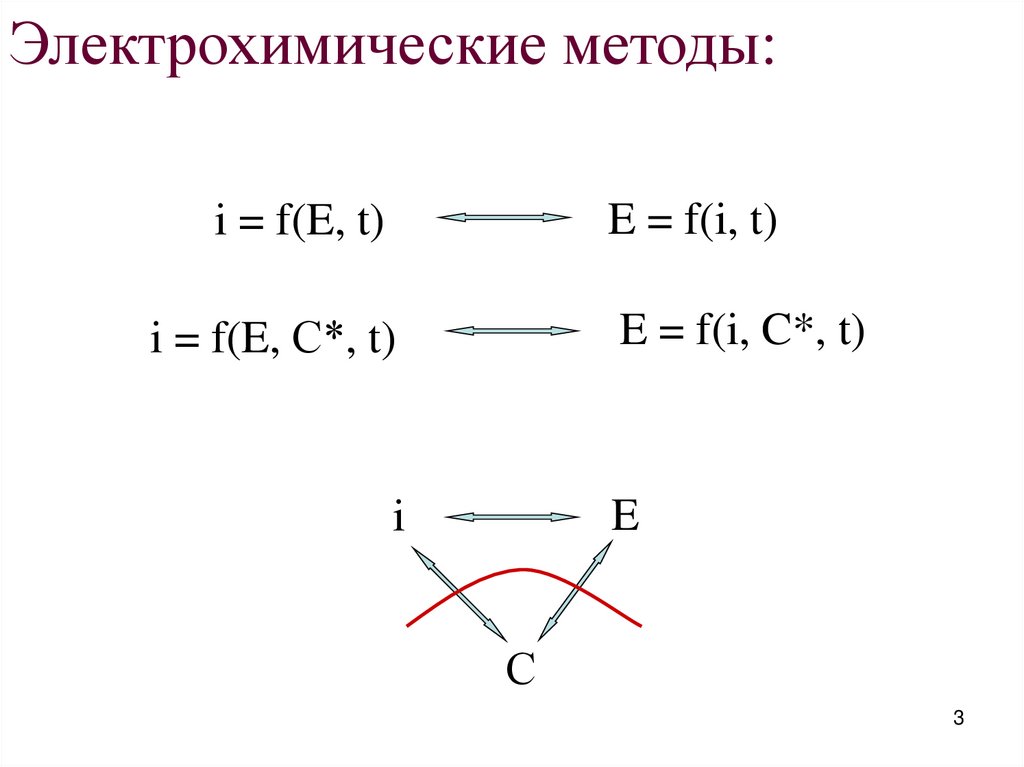
Электрохимические методы:E = f(i, t)
i = f(E, t)
i = f(E, С*, t)
E = f(i, C*, t)
E
i
С
3
4.
Диффузионные законы Фика:C ( x, t )
J ( x, t ) D
x
C ( x, t )
C ( x, t )
D
2
t
x
2
4
5.
Фазовая диаграммаe E Sin ( t )
5
6.
Импедансная спектроскопияЗадается:
e E Sin ( t )
Изучается:
i I Sin ( t )
6
7.
Фазовая диаграммаi I Sin ( t )
e E Sin ( t )
φ<0
7
8.
Фазовая диаграмма:сопротивление
e E Sin ( t )
i I Sin ( t )
8
9.
Фазовая диаграмма:емкость
de
e E Sin ( t ) i C
C E Cos( t )
dt
i C E Sin t
2
E
I
9
10.
Формулы Эйлераexp( jy) Cos( y ) jSin( y )
j 1 exp j
2
e e
Sin( y )
2j
jy
jy
e e
Cos( y )
2
jy
jy
10
11.
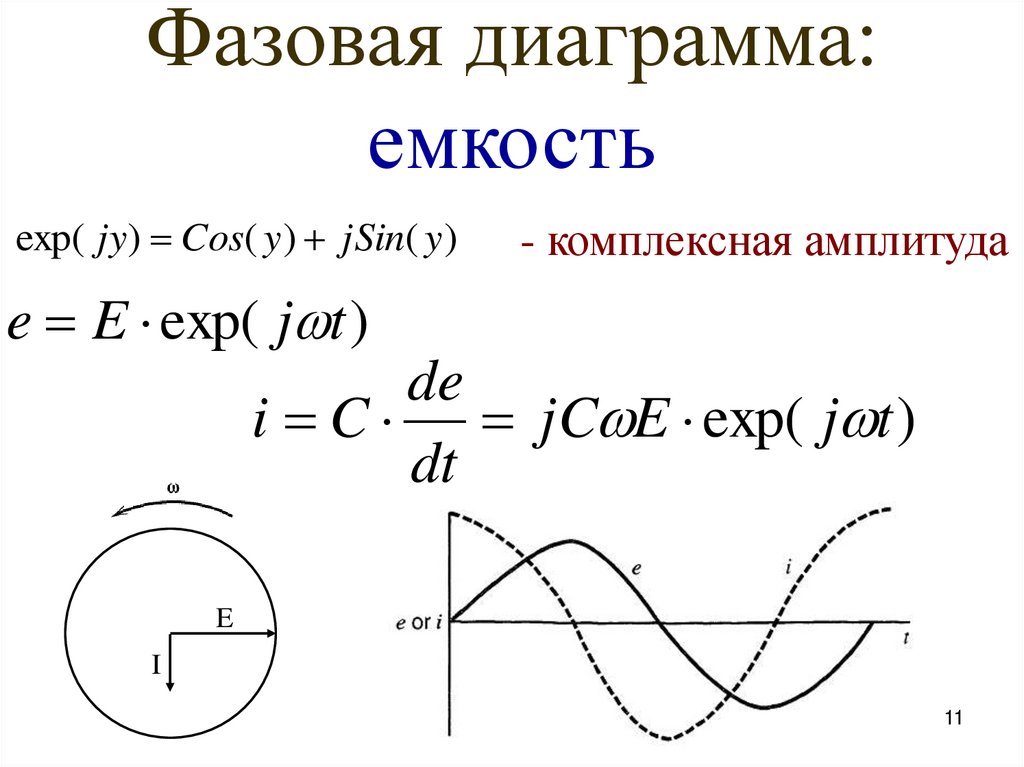
Фазовая диаграмма:емкость
exp( jy) Cos( y ) jSin( y )
- комплексная амплитуда
e E exp( j t )
de
i C jC E exp( j t )
dt
E
I
11
12.
ИмпедансZ ( ) | Z | exp( j )
Z ( ) Re Z j Im Z
| Z | (Re Z ) (Im Z )
2
2
2
Re( Z ) | Z | Cos( )
Im( Z ) | Z | Sin ( )
12
13.
ИмпедансZ ( ) Re Z j Im Z
Re( Z ) | Z | Cos( )
Im( Z ) | Z | Sin ( )
13
14.
АдмиттансZ ( ) Re Z j Im Z
1
Re Z j Im Z
Y ( )
2
2
Z ( ) (Re Z ) (Im Z )
14
15.
Уравнение ток - перенапряжение5
i/i0
E Eeq
nF
(1 ) nF
[ R]0 RT
[O]0
i i0
e
e RT
[O]*
[ R]*
0
-100
0
100
mV
-5
15
16.
Предельные случаиа) отсутствие влияния массопереноса
nF
(1 ) nF
RT
RT
i i0 e
e
Butler-Volmer
а1) малые перенапряжения
nF
i i0
RT
RT/F ≈ 25 mV
а2) большие перенапряжения
i i0 e
nF
RT
16
17.
Импеданс стадии разрядаe E exp( j t )
i I exp{ j ( t )}
RT
Z Rct
nFi0
0
17
18.
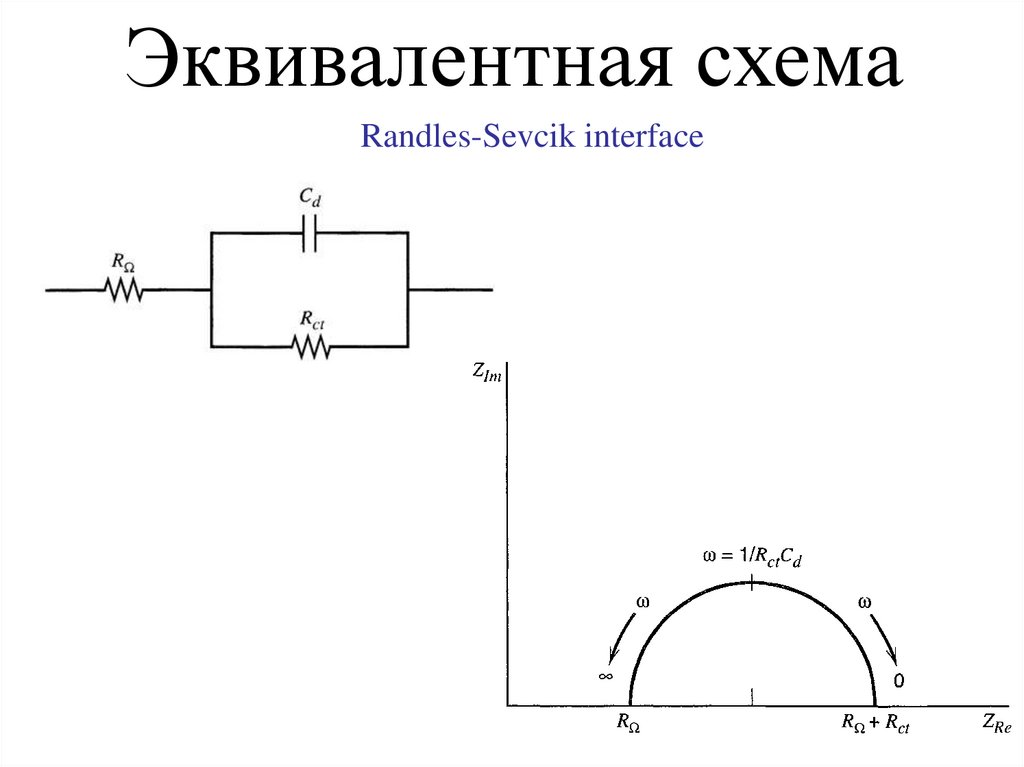
Эквивалентная схемаRandles-Sevcik interface
18
19.
Реальный анализRandles-Sevcik interface
Элемент постоянной фазы:
Y ( ) A( j )
0 1
19
20.
Эквивалентная схемаZ''
-16
-6
Rb
0
Cdl
10
Z'
Y''
0.50
0.25
0
0
0.25
0.50
0.75
1.00
Y'
20
21.
Диффузионный импедансe E exp{ j t}
i I exp{ j ( t )}
C ( x, t )
C ( x, t )
D
t
x 2
2
C ( x, t ) C ( x ) C ( x ) exp( j t )
2 C ( x )
j C ( x ) D
2
x
21
22.
Диффузионный импеданс2 C ( x )
j C ( x ) D
2
x
j
j
B exp x
C ( x ) A exp x
D
D
22
23.
Warburg impedanceполубесконечное приближение
j
j
B exp x
C ( x ) A exp x
D
D
x
C 0
A 0
i
C ( x )
J ( x 0) D
x x 0 nF
C (0)
1
i
nF j D
23
24.
Warburg impedanceC (0)
1
i
nF j D
dE dE dC dE
1
Z
di dC di dC nF j D
1
dE
1 j
Z
dC nF D
24
25.
Эквивалентная схемаRb
Cdl
ZW
RW
Rct
RT
1
1
1/ 2 * 1/ 2 *
RW 2Cd 2 2
n F A 2 DO CO DR CR
25
2
26.
2627.
Ограниченная диффузияпропускные граничные условия
j
j
B exp x
C ( x ) A exp x
D
D
x l
C C*
dE 1 tanh l j / D
Z
j D
dC nF
27
28.
Профиль концентрации идиффузионный слой
28
29.
ГидродинамикаВращающийся дисковый электрод
Уравнение Левича:
ω
il 0.620nFAD
2/3
C
1 / 6
1/ 2
29
30.
ГидродинамикаВращающийся дисковый электрод
Уравнение Левича:
i 0.620nFAD2 / 3 1 / 6 1 / 2C
D
i nFA C
1.61D
1/ 3 1/ 6
1 / 2
C*
Co
x
δ
30
31.
Ферроцианид (1 мМ), вращающийсядисковый электрод 1800 rpm
Rd Z ( 0)
(○) – ¾ id, (∆) – ½ id, (●) – ¼ id. (a) – теоретическая кривая по приближению Нернста
31
32.
Ограниченная диффузияотражательные граничные условия
j
j
B exp x
C ( x ) A exp x
D
D
x l
C
0
x
dE 1 ctnh l j / D
Z
j D
dC nF
32
33.
Ограниченная диффузияотражательные граничные условия
33
34.
Conducting polymers• electronic conductivity
• ionic conductivity
Polypirrole:
R
N
-
-e
R
R
N
N
n
C. K. Chiang, C. R. Fincher, Y. W. Park, A. J. Heeger, H. Shirakawa, E. J. Louis, S. C.
Gau, and A. G. Macdiarmid, Physical Review Letters 39, 1098 (1977)
34
35.
Полимеризация пиррола.N
H
-e
+
H
+
-H
N
Инициация
+
H
H
. N+
H H
N
+
-e
+
-H
Рост цепи
H
Обрыв цепи
2 .
N
+
- 2 H+
H
H
N
N
35
36.
Проводимость полипирролаВосстановленный
полипиррол
H
H
H
N
N
N
N
N
H
H
H
Полярон
Биполярон
N
.
H
H
N
N
N
+
N
H
H
H
H
N
+
N
H
N
N
+
N
H
H
36
37.
Полианилинлейкоэмеральдин
эмеральдин
пернигранилин
H
H
N
N
H
H
N
+
.
N
N
N
37
38.
Окно проводимостиполианилин
38
39.
Проводящие полимерыRb
C
Zd
Rct
39
40.
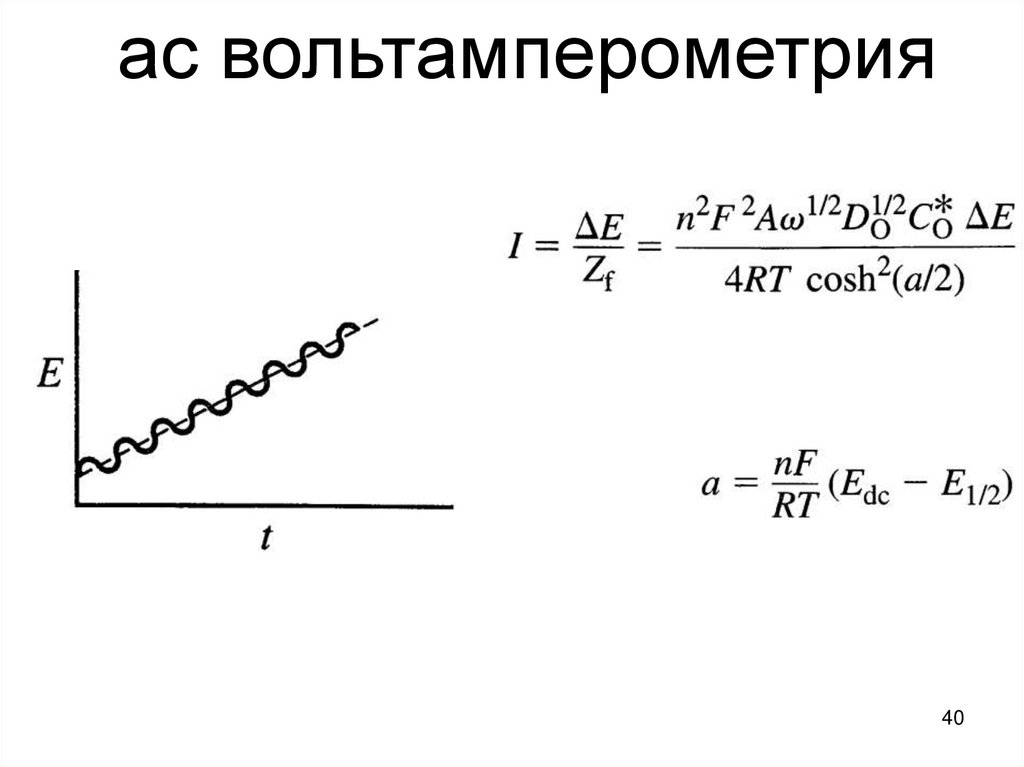
ас вольтамперометрия40
41.
ас вольтамперометрия41
42.
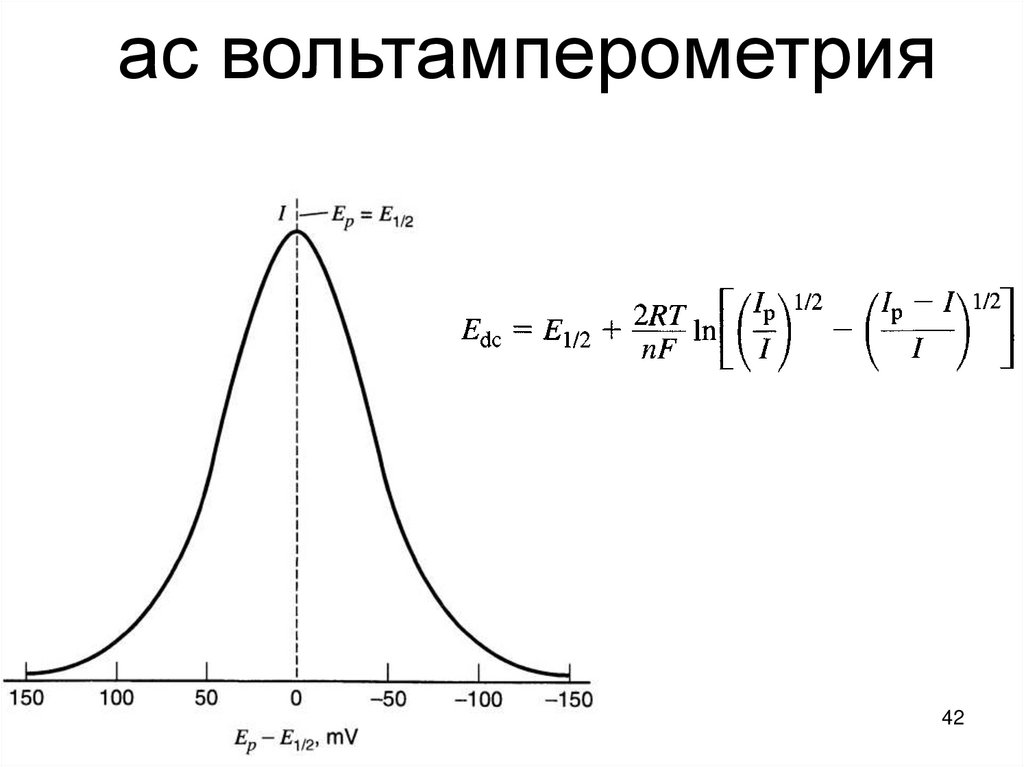
ас вольтамперометрия42
43.
Циклическая ас вольтамперометрияОбратимые системы
43
44.
Циклическая ас вольтамперометрияКвазиобратимые системы
44
45.
CacV 1 мМ ацетилацетоната Fe(III) в ацетоне, ∆E = 5 mV,v = 100 Mv/s, ω/2π = 400 Hz
45

















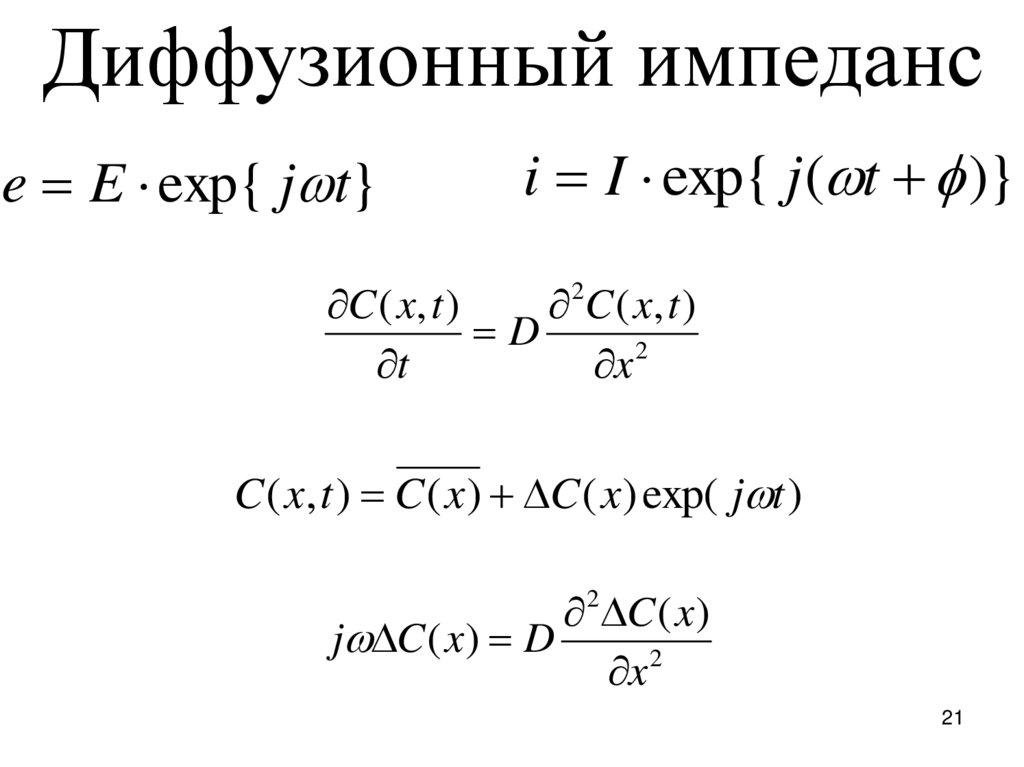























 Физика
Физика Химия
Химия








