Похожие презентации:
Итоговый урок повторения по алгебре. 7 класс
1.
Учитель Сухачева Е.В.2.
ДробиУравнения
Степени
Функции
Формулы
Системы уравнений
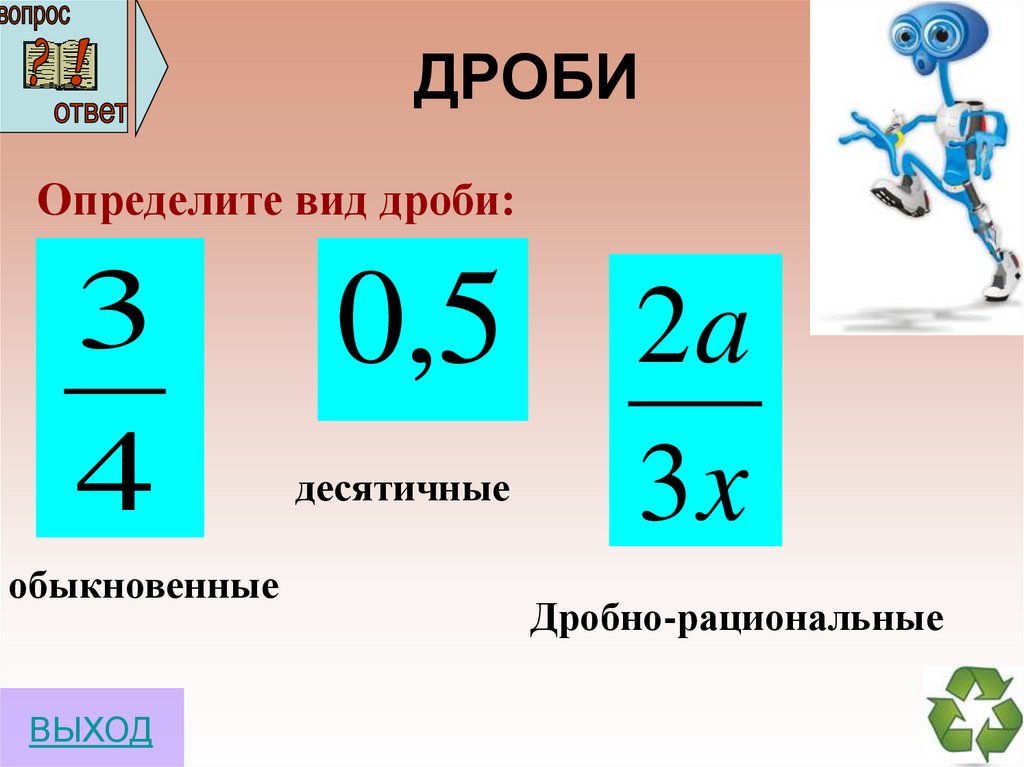
3. ДРОБИ
Определите вид дроби:3
4
обыкновенные
ВЫХОД
0,5 2a
десятичные
3x
Дробно-рациональные
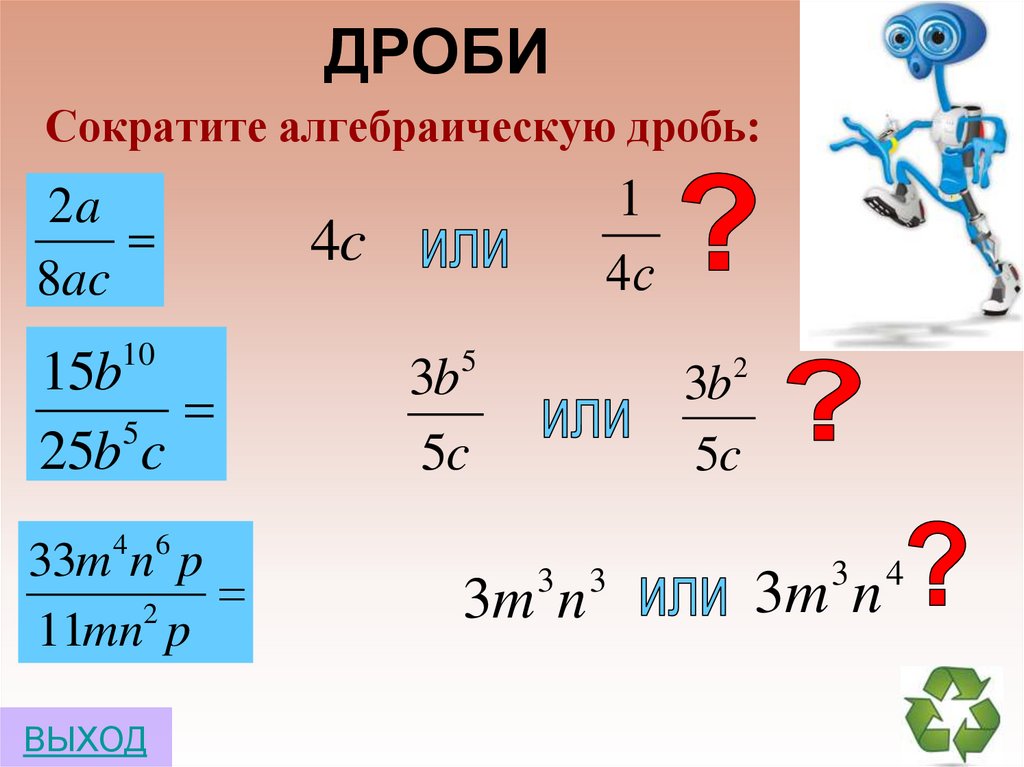
4. ДРОБИ
Сократите алгебраическую дробь:2a
8ac
10
15b
5
25b c
1
4с
4c
5
2
3b
5c
3b
5c
4 6
33m n p
2
11mn p
ВЫХОД
3
3m n
3
3
3m n
4
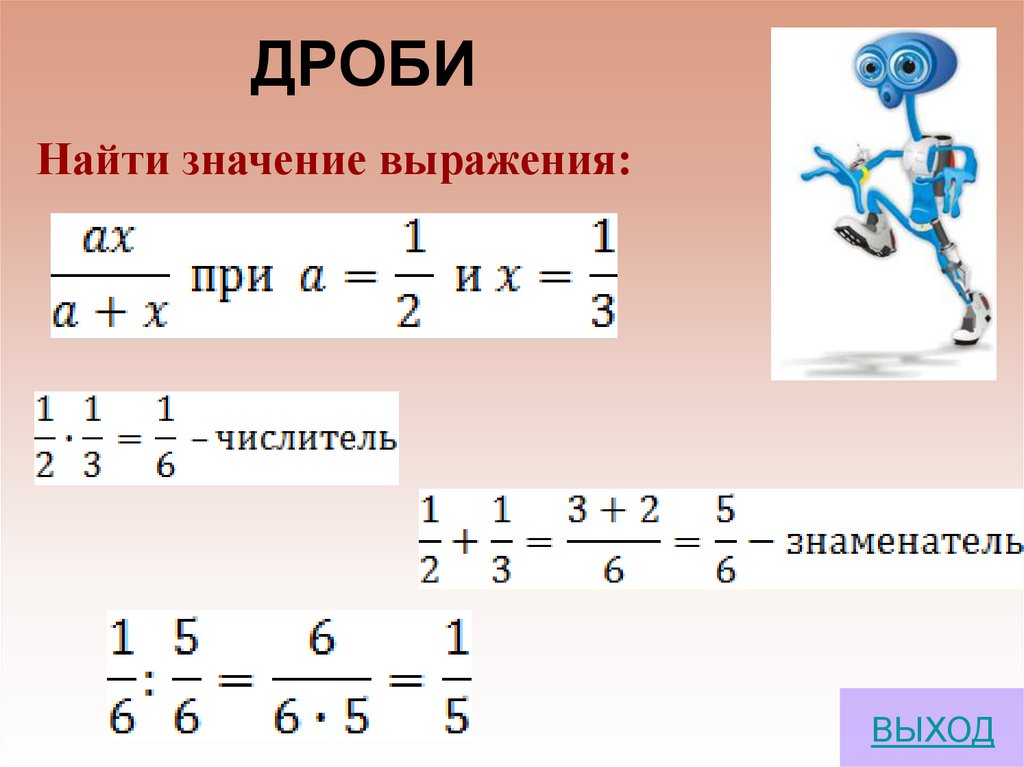
5. ДРОБИ
Найти значение выражения:ВЫХОД
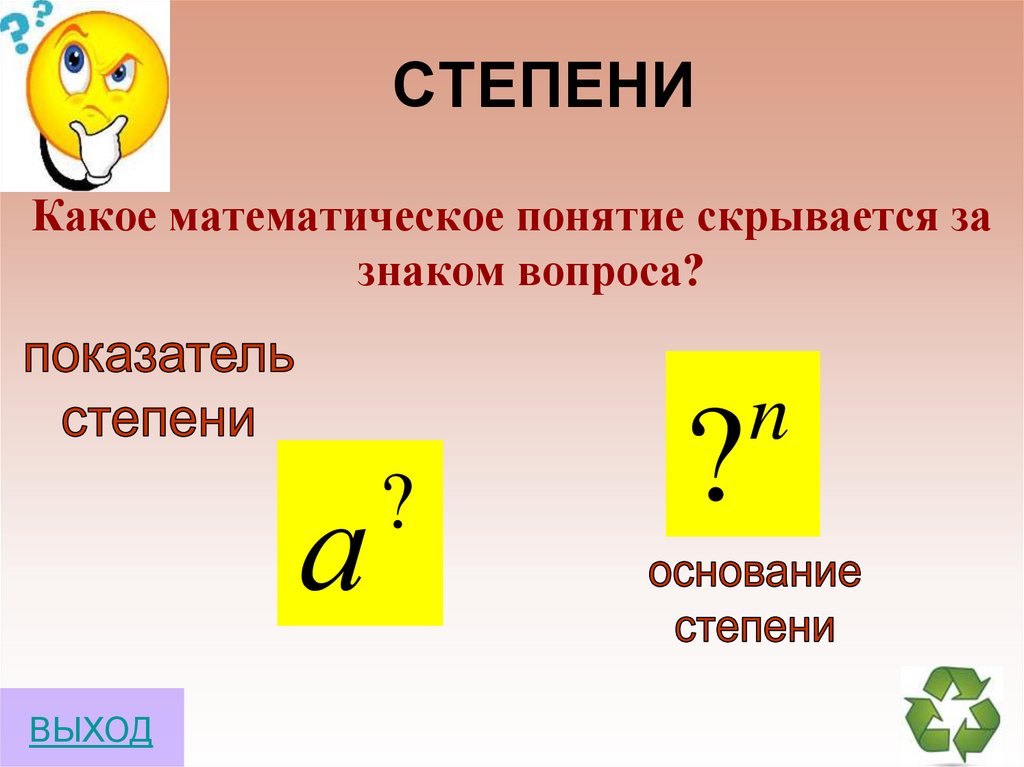
6. СТЕПЕНИ
Какое математическое понятие скрывается зазнаком вопроса?
а
ВЫХОД
?
?
n
7. СТЕПЕНИ
Свойства степеней1
• a =a
0
• a =1
m
n
m+n
• a a =a
m
n
m-n
• a :a =a
m
n
mn
• (a ) =a
ВЫХОД
• (a
n
n
n
b) =a b
8. СТЕПЕНИ
Найдите значение выражения:(с ) с
2 4
0
с (с )
5
с
с
8
4 6
а (а с)
6
а с
3
ВЫХОД
2
с
20
2
ас
9. СТЕПЕНИ
Вычислите:x (y )
2
3 5
2 (x y )
14
5 3
4
x
2
ВЫХОД
3 4
(2ac )
3 5
10
6(a ) c
2
8c
11
3a
10.
1) Найдите значение выражения(18a 27a ) : (9a ) 10a : (5a)
4
2
3
3
3а
2) Найдите разность многочленов
3х 1
и
3х 3х 1
2
3) Упростите выражение
3х(х-2)-5х(х+3)
6 x 3x
2
2 x 21x
2
ВЫХОД
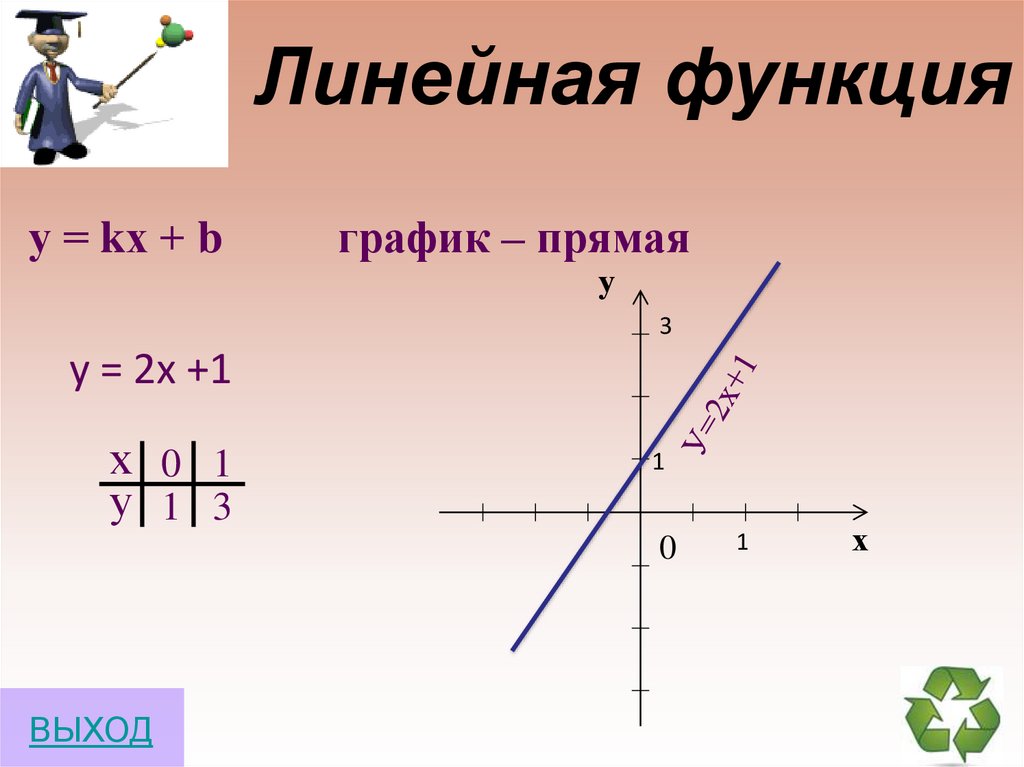
11.
Линейная функцияу = kх + b
график – прямая
у
3
у = 2х +1
х 0 1
у 1 3
1
0
ВЫХОД
1
х
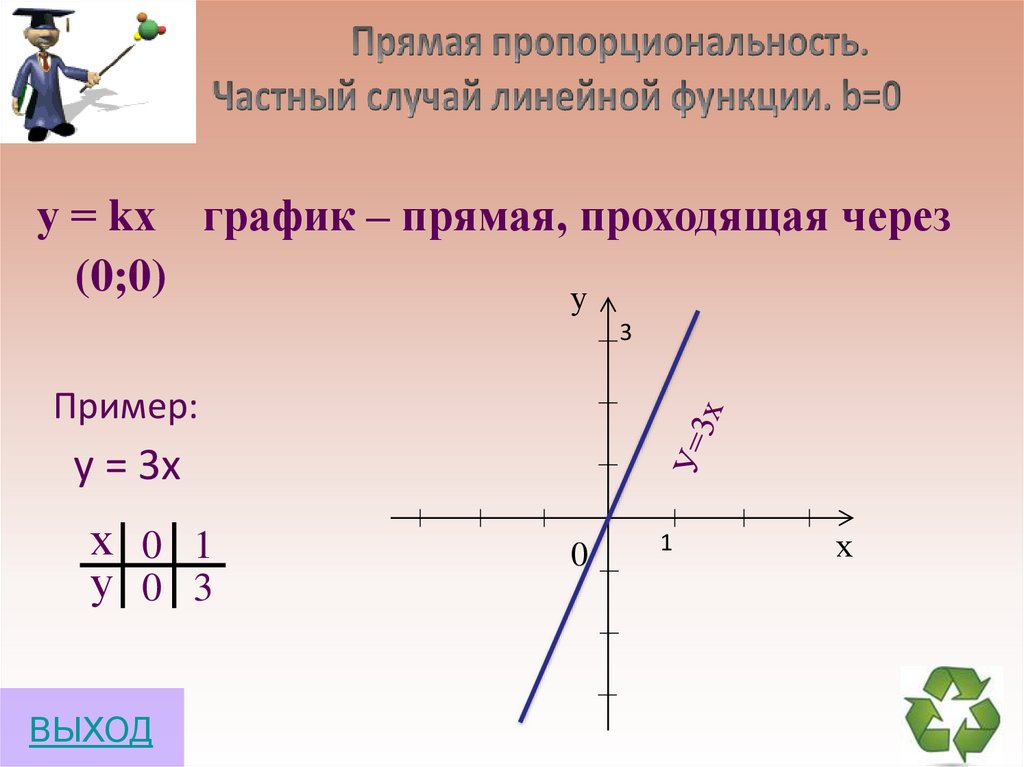
12.
у = kх график – прямая, проходящая через(0;0)
у
3
Пример:
у = 3х
х 0 1
у 0 3
ВЫХОД
0
1
х
13.
уy= 2
2
прямая,
параллельная
оси ОХ
0
х
1
y= -3
-3
ВЫХОД
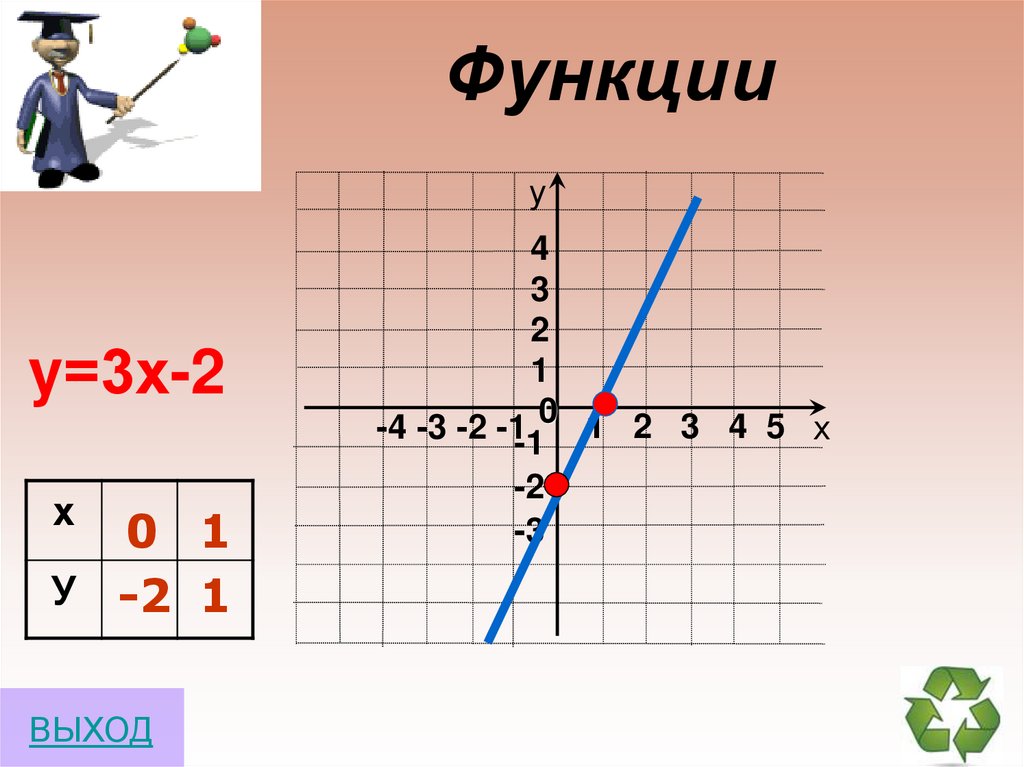
14. Функции
уy=3х-2
х
0 1
У -2 1
ВЫХОД
4
3
2
1
-4 -3 -2 -1-10 1 2 3 4 5 х
-2
-3
15.
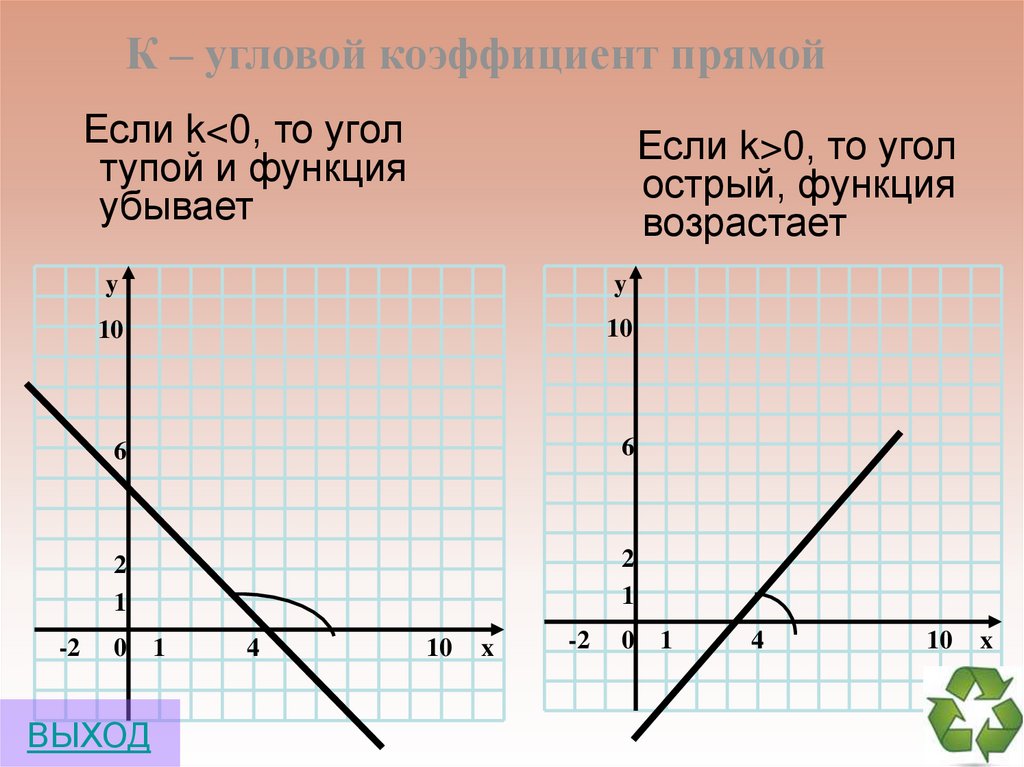
К – угловой коэффициент прямойЕсли k<0, то угол
тупой и функция
убывает
-2
Если k>0, то угол
острый, функция
возрастает
y
y
10
10
6
6
2
1
2
1
0
ВЫХОД
1
4
10
x
-2
0 1
4
10
x
16.
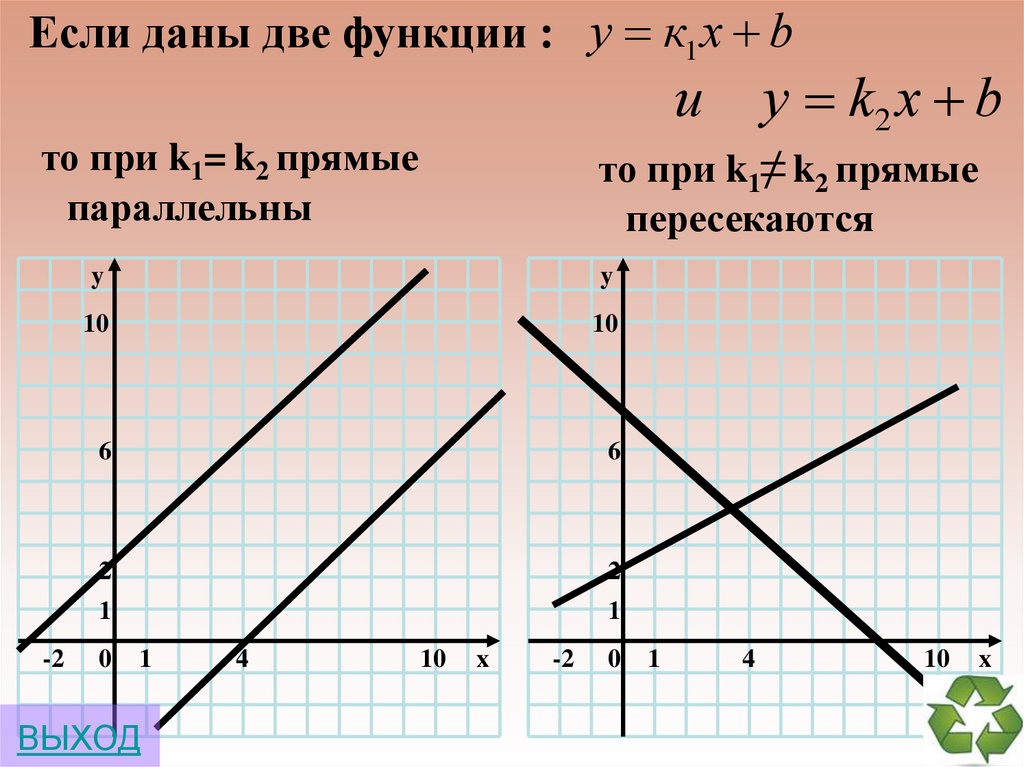
Если даны две функции : у к1 x by k2 x b
и
то при k1= k2 прямые
параллельны
-2
то при k1≠ k2 прямые
пересекаются
y
y
10
10
6
6
2
2
1
1
0
1
ВЫХОД
4
10
x
-2
0
1
4
10
x
17. Функции
у4
3
2
1
-4 -3 -2 -1-1
1 2 3 4 5 х
-2
-3
Угловые коэффициенты равныВЫХОД
графики линейных функций
параллельны.
18. Функции
у4
3
2
1
-4 -3 -2 -1-1
1 2 3 4 5 х7
-2
-3
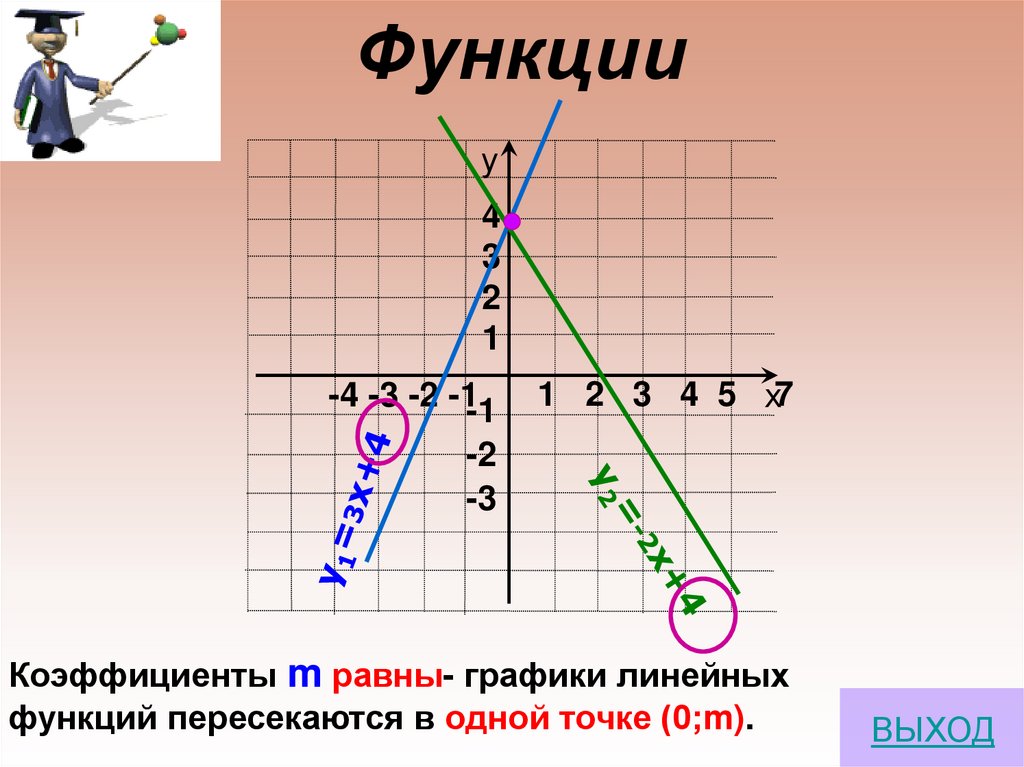
Коэффициенты m равны- графики линейных
функций пересекаются в одной точке (0;m).
ВЫХОД
19.
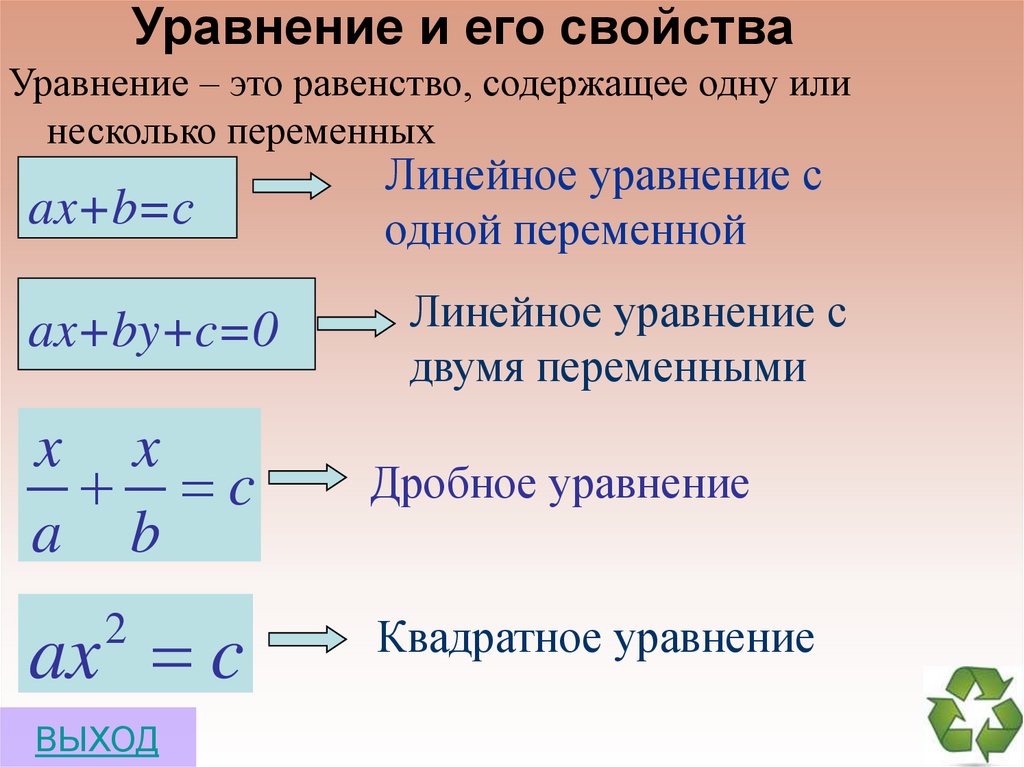
Уравнение и его свойстваУравнение – это равенство, содержащее одну или
несколько переменных
ax+b=с
ax+by+c=0
Линейное уравнение с
одной переменной
Линейное уравнение с
двумя переменными
x x
c
a b
Дробное уравнение
ax c
Квадратное уравнение
2
ВЫХОД
20.
УравненияРешить уравнение:
1) 2 - 3(х+2) = 5 - 2х
-3х+2х = 5+4
-х = 9
Х= -9
2) X = - X
X+X=0
2X=0
X=0
ВЫХОД
x x 3
3)
4 8 2
x x 3
8
4 8 2
2x+x=12
3x=12
x=4
21.
УравненияРешите уравнения:
1) (х-2)(х+3)=0
2) x 4
X-2=0 или Х+3=0
Х=2
Х= - 3
Ответ:-3; 2.
Х= - 4 и Х= 4
Ответ: -4; 4.
3) x 16
2
ВЫХОД
Х= -4 и Х= 4
Ответ: -4; 4.
22.
УравненияНайдите корень уравнения:
x 4 x
1)
5
3
2
2(х-4)+3х=30
5х=38
Х=7,6
2) 5 x 3 2
5х-3=2 и 5х-3=-2
5х=5
5х=1
Х=1
Х=0,2
Ответ: 0,2; 1.
ВЫХОД
23.
Формулы сокращенногоумножения
(a b) a 2ab b
2
(a b) a 2ab b
2
2
2
2
2
(a b)(a b) a b
2
2
(a b)(a ab b ) a b
3
(a b)(a ab b ) a b
3
2
2
ВЫХОД
2
2
3
3
24. Разложите на множители:
a 10ab 25b2
1 6
4m c
9
2
2
(a 5b)
2
1 3
1 3
(2m c )(2m c )
3
3
2
2
24a c 3a c 3a c(8a 1)
3
ВЫХОД
25.
Разложите на множители:1)3a 12
2
3(a 4) 3(a 2)(a 2)
2
2)5a 20a b 20b
4
2
2
5(a 4a b 4b ) 5(a 2b)
4
2
2
2
3) y 27
9
ВЫХОД
( y 3)( y 3 y 9)
3
6
3
2
26.
Решите уравнения:2
x ( x 1) 0
1) x x 0
3
x ( x 1)( x 1) 0
x 1, x 0, x 1.
2
2
x (25 x 1) 0
2
x (5 x 1)(5 x 1) 0
1
1
x 0, x , x .
5
5
x ( x 1) 4( x 1) 0
2
( x 4)( x 1) 0
2
3) x 4 x x 4 0 ( x 2)( x 2)( x 1) 0
3
2
2, 1, 2.
ВЫХОД
27.
Система уравнений и её решенияОпределения
• Системой уравнений называется некоторое количество
уравнений, объединенных фигурной скобкой. Фигурная
скобка означает, что все уравнения должны выполняться
одновременно
• Решением системы уравнений с двумя переменными
называется пара значений переменных, обращающая
каждое уравнение системы в верное равенство
• Решить систему уравнений - это значит найти все её
решения или установить, что их нет
28.
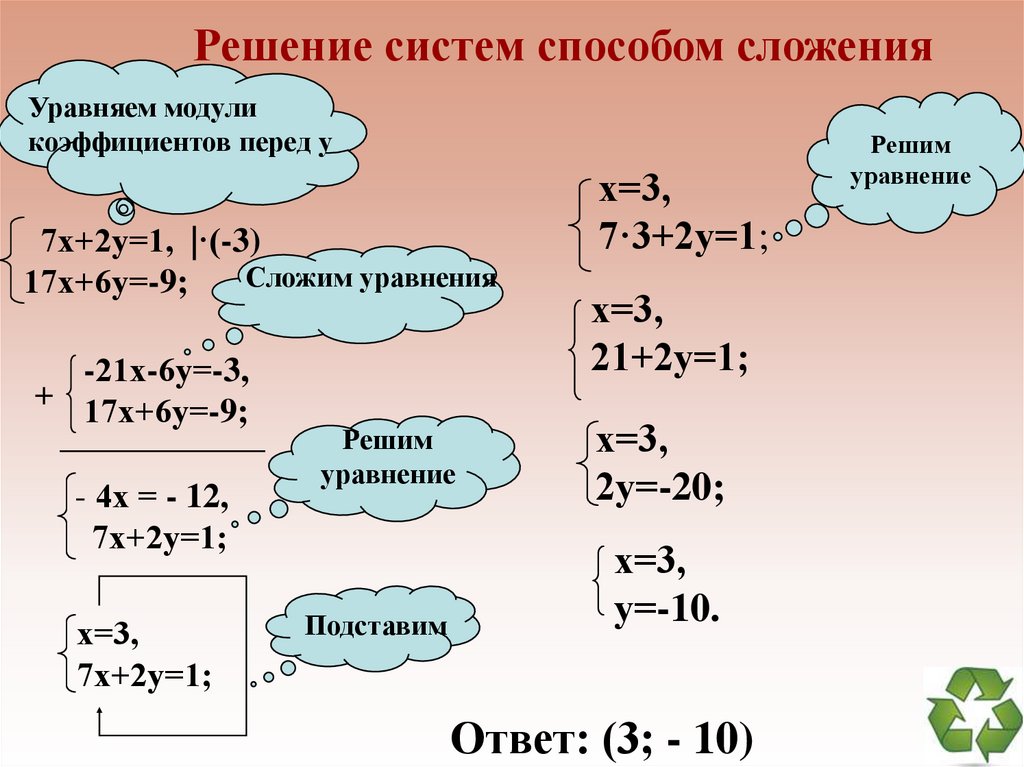
Способы решения систем уравнений29.
Решение системы способом подстановкиВыразим у через х
у=2х+4,
7х - у=1;
у - 2х=4,
7х - у =1;
Подставим
у=2х+4,
х=1;
у=2х+4,
7х - (2х+4)=1;
Решим второе
уравнение
у=6,
х=1.
5х = 5;
х=1;
Подставим
ВЫХОД
7х - 2х - 4 = 1;
Ответ: х=1; у=6.
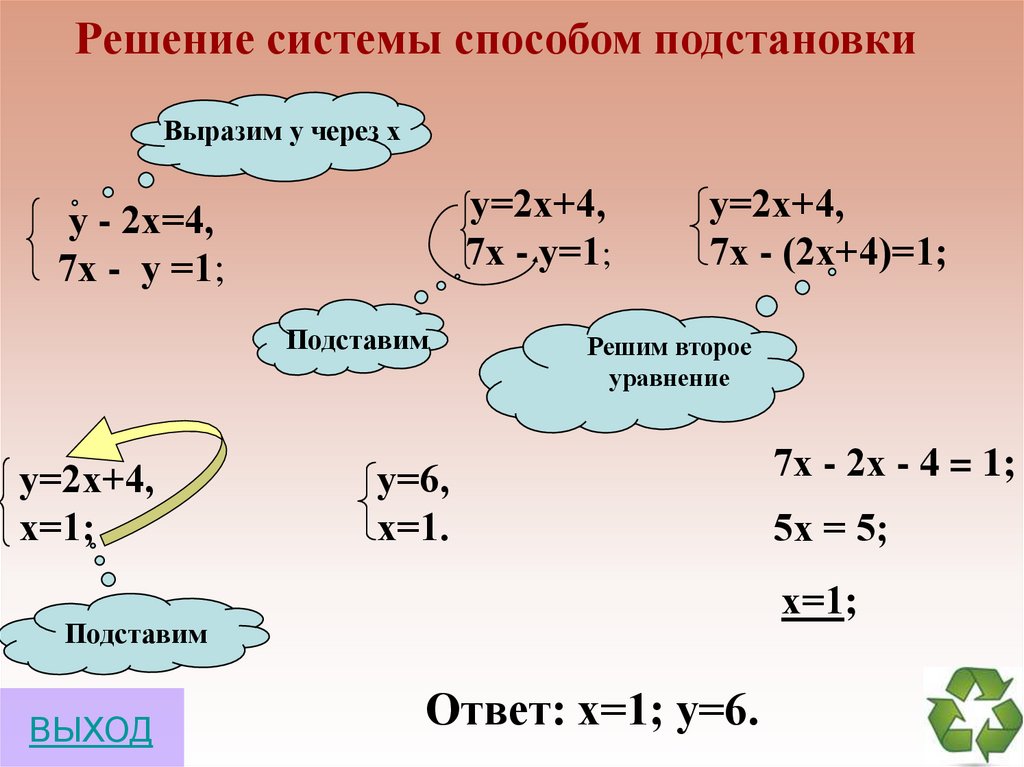
30.
Решение систем способом сложенияУравняем модули
коэффициентов перед у
7х+2у=1, |·(-3)
Сложим уравнения
17х+6у=-9;
-21х-6у=-3,
+
17х+6у=-9;
____________
- 4х = - 12,
7х+2у=1;
х=3,
7х+2у=1;
Решим
уравнение
Подставим
х=3,
7·3+2у=1;
х=3,
21+2у=1;
х=3,
2у=-20;
х=3,
у=-10.
Ответ: (3; - 10)
Решим
уравнение
31.
Решение системы графическим способому - х=2,
у+х=10;
Выразим у
через х
y
у=х+2,
у=10-х;
Построим график
первого уравнения
6
у=х+2
х 0 -2
у 2 0
Построим график
второго уравнения
y=x+2
10
y=10 - x
2
1
-2
0
1
4
у=10 - х
х 0 10
у 10 0
Ответ: (4; 6)
10
x
32.
Способ введения новой переменной1. Bведем обозначения :
1
x
1
x
2
1
1
11,
a, b.
x
y
y
2. Подставим в систему уравнений
2
1.
1 1
y
a и b вместо и , получим систему
x y
3. Решим эту систему
a 2b 11,
относительно a и b:
a 2b 1.
2a=10
1
1
a=5, тогда 2в=6
4. Теперь найдем х и y,
5,
x
.
в=3.
x
5
используя наши
обозначения
1
1
1
1
3, y .
Ответ: x , y .
y
3
5
3
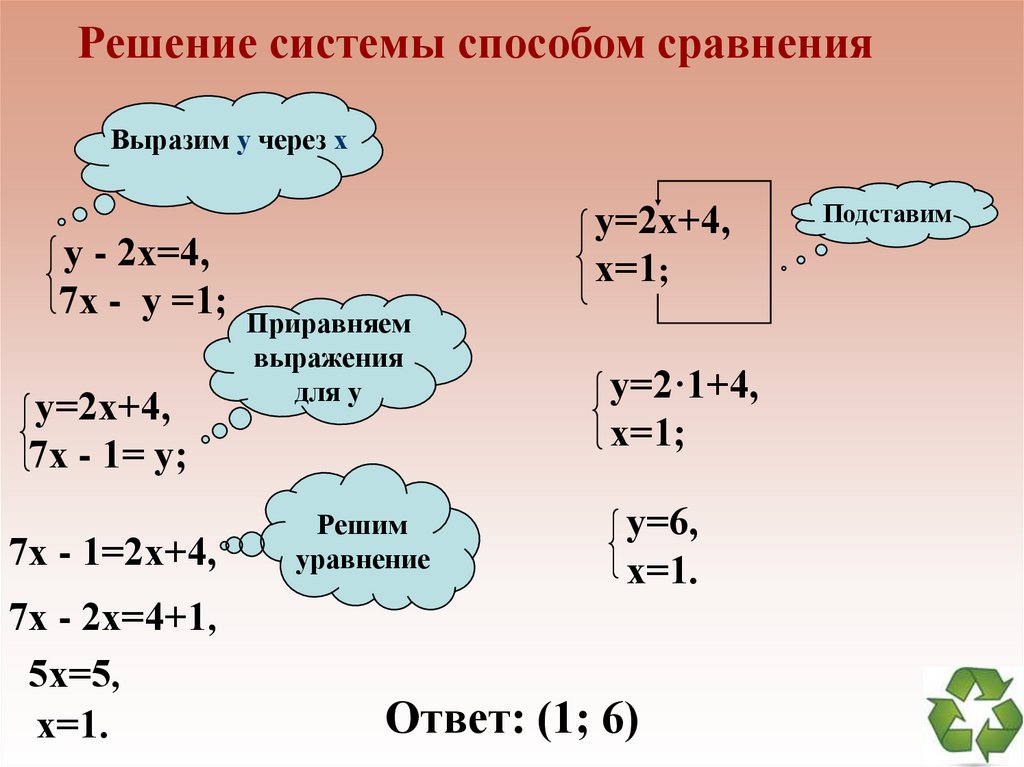
33.
Решение системы способом сравненияВыразим у через х
у - 2х=4,
7х - у =1;
у=2х+4,
7х - 1= у;
7х - 1=2х+4,
7х - 2х=4+1,
5х=5,
х=1.
у=2х+4,
х=1;
Приравняем
выражения
для у
Решим
уравнение
у=2·1+4,
х=1;
у=6,
х=1.
Ответ: (1; 6)
Подставим
34.
Решение системы методом определителейСоставим матрицу из коэффициентов
при неизвестных
7х+2у=1,
17х+6у=-9;
=
7
17
2
= 7·6 - 2·17 = 42 - 34 = 8
6
1
x =
-9
7
y=
17
х=
Составим определитель x, заменив в определителе первый столбец
на столбец свободных
членов
x
2
= 1·6 - 2·(-9) = 6 + 18 = 24
6
Составим определи1 = 7·(-9) - 1·17 = - 63 -17= -80 тель y, заменив в определителе второй столбец
-9
на столбец свободных
Найдем
членов
=
24
8
хиу
= 3;
у=
y
=
-80
= -10.
8
Ответ: х=3; у= -10.
ВЫХОД



















 Математика
Математика








