Похожие презентации:
Электромагнетизм
1.
•Электромагнетизм.
Закон Био-Савара-Лапласа. Закон Ампера.
Сила Лоренца.
2.
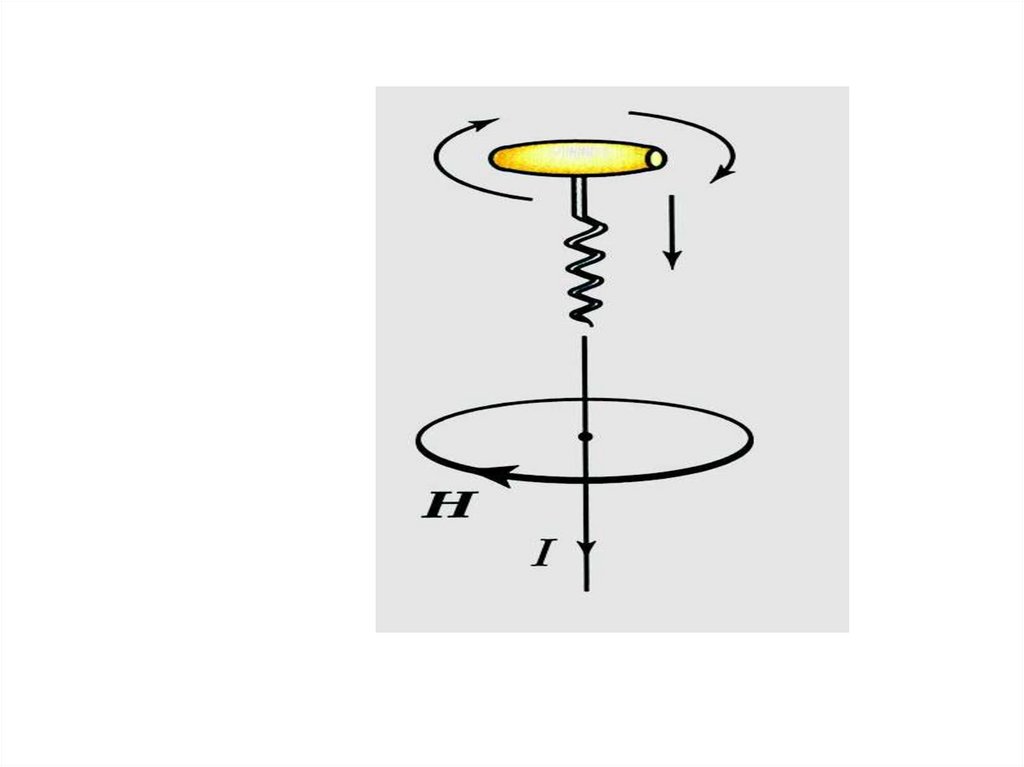
3.
4.
0 I
dB
[
d
l
r
]
3
4 r
( о =4 ·10-7 Гн/м)
Таблица . Магнитная проницаемость ферромагнетиков
• Железо 5000-10000
Пермаллой1 30 000-50 000
Кобальт 80-100
Чугун 600-800
Никель 40-50
5.
0 IdB
[
d
l
r
]
3
4 r
0 I
dB
dl
sin
2
4 r
a
r
sin
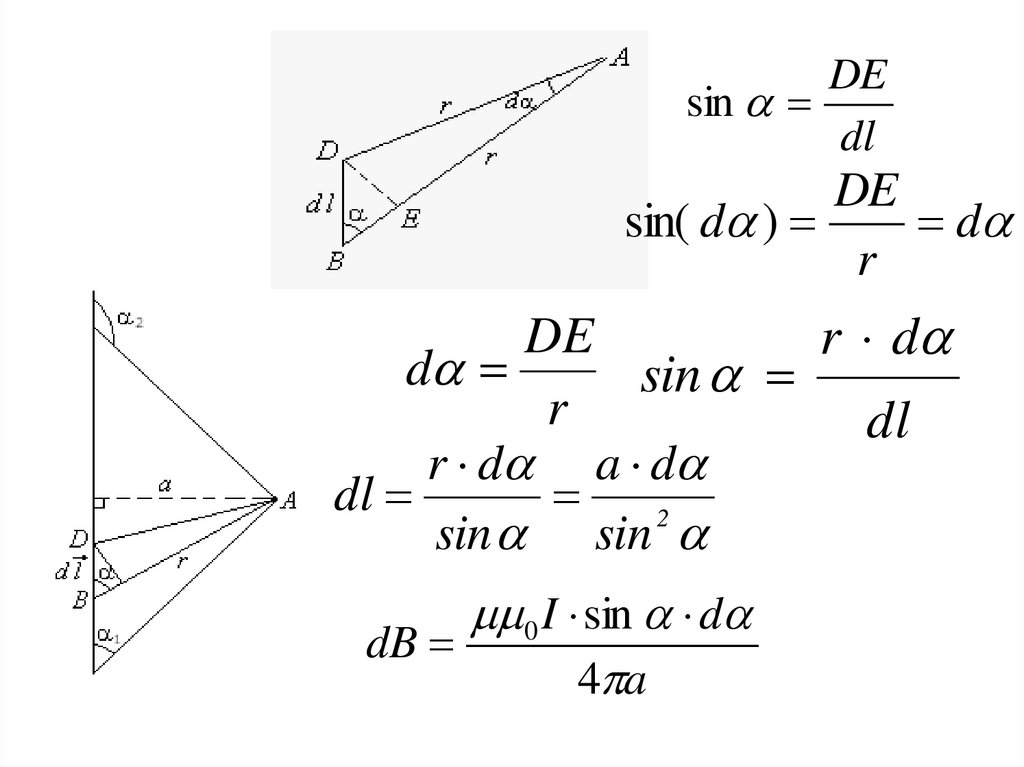
6.
DEsin
dl
DE
sin( d )
d
r
DE
r d
d
sin
r
dl
r d a d
dl
2
sin sin
0 I sin d
dB
4 a
7.
0 I sin d
dB
4 a
0 I
0 I
cos 1 cos 2
B
sin d
4 a 1
4 a
2
Для бесконечно длинного проводника с
током. 1 = 0, 2 =
0 I
B
2 a
8.
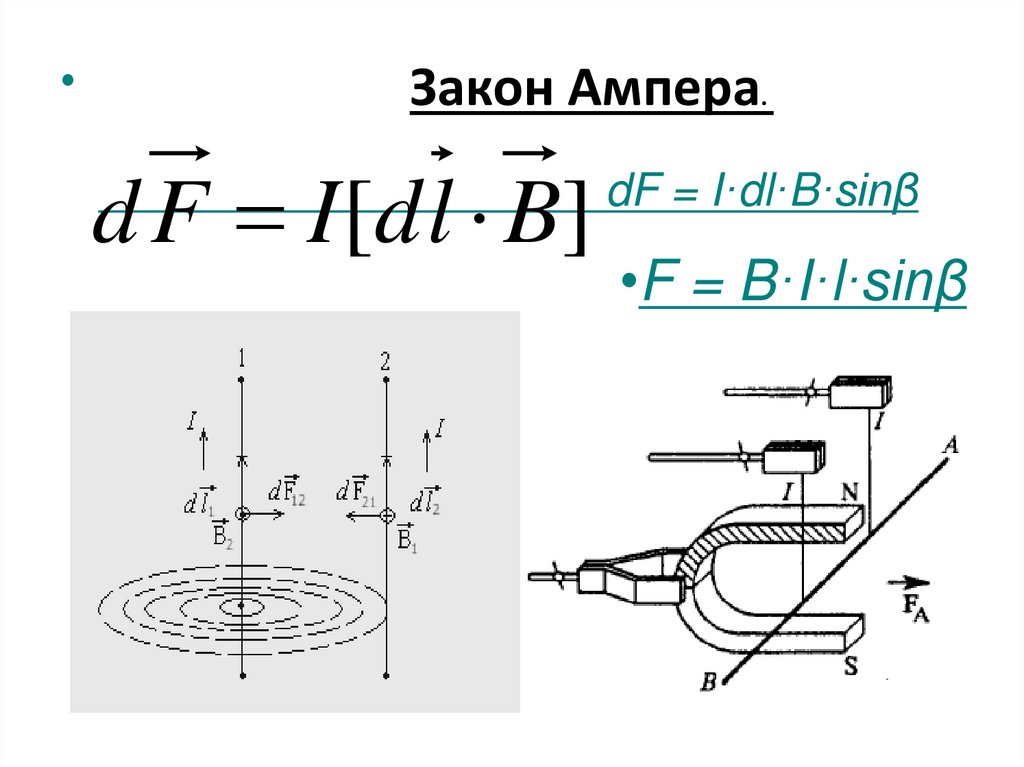
Закон Ампера.
d F I [d l B]
dF = I·dl·B·sinβ
•F = B·I·l·sinβ
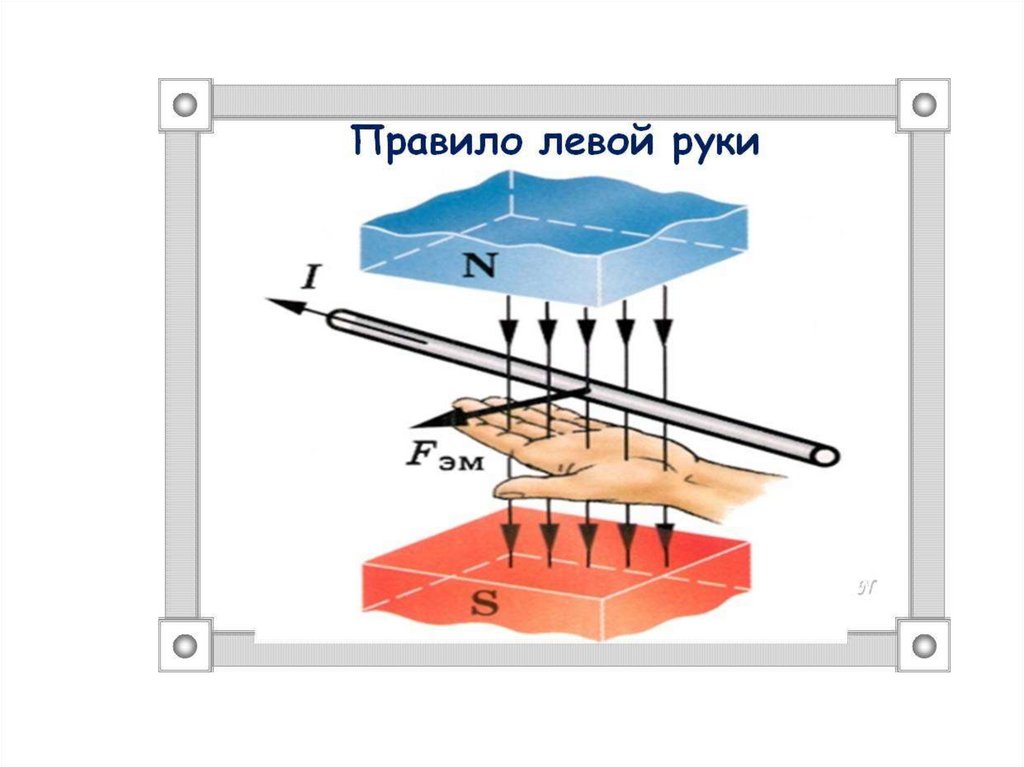
9.
10.
11.
12.
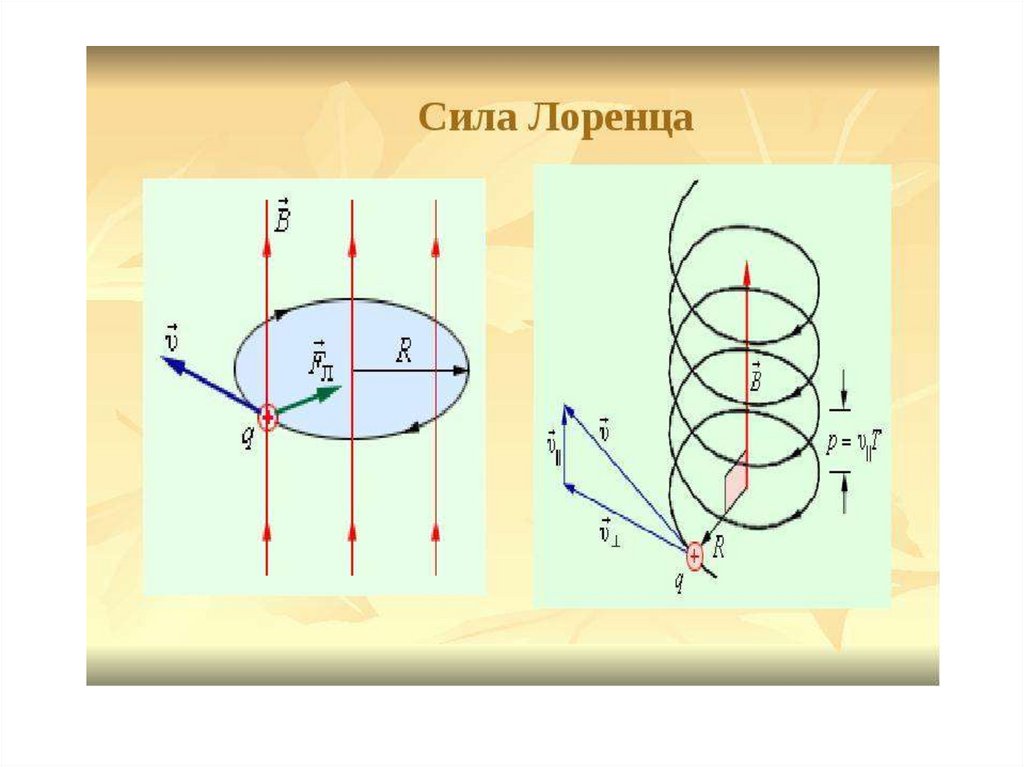
Сила Лоренца.F q[ V B ]
F = q·V·B·sin
Сила Лоренца не совершает работу по
перемещению заряда. А только искривляет
траекторию, т.е. заставляет заряды крутиться по
винтовой линии.
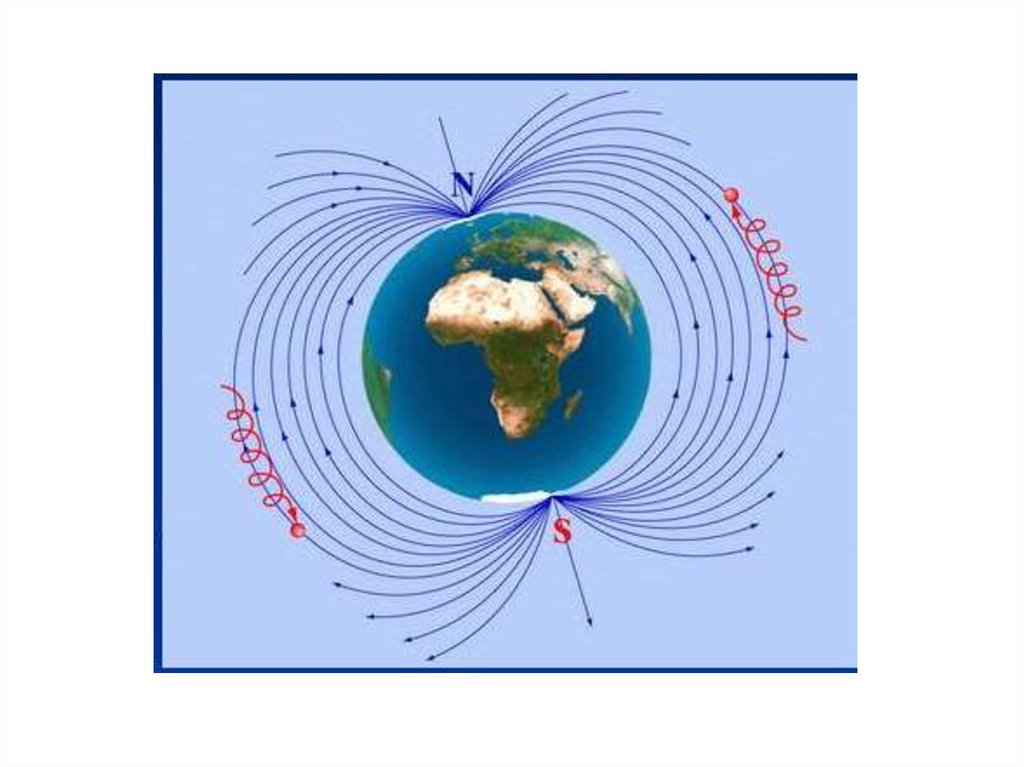
•20. Сила Лоренца разделяет заряды (сортирует)
•10.
по знакам.
13.
14.
15.
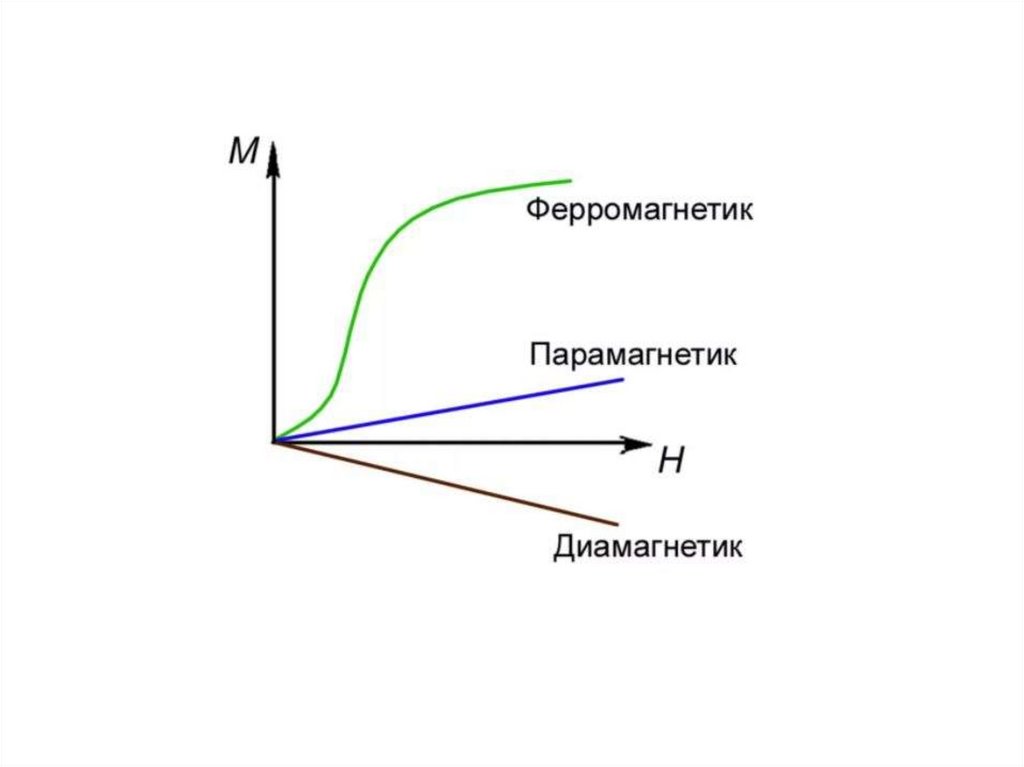
Магнетики: Диамагнетики.Парамагнетики.
Ферромагнетики.
16.
Диамагнетики – магнитные вещества, укоторых восприимчивость отрицательна
(магнитная проницаемость - <1).
Таблица. Магнитная проницаемость пара- и диамагнетиков.
Парамагнетики μ Алюминий 1,000021
Воздух 1,000004 Эбонит 1,000014 Платина 1,00026
Диамагнетики μ
Висмут 0,99984 Вода 0,999991 Медь 0,9999904 Стекло 0,999987
17.
Восприимчивость диамагнетиков:1
pm [ r j ]
2
j ZneV
1
pm r j sin
2
V r
2 2
Nze a H
M
6m
1
pm r j
2
eH
2m
e2a 2 H
pm e
6m
2
Nze a
d
6m
2
18.
19.
Восприимчивость парамагнетиков:Алюминий 1,000021, Воздух 1,000004 Эбонит 1,000014 Платина 1,00026
dF
M
dH
F = -NkT· lnz
2
z d e
0
z 2 e
0
H cos
kT
sin d
0
H cos
kT
d (cos )
20.
21.
z 2 eH
kT
H cos
kT
d (cos )
0
a
cos = x
2 ax
z
e d ( xa )
a 1
4
1
z
a
sha
22.
4F NkT ln
sha
a
dF dF
M
dH
kT da
dH
kT
da
1
M N ctha
a
H
kT
a
23.
MHa
1
kT
1 a
ctha
a 3
M
N
N
2
3kT
3
a
p
N
2
3kT
H
24.
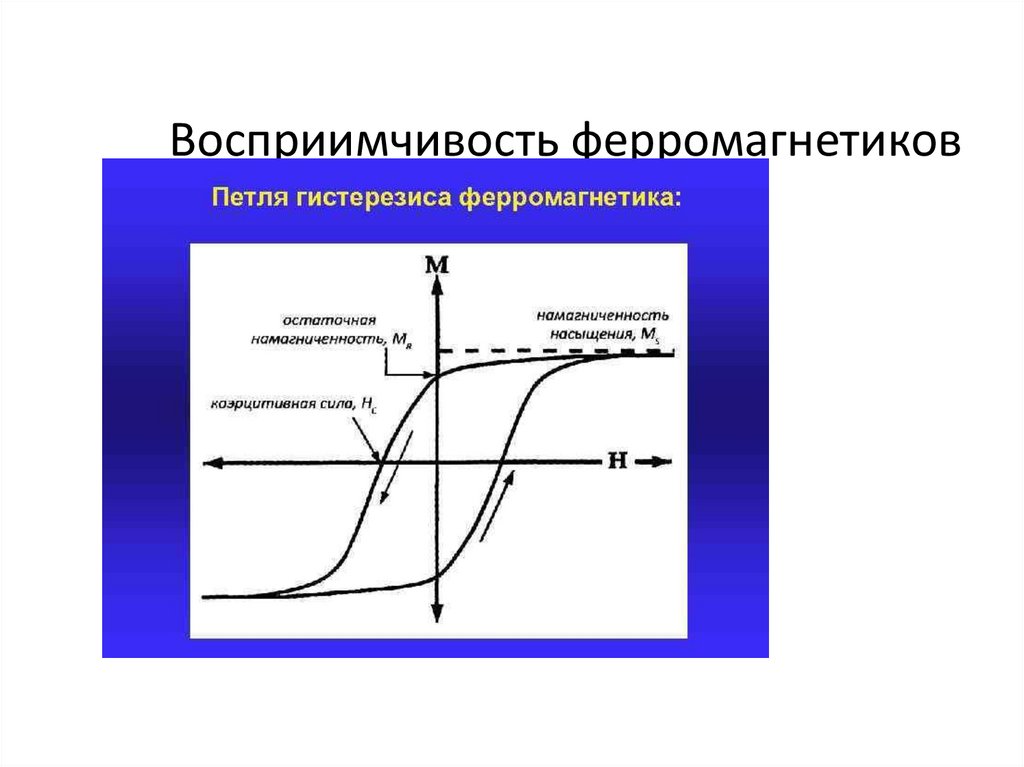
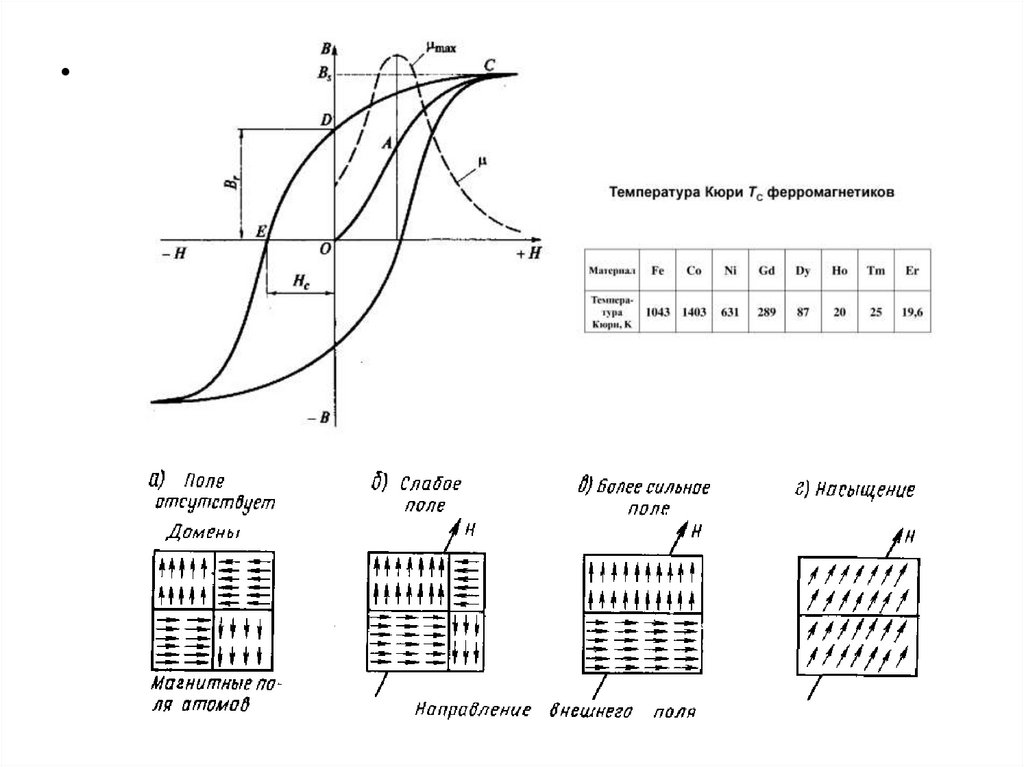
Восприимчивость ферромагнетиков25.
26.
27.
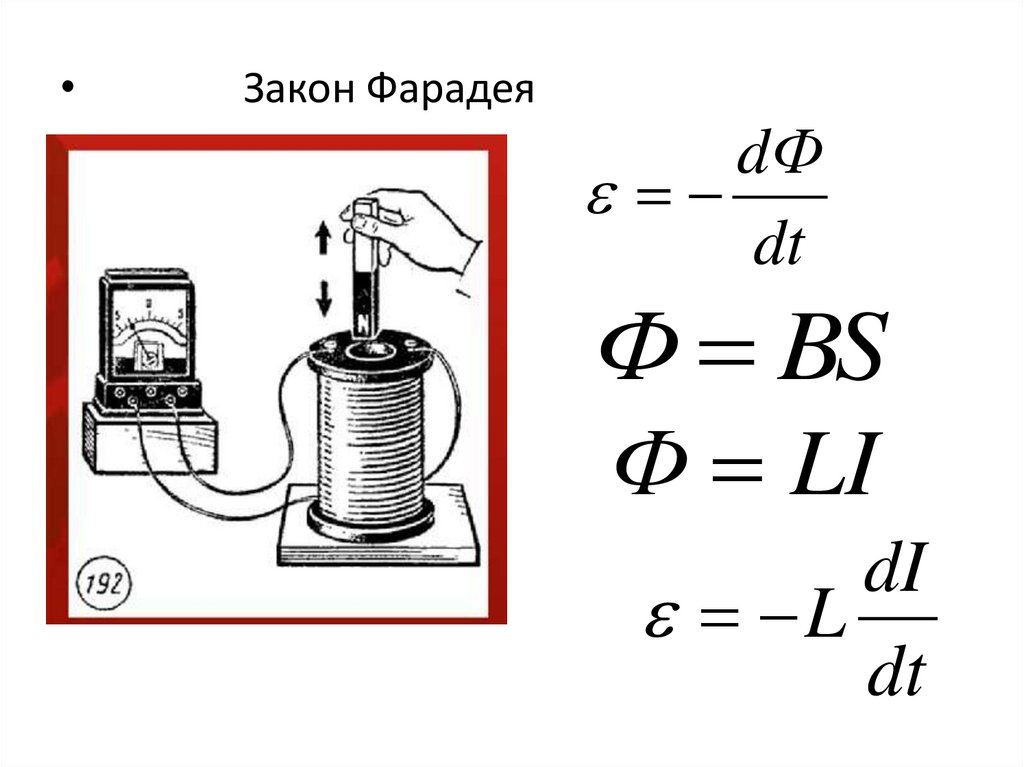
Закон Фарадея
dФ
dt
Ф BS
Ф LI
dI
L
dt
28.
dФdt
dФ BdS
S
Ф B S cos
29.
• Общая формула с источником тока(замыкание цепи)
dI
IR L
dt
u IR
dI
IR L
dt
L d ( IR )
IR
R
dt
30.
L d ( IR )IR
R
dt
d ( IR )
R
dt
IR
L
I
R
(1 e
R
t
L
)
I I 0 (1 e
R
t
L
)
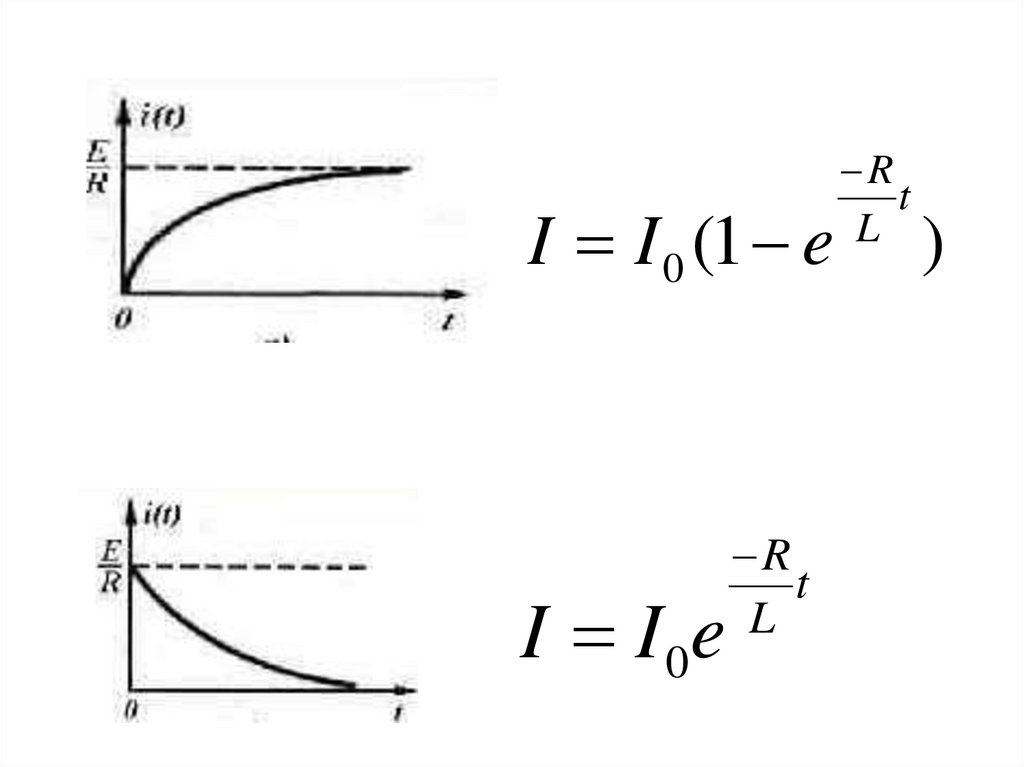
31.
• Размыкание цепиdI
IR L
dt
dI
R
dt
I
L
I I 0e
R
t
L
32.
I I 0 (1 eI I 0e
R
t
L
R
t
L
)
33.
Уравнения Максвелла
в дифференциальной форме
B
rotE
t
D
rotH
j
t
div D
divB 0
34.
35.
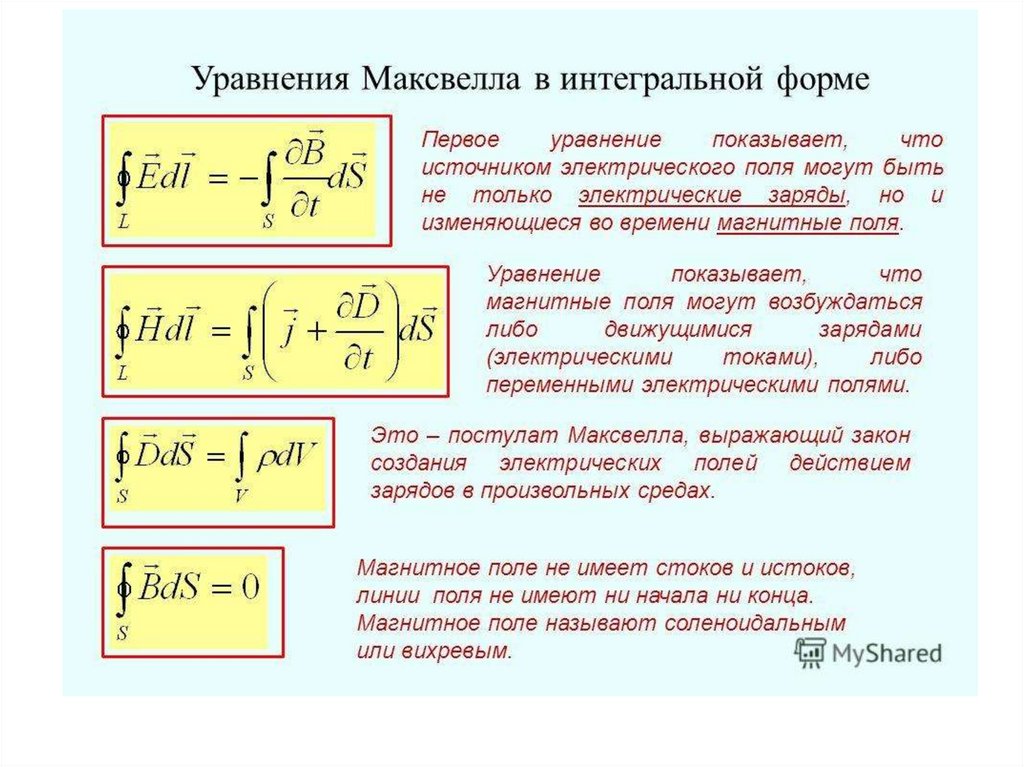
Уравнения Максвелла
в интегральной форме
B
L EdL S t dS
D
L HdL S ( j t )dS
DdS dV
S
V
BdS 0
S
36.
37.
irotE
x
Ex
j
y
Ey
k
z
Ez
Bx By Bz
divB
x
y
z
38.
Свободные колебания.m x Fx
Fx kx
m x kx
m x kx 0
x 0 x 0
x A sin( 0t )
2
k
2
0
m
39.
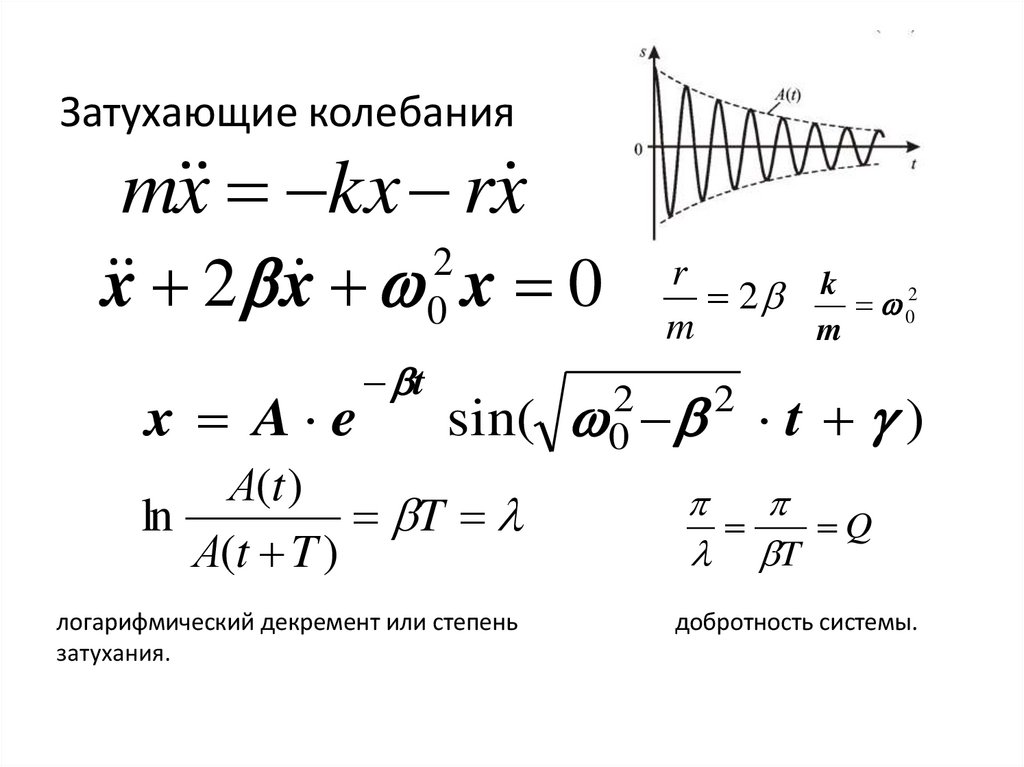
Затухающие колебанияm x kx rx
2
x 2 x 0 x 0
x A e
t
sin(
А(t )
ln
T
А(t T )
логарифмический декремент или степень
затухания.
r
2 k 02
m
m
2
2
0 t )
Q
T
добротность системы.
40.
• Вынужденные колебания.i t
m x kx rx F0 e
2
i t
x 2 x 0 x f 0e
x x1 x2
x1 A e
t
x2 a e
e
i t
sin(
i 1
2
2
0 t )
i t
cos( t ) i sin( t )
41.
̂x ia ei t2
xˆ a 2 2 ei t
2
i t
i t
aˆ e 2 iaˆ e
2
i t
aˆ e f 0 e
2
0
i t
a ( i 2 ) f 0
2
2
0
42.
f0a 2
2
( 0 ) i 2
( ) i 2 e
2
0
2
( ) 4
2
0
2 2
2
2
arctg 2
2
0
i
2
43.
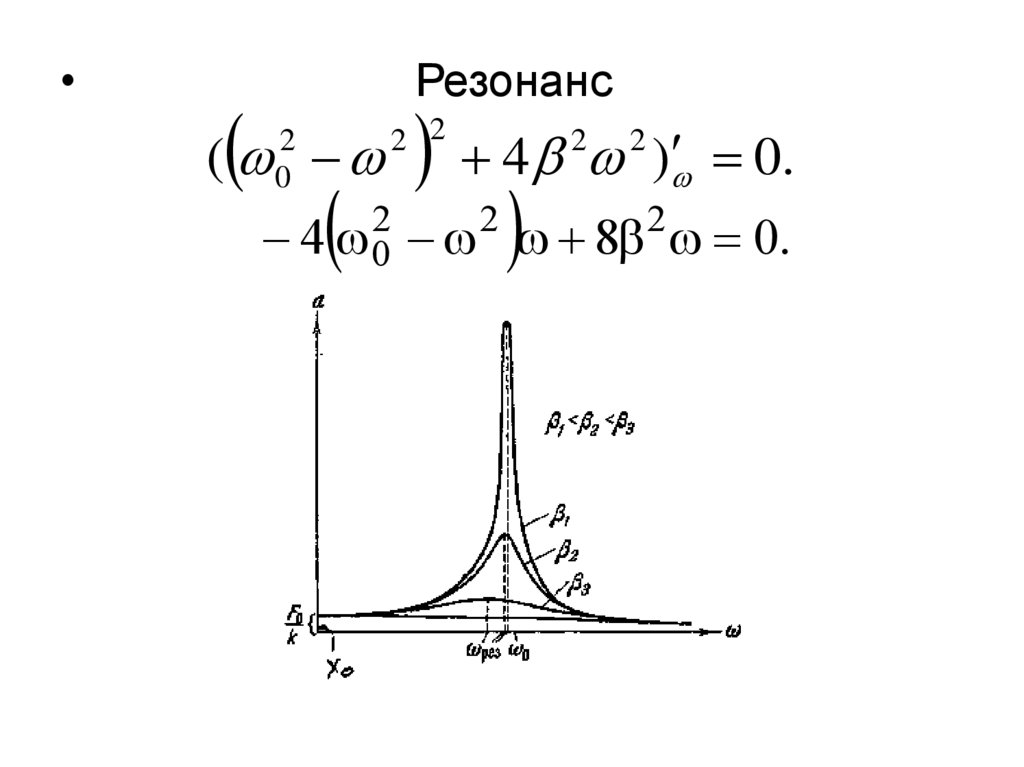
Резонанс
(
2
0
4 ) 0.
2 2
2
2
2
2
2
4 0 8 0.
44.
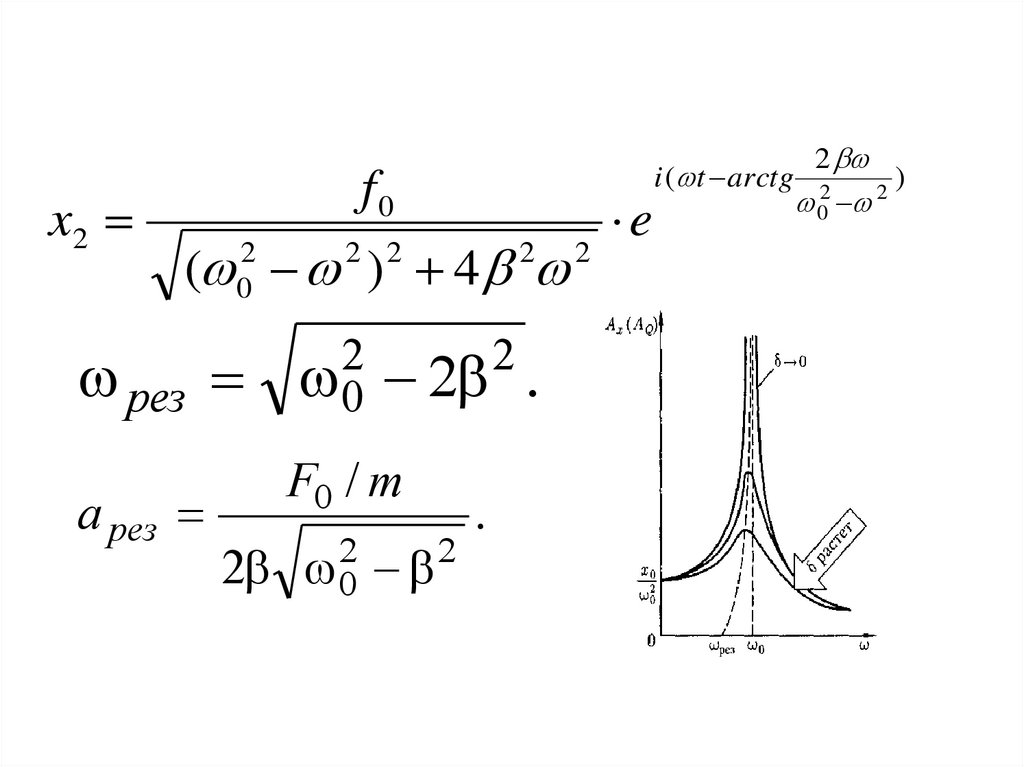
x2f0
( ) 4
2
0
рез
a рез
2 2
2
2
0 2 .
F0 / m
2
2
2
2
0
.
2
e
i ( t arctg
2
)
2
2
0
45.
Волновое уравнение. Фазовая и групповая скорости.
2 2 2
1 2
2 2 2 2
2
x
y
z
V t
1
2
2
V t
2
Уравнение плоской волны
( x, t ) Ae
i ( t kx 0 )
( x, t ) A cos( t kx 0 )
46.
Vфазов ое
k
2
T
k
2
dx d
Vгруппов ое
dt dk
Уравнение сферической волны
A0
( x, t )
cos( t kx 0 )
r
47.
Волновая оптика.Уравнение волны:
x A cos t k r
Интерференция, дифракция,
поляризация.
48.
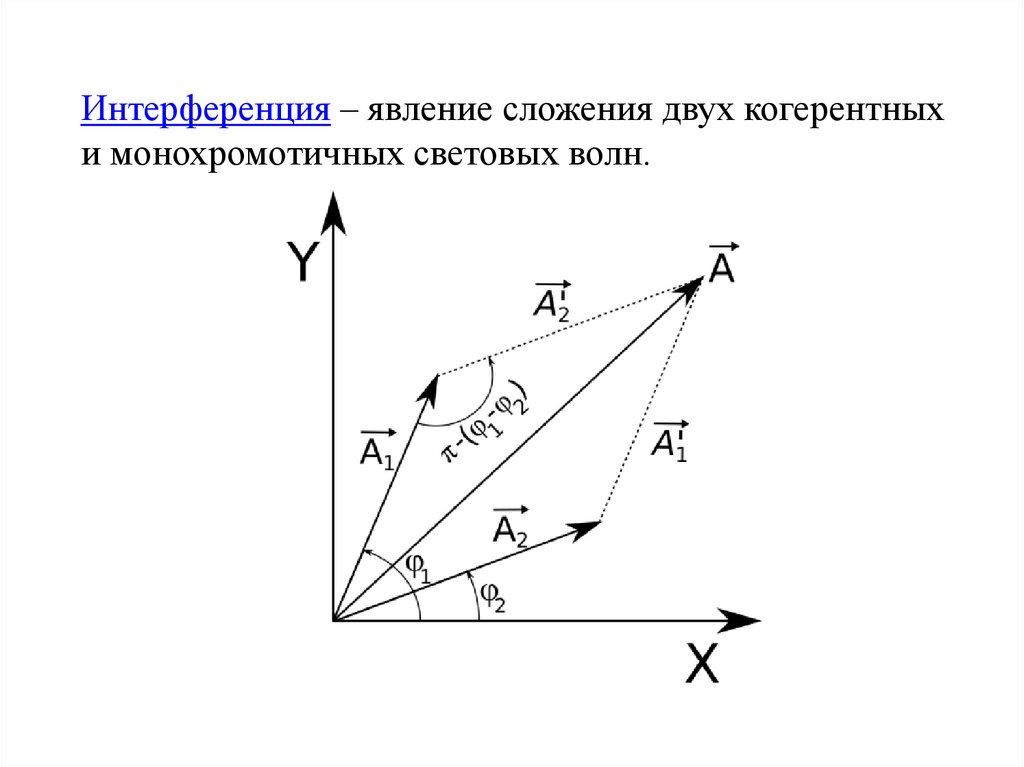
Интерференция – явление сложения двух когерентныхи монохромотичных световых волн.
49.
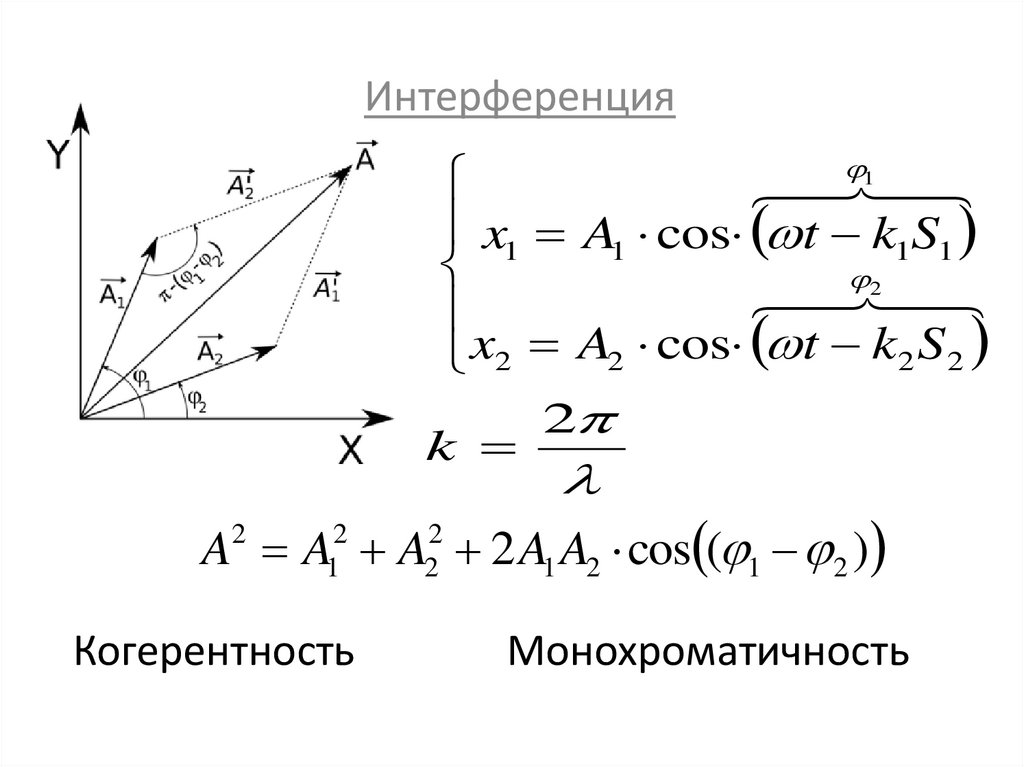
Интерференция1
x1 A1 cos t k1S1
2
x2 A2 cos t k2 S 2
2
k
A A A 2 A1 A2 cos ( 1 2 )
2
2
1
Когерентность
2
2
Монохроматичность
50.
A Amax1 2 2 m (2m)
A Amin
1 2 2 m (2m 1)
1 2 k 2 S 2 k1 S1
c
n
uФ
c
n2 S 2 n1 S1
uФ
– оптическая разность хода
k
2
0
51.
= n2 S2 – n1S1max = 2m· о 2 – условие max
min = (2m+1)· о 2– условие min
интерференционной картины.
52.
53.
Расчет интерференционной картины от двухисточников.
54.
=s2—s1
d 2
s l (x )
2
d 2
s l (x )
2
s 22 s12 2 xd
s2 s1
2
2
2
2
1
xd
l
2
2 xd
s1 s2
55.
xmax 2m0 l
, m 0,1,2,...
2 d
xmin (2m 1)
0 l
2 d
ширина интерференционной полосы, равно
l
x 0
d
56.
Интерференция света на тонких пленках57.
:= n2 S2 – n1S1
1 и 2 , в, n – известны.
S1 ; S2 - ?
Из АDВ:
,
cos 2
2в
2в
S2
S2
cos 2
Из АЕС
S1
S1
sin 1
AC 2 DC
DC из ВDC:
DC
tg 2
в
DC в tg 2
58.
S1sin 1
2в tg 2
S1 = 2в tg 2·sin 1
2в
n
2в tg 2 sin 1
cos 2
sin 1
n
sin 2
sin 1 n sin 2
59.
2nвsin 2
2в
sin 1
cos 2
sin 2
1
sin 2 2
2вn cos 2
2вn
cos 2 cos 2
1
2
2
2вn 1 sin 2 2вn 1 2 sin 1 2в n sin 1 0
n
2
2
0
2в n sin 1
2
0
0
MAX 2m
MIN (2m 1)
2
2
2
2
60.
rmin m 0 Rrmax (2m 1) 0 / 2 R
61.
Дифракция
= d·sin
MAX 2m
0
2
MIN (2m 1)
;
0
2
62.
63.
Вычисление для щели:
= b·sin
i ( t k )
dE dA e
= x·sin
А0
dA
dx
b
64.
A0 i t ikx sindE
e e
dx
b
b/2
b/2
A0 i t
E
e e ikx sin dx c1 e
b
b / 2
b / 2
b/2
i b
i 2 x sin
c1
c1 (e e
2 i x
e
2i
2
i
b / 2
i b
dx
)
65.
i be e
2i
i b
sin( b)
E с2 sin( b)
Для min дифракционной картины Е = 0,
т.е.
sin( b) = 0;
b = m
66.
sin b mb·sin = m – условие min.
67.
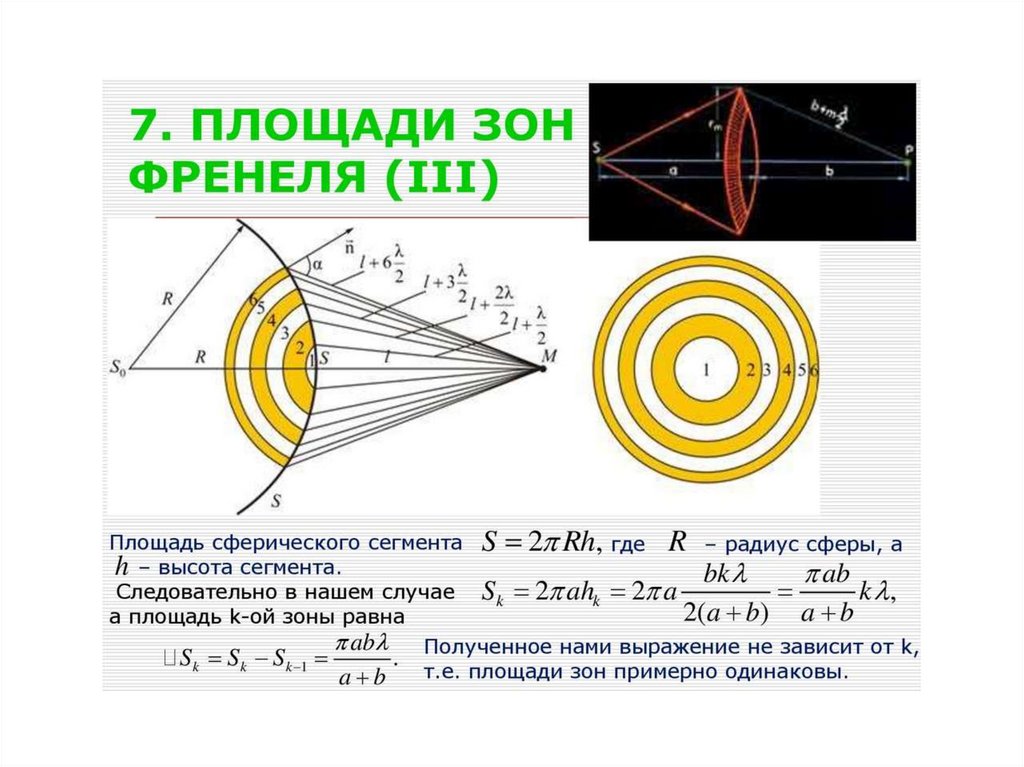
Метод зон Френеля68.
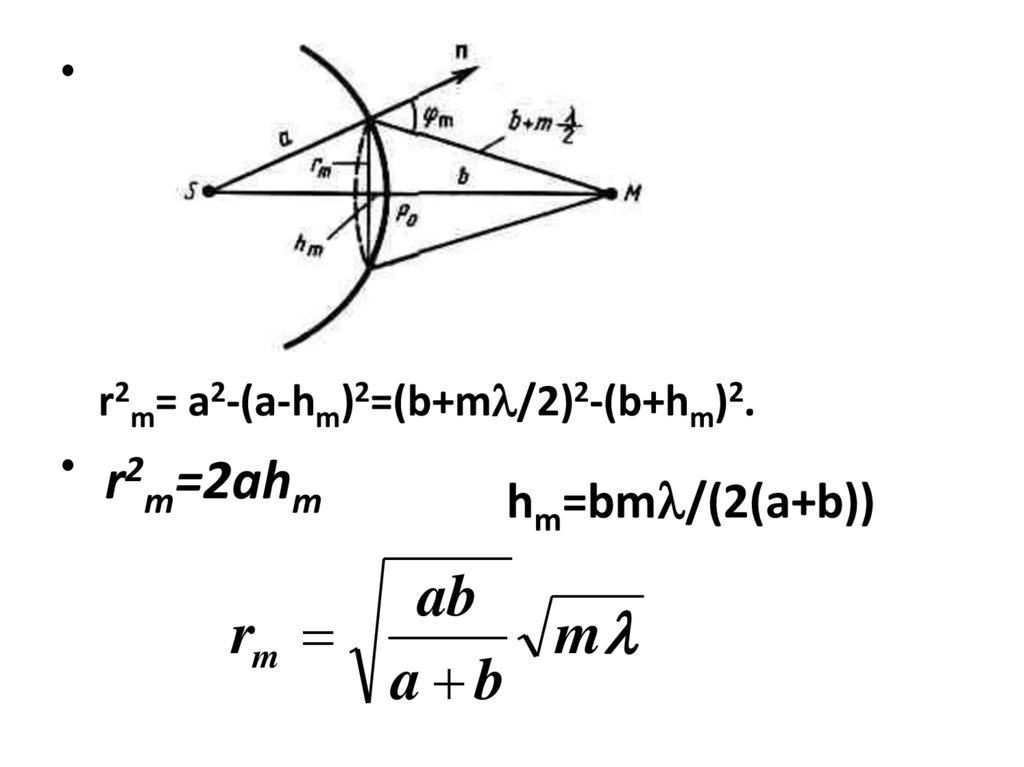
r2m= а2-(а-hm)2=(b+m /2)2-(b+hm)2.
• r2 =2ah
m
m
hm=bm /(2(a+b))
ab
rm
m
a b
69.
70.
Поляризацияtg бр n
71.
72.
73.
Формула Планка. Закон Вина, Стефана– Больцмана.Закон Вина
4 h
1
r
2
h
c
c
e kT 1
3
b
MAX
T
b 2,9 *10 3 м * К
Стефана – Больцмана
R T
4
5,67 *10 8 Вт /( м2 * К 4 )
74.
75.
Масса и импульс фотона.
h
h
m 2
c
c
0
h h
p
c
c
де- Бройлевская длина волны
h
h
p mV
76.
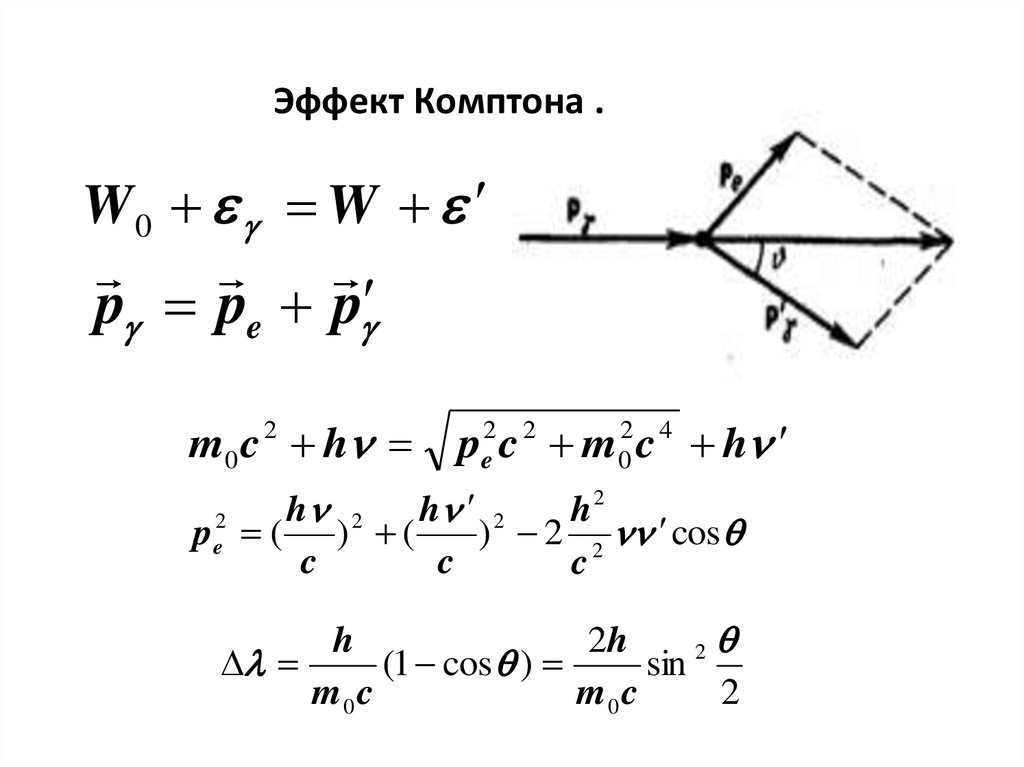
Эффект Комптона .W0 W
p pe p
m0 c 2 h
pe2 c 2 m02 c 4 h
2
h
h
h
pe2 ( ) 2 (
) 2 2 2 cos
c
c
c
h
2h
2
(1 cos )
sin
m0c
m0c
2
77.
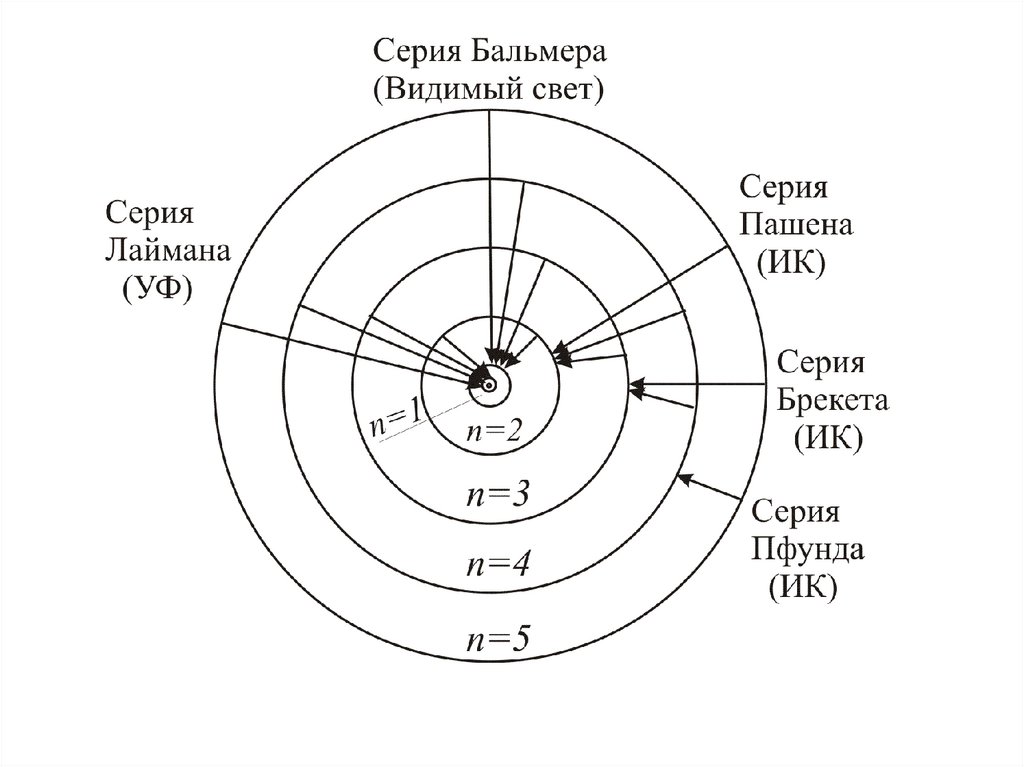
Теория атома водорода по Бору.h
Постулаты Бора.
Ze
2
2
2
mV
2
r
4 0 r
2
2 4 0
rn n
mZe 2
mVr n (n 1,2,3,...)
1 Z 2 me4
En 2
(n 1,2,3,....)
2 2
n 8h 0
mn h mn En Em
me4 1
1
mn 3 2 ( 2 2 )
8h 0 m n
78.
Серия Лаймана:c
Серия Бальмера
79.
80.
Элементымеханики.
p k
h
x px h
y p y h
атомной
физики
E h h
и
квантовой
h
2
c
E t h
z pz h
dW dV
2
dV 1
2
81.
Уравнение Шредингера в общем виде.U ( x, y, z, t ) i
2m
t
2
2 2 2
x
y
z
2
2
Ae
2
i 1
—оператор Лапласа
i
( Et px )
волновая функция.
82.
Движение свободной частицы.2m
2 ( E U ) 0
U 0
2m
2 E 0
2
x
2
i ( kx t )
Ae
2
2
2
x
k
p
E
2m 2m
83.
• Частица в одномерной прямоугольной«потенциальной яме» с бесконечно
высокими «стенками».
84.
2m2 ( E U ) 0
2
x
2
(0) (l ) 0
2 2m
2 E 0
2
x
U 0
2mE
k
2
2
2
k
0
2
x
2
( x ) A sin( kx ) B cos( kx )
85.
( x ) A sin( kx ) B cos( kx )т.к. (0)=0, то В=0.
( x) A sin( kx)
(l ) 0
A sin( kl) 0
n
k
l
n
n ( x) A sin(
x)
l
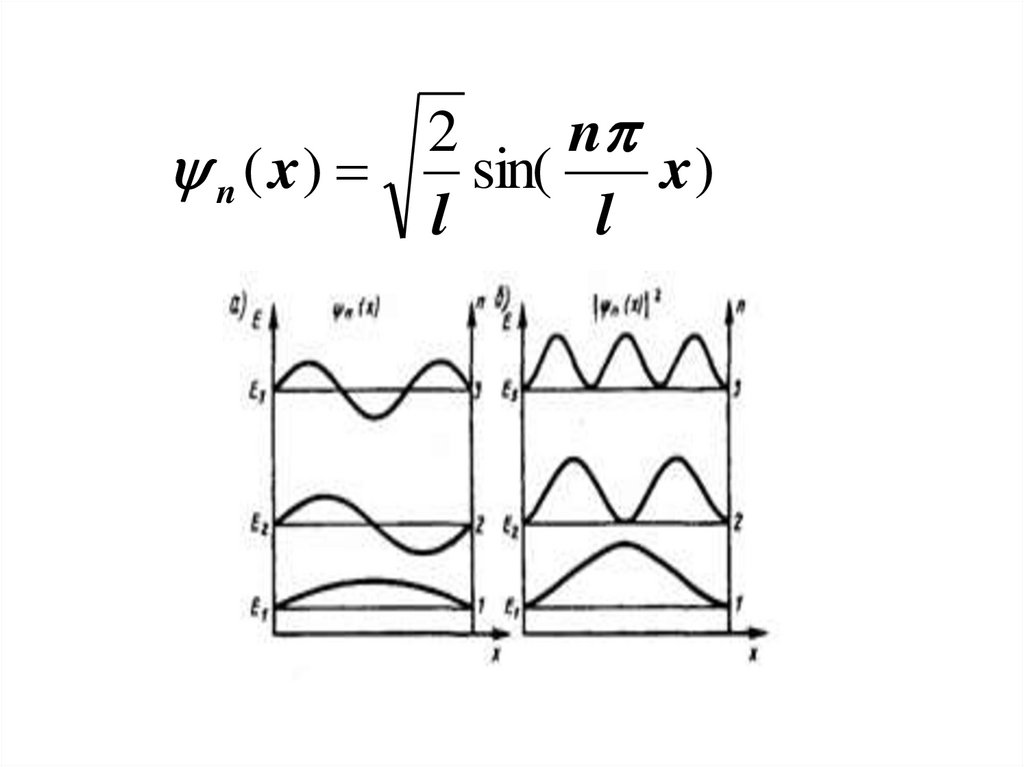
86.
2n
n ( x)
sin(
x)
l
l
87.
88.
22m
ze
2 ( E
) 0
4 0 r
2m
m x
2 (E
) 0
2
x
2
2
2
0
2
2m
2 E 0
2
x
2
U ( x, y, z, t ) i
2m
t
2m
2 ( E U ) 0
2
89.
90.
Полная система квантовых чисел. ПринципПаули. К-, L-, М- оболочки атома.
Заполнение электронных оболочек
периодическая система элементов.
Состояние электрона в атоме однозначно
определяется набором четырех квантовых чисел:
главного n (n=1, 2, 3, ...),
орбитального l (l=0, 1, 2, ..., n-1),
магнитного ml (ml= -l,..., -1, 0, + 1, ..., +l),
магнитного спинового ms (ms= +1/2, -1/2).
и
91.
Квантовые числа n и l характеризуют размери форму электронного облака, а квантовое
число
ml
характеризует
ориентацию
электронного облака в пространстве.
2
4
1 Z me
En 2
(n 1,2.3,....)
2 2
n 8h 0
Le h l (l 1)
l 0,1,....(n 1)
Lez hml
ml 0, 1,.., l
92.
Z n 2n2
Zl 2(2l 1)
93.
Распределения Бозе-Эйнштейнаи
Ферми-Дирака.
1
Ni
e
Ei
kT
1
1
Ni
e
Ei
kT
1
94.
• Зонная теория твердых тел.95.
96.
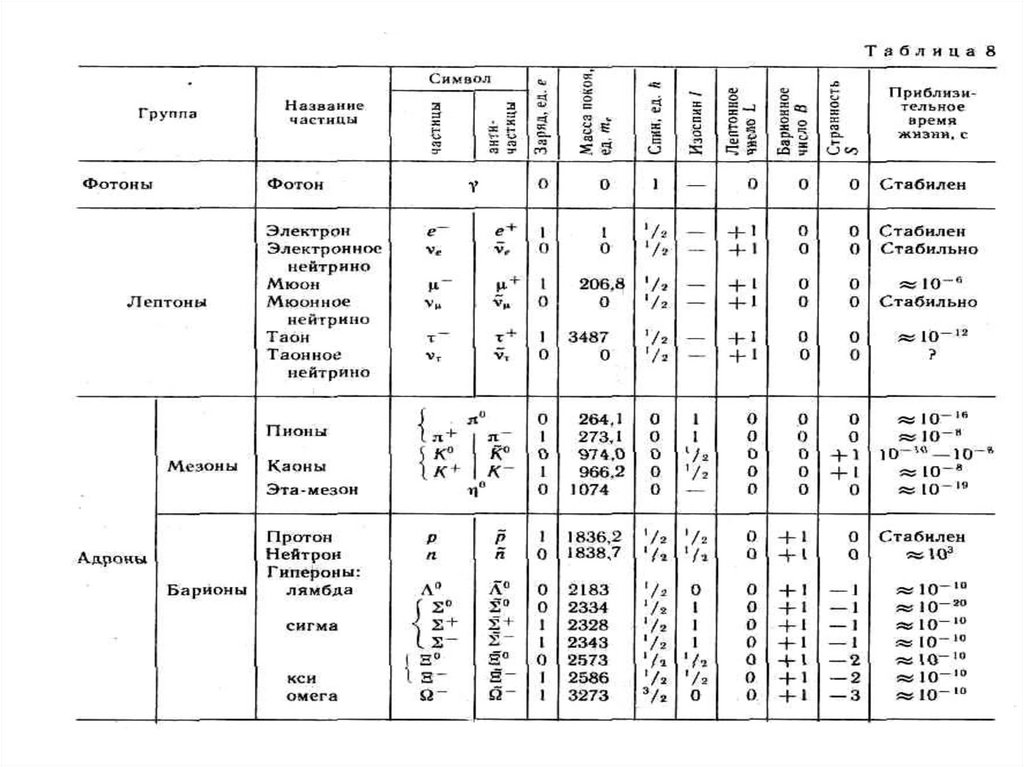
Строение атомного ядра.Протон (р) имеет положительный заряд,
равный заряду электрона, и массу покоя
mp=1,6726•10-27 кг 1836me, где me — масса
электрона.
Нейтрон (n) — нейтральная частица с
массой покоя mn=1,6749•10-27кг 1839me,. Протоны
и нейтроны называются нуклонами (от лат.
nucleus
—
ядро).
Общее число нуклонов в атомном ядре называется
массовым числом
А.
A
Z
X
97.
• Размер ядра. Дефект масс и энергиясвязи ядра. Удельная энергия связи.
R =R0A1/3,где R0=(1,3—1,7) 10-15м.
Eсв=[Zmp + (A-Z)mn-mя]c2,
Eсв=[ZmH + (A-Z)mn-m]c2
98.
-, - и -излучение.A
Z
X ZA 42Y 24He
234
U 90
Th 24He
238
92
A
Z
X Y e ~
A
Z 1
0
1
0
~
Th 234
Pa
e
91
1
1
1
0
~
n p e
234
90
0
1
1
A
Z
X Z A1Y 10e
13
7
N 136C 10e
1
1
p 01n 10e
99.
100.
101.
102.
103.
lt
u
eE l
V
2m u
ne E l
j ne V
2m u
2
j E
ne l
2 m u
2
104.
• Закон Джоуля — Ленца. К концу свободногопробега электрон под действием поля приобретает
дополнительную кинетическую энергию
2
max
mV
Ek
2
e E l
2
2m u
2
2
2
За единицу времени электрон испытывает с узлами
решетки в среднем z столкновений:
u
Z
l
105.
• Если n — концентрация электронов, то в единицувремени происходит п z столкновений и решетке
передается энергия
W n Z Ek
энергия, передаваемая решетке в единице объема
проводника за единицу времени,
ne E l
W
2m u
2
2
106.
• Закон Видемана — Франца.Отношение теплопроводности к удельной
проводимости для всех металлов при одной и той же
температуре одинаково и увеличивается
пропорционально термодинамической температуре:
T
=3(k/e)2
107.
Правила Кирхгофа108.
109.
• Электромагнитные колебания110.
СВОБОДНЫЕ КОЛЕБАНИЯ( R=0 и источника нет )
Q 2 LI 2
W
const
2C
2
dW 2Q Q 2 LII
0
dt
2C
2
Q
0
LQ
C
111.
1Q
Q 0
LC
Q QMAX cos( 0t )
112.
ЗАТУХАЮЩИЕ КОЛЕБАНИЯ2
2
Q
LI
2
W
I Rt
2C
2
R
1
Q
Q
Q 0
L
LC
2
Q 2 Q 0 Q 0
113.
Q QMAX exp( t ) cos( t )2
1
R
2
LC 4 L
114.
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ2
2
Q
LI
2
I Rt IUt
2C
2
R
1
Um
Q Q
Q
cos t
L
LC
L
Um
2
Q 2 Q 0 Q
cos t
L
115.
U2 Q Q m cos t
Q
L
2
0
Q Qmax exp( t ) cos( t )
Um / L
( ) 4
2
0
2 2
2
2
cos( t )
116.
a резUm
L
2
2
0
2
.
рез 2 .
2
0
2














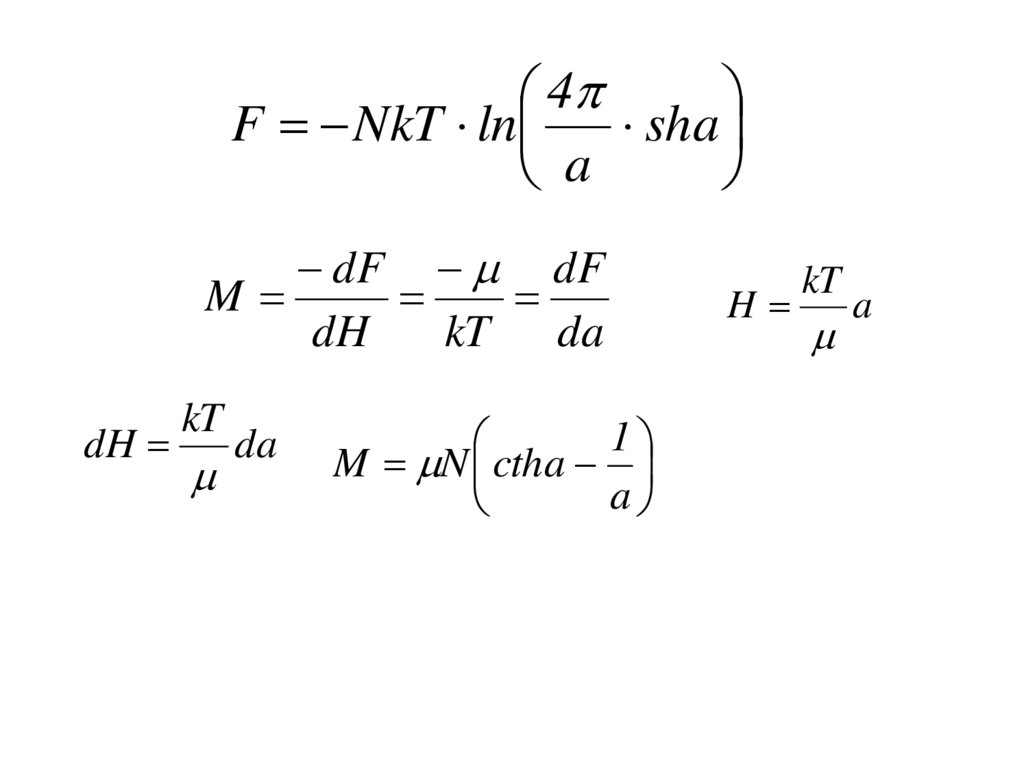



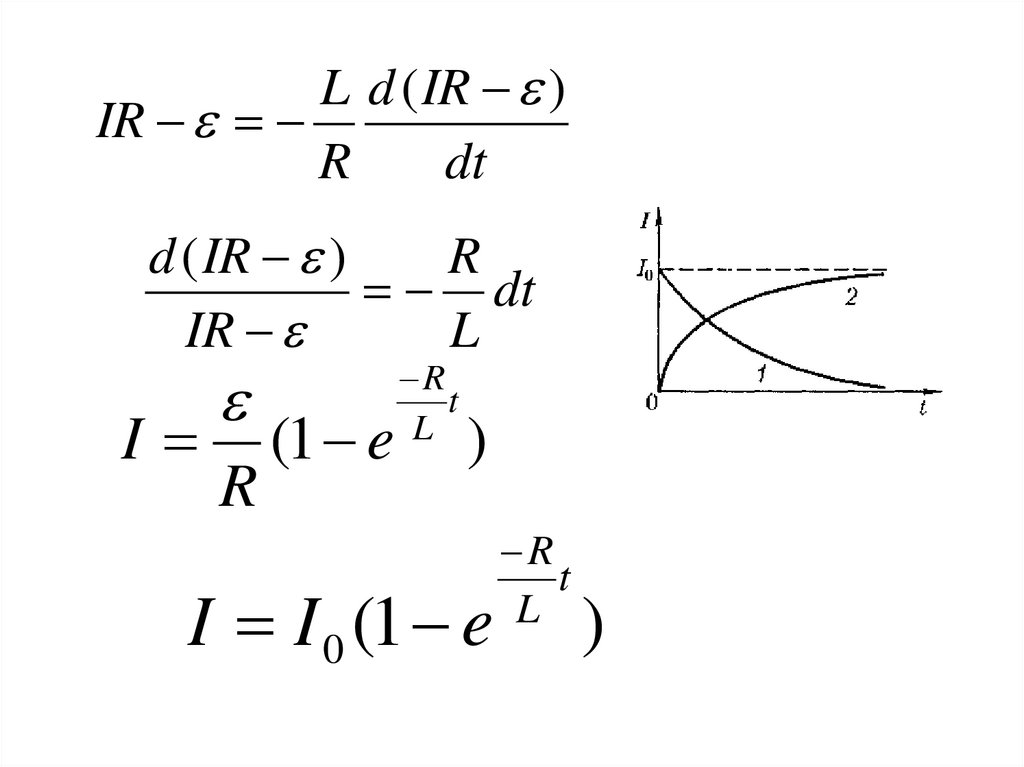




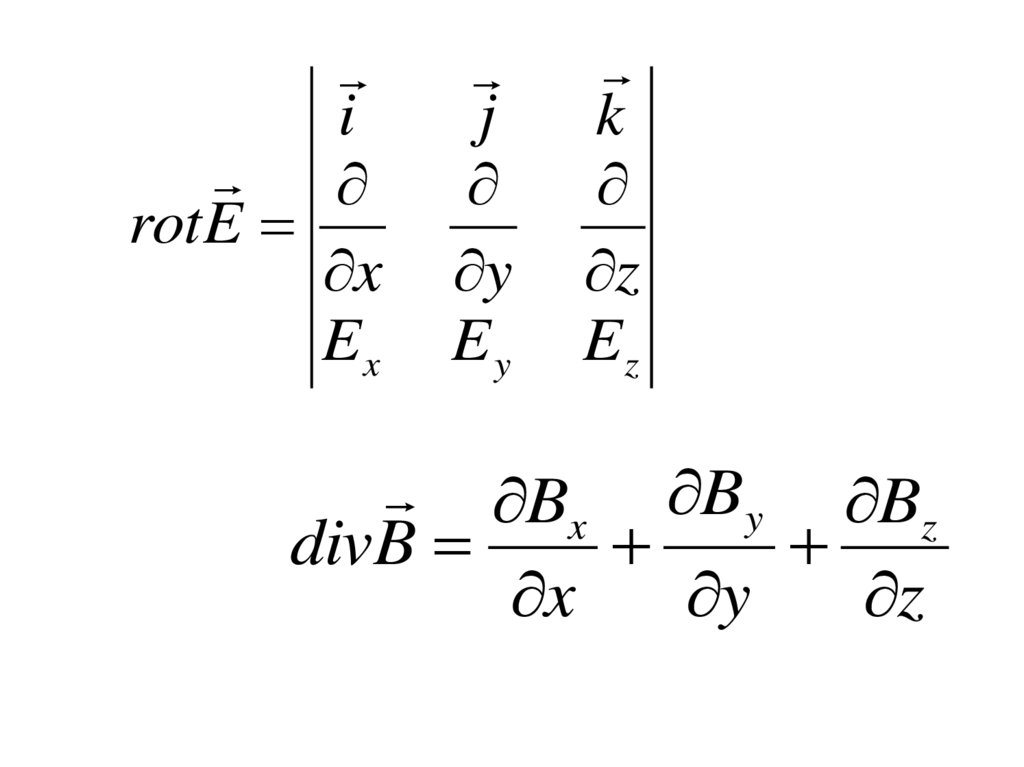



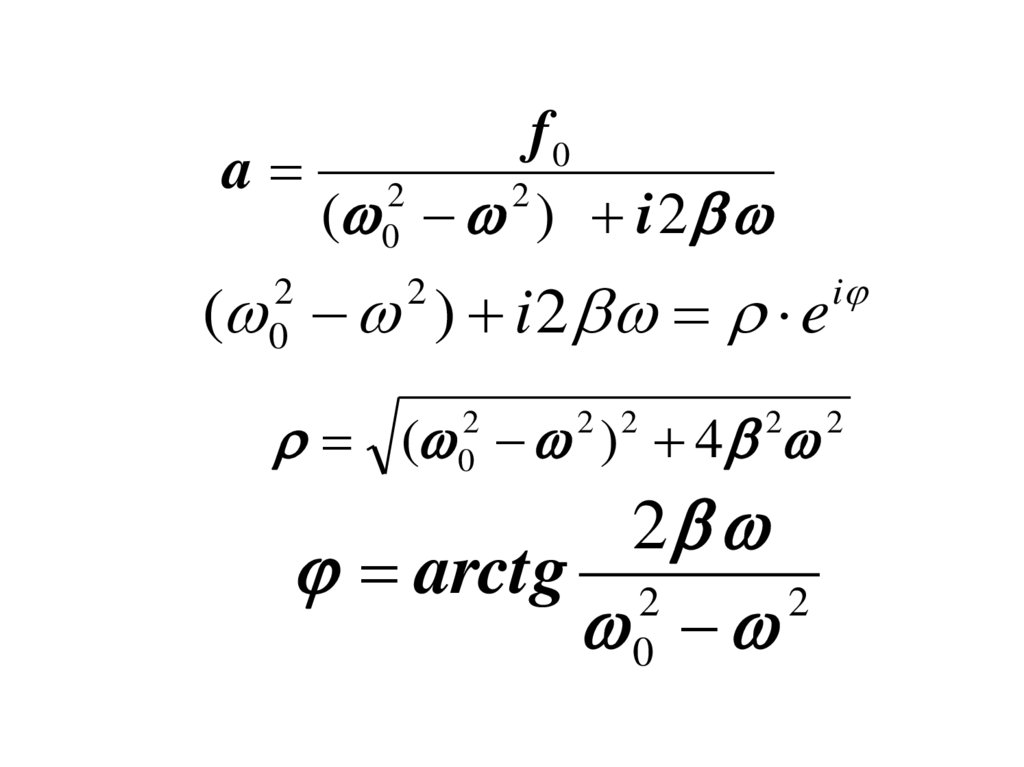











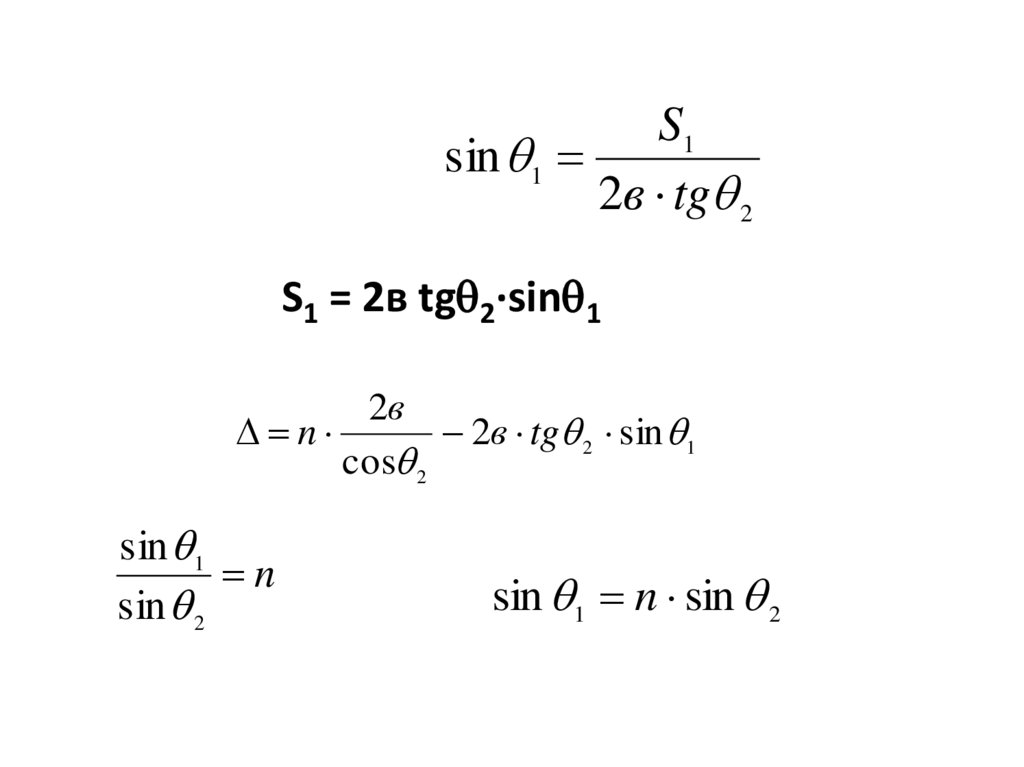
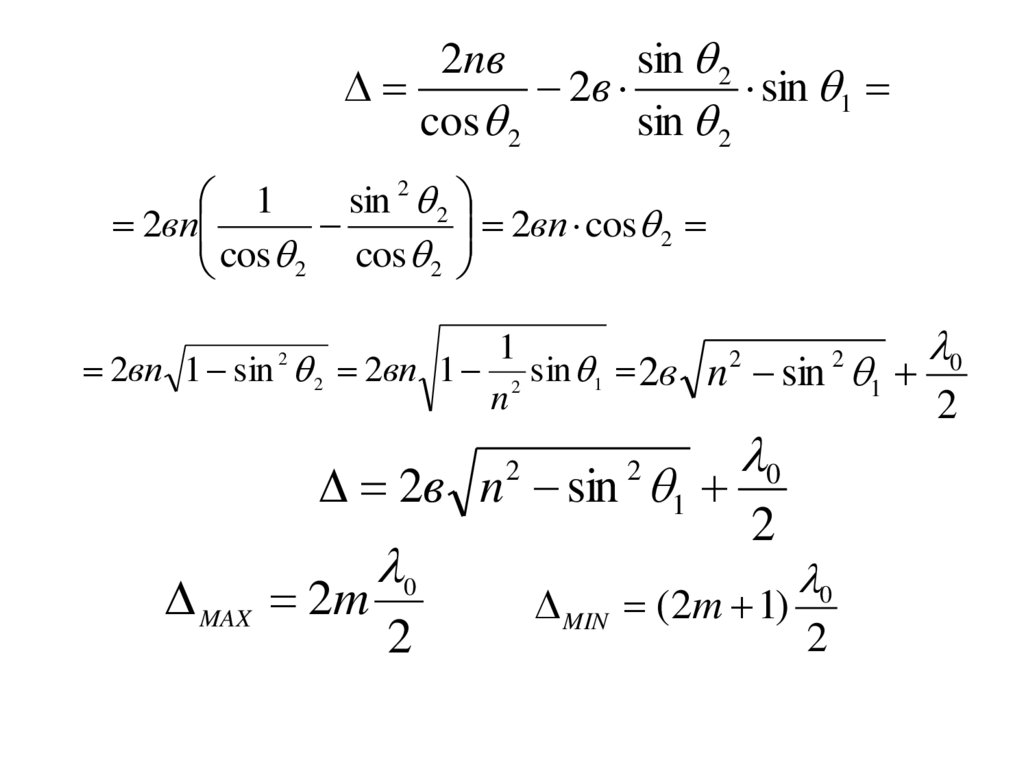





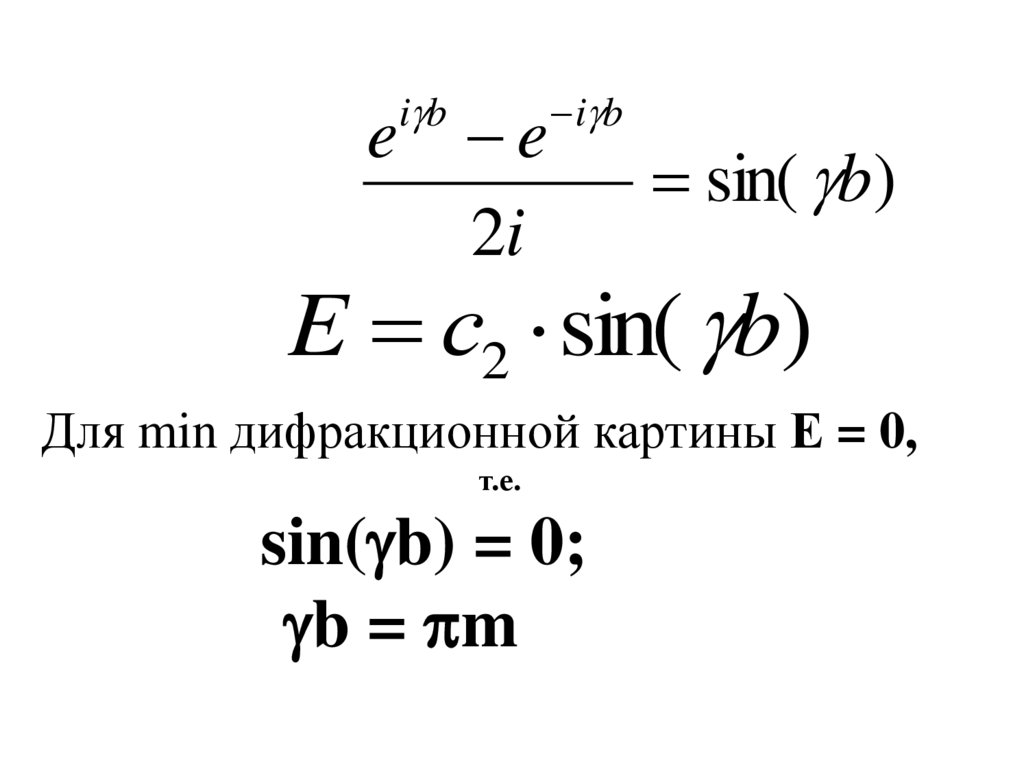
















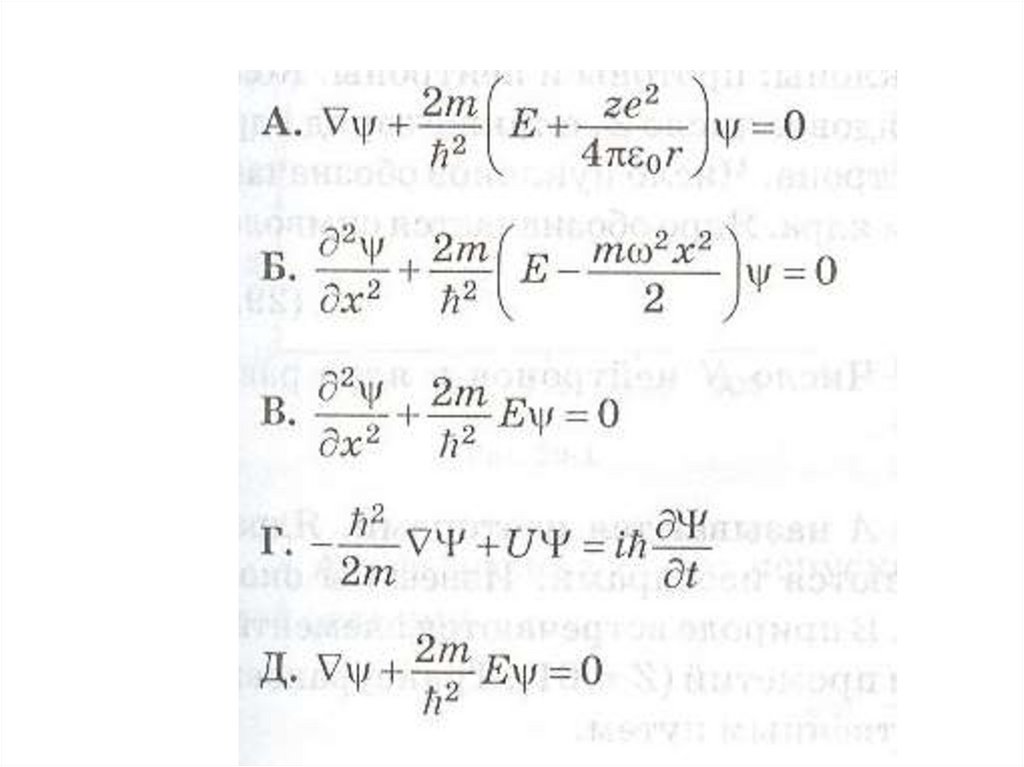











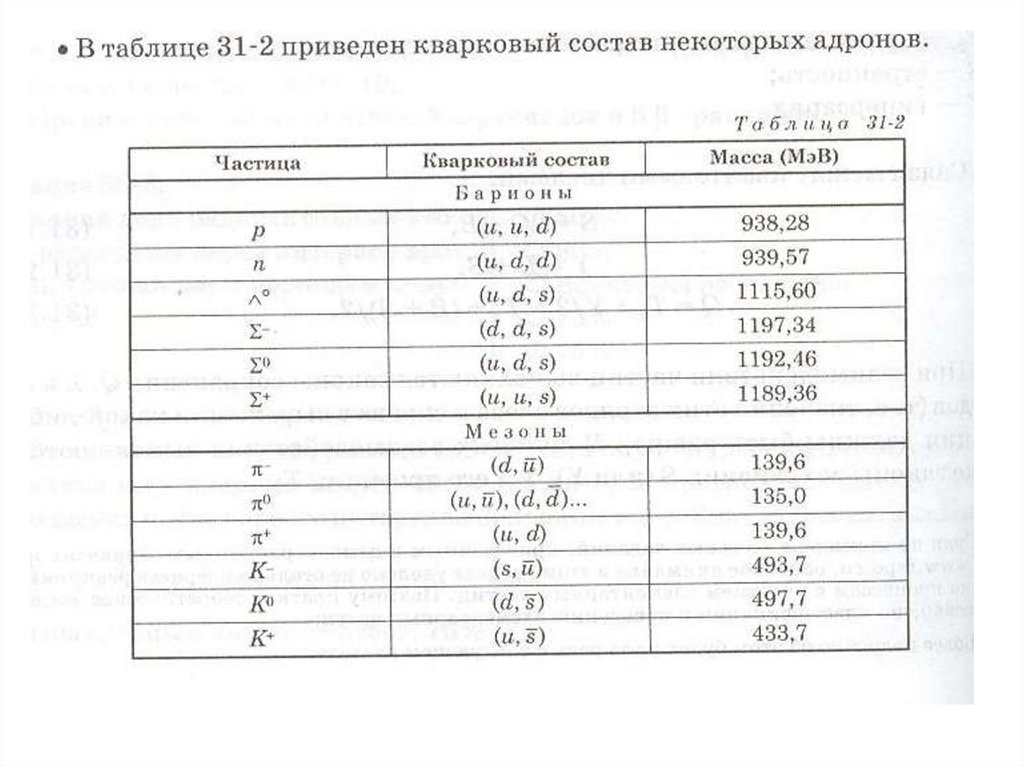


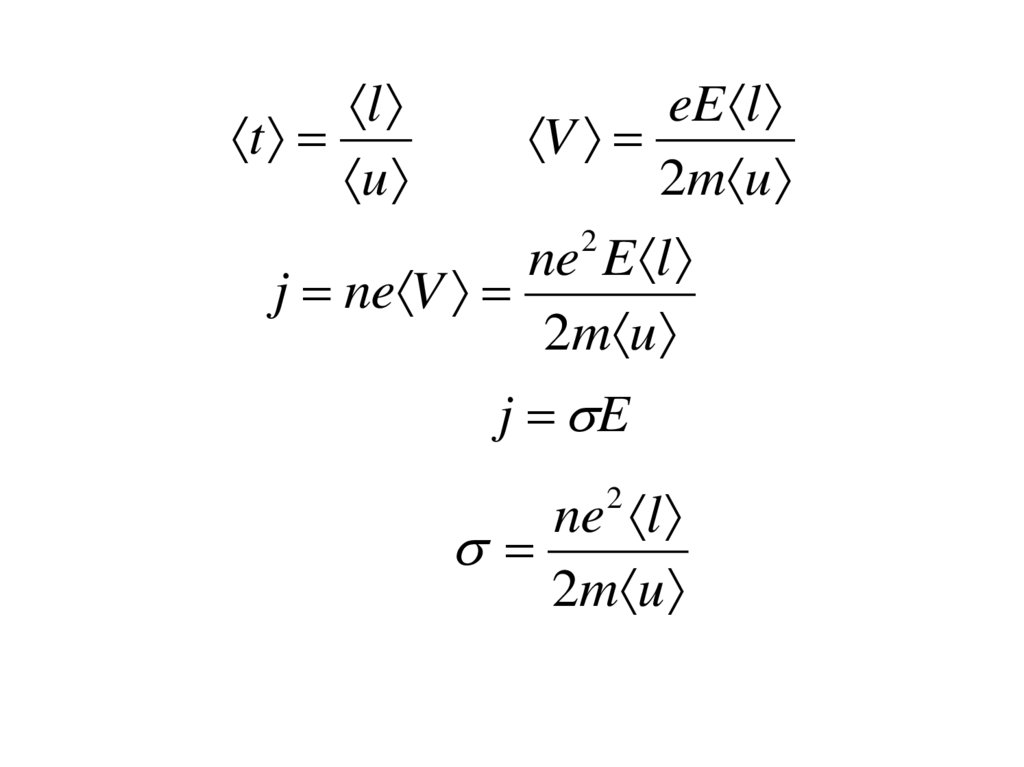











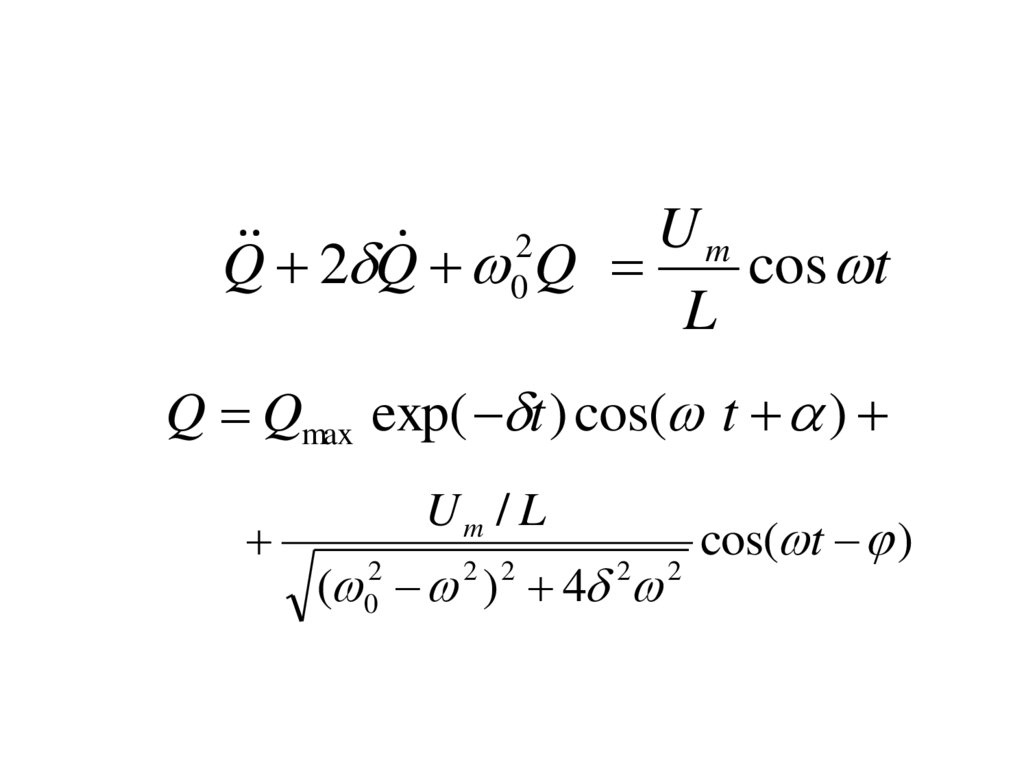

 Физика
Физика








