Плоские гармонические волны в неравновесных системах. (Лекция 9)

1.

Лекция 9.
Плоские гармонические волны в неравновесных системах
1. Волны в одномерном пучке электронов
а. Быстрая и медленная волны плотности заряда
б. Энергии импульсы волн плотности заряда пучка
2. Пучковая неустойчивость в плазме
а. Дисперсионное уравнение пучковой неустойчивости в плазме
б. Нерезонансная и резонансная пучково-плазменные неустойчивости
в. Начальная задача для волн в пучково-плазменной системе
г. Дифференциальное уравнение пучково-плазменного взаимодействия
3. Неустойчивость плазмы с током
а. Дисперсионное уравнение для частот волн в холодной плазме с током
б. Нерезонансная и резонансная неустойчивости Бунемана

2.

2
jb1
jb1 Lb
Ψ (t , z ) jb1 , jb 2 , E z j1 ( , k ), j2 ( , k ), ez ( , k ) exp( i t ikz )
u
E z 0,
t
z
4
2
2
2
jb 2
jb 2
jb1
i ( ku ) j1 Lb
4 ez 0,
D
(
,
k
)
ku
Lb
0
u
u
0,
t
z
z
i ( ku ) j2 ikuj1 0,
E z
1 ku Lb , 2 ku Lb
i ez 4 j1 4 j2 0.
4 jb1 4 jb 2 0.
t
1
1
exp( i Lb t ) A2
exp( i Lb t ) exp ik ( z ut )
Ψ (t , z ) A1
i 4 Lb
i 4 Lb
2
2
u Lb A(t , z ) 0
z
t
2
Ψ(t , z ) J b1 , E z A(t , z ), 4 Lb
Lˆ A(t , z )
A(t , z ) f1 ( z ut ) exp( i Lb t ) f 2 ( z ut ) exp(i Lb t )
2
Lb
( , k ) 1
( ku ) 2
2
Lb
j ( , k ) j1 ( , k ) j2 ( , k ) i
ez ( , k )
4 ( ku ) 2
2
Lb
( ku ) | ez (k ) |2
Wl (k ) 1
3
( ku ) 16
E z2
WE
8
Wl
(1, 2 )
l
( k ) | e z ( k ) |2
(k )
Lb
8
m
m
2
WK n0b n~ u u~ n0b u 2
2
2
P m n0b n~ u u~ mn0b u mun~ mn0b u~ mn~u~
T
1
W WE WK dt
T 0
2
k e ( , k )
k
P 2 z
W
Lb
8

3.

2
jb1
jb1 Lb
u
E z 0,
t
z
4
jb 2
j
j
u b 2 u b1 0,
t
z
z
2
je Le
E z 0,
t 4
E z
4 jb1 4 jb 2 4 je 0.
t
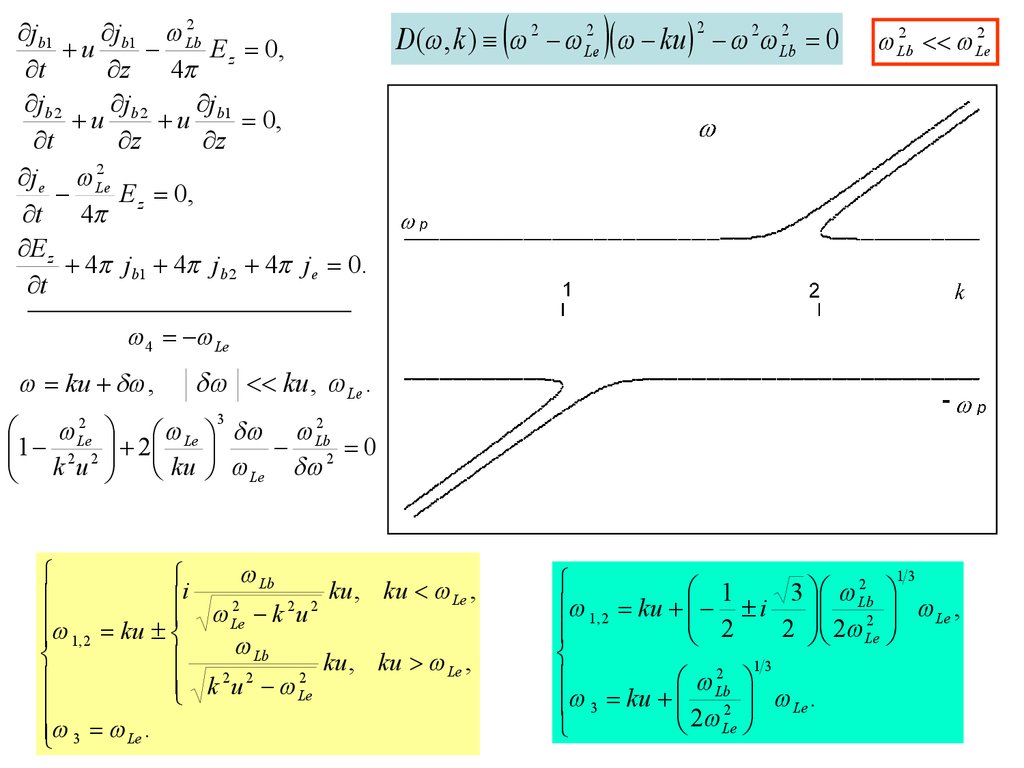
D( , k ) 2 Le2 ku 2 Lb2 0
2
2
2
Lb
Le
4 Le
ku ,
ku, Le .
3
2
2
Le Lb
Le
1 2 2 2
2 0
k
u
ku
Le
Lb
i
ku, ku Le ,
2
2 2
ku Le k u
1, 2
Lb
ku, ku Le ,
2
2
2
k u Le
3 Le .
13
2
1
3 Lb
2 Le ,
1, 2 ku i
2
2
2 Le
13
2
Lb
2 Le .
ku
3
2 Le

4.

jb1
j1
4
j
j
Ψ (t , z ) b 2 Am 2 exp i m (k )t ikz
j
j
e m 1
E
e
z
z ( m)
j1 , j2 , j , ez
(m)
m m ku
2
4
1
1 Le
1, ku m , m 2 m , i 2 m
Lb
Lb
ch(| | t ), ku Le ,
jb1 (t , z ) j10 exp ik ( z ut )
cos(| | t ), ku Le .
jb 2 (t , z ) j10
3
1
jb1 (t , z ) j10 exp ik ( z ut ) exp i m 0t ,
3
m 1
3
ku Le , j (t , z ) 1 j ku exp ik ( z ut ) exp i t .
b2
10
m
m 0
3
0
m 1
sh(| | t ),
ku
exp ik ( z ut )
sin(| | t ), ku Le .
Lb
i
ku
2
2 2
Le k u
13
2
Lb
0 2 Le
2 Le
2
2
2
2
2
2 Le u Lb 2 A(t , z ) 0
z
t
t
t
1
1 i 3
1 i 3
, 2
, 3 1.
2
2
Ψ (t , z ) jb1 , jb 2 , je , E z
A
2 ˆ
2
2
2
2
ˆ
ˆ
Lb
LA, Lb
u
, Le
L
Adt
,
4
L
A .
z

5.

D( , k ) ( 2 Li2 )( ku ) 2 2 Le2 0
Li2
Le2
( , k ) 1 2
( ku ) 2
l
1
3
1, 2 i
2 2
2
2
Li
2
Le
13
Li2
3 2 Le .
2 Le
2
2
Le
Lb
( , k ) 1 2
( ku ) 2
l
13
Le ,
1, 2
ku
i
, ku Le ,
Li
2
2 2
Le k u
ku
Li
, ku Le .
2 2
2
k u Le