Похожие презентации:
Неинерциальные системы отсчета. Колебания и волны
1. Лекция 5-6
Неинерциальные системы отсчетаКолебания и волны
2. Неинерциальные системы отсчёта. Силы инерции
Для ИСО: a = aотнКак «подправить» уравнение динамики в НСО? maотн = F +
Fин
Для НСО: a = aотн + a*
ma = maотн + ma*
maотн = ma + (-ma*) = F + Fин
Fин = -ma*
Сила инерции Fин = -ma* зависит от:
1.
2.
параметров НСО
положения и скорости частицы
3. Поступательная сила инерции
F = - ma0В ускоряющейся ракете на все тела действует сила инерции F =
- ma0 - возникает однородное силовое поле, эквивалентное
однородному полю тяжести.
Принцип эквивалентности:
Никакими физическими опытами невозможно отличить
однородное поле тяготения от однородного поля сил
инерции.
Состояние невесомости при свободном падении в однородном
поле тяжести эквивалентно движению в свободном
пространстве: силу тяжести компенсирует сила инерции.
4. Поступательная сила инерции Fпси = - ma0.
Вес тела в лифте;Невесомость – проявление силы инерции: сила тяжести
уравновешивается силой инерции!
0 N maин mg
5. Основное уравнение динамики в неинерциальной системе отсчёта*
Если система перемещается поступательно с ускорением a0 ивращается с постоянной угловой скоростью ω, то:
ma′ = F – ma0 + mω2r + 2m[v′ ω]
F – реальная сила
Fпси = m (- a0) – поступательная сила инерции
Fцб = mω2r – центробежная сила инерции
Fкор = 2m[vотнω] – сила Кориолиса.
Сила Кориолиса перпендикулярна скорости не производит
работы!
6. Особенности сил инерции
Силы инерции существуют только в НСОСилы инерции обусловлены не взаимодействием тел, а
свойствами НСО. Третий закон Ньютона для сил инерции
не работает.
Все силы инерции пропорциональны массе тела (подобно
силам тяготения)
7. Неинерциальность систем отсчета
Ускорения из-за вращенияземли вокруг оси
an Rземля сут 2 ~ 0.032 m / c 2
2
2
7.3*10 5 с 1
T
24*3600
Rземля 6500км
Ускорения из-за вращения земли
вокруг солнца
an Rорб год 2
сут
Rорб 150 млн.км
Ускорения из вращения нашей
галактики
0.000001 m / c 2
~ 0.0055 m / c 2
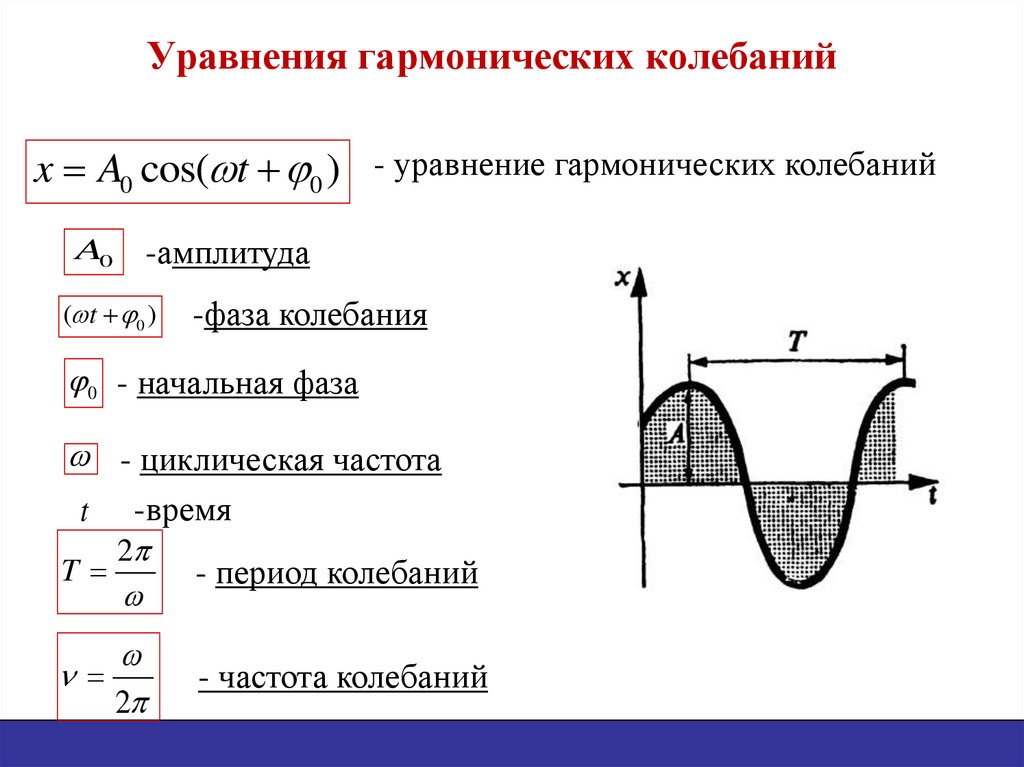
8. Уравнения гармонических колебаний
x A0 cos( t 0 ) - уравнение гармонических колебанийA0
-амплитуда
( t 0 )
-фаза колебания
0 - начальная фаза
- циклическая частота
t -время
2
T
- период колебаний
2
- частота колебаний
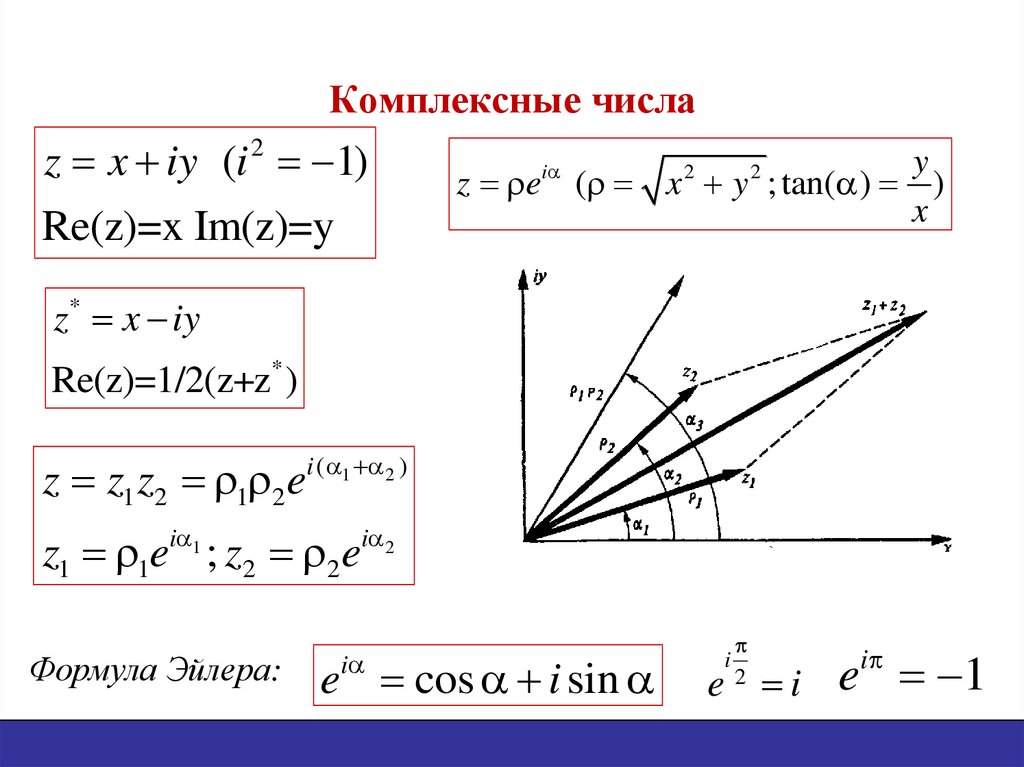
9. Комплексные числа
z x iy (i 2 1)Re(z)=x Im(z)=y
y
z e ( x y ; tan( ) )
x
i
2
2
z* x iy
Re(z)=1/2(z+z* )
z z1 z2 1 2 ei ( 1 2 )
z1 1ei 1 ; z2 2ei 2
Формула Эйлера:
i
e cos i sin
i
2
e i
i
e 1
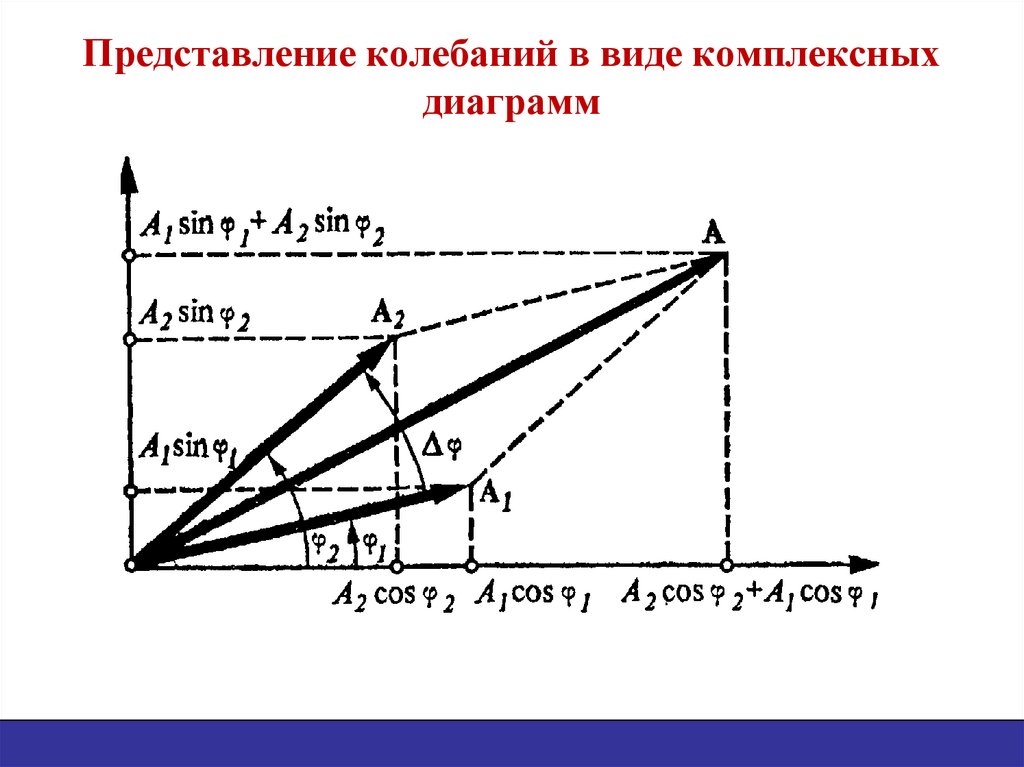
10. Представление колебаний в виде комплексных диаграмм
11. Пружинный маятник
ma Mg N Fупрmx kx
x x 0
2
Решение ищем в виде:
e t ( 2 2 ) 0
k
m
x e
t
x 2 e t
i Общее решение: x C1e i C2e i
Условие действительности х: C1 C2*
Решение:
A0 i 0
e
2
A0 i ( t 0 ) A0 i ( t 0 )
x
e
e
A0 cos( t 0 )
2
2
12. Пружинный маятник
ma Mg N Fупрmx kx
x x 0
2
Решение ищем в виде:
e t ( 2 2 ) 0
k
m
x e
t
x 2 e t
i Общее решение: x C1e i C2e i
Условие действительности х: C1 C2*
Решение:
A0 i 0
e
2
A0 i ( t 0 ) A0 i ( t 0 )
x
e
e
A0 cos( t 0 )
2
2
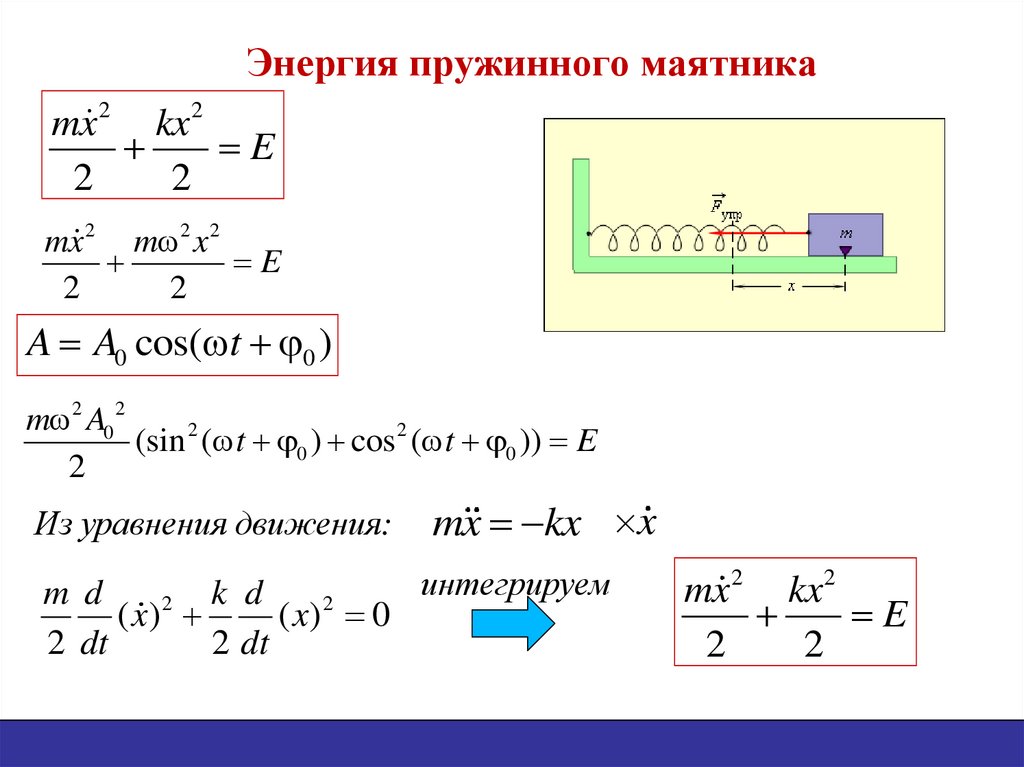
13. Энергия пружинного маятника
mx 2 kx 2E
2
2
mx 2 m 2 x 2
E
2
2
A A0 cos( t 0 )
m 2 A0 2
(sin 2 ( t 0 ) cos 2 ( t 0 )) E
2
Из уравнения движения:
m d
k d
( x) 2
( x) 2 0
2 dt
2 dt
mx kx x
интегрируем
mx 2 kx 2
E
2
2
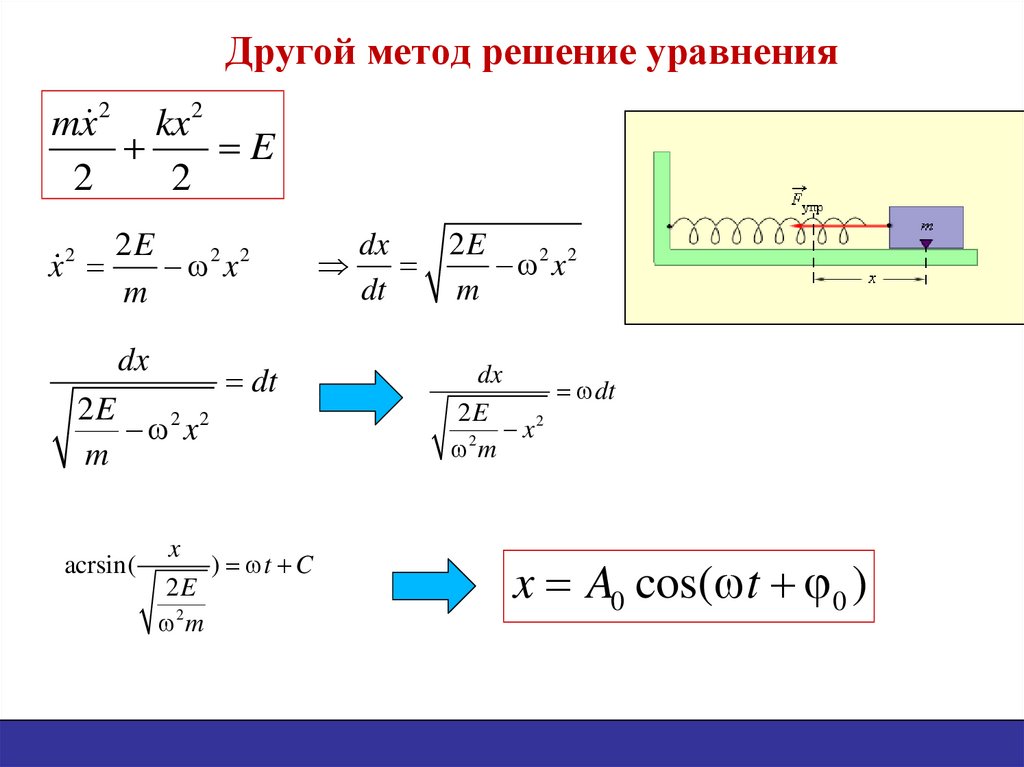
14. Другой метод решение уравнения
mx 2 kx 2E
2
2
2E
x
2 x 2
m
2
dx
2E
2 x 2
m
acrsin(
dt
x
) t C
2E
2 m
dx
2E
2 x 2
dt
m
dx
dt
2E
2
x
2 m
x A0 cos( t 0 )
15. Математический маятник
ma mg NИз закона сохранения
энергии:
d
dt
ml 2 2
(1 cos( ))mlg E
2
ml 2 sin( )mlg 0
sin( ) 2 0
1
0,
2
g
l
0 cos( t 0 )
16. Изохронный маятник
sin( ) 2 0javascript:void();
17. Физический маятник
Физический маятник — это твердое тело,совершающее под действием силы тяжести
колебания вокруг неподвижной горизонтальной оси
Действующие силы:
mg , N
Уравнение динамики вращательного движения
относительно оси подвеса O :
J J M mg sin( )mgd
(1)
J
- Момент инерции относительно оси O
d
- Расстояние между осью O и центром масс С
1
2 0,
gmd
J
0 cos( t 0 )
18. Приведенная длина физического маятника
0,2
J
L
md
gmd
J
-Приведенная длина
Если перевесить маятник в точку O’, то
частота колебаний не измениться:
По теореме Штейнера:
J c md 2
Jc
L
d
md
md
J C ( L d )2 m
L
m( L d )
L d
JC
L
md
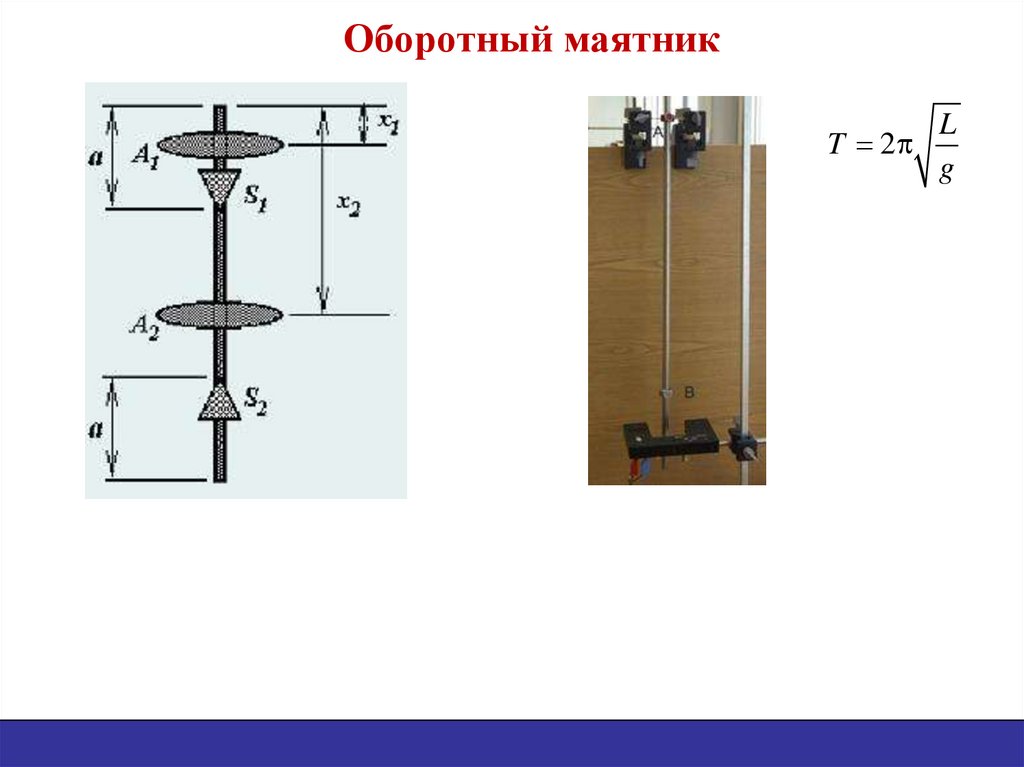
19. Оборотный маятник
LT 2
g
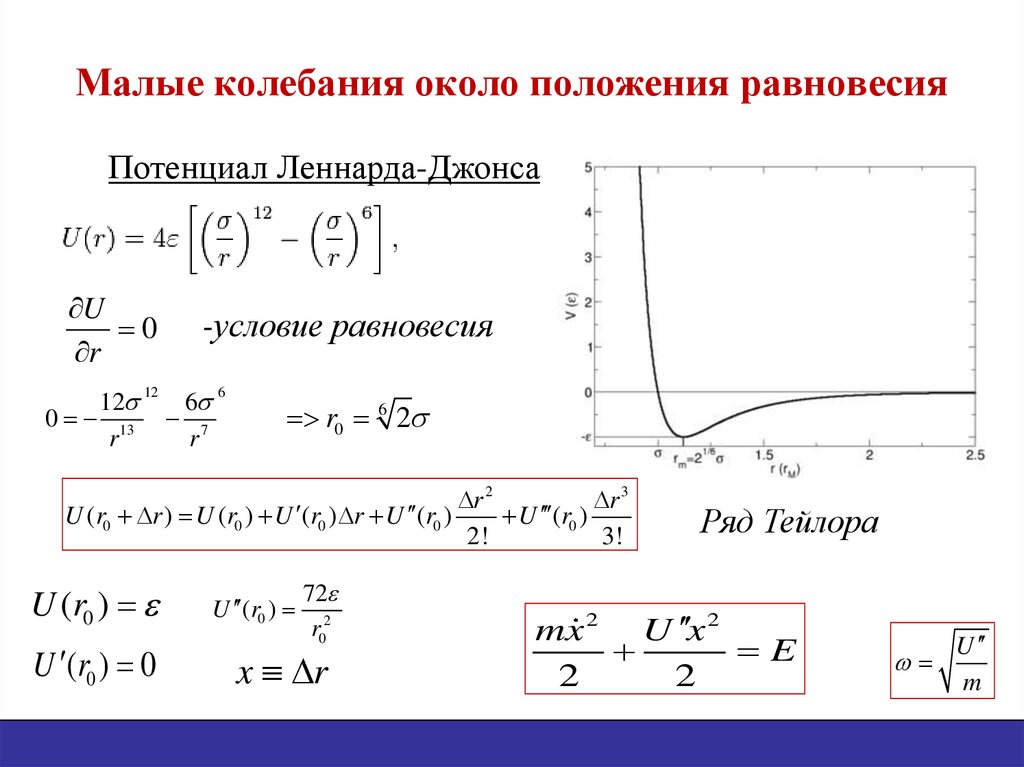
20. Малые колебания около положения равновесия
Потенциал Леннарда-ДжонсаU
0
r
12
0 13
r
12
-условие равновесия
6
7
r
6
r0 6 2
r 2
r 3
U (r0 r ) U (r0 ) U (r0 ) r U (r0 )
U (r0 )
2!
3!
U (r0 )
U (r0 ) 0
U (r0 )
72
r02
x r
Ряд Тейлора
mx 2 U x 2
E
2
2
U
m
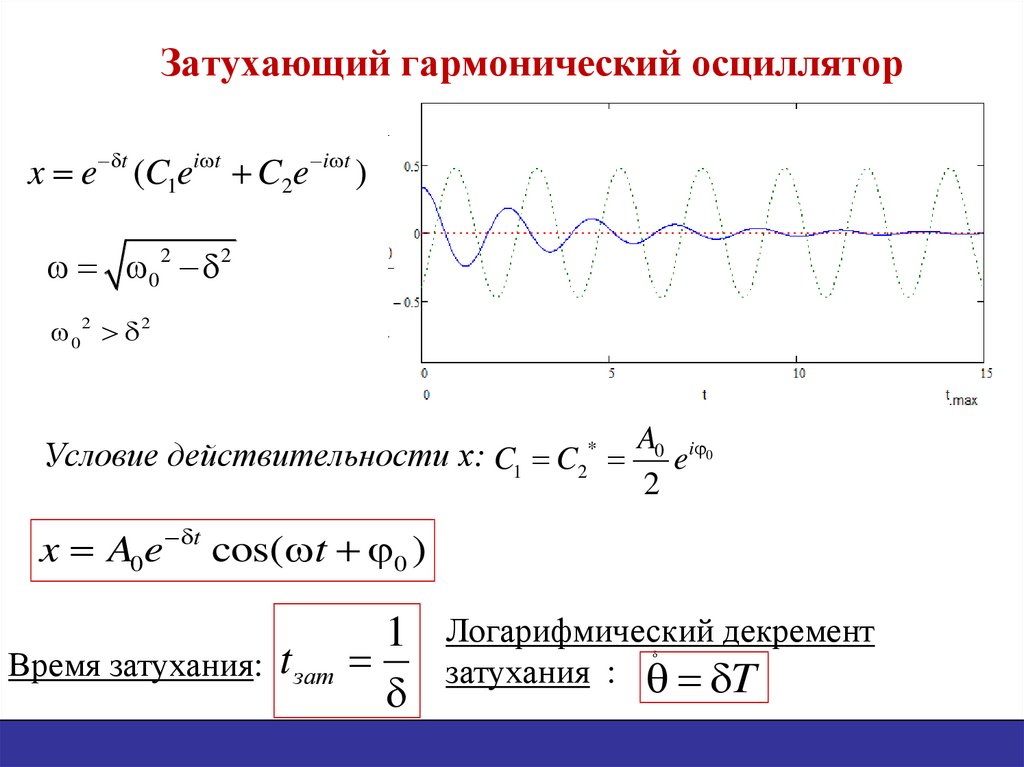
21. Затухающий гармонический осциллятор
ma Fупр Fcопрmx kx cx
Уравнения затухающих колебаний:
x 2 x 0 x 0
2
k
c
,
m
2m
0
Решение ищем в виде:
x e
e t ( 2 2 0 2 ) 0
Общее решение:
t
x e
t
1,2 i 02 2
x C1e 1t C2e 2t
x e t (C1ei t C2e i t )
02 2
x 2 e t
22. Затухающий гармонический осциллятор
x e t (C1ei t C2e i t )02 2
0 2 2
Условие действительности х: C1 C2*
A0 i 0
e
2
x A0 e t cos( t 0 )
Время затухания:
t зат
1
Логарифмический декремент
затухания : T
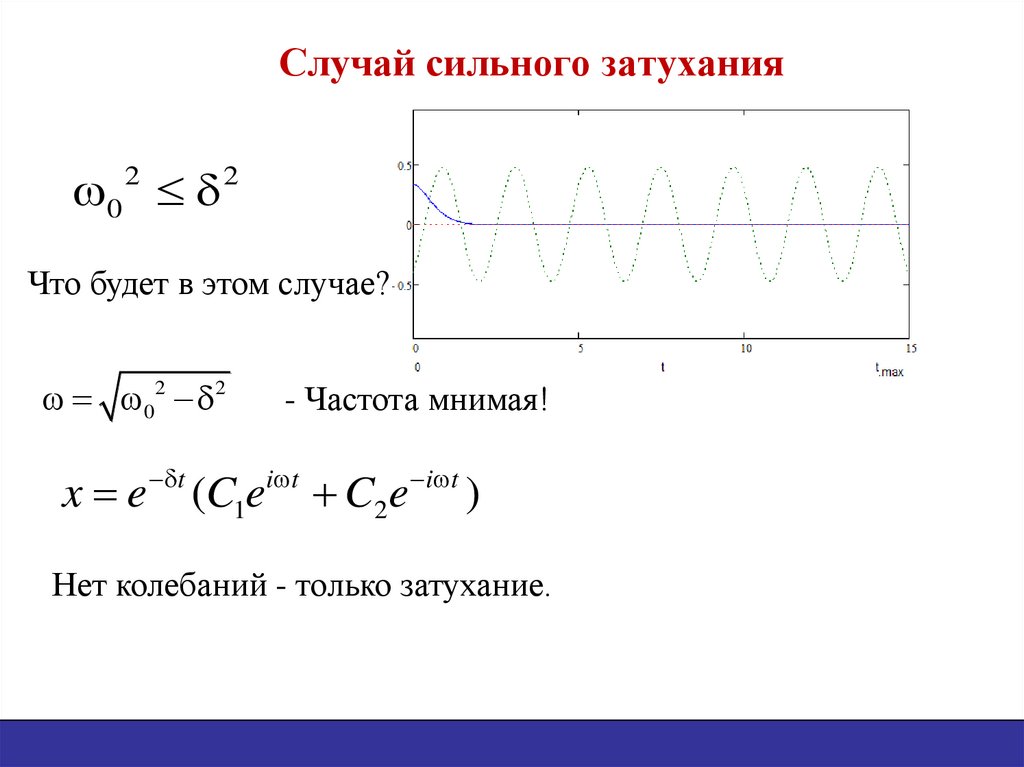
23. Случай сильного затухания
02
2
Что будет в этом случае?
02 2
t
x e (C1e
- Частота мнимая!
i t
C2 e
i t
)
Нет колебаний - только затухание.
24. Масштабирование физического маятника
Что будет, если увеличить маятник в α раз?0
gmd
J
c
2m
2
1 2
0
0
m
3
J
5
d
c
0
1
2
~ 2
2 3
1 2 3
1 2 1
2
0
0
2 0
25. Вынужденные колебания
ma Fупр Fcопр F (t )F0
x 2 x 0 x exp(i t )
m
Общее решение = общее решение однородного
k
c
0
,
m
2m
уравнения + частное решение неоднородного
2
t / 1
Ae
Решение ищем в виде: x
i t
x i Ae
F0
exp(i t ) A( i 2 0 ) exp(i t )
m
2
2
i t
x 2 Aei t
26. Вынужденные колебания
F0A( 0 i 2 )
m
2
2
F0
A (( 0 ) 4 )
m
2
2 2
2
2
A A0 ei
F0
A0
m
1
(( 0 2 2 )2 4 2 2 )
2
tan 2 2
0
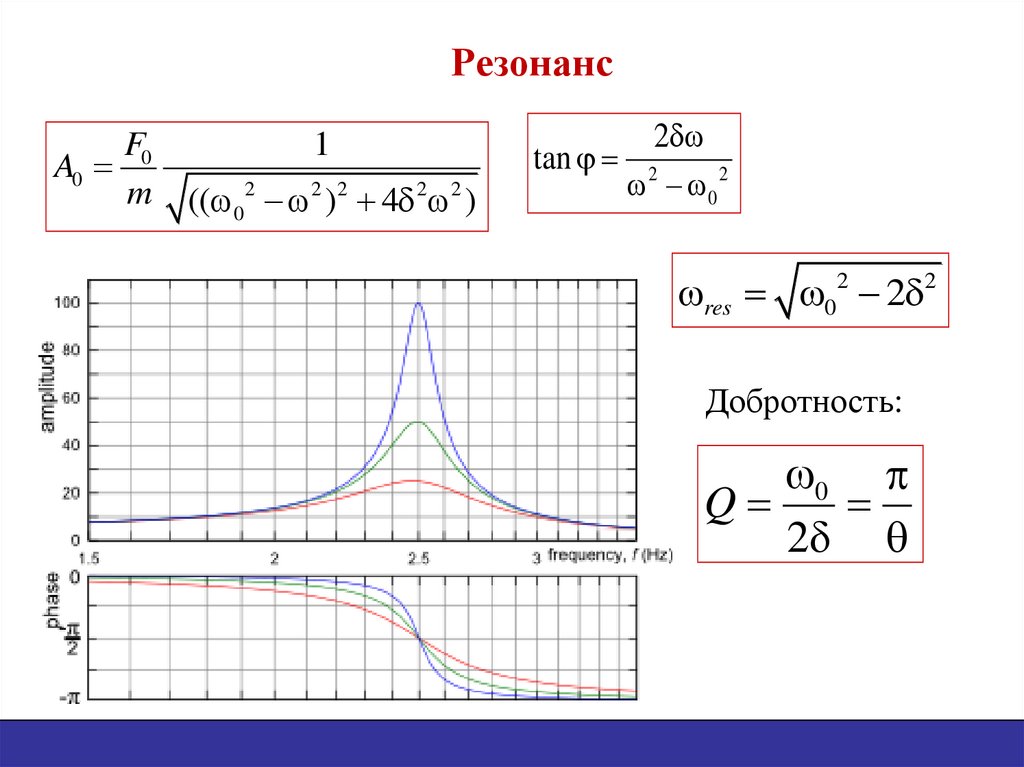
27. Резонанс
F0A0
m
1
(( 0 2 2 )2 4 2 2 )
tan
2
2 0 2
res 02 2 2
Добротность:
0
Q
2
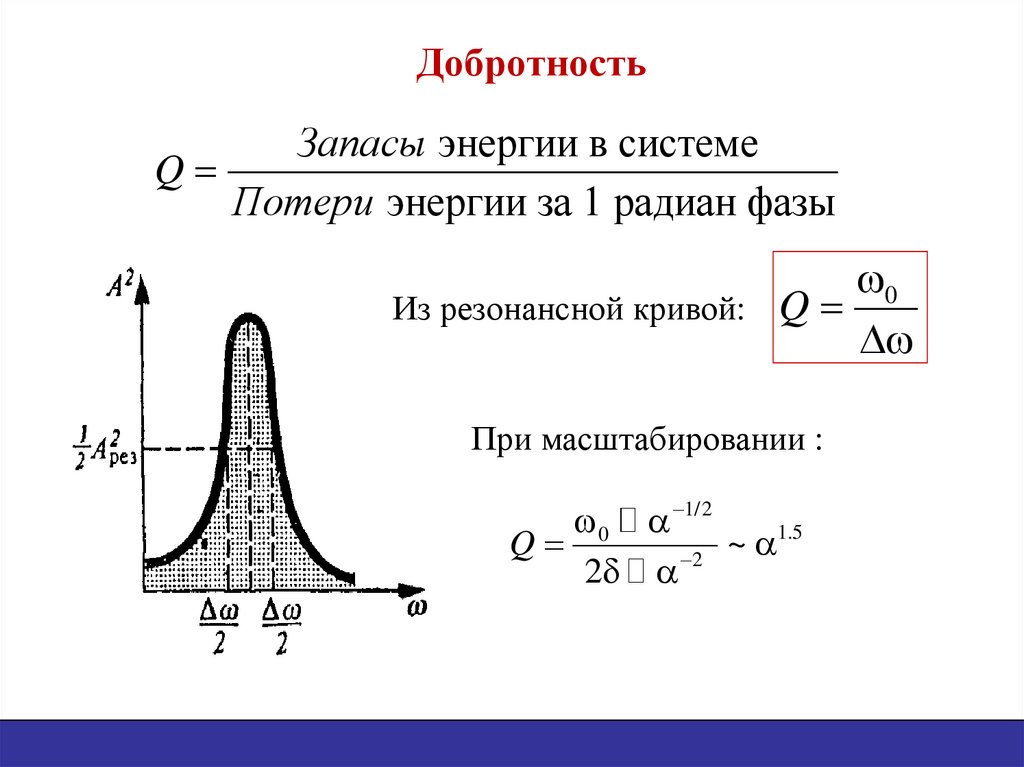
28. Добротность
Запасы энергии в системеQ
Потери энергии за 1 радиан фазы
0
Из резонансной кривой: Q
При масштабировании :
0 1/2
1.5
Q
~
2 2
29. Резонанс и аварии
30. Сложение колебаний одинаковой частоты
A1 exp(i t 1 ) A2 exp(i t 2 )A exp(i t ) A1 exp(i t 1 ) A2 exp(i t 2 )
A2 A12 A2 2 2 A1 A2 cos( 1 2 )
Из теоремы косинусов
31. Сложение колебаний разной частоты. Биения
A exp(i 1t ) A exp(i 2t )A exp(i
( 1 2 )
( 2 )
( 1 )
t )(exp(i 1
t ) exp(i 2
t ))
2
2
2
2 A exp(i
( 1 2 )
( 2 )
t ) cos( 1
t)
2
2
1 2 1
2 A exp(i t ) cos(
t)
2
32. Волны
Волна распространение колебаний в пространствеВолновая поверхность - геометрическое место точек с одинаковой фазой.
Фронт волны - геометрическое место точек, до которых распространилась волна
в фиксированный момент времени.
Луч - линия перпендикулярная фронту и совпадающая с направлением скорости
распространения.
(Обычно луч проводят от источника до точки наблюдения)
33. Продольные волны
Продольная волна – это волна, в которойколебания происходят вдоль направления
распространения волны.
Механические продольные волны могут
распространяться в газах, жидкостях и твердых
телах.
.
34. Поперечные волны
Поперечная волна – это волна, в которойколебания происходят перпендикулярно
направлению распространения волны.
Механические поперечные волны могут
распространяться в твердых телах и на границе
двух сред.
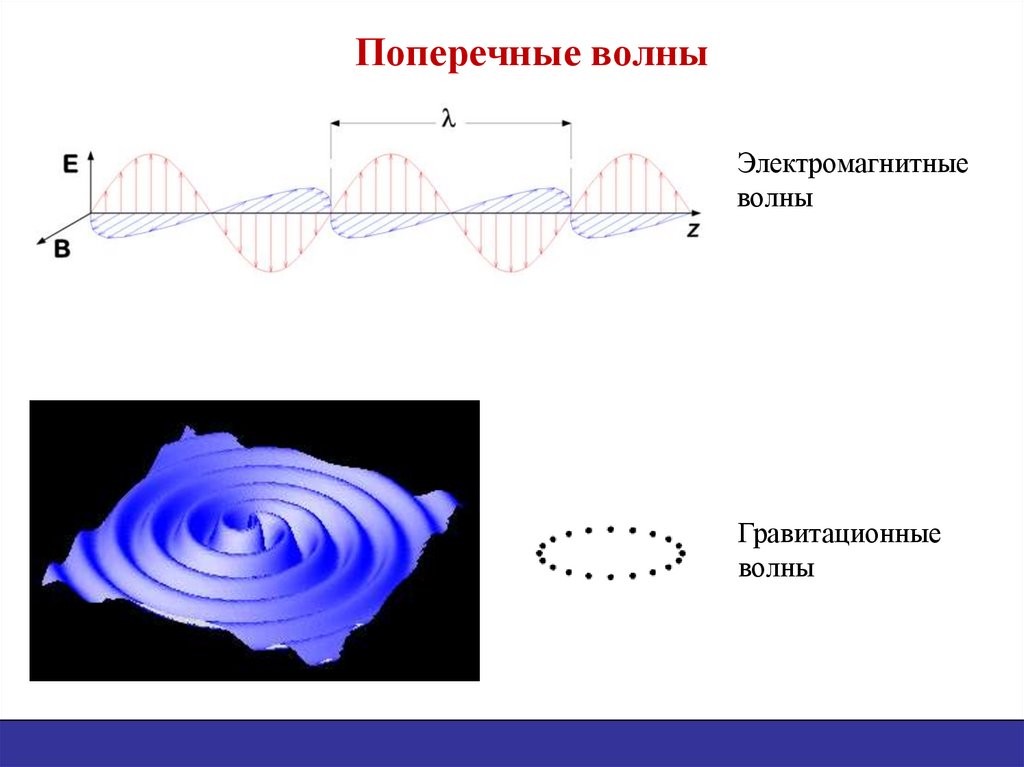
35. Поперечные волны
Электромагнитныеволны
Гравитационные
волны
36. Волновое уравнение для системы пружинок
(Рассмотрим бесконечную цепь – одинаковые пружинкижесткостью- k, одинаковые массы – m, на расстоянии - а друг от
друга, x – смешение относительно положения равновесия )
mxi 2kxi kxi 1 kxi 1
m i 2k i k i 1 k i 1
a 2k
i
(( i 1 i ) ( i i 1 ))
2
ma
i
a k ( i 1 i ) ( i i 1 )
(
)
ma
a
a
2
Уравнение движения mассы - i
Уравнение движения mассы – i в другом виде
Еще раз перепишем, где а – расстояние между
массами m
a 2 k i 1/2 i 1/2
i
(
)
ma
x
x
37.
a 2 k ( i 1 i ) ( i i 1 )i
(
)
ma
a
a
i 1/2
x
i 1/2
x
i 1/2 i 1/2
)
a k
x )
i
( x
m
a
2
Таким образом мы заменили разность
производными один раз.
a 2 k i 1/2 i 1/2
i
(
)
ma
x
x
(
И аналогично, заменяя разность
производной еще раз:
a 2 k 2 i
i
( 2)
m x
Выводы:
A)Это волновое уравнение.
B)Его получение математически корректно, когда разность смешений мало отличается от
производной, т.е. в гладком случае достаточно длинных волн.
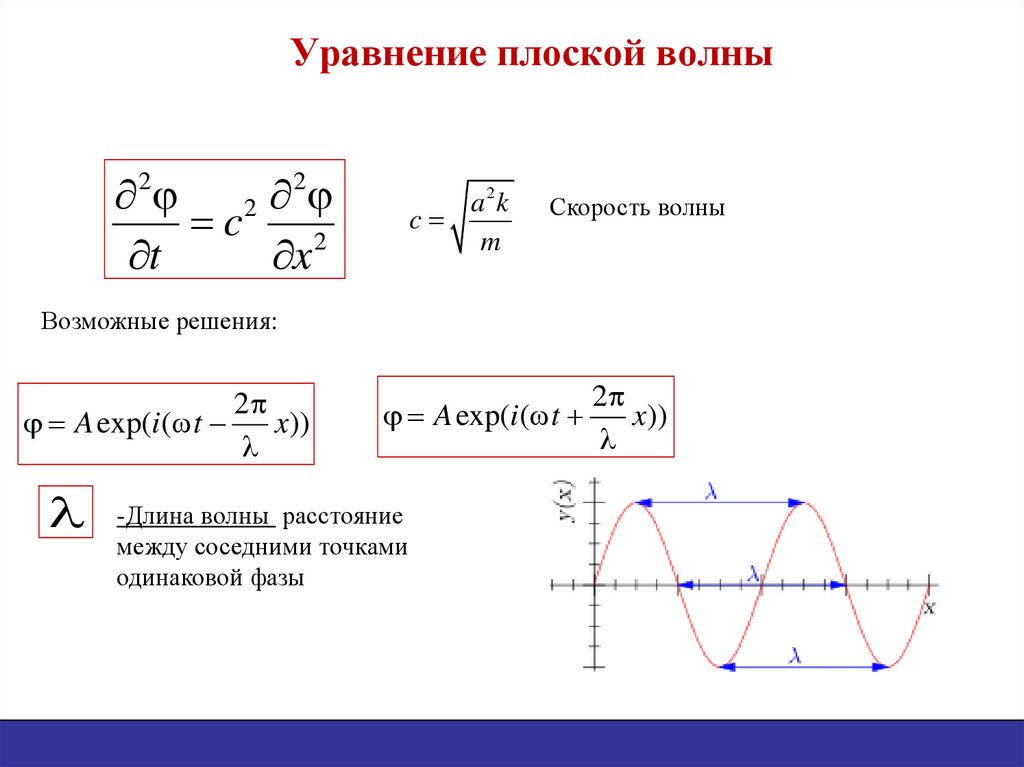
38. Уравнение плоской волны
22
2
c
t
x 2
a2k
c
m
Скорость волны
Возможные решения:
2
A exp(i ( t
x))
A exp(i ( t
-Длина волны расстояние
между соседними точками
одинаковой фазы
2
x))
39. Уравнение бегущей волны
A exp(i ( t kx))( t kx)
v
k
k
2
Волновое число
Фаза волны
Фазовая скорость - скорость распространения
определенной фазы колебаний.
40. Стоячие волны
A exp(i ( t kx)) A exp(i ( t kx))A exp(i ( t kx)) A exp(i ( t kx)) A exp(i t )(exp( ikx) exp(ikx))
Уравнение стоячей волны
2
2 A exp(i t ) cos( x)
2 A exp(i t ) cos(kx)
Пучности:
Узлы:
2
x m
2
1
x ( m )
2




























 Физика
Физика