Похожие презентации:
Готовимся к ЕГЭ. Прототипы по теме «Пирамида»
1. Готовимся к ЕГЭ. Прототипы по теме «Пирамида».
2.
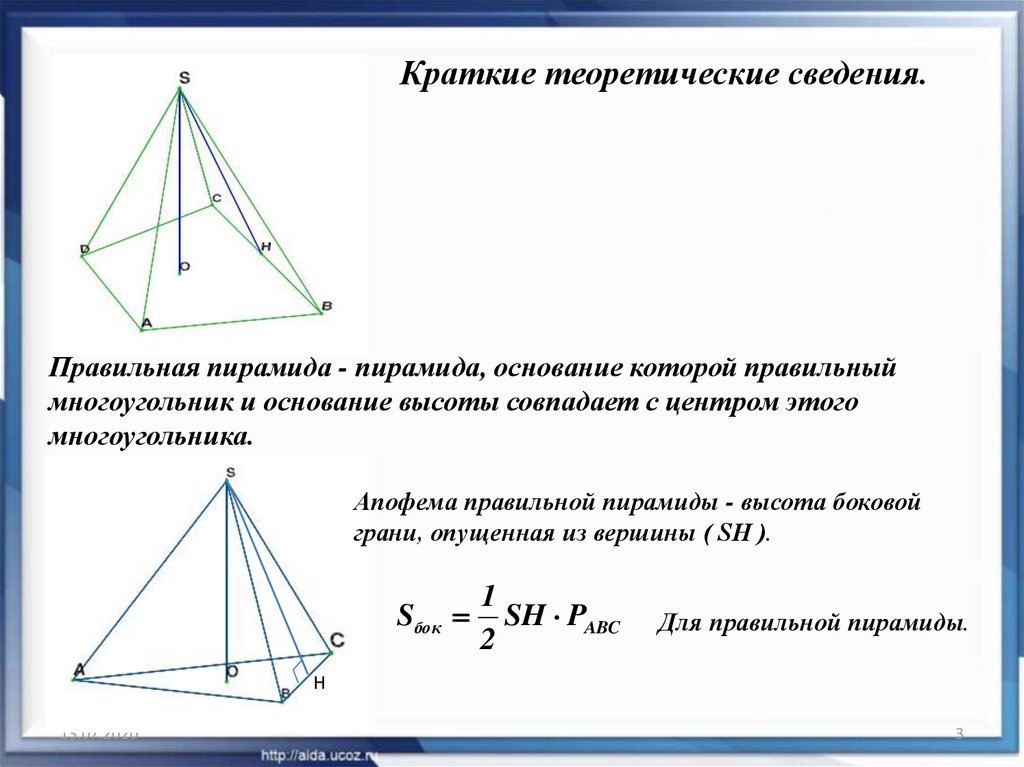
Краткие теоретические сведения.Пирамидой называется многогранник, основанием которой является
многоугольник, а боковые грани - треугольники, имеющие общую
точку. Общая точка является вершиной пирамиды.
Отрезки, соединяющие вершину пирамиды с вершинами основания
называются боковыми ребрами.
Высотой пирамиды является перепендикуляр, опущенный из вершины
на плоскость основания ( SO ).
13.07.2020
2
3.
Краткие теоретические сведения.Правильная пирамида - пирамида, основание которой правильный
многоугольник и основание высоты совпадает с центром этого
многоугольника.
Апофема правильной пирамиды - высота боковой
грани, опущенная из вершины ( SH ).
Sбок
1
SH PABC
2
Для правильной пирамиды.
H
13.07.2020
3
4. В правильной треугольной пирамиде SABC R — середина ребра BC, S — вершина. Известно, что AB=1, а SR=2. Найдите площадь боковой
В правильной треугольной пирамиде SABC R — серединаребра BC, S — вершина. Известно, что AB=1, а SR=2.
Найдите площадь боковой поверхности.
№3
Пирамида правильная. SR-апофема.
O
R
Sбок
1
PABC SR
2
Sбок
1
1 3 2 3
2
Ответ:
13.07.2020
3
Авдеев Саша 10В
4
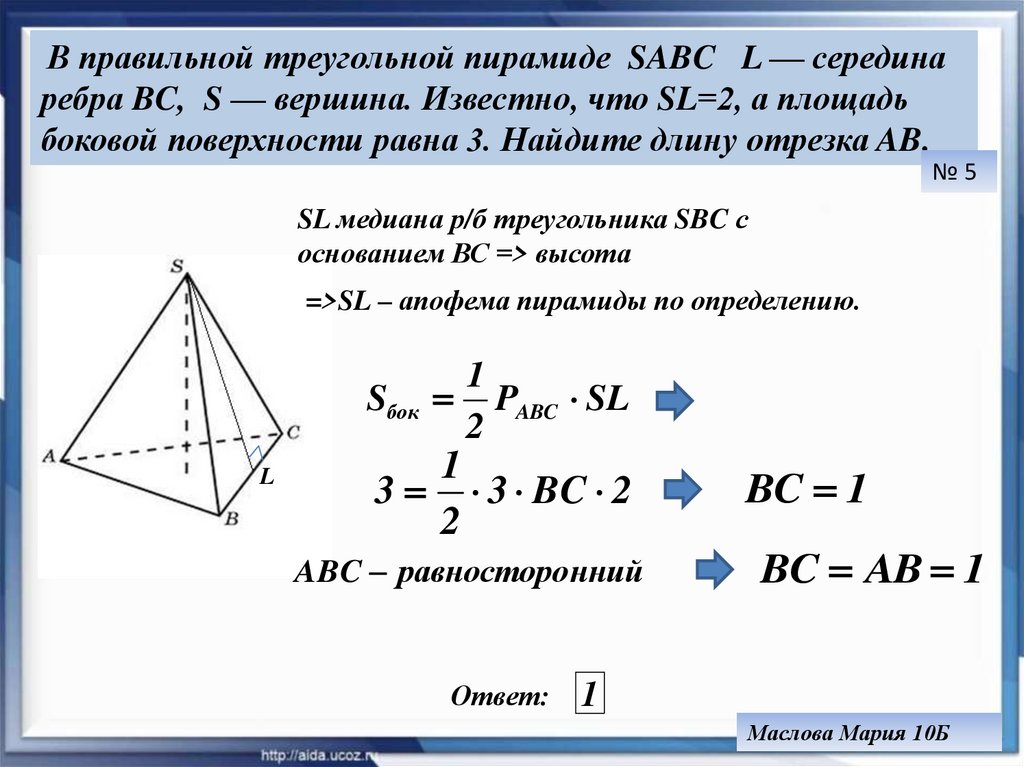
5.
В правильной треугольной пирамиде SABC L — серединаребра BC, S — вершина. Известно, что SL=2, а площадь
боковой поверхности равна 3. Найдите длину отрезка AB.
№5
SL медиана р/б треугольника SBC с
основанием ВС => высота
=>SL – апофема пирамиды по определению.
Sбок
L
1
PABC SL
2
1
3 3 BC 2
2
ABC равносторо нний
Ответ:
BC 1
BC AB 1
1
Маслова Мария 10Б
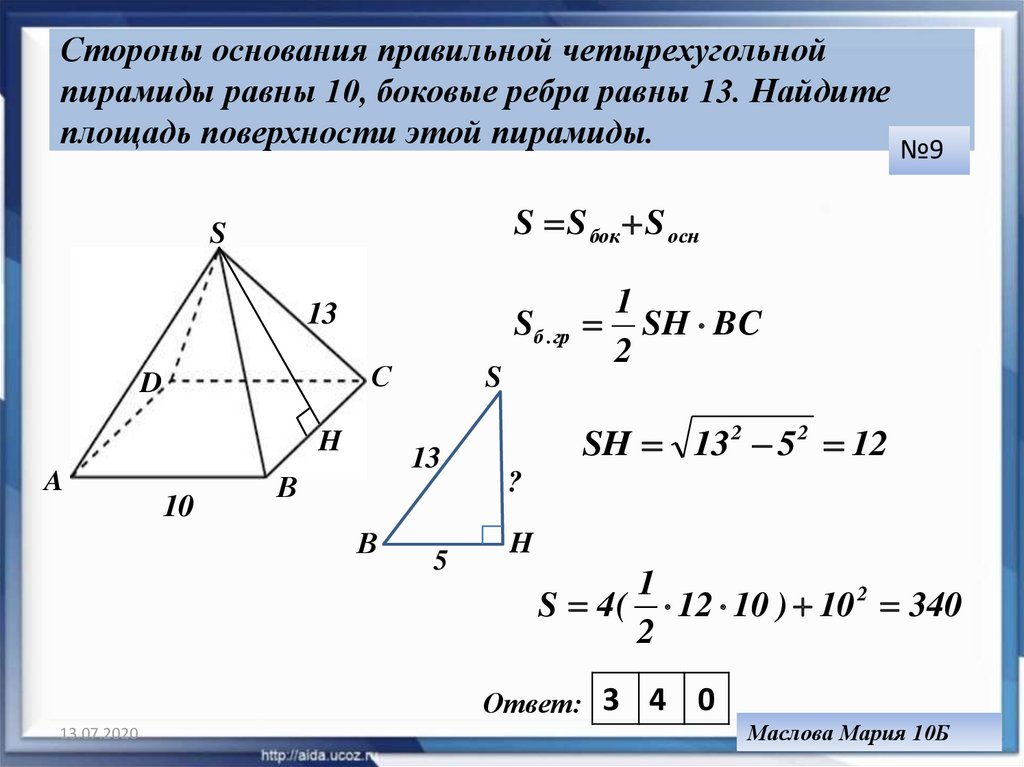
6. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой
пирамиды.№9
S S бок S осн
S
Sб .гр
13
С
D
H
A
10
S
13
В
В
5
1
SH BC
2
SH 132 5 2 12
?
H
1
S 4 ( 12 10 ) 10 2 340
2
Ответ: 3
13.07.2020
4 0
Маслова Мария 10Б
7.
Найдите площадь боковой поверхности правильнойчетырехугольной пирамиды, сторона основания которой
равна 6 и высота равна 4.
№ 25
S
Найдем апофему пирамиды SH:
S
4
D
С
O
А
6
H
В
4
O
Sбок
Треугольник – египетский:
SH=5
3
H
1
1
PABCD SH 6 4 5 60
2
2
Ответ: 6 0
Счастьева Анастасия 10А
8.
Во сколько раз увеличится площадь поверхности пирамиды,если все ее ребра увеличить в 2 раза?
№26
Запомни: при увеличении
всех линейных элементов
фигуры
в k раз ее площадь
увеличивается в k2 раз.
В нашей задаче ребра увеличились в два раза, значит
площадь увеличилась в четыре раза.
Ответ: 4
Чунин Павел 10А
9.
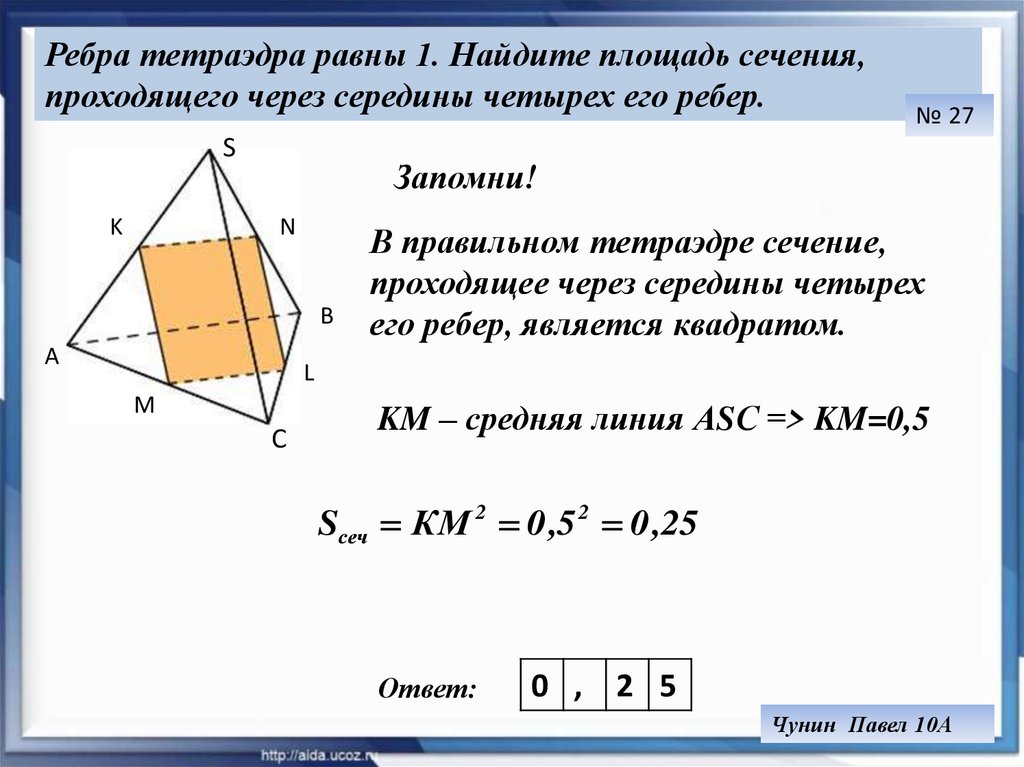
Ребра тетраэдра равны 1. Найдите площадь сечения,проходящего через середины четырех его ребер.
S
K
№ 27
Запомни!
N
B
A
В правильном тетраэдре сечение,
проходящее через середины четырех
его ребер, является квадратом.
L
M
C
KM – средняя линия АSС => KM=0,5
Sсеч КМ 2 0 ,5 2 0 ,25
Ответ:
0 , 2 5
Чунин Павел 10А






 Математика
Математика








