Определенный интеграл

1. Определенный интеграл

Математический анализ

2. Формула Ньютона-Лейбница

a
b
b
f ( x) F ( x) F (b) F (a)
a
Определённый интеграл равен
разности
значений первообразной при
верхнем и нижнем пределах
интегрирования.

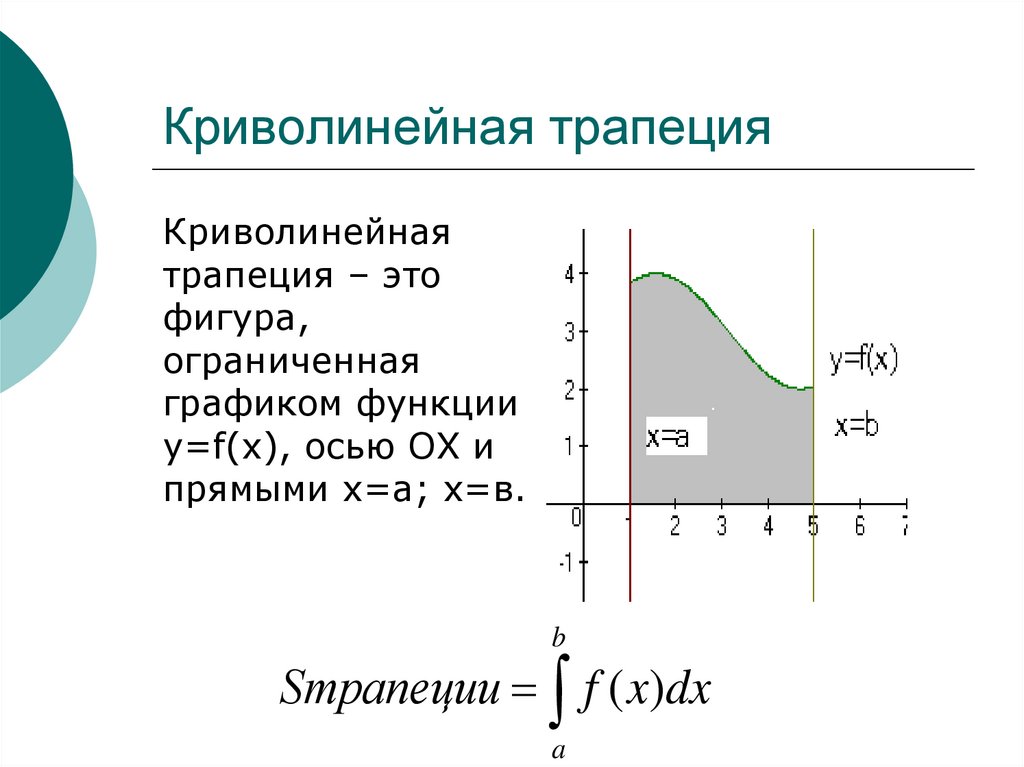
3. Криволинейная трапеция

Криволинейная
трапеция – это
фигура,
ограниченная
графиком функции
y=f(x), осью ОХ и
прямыми х=а; х=в.
b
Sтрапеции f ( x)dx
a

4.

y=f(x)
x=a
x=b
b
a
y=0
b
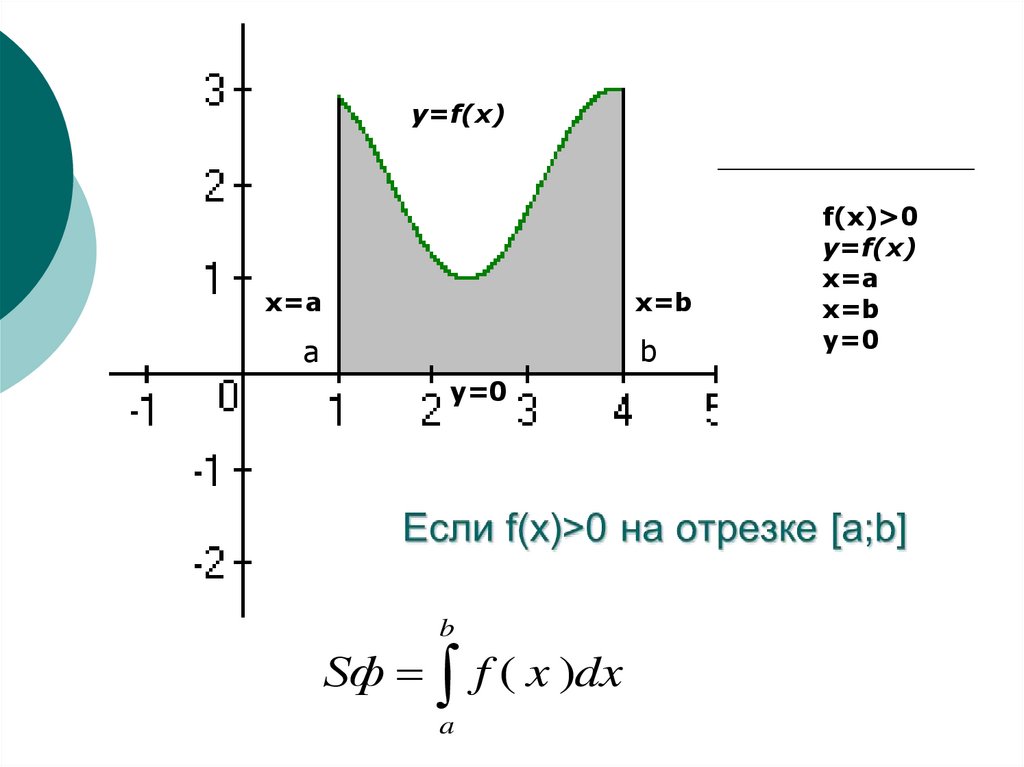
Sф f ( x )dx
a
f(x)>0
y=f(x)
x=a
x=b
y=0

5.

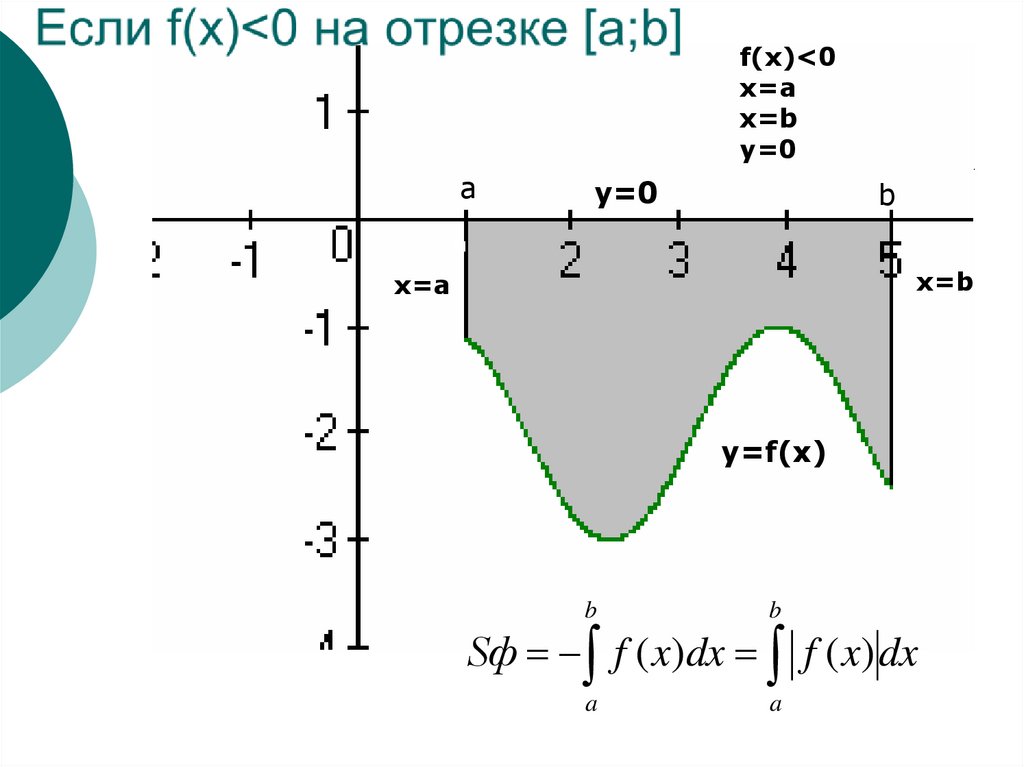
f(x)<0
x=a
x=b
y=0
a
y=0
b
x=b
x=a
y=f(x)
b
b
a
a
Sф f ( x)dx f ( x) dx

6.

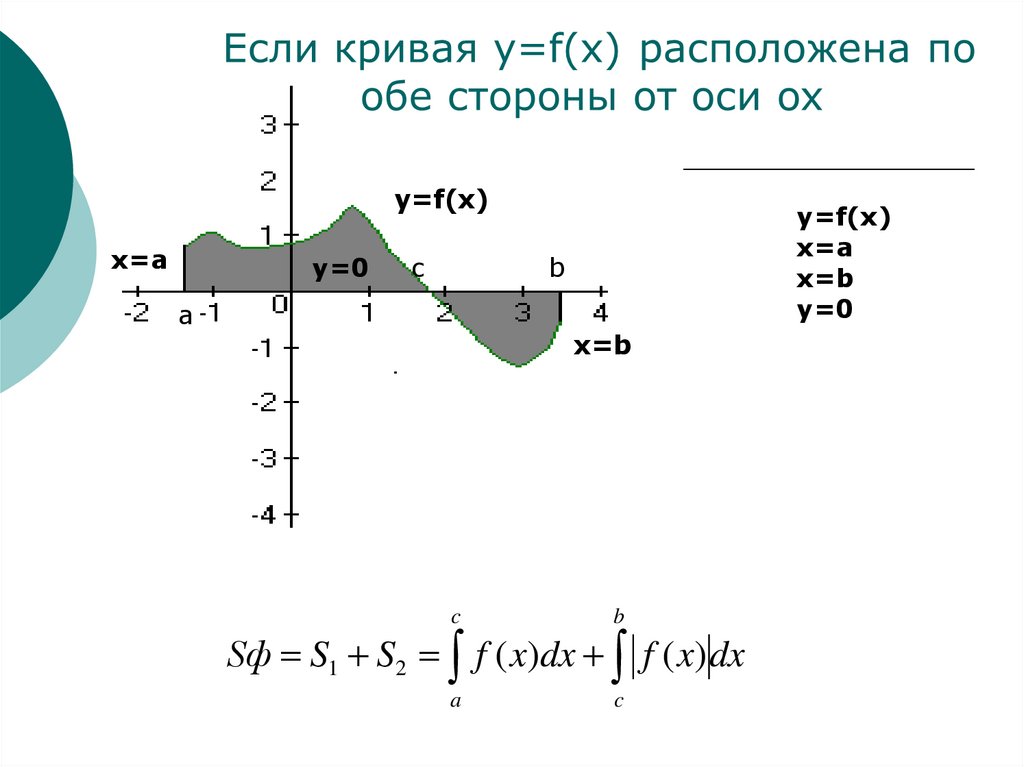
y=f(x)
x=a
y=0
y=f(x)
x=a
x=b
y=0
b
c
a
x=b
c
b
a
c
Sф S1 S2 f ( x)dx f ( x) dx

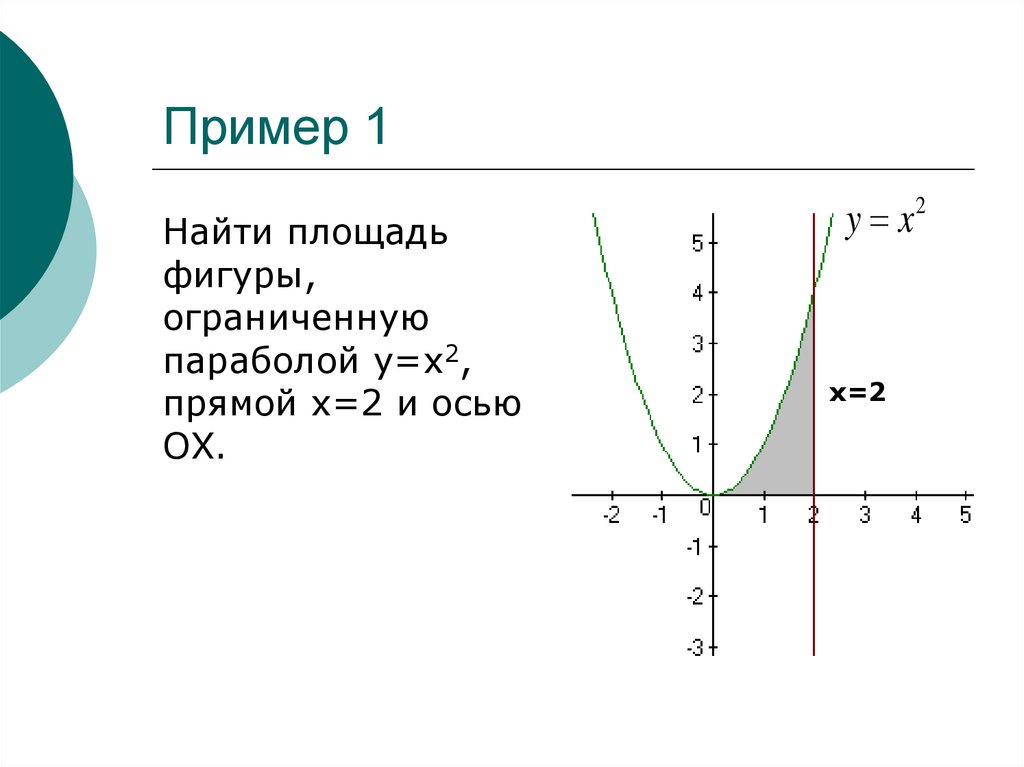
7. Пример 1

Найти площадь
фигуры,
ограниченную
параболой у=х2,
прямой х=2 и осью
ОХ.
y x2
x=2

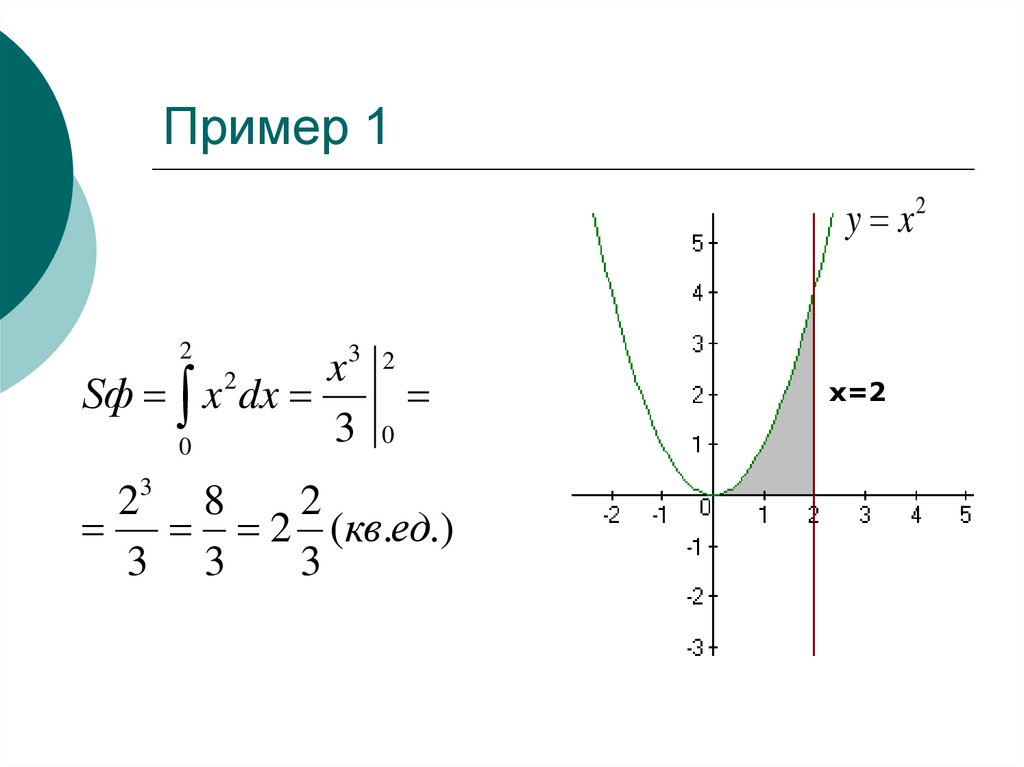
8. Пример 1

y x2
2
3
x
Sф x 2 dx
3
0
2
0
23 8
2
2 (кв.ед.)
3 3
3
x=2

9. Коротко об интеграле можно сказать так : ИНТЕГРАЛ – ЭТО ПЛОЩАДЬ криволинейной трапеции

10. Архимед (ок. 287-212 до н.э.)

Греческий физик и
математик.
Ему принадлежит метод
нахождения длин и
площадей, предвосхитивший
интегральное исчисление

11. Исаак Ньютон (1643 - 1727)

Английский физик и математик.
“Когда величина является
максимальной или
минимальной, в этот момент
она не течет ни вперед, ни
назад.”
И.Ньютон

12. Готфрид Вильгельм Лейбниц (1646 - 1716)

Немецкий математик, физик,
философ
“Предупреждаю, чтобы
остерегались отбрасывать dx,ошибка , которую часто
допускают и которая
препятствует продвижению
вперед.”
Г.В.Лейбниц

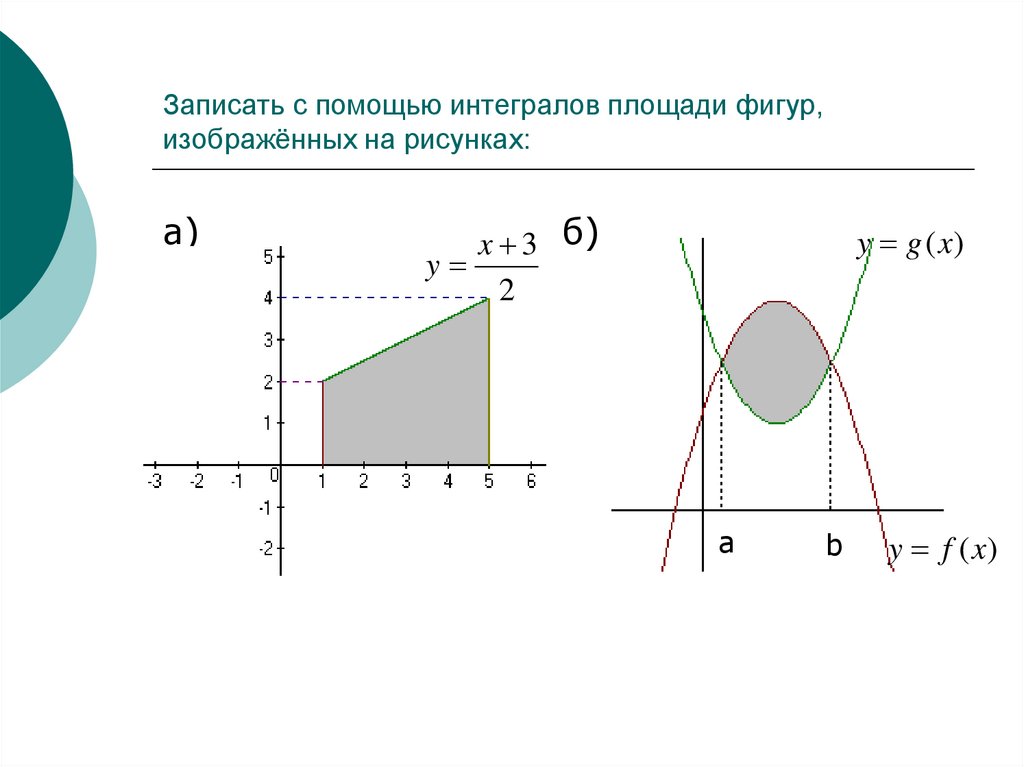
13. Записать с помощью интегралов площади фигур, изображённых на рисунках:

а)
x 3 б)
y
2
y g (x)
а
b
y f (x)

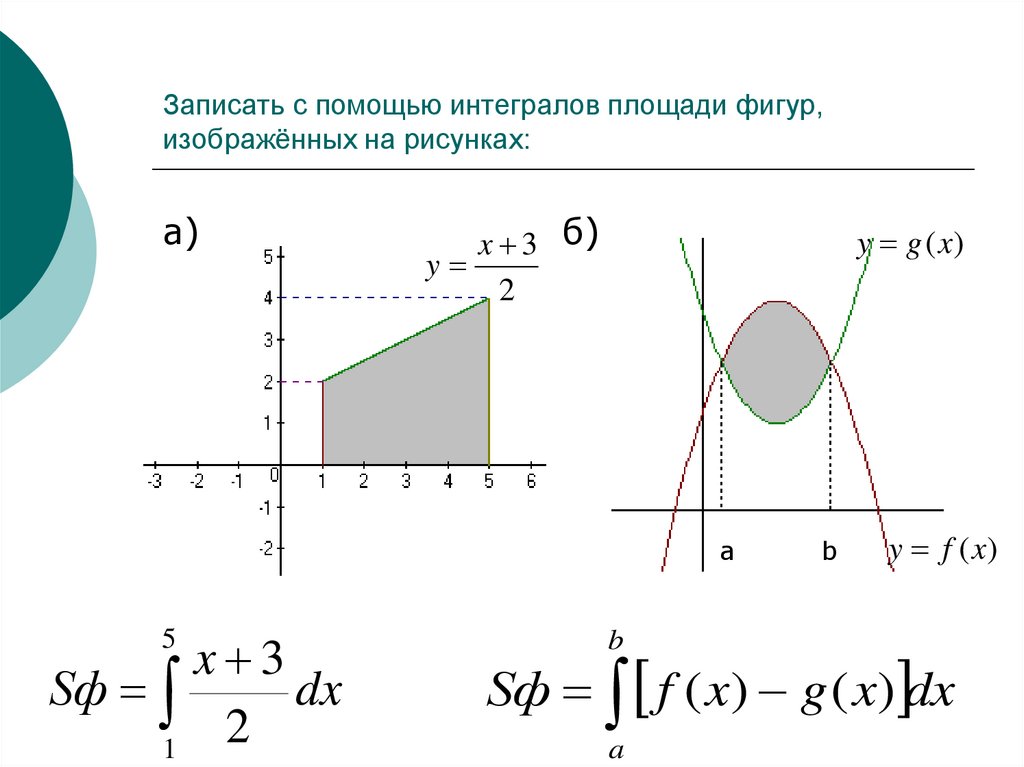
14. Записать с помощью интегралов площади фигур, изображённых на рисунках:

а)
x 3 б)
y
2
y g (x)
a
x 3
Sф
dx
2
1
5
b
b
y f (x)
Sф f ( x) g ( x) dx
a

15. Домашняя работа Нарисовать фигуры, площади которых равны следующим интегралам:

2
a)
x dx
2
0
5
4
б)
1
x dx
в)
2dx
0