Определенный интеграл. Математический анализ

1. Определенный интеграл

Математический анализ

2. Определенный интеграл

3.

4. Формула Ньютона -Лейбница

Теорема:
Если
f(x)
–
непрерывная
и
неотрицательная на отрезке [a;b] функция, а
F(x) – ее первообразная на этом отрезке, то
b
f ( x)dx F ( x) F (b) F (a)
b
a
a
По этой формуле виден порядок вычисления
определённого интеграла:
1) найти неопределённый интеграл от данной функции;
2) в полученную первообразную подставить на место
аргумента сначала верхний, а потом нижний предел
интегрирования;
3) вычислить интеграл.

5. Пример 1. Вычислить интеграл

Решение: Использовав указанные правила,
вычислим данный определённый интеграл:
ОТВЕТ:

6. Пример 2 Вычислить интеграл

7. Правила вычисления определенного интеграла

1.
2.
b
b
b
a
a
a
f ( x) g ( x) dx f ( x)dx g ( x)dx
b
b
a
a
kf ( x)dx k f ( x)dx
b
b
1
3. f (kx b)dx f (kx b)dx
ka
a

8.

9.

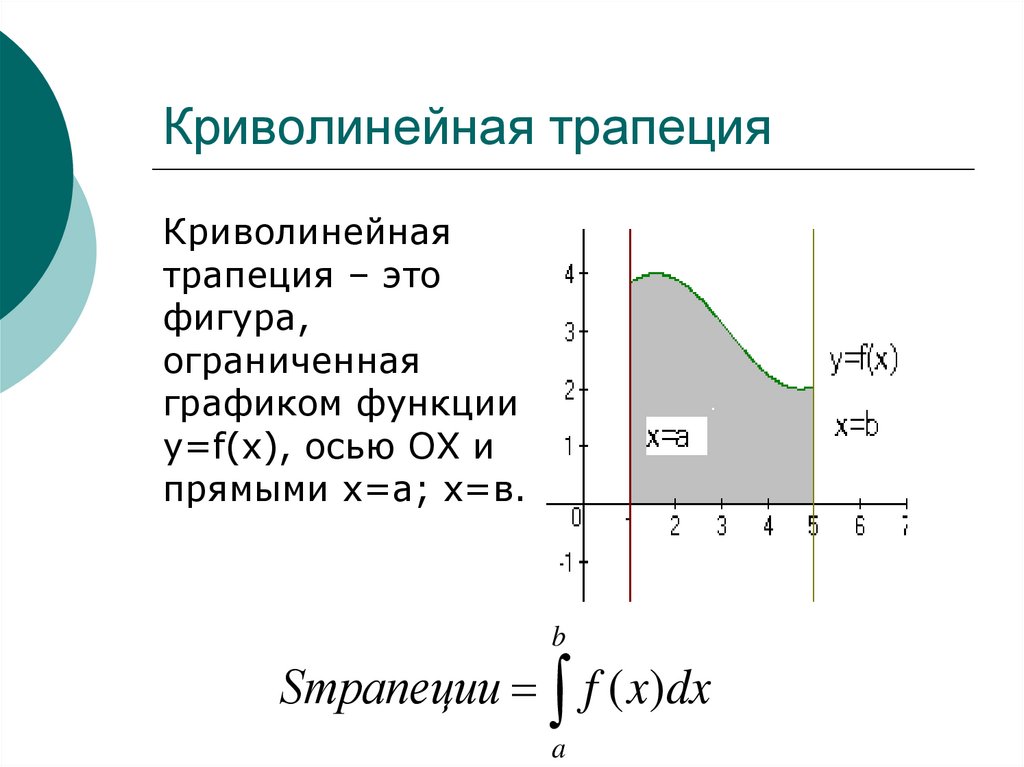
10. Криволинейная трапеция

Криволинейная
трапеция – это
фигура,
ограниченная
графиком функции
y=f(x), осью ОХ и
прямыми х=а; х=в.
b
Sтрапеции f ( x)dx
a

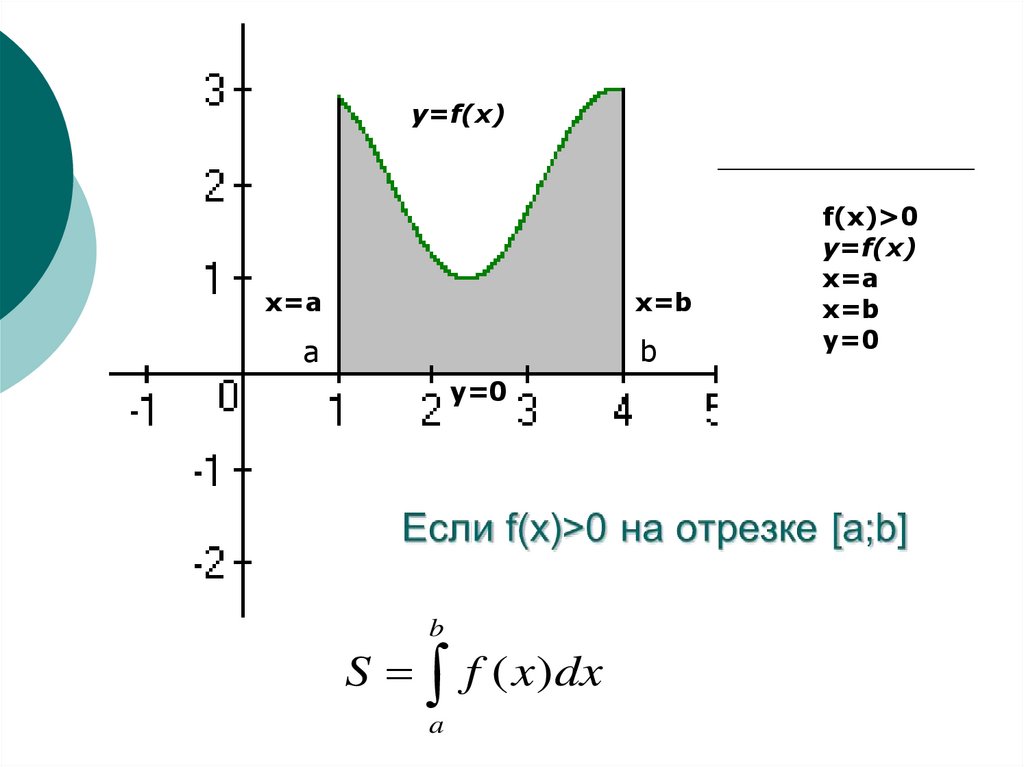
11.

y=f(x)
x=a
x=b
b
a
y=0
b
S f ( x)dx
a
f(x)>0
y=f(x)
x=a
x=b
y=0

12.

f(x)<0
x=a
x=b
y=0
a
y=0
b
x=b
x=a
y=f(x)
b
b
a
a
S f ( x)dx f ( x) dx

13.

y=f(x)
x=a
y=0
a
c
y=f(x)
x=a
x=b
y=0
b
x=b
c
b
a
c
S S1 S 2 f ( x)dx f ( x) dx

14. Пример 1

Найти площадь
фигуры, ограниченную
параболой у=х2,
прямой х=2 и осью ОХ.
y x2
x=2

15. Коротко об интеграле можно сказать так : ИНТЕГРАЛ – ЭТО ПЛОЩАДЬ криволинейной трапеции в этом заключается геометрический смысл

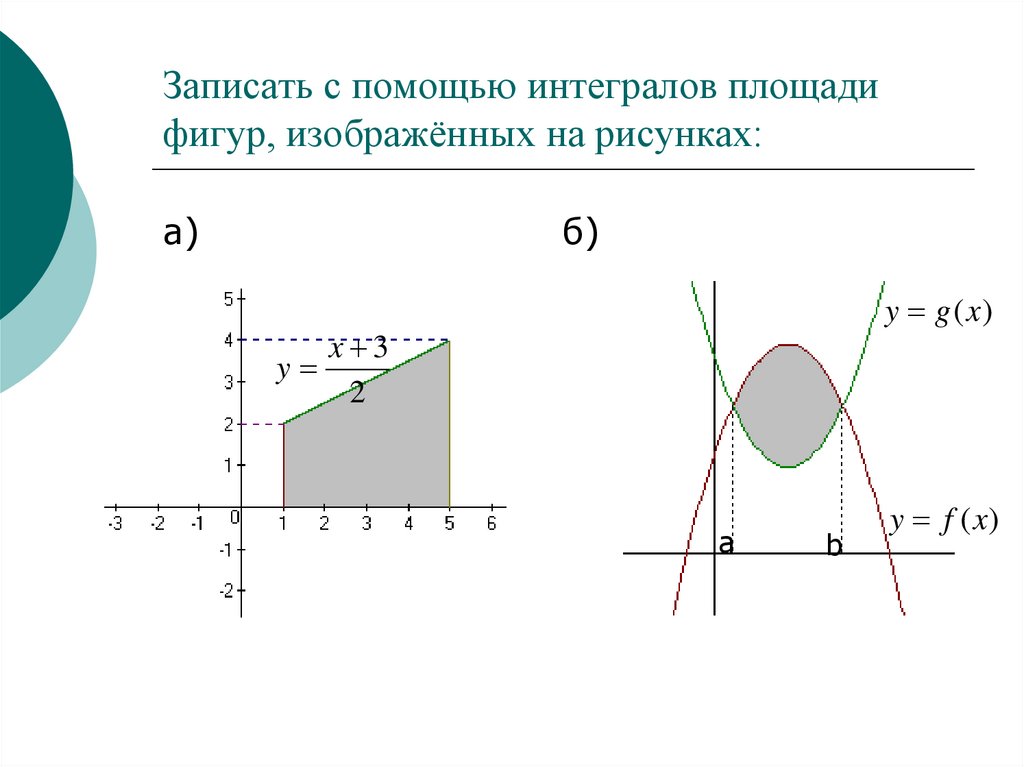
определенного интеграла

16. Записать с помощью интегралов площади фигур, изображённых на рисунках:

а)
б)
y g (x)
x 3
y
2
а
b
y f (x)

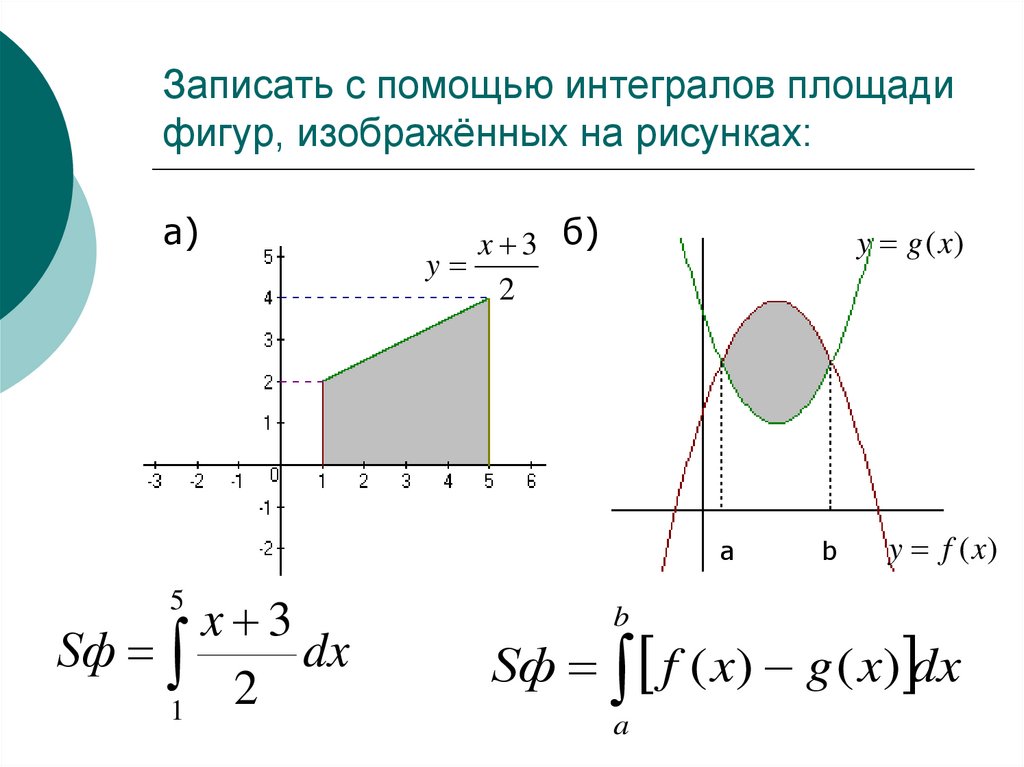
17. Записать с помощью интегралов площади фигур, изображённых на рисунках:

а)
x 3 б)
y
2
y g (x)
a
x 3
Sф
dx
2
1
5
b
b
y f (x)
Sф f ( x) g ( x) dx
a