Численное диференцирование

1. Модуль 1. Тема 2. Лекция 1. Численное дифференцирование

2. План

• Численное дифференцирование функций,
заданных аналитически
• Численное дифференцирование функций,
заданных дискретным набором данных
• Метод Рунге уточнения формул численного
дифференцирования
Литература
Формалев В. Ф., Ревизников Д. Л., Численные
методы. –М.: Физматлит, 2004. - 400 с.
Поршнев С.В., Беленкова И.В., Численные
методы на базе Mathcad. – СПб.: БХВПетербург, 2005. – 464 с.

3. Разностная схема первого порядка точности

Производная от функции
f ( x x ) f ( x )
f ( x ) lim
x 0
x
Простейшая приближенная формула
(правосторонняя разностная схема)
~
f ( x x ) f ( x )
f ( x )
x
Ряд Тейлора
f ( x )
f ( x )
f (n) ( x)
2
f ( x x ) f ( x )
x
( x ) ...
( x ) n ...
1!
2!
n!
Ошибка приближенной формулы
~
f ( x x ) f ( x )
f ( x )
f ( x )
f ( x )
x ... f ( x ) O ( x )
x
2!
Левосторонняя разностная схема первого порядка
x x :
f ( x ) f ( x x )
f ( x )
f ' ( x)
f ( x )
x ...
x
2!
Формулы точны для полиномов первой степени, т.к. для них f ( x ) 0

4. Симметричная разностная схема второго порядка

f ( x x ) f ( x x )
fˆ ( x )
2 x
Ряд Тейлора
2
3
1
x
(
x
)
(
x
)
ˆf ( x )
f ( x ) f ( x )
f ( x )
f ( x )
...
2 x
1!
2!
3!
1
x
( x ) 2
( x ) 3
f ( x ) f ( x )
f ( x )
f ( x )
...
2 x
1!
2!
3!
Ошибка приближенной формулы
f ( x )
fˆ ( x ) f ( x )
( x ) 2 ... f ( x ) O ( x ) 2
3!
Формула точна для полиномов второй степени, т.к. для них
f ( x ) 0

5. Симметричная разностная схема для второй производной

f ( x x ) 2 f ( x ) f ( x x )
fˆ ( x )
x 2
Ряд Тейлора
2
3
4
x
(
x
)
(
x
)
(
x
)
IV
x fˆ ( x ) f ( x ) f ( x )
f ( x )
f ( x )
f ( x)
...
1!
2!
3!
4!
2
x
( x ) 2
( x ) 3
( x ) 4
IV
2 f ( x ) f ( x ) f ( x )
f ( x)
f ( x)
f ( x)
...
1!
2!
3!
4!
Ошибка приближенной формулы
IV
f
( x)
fˆ ( x ) f ( x )
( x ) 2 ... f ( x ) O ( x ) 2
12
Формула точна для полиномов третьей степени, т.к. для них f
IV
( x) 0
f ( x x ) f ( x ) f ( x ) f ( x x ) fˆ x x fˆ x x
Альтернативная
2
2
x
x
ˆ ( x )
f
идея вывода
x
x
Схемы для производных более высоких порядков можно строить аналогично

6.

Пример
Продифференцировать численно функцию
sin 0.01x 2 , 0 x 10
с применением правосторонней и симметричной разностных формул
для первой производной на равномерной сетке. Сопоставить ошибки
приближенных формул численного дифференцирования.

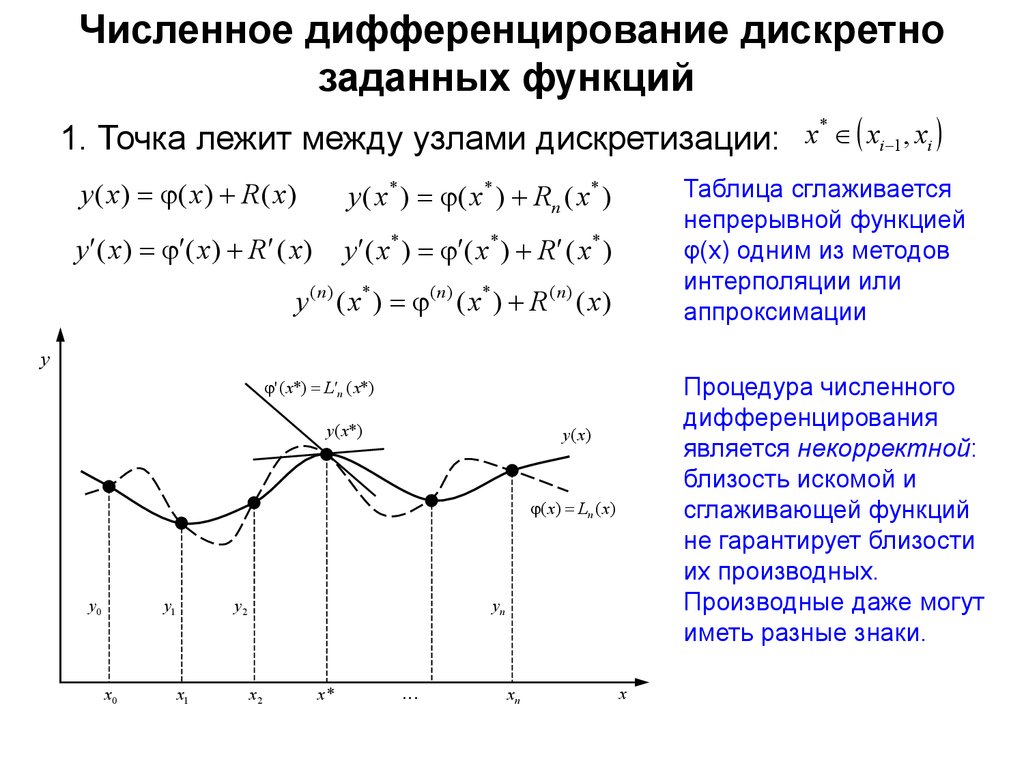
7. Численное дифференцирование дискретно заданных функций

*
x
xi 1 , xi
1. Точка лежит между узлами дискретизации:
y ( x ) ( x ) R ( x )
y ( x * ) ( x * ) Rn ( x * )
y ( x ) ( x ) R ( x )
y ( x * ) ( x * ) R ( x* )
Таблица сглаживается
непрерывной функцией
φ(x) одним из методов
интерполяции или
аппроксимации
y ( n ) ( x * ) ( n ) ( x * ) R ( n ) ( x )
y
Процедура численного
дифференцирования
является некорректной:
близость искомой и
сглаживающей функций
не гарантирует близости
их производных.
Производные даже могут
иметь разные знаки.
' ( x* ) L' n ( x* )
y ( x* )
y (x)
( x) Ln ( x)
y0
y1
x0
y2
x1
yn
x2
x*
xn
x

8.

Численное дифференцирование дискретно
заданных функций
2. Точка совпадает с одним из узлов:
h2
h3
yi 1 y ( xi h ) yi yi h yi yi
2
6
h2
h3
yi 1 y ( xi h ) yi yi h yi yi
2
6
y yi
y
yi i 1
O (h ) i O (h )
h
h
y yi 1
y
yi i
O(h) i O(h)
h
h
yˆ i
yi 1 yi 1
yˆ
O (h 2 ) i O (h 2 )
2h
2h
h4
y ( )
24
4
h
y IV ( )
24
IV
x* xi , i 1, n 1
Можно использовать
аппарат разложения
функций в ряд Тейлора
Отношение конечных разностей справа
Отношение конечных разностей слева
Отношение центральных разностей
Порядком точности метода численного дифференцирования называют
показатель степени h в главном члене погрешности

9.

Численное дифференцирование дискретно
заданных функций
Вторая производная
2
yi 1 2 yi yi 1
yi
2
2
yˆ i
O
(
h
)
O
(
h
)
2
2
h
h
Центральные разности
Третья производная
3 yi yi 2 3 yi 1 3 yi yi 1
yi 3
O(h)
3
h
h
3 yi yi 1 3 yi 3 yi 1 yi 2
yi 3
O (h )
3
h
h
Правосторонние разности
Левосторонние разности
Используется 4 узла сетки
yˆ i
1
y 2 yi 1 2 yi 1 yi 2
2
( yi yi ) i 2
O
(
h
)
3
2
2h
Центральные разности
Фактически, используется 5 узлов
yiIV
yi 2 4 yi 1 6 y i 4 yi 1 yi 2
2
O
(
h
)
4
h
Четвертая производная

10.

Метод Рунге уточнения формул
численного дифференцирования
f ( x ) h ( x ) h p ( x ) O ( h p 1 ) O ( h p 2 ) ...
R p h p ( x ) O ( h p 1 ) O ( h p 2 ) ...
f ( x ) h ( x )
Метод p-го порядка
Остаточный член
Вычисляем разностную производную на
равномерной сетке с шагом h
Вводим более подробную сетку с шагом kh (k = 1/2;1/4;1/8; … )
f ( x ) kh ( x ) ( kh ) p ( x ) O ( h p 1 ) Производная на сетке с шагом kh
h ( x ) kh ( x )
p 1
Главный член погрешности в
O
(
h
)
узлах исходной сетки
k p 1
p h ( x ) kh ( x )
p 1
Метод (p+1)-го порядка
f ( x ) kh ( x ) k
O
(
h
)
p
k 1
в узлах исходной сетки
p h ( x ) kh ( x )
Уточненная разностная
f ( x ) kh ( x ) k
p
k 1
аппроксимация
h p ( x )