Численное решение уравнения колебаний струны

1. Лабораторная №9. Численное решение уравнения колебаний струны

2.

Дифференциальное уравнение в частных
производных
(ДУЧП)
содержит
неизвестные
функции
нескольких
переменных и их частные производные.
Важные частные случаи уравнений в
частных производных рассматриваются в
курсе математической физики и потому
еще
называются
уравнениями
математической физики.
2

3. ДУЧП с двумя переменными

Разработаны численные методы решения ДУЧП,
применимые к широким классам уравнений и
различным типам задач для них.
Ограничимся наиболее распространенными и
хорошо изученными задачами для уравнений
первого и второго порядков, линейных
относительно производных, а также случаем двух
переменных. Общий вид такого ДУЧП:
u u u u u
F ( x, y , u , , , 2 , 2 ,
) 0
x y x y x y
2
2
2
3

4.

Решением этого уравнения является
функция u ( x, y ) ,
описывающая
некоторую поверхность в трехмерном
пространстве.
Линейное относительно производных
уравнение:
u
u
u
u
u
A 2 2B
C 2 a
b c f
x y
x
y
x
y
2
2
2
где коэффициенты, вообще говоря, тоже
являются функциями x, y и u.
4

5. Классификация ДУЧП 2-го порядка

u
u
u
u
u
A 2 2B
C 2 a
b c f
x y
x
y
x
y
2
2
2
Такие уравнения классифицируются
по знаку дискриминанта B2–AC:
• B2–AC>0 – гиперболические,
• B2–AC=0 – параболические,
• B2–AC<0 – эллиптические уравнения.
5

6. Разностные методы

• Как и в случае ОДУ, для применения
разностного метода в области изменения
переменных D вводят некоторую сетку.
• Все производные, входящие в уравнение
и краевые условия, заменяют разностями
(или
другими
алгебраическими
комбинациями) значений функции u(x,y) в
узлах сетки. Получающиеся при этом
алгебраические
уравнения
называют
разностной схемой.
6

7.

• Конфигурацию узлов, используемую для
составления разностной схемы, называют
шаблоном.
• Решая алгебраическую систему, полученную на
шаблоне, находят приближенное (разностное)
решение в узлах сетки.
• Для большинства разностных схем узлы сетки
лежат на пересечении некоторых прямых линий
(гиперплоскостей),
проведенных
либо
в
естественной системе координат, либо в
специально подобранной по форме области D.
7

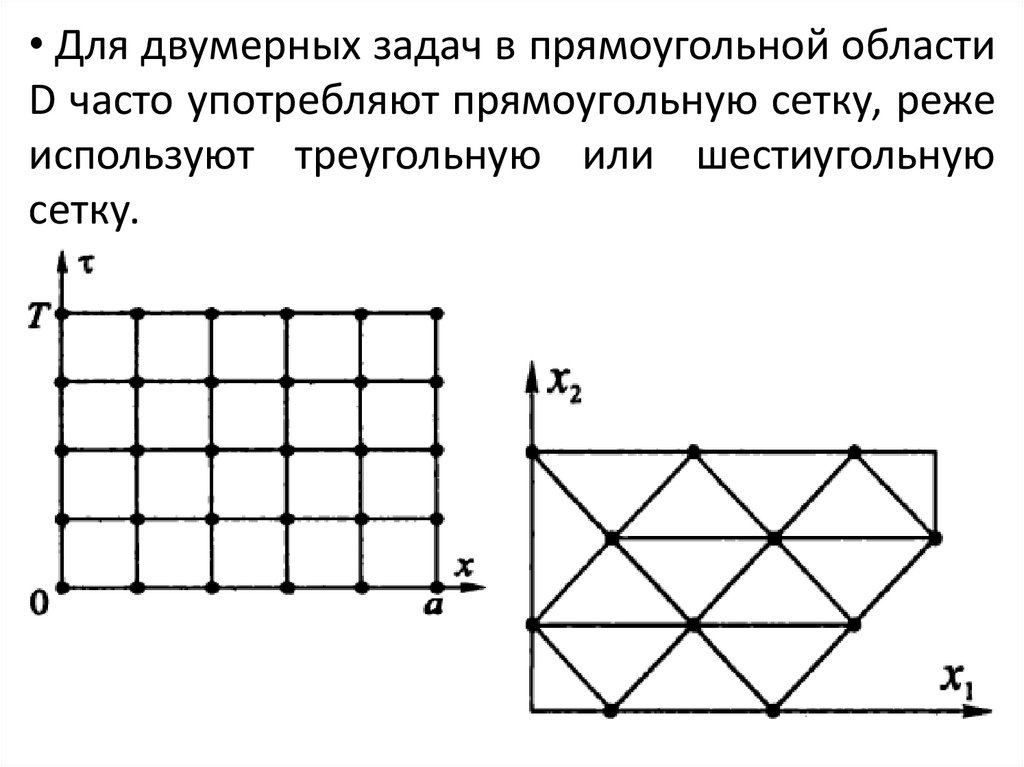
8.

• Для двумерных задач в прямоугольной области
D часто употребляют прямоугольную сетку, реже
используют треугольную или шестиугольную
сетку.
8

9. Гиперболические уравнения

К гиперболическим уравнениям приводят задачи
колебания струны, движения сжимаемого газа,
распространения электромагнитных волн и др.
Одномерное волновое уравнение (уравнение
малых колебаний натянутой невесомой струны):
u ( x, t )
2
t 2
2 u ( x, t )
a
2
2
x
a const
u ( x,0) ( x)
u ( x, t )
( x)
t t 0
x [0, a]
u (0, t ) 1 (t )
u (a, t ) 2 (t )
t [0,T ]
9

10.

Задачу можно решать по схеме с шаблоном типа
«крест»
ui , j 1 2ui , j ui , j 1
2
2 ui 1, j 2ui , j ui 1, j
a
2
h
Отсюда трехслойная схема расчета, в которой
значения в данном слое вычисляются по двум
предыдущим:
ui, j 1 2(1 )ui, j (ui 1, j ui 1, j ) ui, j 1
10

11.

a
2
2
Здесь
–
параметр,
h2
определяемый соотношением шагов сетки.
Граничные условия, как и прежде, определяют
значения решения в начальных точках сетки:
u0, j 1 (t j )
un, j 2 (t j )
j 0,1,2,...
11

12.

Начальные условия определяют значения
решения в двух первых слоях сетки по
времени, т.е. при
j 0,1
Решение в первом слое определяется
непосредственно из первого начального
условия:
ui ,0 ( xi )
i 1, n 1
12

13.

Для определения решения во втором слое
нужно аппроксимировать производную из
второго начального условия. Простейший
способ сделать это:
ui ,1 ui ,0
u ( x, t )
( xi )
t t 0
Отсюда
ui ,1 ui,0 ( xi )
i 1, n 1
13

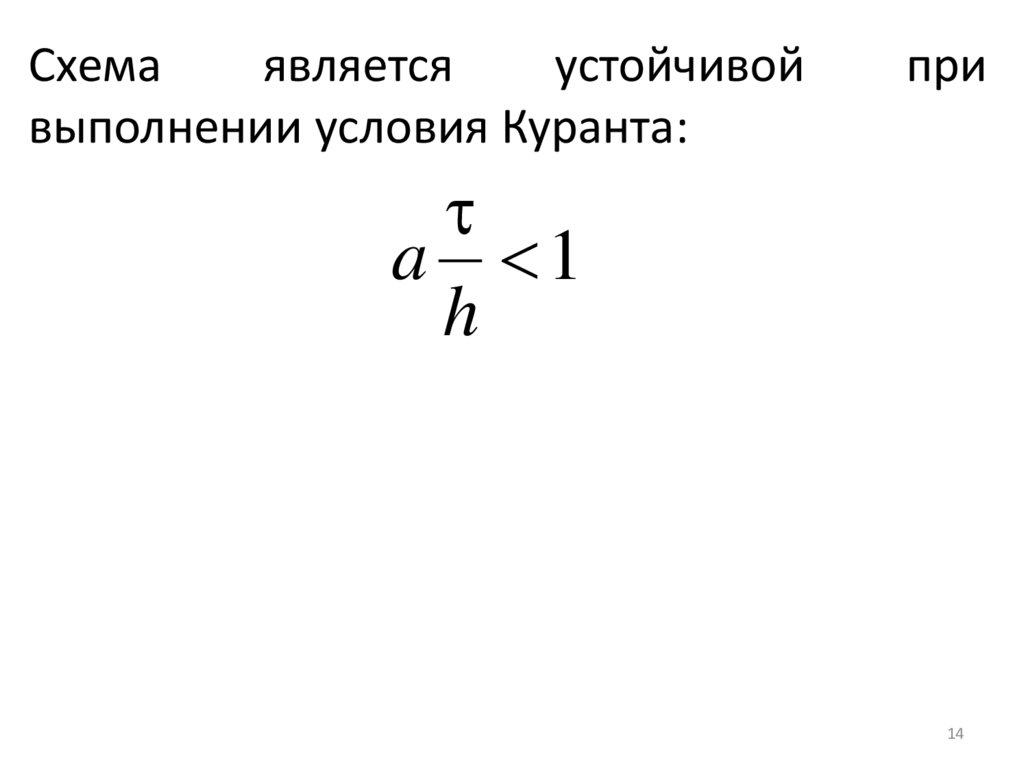
14.

Схема
является
устойчивой
выполнении условия Куранта:
при
a 1
h
14

15. Задание

1. Реализовать численную схему решения
уравнения колебаний струны (одномерного
волнового уравнения) с использованием
шаблона «крест».
2. Решение отобразить графически в виде
зависимости u от x в различные моменты
времени.
3. Начальные и граничные условия могут быть
разными. Как вариант: закрепленная на концах
струна, в начальный момент неподвижная и
отклоненная каким-либо образом (напр., синус).