Похожие презентации:
Выпуклый анализ. Теория двойственности в линейном программировании. Лекция 28
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 2811. ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМ
ПРОГРАММИРОВАНИИ
2.
11. ТЕОРИЯ ДВОЙСТВЕННОСТИ В ЛИНЕЙНОМПРОГРАММИРОВАНИИ
11.1. Двойственная задача к канонической задаче линейного
программирования.
11.2. Двойственная задача к стандартной задаче линейного
программирования.
11.3. Двойственная задача к общей задаче линейного
программирования.
11.4. Правило построения двойственной задачи.
3.
11.1. Двойственная задача к канонической задаче линейного программирования.Рассмотрим каноническую задачу линейного программирования.
I ( u ) = c, u ® inf,
Задача 1.
u Î U = { u Î U 0 Au - b = 0} ,
Здесь
{
}
U0 = u Î Rn u ³ 0 ,
A ¸ s ´ n, b Î R s , c Î R n , L 0 = R s .
Построим функцию Лагранжа для задачи 1. Имеем
L ( u , l ) = c, u + l , Au - b = c, u + l , Au - l , b =
= c, u + AT l , u - l , b =
Функция
y :L ® R ,
0
1
определяемая формулой
здесь выписывается в явном виде. Действительно,
c + AT l , u - l , b .
æ ³0 ö
y ( l ) = inf L ç u , l ÷ ,
uÎU 0
è
ø
ìï- b, l ,
c + AT l ³ 0;
y ( l) = í
i
T
$i Î { 1,L , s} : ( c + A l ) < 0.
ïî -¥,
4.
Таким образом, точкаy
на которой может достигаться максимум функции
ìï- b, l ,
c + AT l ³ 0;
y ( l) = í
i
T
$i Î { 1,L , s} : ( c + A l ) < 0
ïî -¥,
среди тех векторов
задача
l * Î L0 ,
l ÎL
0 для которых выполнено
y ( l ) ® sup,
l Î L0
c + AT l ³ 0.
{
Двойственная
формулируется так.
-b, l ® sup,
Задача 1д.
следует искать
} {
}
l Î L = l Î R s c + AT l ³ 0 = l Î R s - AT l - c £ 0 .
Данная задача эквивалентна следующей.
Задача 1д(а).
{
b, l ® inf,
}
l Î L = l Î R s - AT l - c £ 0 .
Эквивалентность задачи 1д и задача 1д(а) понимается в том смысле, что их
решениями служат одни и те же точки
двойственной к задаче 1.
l * Î L.
Задачу 1д(а) обычно называют
5.
Задача 1д(а). является задачей линейного программированиянеравенств. Матрица ограничений
- AT
n ´ s.
имеет размер
Нельзя считать стандартной, т.к. компоненты вектора
Покажем, что задача двойственная к задаче 1д(а),
задачи 1д(а)
æ u1 ö
ç ÷
Полагаем u = ç L ÷ . Тогда
ç un ÷
è ø
Заметим, что эту задачу
l не обязаны быть положительными.
будет эквивалентна задаче 1.
Обозначим множители Лагранжа в задаче 1д(а) символами
функцию Лагранжа для
с ограничениями типа
u1 ,L , u n . Составим
Задача 1д(а)
b, l ® inf,
{
}
l Î L = l Î R s - AсT l - £ 0
L Д ( l , u ) = b, l + u , - AT l - c = b, l - u, c + u , - AT l =
= b, l - u , c - Au , l = b - Au , l - c, u
е
основные
47 4 4
4 48
6 4 4 44
7 4 4 4 48 6 4 4 4двойственны
Здесь
U 0 Д = { l l Î R s } = L 0 , L 0Д = u Î R n u ³ 0 = U 0 ,
{
}
6.
L Д ( l , u ) = b - Au , l - c, uТогда
ÎR s
é
ù
y Д ( u ) = inf L Д ( l , u ) = infs ê b - Au, l - c, u ú =
lÎR
lÎU 0 Д
ë
û
ì- c, u , b - Au = 0;
=í
b - Au ¹ 0.
î -¥,
Задача двойственная к задаче 1д(а)
y Д ( u ) ® sup,
(Задача 1д(а))д.
{
{
}
u Î L 0Д = U 0 = u Î R n u ³ 0
-c, u ® sup,
Задача 1.
}
u Î u Î R b - Au = 0; u ³ 0 = U .
n
(Задача 1д(а))д(а).
c, u ® inf,
{
}
тождественны.
c, u ® inf,
u = { u Î U 0 Au - b = 0} ,
{
}
U0 = u Î Rn u ³ 0 .
u Î u Î R n b - Au = 0; u ³ 0 = U .
Задачи 1 и (1д(а))д(а)
имеет вид
7.
11.2. Двойственная задача к стандартной задаче линейного программирования.Рассмотрим стандартную задачу линейного программирования.
Задача 2.
c, u ® inf,
{
}
u Î U = { u Î U 0 Au - b £ 0} ,
U0 = u Î Rn u ³ 0 ,
Здесь
{
}
0
m
L
=
l
Î
R
l³0
A ¸ m ´ n, b Î R , c Î R ,
m
n
Построим функцию Лагранжа для задачи 2. Имеем
L ( u , l ) = c, u + l , Au - b = c, u + l , Au - l , b =
= c + AT l , u - l , b .
Функция
y : L 0 ® R1 ,
определяемая формулой
y ( l ) = inf L ( u, l ) ,
uÎU 0
здесь выписывается в явном виде. Действительно,
ìï- b, l ,
c + AT l ³ 0;
y ( l) = í
i
T
$i Î { 1,L , m} : ( c + A l ) < 0.
ïî -¥,
8.
l * Î L 0 , на которой может достигаться максимум функцииìï - b, l ,
c + AT l ³ 0;
y ( l) = í
i
T
$i Î { 1,L , m} : ( c + A l ) < 0.
ïî -¥,
Таким образом, точка
y
следует искать среди тех векторов l Î L 0
c + A l ³ 0.
T
Двойственная задача
{
}
= l Î Rm l ³ 0 ,
для которых выполнено
{
}
y ( l ) ® sup, l Î L 0 = l Î R m l ³ 0
формулируется так.
Задача 2д.
-b, l ® sup,
} {
{
}
m
T
l Î L = l Î R m c + AT l ³ 0, l Î L 0 = l Î R - A l - c £ 0, l ³ 0 .
Данная задача эквивалентна следующей.
Задача 2д(а).
b, l ® inf ,
{
}
l Î l Î R m - AT l - c £ 0, l ³ 0 .
9.
Эквивалентность Задачи 2д и Задача 2д(а)Задача 2д(а)
понимается в том смысле, что их решениями служат
b, l ® inf ,
{
}
одни и те же точки
l * Î L.
Задачу 2д(а) обычно
l Î l Î R m - AT l - c £ 0, l ³ 0 называют двойственной к Задаче 2.
Задача 2д(а). является стандартной задачей линейного программирования. Матрица
ограничений имеет размер
n ´ m.
Покажем, что задача двойственная к задаче 2д(а) будет эквивалентна задаче 2.
Обозначим множители Лагранжа в задаче 2д(а) символами
u1 , L , u n .
Составим функцию Лагранжа для задаче 2д(а).
æ u1 ö
ç ÷
u
=
Полагаем
ç L ÷ .Тогда
ç un ÷
è ø
L Д ( l , u ) = b, l + u , - AT l - c = b - Au , l - c, u .
Здесь
основные
644444
7 4 4 4 4 48
U0 Д = l Î l Î Rm l ³ 0 = L0 ,
{
Тогда
}
е
6 4 4 4двойственны
47 4 4
4 48
L 0Д = u Î R n u ³ 0 = U 0 .
{
}
L Д ( l , u ) = b - Au , l - c, u
y Д ( u ) = inf L Д ( l , u ) =
lÎU 0 Д
{
infm
}
lÎ lÎR l ³ 0
éë b - Au , l - c, u ùû =
10.
={
infm
}
lÎ lÎR l ³ 0
éë b - Au , l - c, u ùû =
ìb - Au ³ 0;
ï c, u ,
=í
=y Д ( u)
i
T
$i Î { 1,L , m} : ( c + A l ) < 0
ïî -¥,
u Î L 0Д = U 0 = u Î R n u ³ 0
Задача двойственная к задаче 2д(а) y Д ( u ) ® sup,
{
имеет вид.
}
Задача 2
(Задача 2д(а))д.
c, u ® inf,
-c, u ® sup,
u Î u Î R n Au £ b; u ³ 0 = U . U = u Î R n u ³ 0 ,
0
{
}
{
u Î { u Î U 0 Au - b £ 0} .
(Задача 2д(а))д(а).
c, u ® inf,
{
}
u Î u Î R n Au £ b; u ³ 0 = U .
Задачи 2 и (2д(а))д(а) тождественны.
}
11.
11.3. Двойственная задача к общей задаче линейного программирования.Рассмотрим общую задачу линейного программирования.
Задача 3.
c, u ® inf,
ìï
üï
æ wö
ˆ
ˆ
u Î U = íu = ç ÷ Î U 0 Au - b £ 0, Au - b = 0 ý ,
è wø
îï
þï
Здесь
æ u1 ö
æ u k +1 ö
ç ÷
ç
÷
k
w = ç L ÷ Î R , w = ç L ÷ Î R n - k , k £ n,
ç uk ÷
ç un ÷
è ø
è
ø
A ¸ m ´ n, Aˆ ¸ ( s - m ) ´ n,
b Î R m , bˆ Î R s -m , c Î R n .
ìï
æ wö
U 0 = íu = ç ÷ Î R n w ³ 0,
è wø
ïî
üï
ý.
ïþ
12.
Полагаемæ l1 ö
æ lm +1 ö
ìï
üï
ç ÷
ç
÷
æmö
m
s-m
0
s
m
=
L
Î
R
,
m
=
L
Î
R
L = íl = ç ÷ Î R m ³ 0 ý ,
ç ÷
ç
÷
m
çl ÷
ç l ÷
è ø
ïî
ïþ
è mø
è s ø
Построим функцию Лагранжа для задачи 3.
Имеем
ˆ - bˆ =
L ( u , l ) = c, u + m , Au - b + m , Au
ˆ - m , bˆ =
= c, u + m , Au - m , b + m , Au
= c, u + AT m , u - m , b + Aˆ T m , u - m , bˆ =
bö æ m ö
æ
w
æ
ö
= c + A m + Aˆ m , ç ÷ - çç ÷÷ , ç ÷ ,
ˆ
è wø
èbø è m ø
T
T
е
ые
47 4 4
4 4 48
6 4 4 4 4 4основн
74
4 4 4 4 8 6 4 4 4 4двойственны
ìï
üï
ìï
üï
æmö
æ wö
0
s
n
u Î U 0 = íu = ç ÷ Î R w ³ 0 ý , l Î L = íl = ç ÷ Î R m ³ 0 ý .
è wø
èmø
ïî
ïþ
ïî
ïþ
13.
Функцияy : L 0 ® R1 ,
определяемая формулой
y ( l ) = inf L ( u, l ) ,
здесь выписывается в явном виде. Действительно,
æbö æ m ö
æ wö
T
ˆ
L ( u , l ) = c + A m + A m , ç ÷ - çç ÷÷ , ç ÷ ,
ˆ
è wø
èbø è m ø
T
ì
ï
ï=í
ï
ï
î
ìï
üï
æ wö
u Î U 0 = íu = ç ÷ Î R n w ³ 0 ý ,
è wø
îï
þï
ìï
üï
æmö
l Î L 0 = íl = ç ÷ Î R s m ³ 0 ý
èmø
îï
þï
æbö æ m ö
æ wö
T
ˆ
c + A m + A m , ç ÷ - çç ÷÷ , ç ÷ =
ˆ èmø
b
è wø
è ø
y ( l ) = inf L ( u, l ) = winf
³0
uÎU 0
uÎU 0
T
wÎR s -m
(
)
ì c + AT m + Aˆ T m j ³ 0, j Î 1,L , k ,
{
}
æbö æ m ö
ï
çç ˆ ÷÷ , ç ÷ , í
j
m
T
T
b
ˆ
è
ø
è ø
ï c + A m + A m = 0, j Î { k + 1,L , n} ;
î
-¥,
при остальных l Î L 0
(
)
14.
y ( l ) ® sup,Двойственная задача:
ìï
üï
æmö
m
s-m
l Î L = íl = ç ÷ Î R ´ R m ³ 0 ý
èmø
ïî
ïþ
0
ì
ï
ïy ( l) = í
ï
ï
î
(
)
ì c + AT m + Aˆ T m j ³ 0, j Î { 1,L , k } ,
æbö æ m ö
ï
çç ˆ ÷÷ , ç ÷ , í
j
èbø è m ø
ï c + AT m + Aˆ T m = 0, j Î { k + 1,L , n} ;
î
записывается в виде
-¥,
при остальных l Î L 0
(
Задача 3д.
(
)
æbö æ m ö
- çç ÷÷ , ç ÷ ® sup
ˆ èm ø
b
è ø
j
T
T
c + A m + Aˆ m ³ 0, j Î { 1,L , k } ;
)
( c + A m + Aˆ m )
T
T
j
= 0,
j Î { k + 1,L , n} ;
ìï
üï
æmö
m
s -m
l Î L = íl = ç ÷ Î R ´ R m ³ 0 ý .
èmø
ïî
ïþ
0
15.
Данная задача эквивалентна следующей.Задача 3д(а).
æbö æ m ö
çç ˆ ÷÷ , ç ÷ ® inf,
èbø è m ø
(
-c - A m - Aˆ T m
T
( -c - A m - Aˆ m )
T
T
j
)
j
£ 0,
= 0,
j Î { 1,L , k } ;
j Î { k + 1,L , n} ;
ìï
üï
æmö
m
s-m
l Î L = íl = ç ÷ Î R ´ R m ³ 0 ý .
èm ø
ïî
ïþ
0
Эквивалентность задачи 3д и задача 3д(а) понимается в том смысле, что их
решениями служат одни и те же точки
l * Î L.
Задачу 3д(а) обычно называют
двойственной к задаче 3. Задача 3д(а). является общей задачей линейного
программирования. Матрица ограничений в ней имеет размер n ´ s.
По аналогии с предыдущими пунктами доказывается, что Задачи 3 и (Задача 3д(а))д
эквивалентны.
16.
11.4. Правило построения двойственной задачи. Запишем задачу 3 и задачу 3д(а)в координатной форме.
Задача 3.
I ( u ) = c1u1 + L + ck u k + ck +1u k +1 + L + cnu n ® inf,
a11u1 + L + a1k u k + a1k +1u k +1 + L + a1nu n £ b1 ,
L L L L L L L L L L L L L L L L L
am1u1 + L + amk u k + amk +1u k +1 + L + amnu n £ bm ,
am +11u1 + L + am +1k u k + am +1k +1u k +1 + L + am +1nu n = bm +1 ,
L L L L L L L L L L L L L L L L L L L L L
as1u1 + L + ask u k + ask +1u k +1 + L + asnu n = bs ,
u1 ³ 0,L , u k ³ 0.
17.
Задача 3д(а).I Д ( l ) = b1l1 + L + bm lm + bm +1lm +1 + L + bs ls ® inf,
- a11l1 - L - am1lm - am +11lm +1 - L - as1ls £ c1 ,
L L L L L L L L L L L L L L L L L L L
- a1k l1 - L - amk lm - am +1k lm +1 - L - ask ls £ ck ,
-a1k +1l1 - L - amk +1lm - am +1k +1lm +1 - L - ask +1ls = ck +1 ,
L L L L L L L L L L L L L L L L L L L L L L
-a1n l1 - L - amn lm - am +1n lm +1 - L - as n ls = cn ,
l1 ³ 0,L , lm ³ 0.
Сформулируем правило, в соответствие с которым строится задача 3д(а), на основе
задачи 3.
18.
В двойственной задаче 3д(а) переменныхl j , j = 1,L , s
столько же, сколько
ограничений в прямой задаче 3. Матрица ограничений в двойственной задаче совпадает
с транспонированной матрицей
æ Aö
ç ˆ÷
è Aø
ограничений прямой задачи, умноженной на
( -1) .
Вектором правых частей ограничений двойственной задачи служит вектор коэффициентов
целевой функции прямой задачи. В качестве вектора целевой функции
двойственной задачи выступает вектор
æbö
çç ˆ ÷÷
èbø
правых частей ограничений прямой задачи.
Ограничения двойственной задачи, номера которых совпадают с номерами положительных
переменных прямой задачи, записываются в форме неравенств, а остальные ограничения –
в форме равенств. Наконец, переменные двойственной задачи, номера которых совпадают
с номерами ограничений типа неравенств в прямой задаче, объявляются положительными,
а на остальные переменные ограничения не налагаются.
19.
Пример 1.Прямая задача.
I ( u1 , u 2 , u 3 , u 4 , u 5 ) = -40u1 + 7u 2 - 3u 3 + 6u 4 - 3u 5 ® inf,
4u1 + u 2 + 2u 3 + u 4 + 3u 5 £ 55,
-17u1 + 16u 2 - 4u 3 + 2u 4 + 5u 5 = 46,
-33u1 + 26u 2 - 7u 3 + 4u 4 + 8u 5 = 66,
u1 ³ 0, u 2 ³ 0, u 3 ³ 0.
Двойственная задача.
I Д ( l 1, l 2, l 3 ) = 55l 1+ 46l 2 + 66l 3® inf
-4l 1+ 17l 2 + 33l 3£ -40,
-l 1- 2l 2 - 4l 3= 6,
-l 1- 16l 2 - 26l 3£ 7,
-2l 1+ 4l 2 + 7l 3£ -3,
-3l 1- 5l 2 - 8l3 = -3,
l 1³ 0.











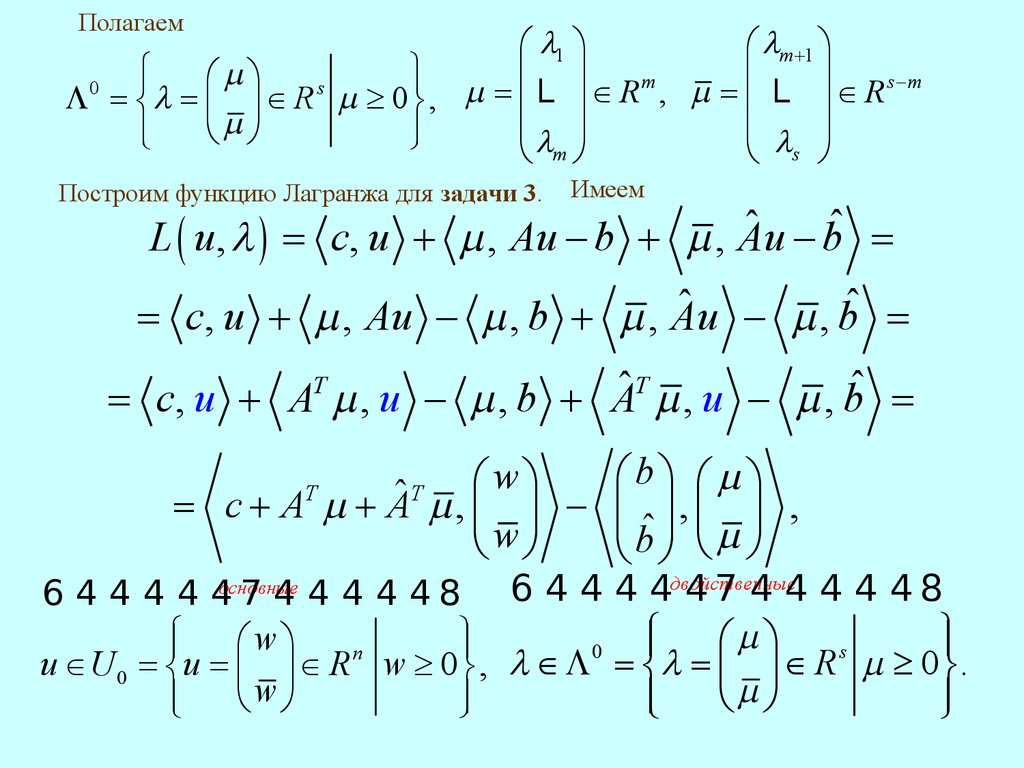
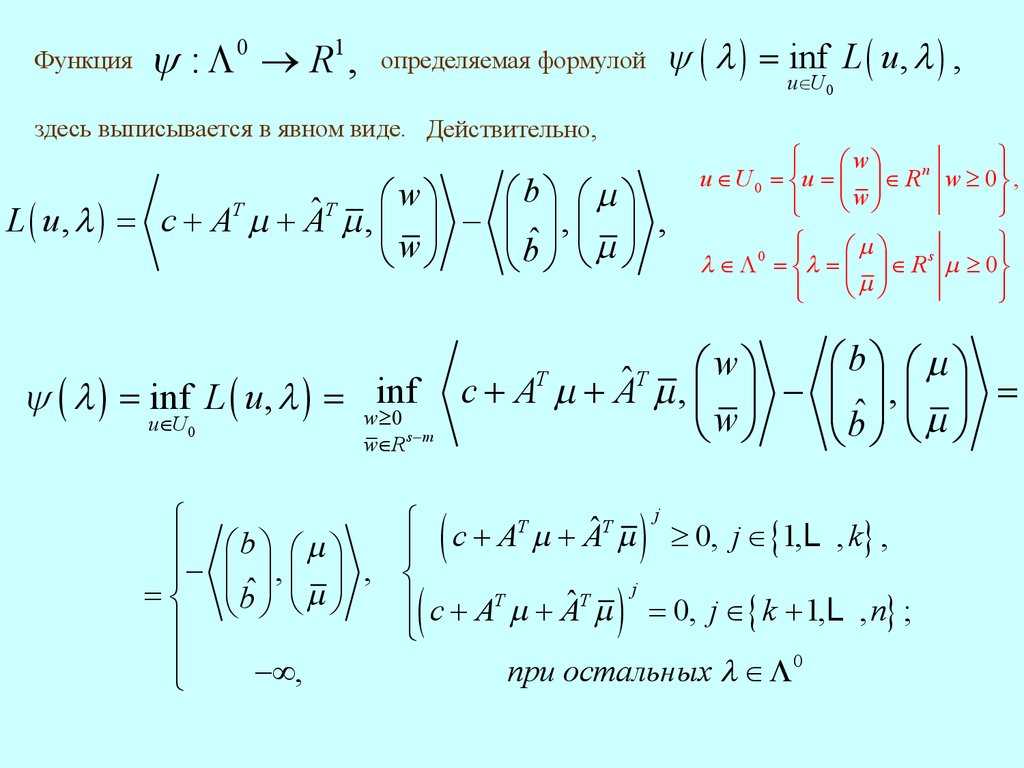





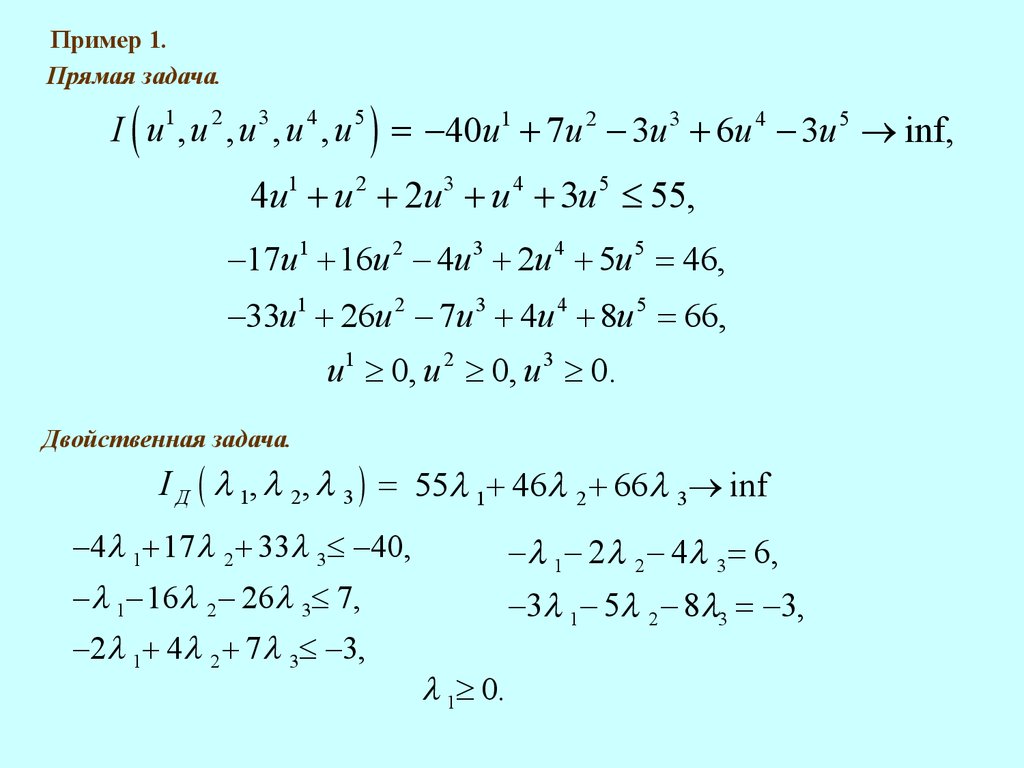


 Математика
Математика Программирование
Программирование








