Похожие презентации:
Выпуклый анализ. Субградиент и субдифференциал функции. Лекция 20
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 207. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ
2.
7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ7.1. Определение субградиента и субдифференциала функции. Примеры.
3.
7. СУБГРАДИЕНТ И СУБДИФФЕРЕНЦИАЛ ФУНКЦИИ7.1. Определение субградиента и субдифференциала функции. Примеры.
Определение 1. Пусть
I :U R1 , U R n
называется субградиентом функции
I
в точке
v,
и
v ÎU .
Вектор
c( v ) Î R n
если
I (u ) ³ I (v) + c(v), u - v , "u Î U .
Множество всех субградиентов функции
субдифференциалом этой функции в точке
I ( u)
I ( v)
O
I
v
в точке
v
(1)
называют
и обозначают символом
¶I (v).
Геометрический смысл неравенства (1) состоит в том,
что график функции
I = I ( u)
l = l ( u)
j tgj = c ( v )
v
лежит не ниже графика
l : R n R1 , определенной
l (u ) = I (v) + c(v ), u - v , u Î U .
l (v) = I (v).
линейной функции
равенством
u
I
При этом
Понятие субградиента и субдифференциала определено для произвольной функции
I : R n R1 .
Однако естественным это понятие является для выпуклых функций.
4.
Для выпуклых дифференцируемых функций был установлен критерий выпуклостиI (u ) ³ I (v) + I '(v ), u - v , "u Î U .
(2)
Выпуклая функция может не быть дифференцируемой даже во внутренних точках
области определения. Для таких функций неравенство (1)
I (u ) ³ I (v) + c(v), u - v , (1)
является обобщением неравенства (2).
Из сказанного выше следует, что субдифференциал гладких выпуклых функций не пуст,
а градиенты этих функций суть их субградиенты. Следующая теорема утверждает, что во
внутренних точках области определения гладкая выпуклая функция других субградиентов
иметь не может.
Теорема 1.
: U R1 ,
I Î C 1 ( U ) , то
Пусть функция I
выпукла. Тогда если
Доказательство.
где U
Rn
выпуклое множество,
¶I (v ) = { I '(v)} "v Î int U .
Вложение
{ I ' (v)} ¶I (v), "v Î int U
следует непосредственно из неравенства (2). Докажем обратное вложение.
Пусть
5.
c ( v ) Î ¶I ( v ) .I Î C 1 (U )
В силу
для любых
u ÎU
справедливо равенство
I (u ) = I (v) + I '(v), u - v + O ( u - v ) .
-
I (u ) ³ I (v) + c (v), u - v (1)
0 £ I '(vс) -v (u), v - O+ u( v -
I '(vс) -v (u), v - O³ u( v Условие v Î int U влечет за собой включение
для всех достаточно малых
u( e )
e > 0.
)
).
>0
мало
u(e ) = v- e
В неравенстве (3) полагаем
Þ
(3)
( I '(vс) -v ( )U
)Î
u = u ( e ) . Имеем
= I '(vс) -v ( ), v -Ie ( '(v) - с(v ) ) - v =
I '(vс) -v ( u), v -
= -e I '(vс) -v ( I ), v '( с) -v
2
-e I '(vс) -v ( ) O³
(e) Þ
( )
= -e I '(vс) -v ( )
2
O( e )
I '(vс) -v ( ) £
Þ
e
Þ
I '(vс) -v ( ) = 0 Þ I '(vс) =v ( ) Þ с(v) Î { I '(v)} .
Теорема доказана.
6.
Пример 1. Пусть g : Rn
R1 произвольная функция и g ( v ) = 0.
I (u) = g(u) , u Î R n
Тогда для функции
0 Î ¶I ( v ) . Действительно, для всех u Î R n имеем
I ( u)
I ( v)
g( v)
0, u - v
}
}
}
}
g ( u ) ³ 0 Þ g ( u ) ³ g ( v ) Þ I (u ) ³ I (v) + 0 Þ
справедливо включение
Þ I (u ) ³ I (v) + 0, u - v .
Полученное неравенство в силу (1)
c(v) Î ¶I ( v ) Û I (u ) ³ I (v) + c(v), u - v (1)
и означает, что
c ( v ) = 0 Î ¶I ( v ) .
Существуют не дифференцируемые в точке функции, субдифференциал которых не пуст.
Пример 2. Функция
в точке
v=0
I : R n R1 , определенная равенством I (u ) = u , u Î R n ,
не дифференцируема, но в силу предыдущего примера
Более того, для этой функции из неравенства
c £1
c, u £ c × u
справедливо
¶I (0) ¹ Æ.
следует, что при
³ c ,u
6
78
I (0)
I (u ) = 0 + 1 × u ³ I (0) + c × u ³ I (0) + c, u = I (0) + c, u - 0 Þ
³с
I (u ) ³ I (0) + c, u - 0 ,
c £ 1.
7.
ПоследнееI (u ) ³ I (0) + c, u - 0 ,
Таким образом, справедливо вложение
{
c Î Rn
c £1
означает, что
c Î ¶I ( 0 ) .
}
c £ 1 ¶I (0).
Упражнение. Доказать, что в разобранном примере на самом деле имеет место равенство
{
}
c Î Rn
c £ 1 = ¶I (0).
Решение.
В силу (1) достаточно доказать, что для любого c Î R
такой, что
uˆ
0
I (uˆ ) < I (v)+
В качестве такого полагаем
uˆ =
c >1
n
,
c >1
=0
c , uˆ - v Þ uˆ < c, uˆ .
с
Þ uˆ = 1.
с
с
c, uˆ = cс,
с
Требуемое неравенство имеет место.
Тогда
2
с
=u =
с
>1= ˆ .
найдется
uˆ Î R n ,
8.
Пусть функцияæ u1 ö
ç ÷
u = ç L ÷ Î Rn.
ç un ÷
è ø
I : R n R1
Обозначим
В частности, пусть
Заметим, что
определена формулой
{
iÎ{ 1,L , n}
}
Z ( v ) = i Î { 1,L , n} v i = max v s .
æ2ö
ç ÷
0÷
ç
n = 4, v =
.
ç2÷
ç ÷
è -1ø
для всех
I ( u ) = max u i ,
v Î Rn
sÎ{ 1,L , n}
Тогда
I ( v ) = 2, Z ( v ) = { 1,3} .
имеет место равенство
I ( v ) = vi , i Î Z ( v ) .
( 4)
Для частного случая
I ( v ) = v1 = v 3 = 2, Z ( v ) = { 1,3} .
9.
Упражнение. Доказать, что функцияРешение.
Тогда
Пусть
I ( u ) = max u i
iÎ{ 1,L , n}
u1 , u2 Î R n , a Î [ 0,1] .
Полагаем
является выпуклой.
ua = a u1 + ( 1 - a ) u2 .
i
i
I ( ua ) = max ( uai ) = max ( a u1 + ( 1 - a ) u2 ) £
iÎ{ 1,L , n}
iÎ{ 1,L , n}
)
æ 64 I7( u1 )48
ö
6 4I7( u2 48
£ çç a max ( u1i ) + ( 1 - a ) max ( u2i ) ÷÷ = a I ( u1 ) + ( 1 - a ) I ( u2 ) .
iÎ 1,L , n
iÎ{ 1,L , n}
ç { }
÷
è
ø
Выпуклость функции I доказана.
Пример 3. Доказать, что для всех
v Î Rn
справедливо
ì æ c1 ö
ü
ï ç ÷
ï
¶I ( v ) = íc = çL ÷ c1 + L + cn = 1, ci ³ 0, i = 1,L , n; ci = 0, i Ï Z ( v ) ; ý . ( 5 )
ï çc ÷
ï
î è nø
þ
æ0ö
ç ÷
çL ÷
В частности, если Z ( v ) = { i* } , то ¶I ( v ) = ç 1 ÷ , где 1 стоит на i* месте.
ç ÷
çL ÷
ç0÷
è ø
10.
Решение.Правую часть равенства (5)
ì æ c1 ö
ü
ï ç ÷
ï
¶I ( v ) = íc = çL ÷ c1 + L + cn = 1, ci ³ 0, i = 1,L , n; ci = 0, i Ï Z ( v ) ;ý .
ï çc ÷
ï
î è nø
þ
обозначим символом
Пусть
следует, что
c Î A( v) .
max u j
jÎ{ 1,L ,n}
A( v) .
Требуется доказать, что
Покажем, что
A ( v ) = ¶I ( v ) .
c Î ¶I ( v ) . Из (4) I ( v ) = vi , i Î Z ( v ) ( 4 )
vi , iÎZ ( v )
æ
u j ö÷ - v i , u , v Î R n , i Î Z ( v ) .
I ( u ) - I ( v ) = ç jÎmax
è { 1,L ,n} ø
Каждое из равенств в (6) умножим на
( I ( u) - I ( v) ) å c
iÎZ ( v )
i
i
( 5)
ci
и сложим их по всем
i Î Z ( v ) . Имеем
= æç max u j ö÷ å ci - å ci v i =
è jÎ{ 1,L , n} ø iÎZ ( v )
iÎZ ( v )
,u - v
6 44c7
4 48
³u
6 47
48
n
n
n
n
³0
æ
j ö
i
i
= å ç max u ÷ ci - å ci v ³å u ci - å ci v i =
jÎ{ 1,L , n}
ø
i =1 è
i =1
i =1
i =1
n
i
i
c
u
v
)=
å i(
i =1
(6)
11.
,u - v6 44c7
4 48
n
= å ci ( u i - v i ) = c, u - v .
i =1
n
Заметим, что
1 = å ci
ci = 0, iÏZ ( v )
}
=
i =1
å c.
iÎZ ( v )
i
Тогда
=1
678
( I ( u ) - I ( v ) ) å ci ³ c, u - v Þ I ( u ) - I ( v ) ³ c, u - v Þ
iÎZ ( v )
I ( u ) ³ I ( v ) + c, u - v Þ c Î ¶I ( v ) .
c(v) Î ¶I ( v ) Û I (u ) ³ I (v) + c(v), u - v (1)
Из доказанного включения
c Î ¶I ( v )
Докажем обратное вложение
¶I ( v ) A ( v ) .
Пусть
c Î ¶I ( v ) .
следует, что
A ( v ) ¶I ( v ) .
Тогда по определению субградиента
c
12.
c(v) Î ¶I ( v ) Û I (u ) ³ I (v) + c(v), u - v (1)получим
æ
jö
max
u
ç
÷
è jÎ{ 1,L ,n} ø
æ
jö
max
v
ç
÷
è jÎ{ 1,L ,n} ø
I ( u ) - I ( v ) ³ c, u - v , u Î R n Þ
æ max u j ö - æ max v j ö ³ c, u - v , u Î R n
ç jÎ{ 1,L ,n} ÷ ç jÎ{ 1,L ,n} ÷
è
ø è
ø
Обозначим
æ v1 ± 1 ö
ç
÷
u± = ç L ÷ .
ç v n ± 1÷
è
ø
В (7) полагаем
u = u± .
(7)
Последовательно вычисляем
левую и правую части (7)
æ max v j ± 1 ö - æ max v j ö =
)
ç jÎ{ 1,L ,n} (
÷ ç jÎ{ 1,L , n} ÷
è
ø è
ø
±1.
n
n
c, u± - v =
åc ( v
i =1
i
i
± 1 - v ) = ± å ci .
i
i =1
Þ
n
±1 ³ ± å ci Þ
i =1
13.
n±1 ³ ± å ci Þ
i =1
ì n
ï å ci £ 1
ï i =1
Þ
í n
ï - c £ -1
å
i
ï
î i =1
ì æ c1 ö ci ³ 0, i Î { 1,L , n} ;
ï ç ÷
A ( v ) = íc = çL ÷ ci = 0, i Ï Z ( v ) ;
ï ç c ÷ c +L + c = 1
1
n
î è nø
Для
e >0
и всех
I ( ue-i ) £ I ( v ) .
i Î { 1,L , n}
n
åc
i =1
ü
ï
ý
ï
þ
полагаем
По определению субградиента
I ( u ) - I ( v ) ³ c, u - v (7)
( 7)
при
u = ue-i
i
= 1.
( 8)
æ v1 ö
ç
÷
ç L ÷
ue-i = ç vi - e ÷ . Очевидно, что
ç
÷
ç L ÷
c
ç v n ÷ в силу (7)
è
ø
имеем
0 ³ I ( ue-i ) - I ( v ) ³ c, ue i - v =
n
-j
j
c
u
v
å j ( ei ) =
j =1
14.
n0 ³ å c j ( ue-i j - v j )
0
= å c j ( v j - v j ) + ci ( v i - e - v i ) =
n
j =1
j ¹i
j =1
= ci ( -e ) Þ 0 ³ ci ( -e ) Þ
ì æ c1 ö ci ³ 0, i Î { 1,L , n} ;
ï ç ÷
A ( v ) = íc = çL ÷ ci = 0, i Ï Z ( v ) ;
ï ç c ÷ c +L + c = 1
1
n
î è nø
Полагаем
æ v1 ö
ç
÷
L
ç
÷
ç <I ( v) ÷
+
ue i = ç i
v +e ÷
ç
÷
ç L ÷
ç vn ÷
è
ø
ci ³ 0, i Î { 1,L , n} .
ü
ï Далее пусть
ý
ï
þ
Очевидно, что
i Ï Z ( v ) Þv i < I ( v ) Þ
$e > 0 : v i + e < I ( v ) .
I ( ue+i ) = I ( v ) .
В силу (7) I ( u ) - I ( v ) ³ c, u - v ,
при
u = ue+i
( 9)
u Î Rn
имеем
0= I(u
+
ei
( 7)
) - I ( v) ³
= åc ( u
n
j =1
³0
j
+j
ei
³0
c , ue+i - v =
-vj) =
(7)
15.
n³
= å c j ( ue+i j - v j ) =
j =1
n
n
+j
c
u
å j ei
j =1
j ¹i
0
e
æ}
ö
+ ci ç ue+ii - v i ÷ =
ç
÷
è
ø
³0
vi + e
= å c j ( v j - v j ) + ci ( v i + e - vi ) = e ci £ 0 Þ ci £ 0, i Ï Z ( v ) .
j =1
j ¹i
Отсюда и (9)
ci ³ 0, i Î { 1,L , n} .
( 9)
выводим
ci £ 0, ci ³ 0 Þ ci = 0, i Ï Z ( v ) .
Тогда
c Î A( v) .
Таким образом,
ì æ c1 ö ci ³ 0, i Î Z ( v ) ;
ï ç ÷
A ( v ) = íc = çL ÷ ci = 0, i Ï Z ( v ) ;
ï ç c ÷ c +L + c = 1
n
î è nø 1
ü
ï
ý
ï
þ
¶I ( v ) A ( v ) Þ ¶I ( v ) = A ( v ) .
16.
Упражнение.Для частного случая
æ2ö
ç ÷
0÷
ç
n = 4, v =
ç2÷
ç ÷
è -1ø
доказать, что
ì æ c1 ö
ü
ï ç ÷
ï
ï ç0÷
ï
c Î A ( v ) = íc =
c1 + c3 = 1, c1 ³ 0, c3 ³ 0 ý Þ c Î ¶I ( v )
ï ç c3 ÷
ï
ç
÷
ï è0ø
ï
î
þ
4
Решение. Требуется доказать, что c Î ¶I ( v ) . Для любого c Î A ( v ) и u Î R
имеем
max u j
c1 + c3
c1 + c3
}
}2
}
}
æ
j ö
I ( u ) - I ( v ) = 1 × ç max u ÷ - 1 × 2 = ( c1 + c3 ) æç max u j ö÷ - 2 ( c1 + c3 ) =
è jÎ{ 1,L ,4} ø
è jÎ{ 1,L ,4} ø
jÎ{ 1,L ,4}
³u
³u
æ 64 7
48 ö ³0 æ 64 7
48 ö
³0
= c1 × ç max u j ÷ + c3 × ç max u j ÷ - 2c1 - 2c3 ³ c1u1 + c3u3 - 2c1 - 2c3 =
ç jÎ{ 1,L ,4} ÷
ç jÎ{ 1,L ,4} ÷
è
ø
è
ø
1
3
17.
= c1u1 + c3u3 - 2c1 - 2c3 =v4
v3
v1
v2
æ
ö
æ
ö
æ
ö
æ
ö
= c1 ç u1 - 2 ÷ + 0 × ç u2 - 0 ÷ + c3 ç u3 - 2 ÷ + 0 × ç u4 - ( -1) ÷ =
è
ø
è
ø
è
ø
è
ø
4
= å ci ( u i - vi ) = c, u - v Þ
i =1
I ( u ) - I ( v ) ³ c, u - v Þ
I ( u ) ³ I ( v ) + c, u - v Þ c Î ¶I ( v ) .
Утверждение доказано.
18.
Упражнение.Для частного случая
æ2ö
ç ÷
0÷
ç
n = 4, v =
ç2÷
ç ÷
è -1ø
доказать, что
ì æ c1 ö
ü
ï ç ÷
ï
ï ç0÷
ï
c
Î
A
v
=
c
=
c
+
c
=
1,
c
³
0,
c
³
0
c Î ¶I ( v ) Þ
( ) í ç ÷ 1 3
ý.
1
3
c3
ï
ï
ç
÷
ï è0ø
ï
î
þ
Решение.
æ
jö
ç max u ÷
è jÎ{ 1,L ,4} ø
}
}2
c Î ¶I ( v ) Û I ( u ) ³ I ( v ) + c, u - v Þ
æ max u j ö ³ 2 + c × u1 - 2 + c u 2 - 0 +
) 2(
)
ç jÎ{ 1,L ,4} ÷
1 (
è
ø
+c3 × ( u 3 - 2 ) + c4 × ( u 4 - ( -1) ) , "u Î R 4
( 11)
19.
Обозначим:Подставим u+
æ 3ö
æ 2 ±1 ö
ç ÷
ç
÷
1÷
0
±
1
ç
ç
÷
,
u± =
Þ u+ =
ç 3÷
ç 2 ±1 ÷
ç ÷
ç
÷
1
±
1
è0ø
è
ø
æ 1ö
ç ÷
-1 ÷
ç
u- =
.
ç 1÷
ç ÷
è -2 ø
6 4 73 4 8
æ 31 ö
æ 12 ö
æ 33 ö
æ 04 ö
j ö
æ
в (11) ç max u ÷ ³ 2 + c1 × ç u - 2 ÷ + c2 ç u - 0 ÷ + c3 × ç u - 2 ÷ + c4 × ç u + 1÷
è jÎ{ 1,L ,4} ø
è
ø
è
ø
è
ø
è
ø
( 11)
3 ³ 2 + c1 × ( 3 - 2 ) + c2 + c3 × ( 3 - 2 ) + c4 × ( 0 + 1) Þ
Подставим
u-
c1 + c2 + c3 + c4 £ 1.
( 12 )
6 47 48
1
-1
1
-2
в (11) æç max u j ö÷ ³ 2 + c × æ u1 - 2 ö + c æ u 2 - 0 ö + c × æ u 3 - 2 ö + c × æ u 4 + 1ö
1 ç
÷ 2ç
÷ 3 ç
÷ 4 ç
÷
è jÎ{ 1,L ,4} ø
è
ø
è
ø
è
ø
è
ø
1
1 ³ 2 + c1 × ( 1 - 2 ) + ( -1) u 2 + c3 × ( 1 - 2 ) + c4 × ( -2 + 1) Þ
-1 ³ -c1 - c2 - c3 - c4 Þ c1 + c2 + c3 + c ³ 1
Из (12) и (13) следует
c1 + c2 + c3 + c4 = 1.
( 14 )
( 13)
( 11)
20.
Полагаемæ2-e ö
æ 2 ö
æ 2 ö
æ 2 ö
ç
÷
ç
÷
ç
÷
ç
÷
0
0
e
0
0
÷ , u- = ç
÷ , u- = ç
÷ , u- = ç
÷
ue-1 = ç
ç 2 ÷ e2 ç 2 ÷ e3 ç2 -e ÷ e4 ç 2 ÷
ç
÷
ç
÷
ç
÷
ç
÷
è -1 ø
è -1 ø
è -1 ø
è -1 - e ø
Последовательно подставляем в (11)
æ max u j ö ³ 2 + c × u1 - 2 + c u 2 + c × u 3 - 2 + c × u 4 + 1
) 2 3(
) 4(
)
ç jÎ{ 1,L ,4} ÷
1 (
è
ø
( 11)
u = ue-1 Þ 2 ³ 2 + c1 × ( -e ) Þ c1 ³ 0
u = ue-2 Þ 2 ³ 2 + c2 ( -e ) Þ c2 ³ 0
u = ue-3 Þ 2 ³ 2 + c3 ( -e ) Þ c3 ³ 0
u = ue-4 Þ 2 ³ 2 + c4 ( -e ) Þ c4 ³ 0
c1 ³ 0, c2 ³ 0, c3 ³ 0, c4 ³ 0.
Þ
21.
æ 2 öæ 2 ö
ç <2 ÷
ç
÷
0
ç0+e ÷ + ç
÷
+
,
u
=
Полагаем ue 2 =
ç
÷ e 4 ç 2 ÷ . Последовательно подставляем в (11)
ç 2 ÷
ç <2 ÷
ç -1 ÷
ç -1 + e ÷
è
ø
è
ø
æ max u j ö ³ 2 + c × u1 - 2 + c u 2 + c × u 3 - 2 + c × u 4 + 1 , 11
( )
)
)
)
ç jÎ{ 1,L ,4} ÷
1 (
2
3 (
4 (
è
ø
u = ue+2 Þ 2 ³ 2 + c2 × e Þ c 2 £ 0, c 2 ³ 0 Þ c 2 = 0
u = ue+4 Þ 2 ³ 2 + c4 × ( e ) Þ c 4 £ 0, c 4 ³ 0 Þ c 4 = 0.
Утверждение доказано.
Таким образом, для частного случая доказано
ì æ c1 ö
ü
ï ç ÷
ï
ï ç0÷
ï
¶I ( v ) = íc =
c1 + c3 = 1, c1 ³ 0, c3 ³ 0 ý .
ï ç c3 ÷
ï
ç
÷
ï è0ø
ï
î
þ
22.
ìïæ u1 ö üïУпражнение. Для функции I ( u ) = max íç 2 ÷ ý найти ее субдифференциал
ïîè u ø ïþ
æ1ö
æ 2ö
æ1ö
в точках v1 = ç ÷ , v2 = ç ÷ , v3 = ç ÷ . Построить эти множества на плоскости c1Oc2 .
è1ø
è1ø
è 2ø
Решение.
ìï æ c1 ö
üï
¶I ( v ) = íc = ç ÷ c1 + c2 = 1, c1 ³ 0, c2 ³ 0; ci = 0, i Ï Z ( v ) ý
ïî è c2 ø
ïþ
{
}
Z ( v ) = i Î { 1, 2} v i = max v s .
Z ( v1 ) = { 1, 2} Þ
sÎ{ 1,2}
ìï æ c1 ö
üï
¶I ( v1 ) = íc = ç ÷ c1 + c2 = 1, c1 ³ 0, c2 ³ 0 ý
ïî è c2 ø
ïþ
ìæ 1 ö ü
Z ( v2 ) = { 1} Þ ¶I ( v2 ) = íç ÷ ý
îè 0 ø þ
Z ( v3 ) = { 2} Þ ¶I ( v ) = ìíæ 0 ö üý
3
ç ÷
îè 1 ø þ
¶I ( v3 )
c1
¶I ( v1 )
¶I ( v2 )
c1
















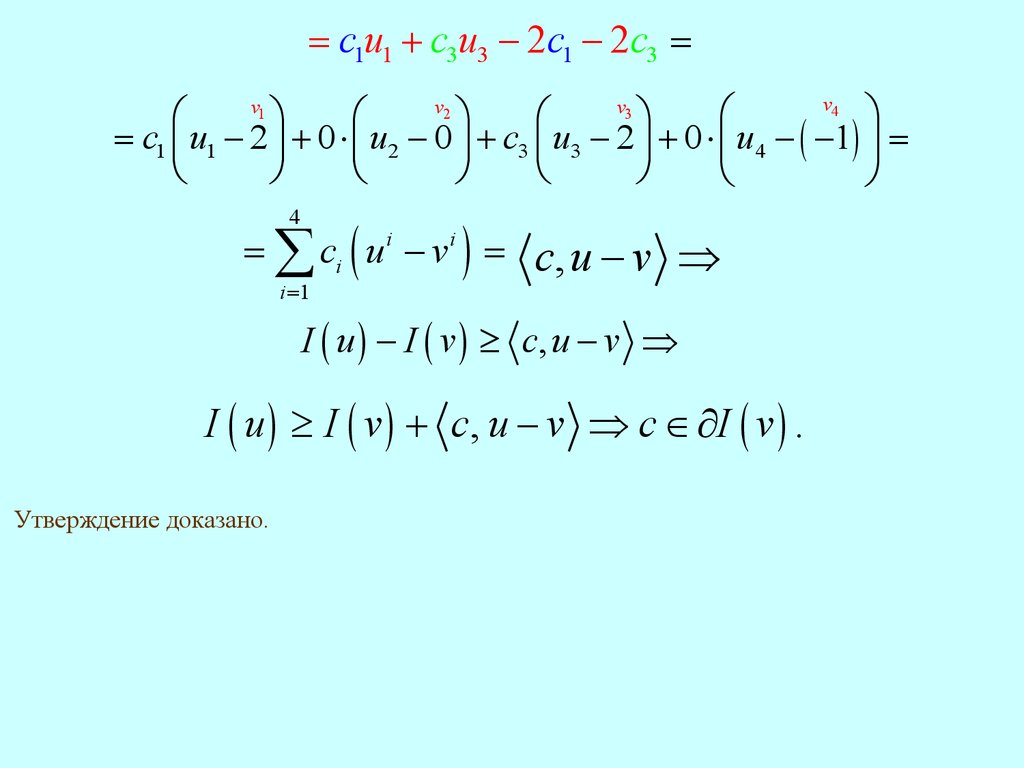






 Математика
Математика Программирование
Программирование








