Похожие презентации:
Выпуклый анализ. Связь между выпуклыми функциями и выпуклыми множествами. Лекция 15
1. ВЫПУКЛЫЙ АНАЛИЗ
ЛЕКЦИЯ 154. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИ И
ВЫПУКЛЫМИ МНОЖЕСТВАМИ
2.
4. СВЯЗЬ МЕЖДУ ВЫПУКЛЫМИ ФУНКЦИЯМИИ ВЫПУКЛЫМИ МНОЖЕСТВАМИ
(ПРОДОЛЖЕНИЕ)
4.3. Опорная функция подмножества пространства
(продолжение)
Rn .
4.4. Опорные функции выпуклых оболочек подмножеств
пространства
Rn .
3.
4.3. Опорная функция подмножества пространстваСвойство 7.
Пусть
U ,U 0 R
n
Rn .
(продолжение)
компактные множества и
v, v0 Î R n .
Тогда
cU ( v ) - cU 0 ( v0 ) £ v0 r ( U ,U 0 ) + U 0 v - v0 + 2 r ( U ,U 0 ) v - v0 ,
где
r ( U , U 0 ) = min { R ³ 0 U U 0 + O ( 0, R ) , U 0 U + O ( 0, R ) } -
расстояние Хаусдорфа между множествами U и
U 0 = max u uÎU 0
модуль
Доказательство. Из свойства 2
следует
множества
U0;
U0.
cU ( v1 + v2 ) £ cU ( v1 ) + cU ( v2 )
cU ( v ) = cU ( v - v0 + v0 ) £
cU ( v - v0 ) + cU ( v0 ) Þ
cU ( v ) £ cU ( v - v0 ) + cU ( v0 ) .
Оценим каждое из слагаемых в правой части (3).
опорных функций
( 3)
4.
Из вложенияU O ( 0, U
)
по свойству 6 следует неравенство
шар:= U × v - v0
U
6 44 7 4 48
cU ( v - v0 ) £ c O( 0, U ) ( v - v0 ) = U v - v0 Þ
cU ( v - v0 ) £ U v - v0 .
( 4)
O ( 0, U
)
U
По определению расстояния Хаусдорфа выводим
U U0 (
r U ,U 0 )
Тогда
cU ( v0 )
свойство 4
=
= U 0 + O ( 0, r ( U , U 0 ) ) .
свойство 6
£
cU 0 +O( 0, r ( U ,U 0 ) ) ( v0 )
= r ( U ,U 0 ) v0
6 4 4 7 4 48
cU0 ( v0 ) + c O( 0, r ( U ,U ) ) ( v0 ) =
0
свойство 4
=
cU 0 ( v0 ) + r ( U , U 0 ) v0 Þ
cU ( v0 ) £ cU 0 ( v0 ) + r ( U ,U 0 ) v0 .
( 5)
5.
Подставим полученные неравенства (4) и (5) в (3).( 4 ) Þ£ U
v - v0
cU ( v ) £ cU ( v - v0 ) +
( 5) Þ£ cU 0 ( v0 ) + r ( U ,U 0 )
cU ( v0 )
v0
( 3) Þ
cU ( v ) £ U v - v0 + cU 0 ( v0 ) + r ( U ,U 0 ) v0
cU ( v ) - cU 0 ( v0 ) £ U v - v0 + r ( U ,U 0 ) v0 .
Меняя местами
U ,U 0 R n
и
v, v0 Î R n ,
Þ
( 6)
получим
cU0 ( v0 ) - cU ( v ) £ U 0 v0 - v + r ( U 0 ,U ) v .
Из (6) и (7) в силу очевидного равенства
x = max { - x, x} "x Î R1
( 7)
выводим
cU ( v ) - cU 0 ( v0 ) =
U v - v0 + r ( U ,U 0 ) v0 ( 6 ) £ U 0 v0 - v + r ( U 0 ,U ) v ( 7 )
ì£ 6
4 47 4 48
6 4 47 4 48 ü
ï
ï
= max í cU ( v ) - cU 0 ( v0 ) , cU 0 ( v0 ) - cU ( v ) ý £
ï
ï
î
þ
6.
U v - v0 + r ( U ,U 0 ) v0 ( 6 ) £ U 0 v0 - v + r ( U 0 ,U ) v ( 7 )ì£ 6
4 47 4 48
6 4 47 4 48 ü
ï
ï
= max í cU ( v ) - cU 0 ( v0 ) , cU 0 ( v0 ) - cU ( v ) ý £
ïî
ïþ
£ max { U v - v0 + r ( U , U 0 ) v0 ,
U 0 v0 - v + r ( U 0 , U ) v } £
£ max { U v - v0 , U 0 v0 - v } + max { r ( U ,U 0 ) v0 , r ( U 0 , U ) v } =
= v - v0 max { U , U 0 } + r ( U ,U 0 ) max { v0 , v } Þ
cU ( v ) - cU 0 ( v0 ) £
£ v - v0 max { U , U 0 } + r ( U ,U 0 ) max { v0 , v } .
Заметим, что
U = r ( U , { 0} )
( 8)
U0
6 47
48
£ r ( U ,U 0 ) + r ( U 0 , { 0} ) = r ( U , U 0 ) + U 0 Þ
ì£ r ( U},U 0 ) + U0
ï
max í U
, U0
ïî
ü
ï
ý £ r ( U ,U 0 ) + U 0 .
ïþ
U
( 9)
O ( 0, U
)
U
7.
v = v - v0 + v0 £v - v0 + v0 Þ
£ v - v0 + v0
ì
ü
}
ï
ï
max í v0 , v ý £ v - v0 + v0 ,
ïî
ïþ
Подставим (9) max { U , U 0 } £ r ( U , U 0 ) + U 0
( 8) :
cU ( v ) - cU 0 ( v0 )
( 9)
( 10 )
и (10) в (8)
£ r ( U ,U 0 ) + U 0 ( 9 )
6 44 7 4 48
£ v - v0 × max { U , U 0 } +
64 7 48( 10)
max { v0 , v } £
£ v - v0 + v0 ,
+ r ( U ,U 0 )
£ v - v0
( r ( U ,U ) + U ) + r ( U ,U ) (
0
0
0
v - v0 + v0 ) =
= v - v0 × r ( U ,U 0 ) + v - v0 × U 0 + r ( U , U 0 ) × v - v0 + r ( U ,U 0 ) × v0 =
= v0 r ( U , U 0 ) + U 0 v - v0 + 2 r ( U ,U 0 ) v - v0 ,
что и требовалось доказать.
cU ( v ) - cU 0 ( v0 ) £ v0 r ( U ,U 0 ) + U 0 v - v0 + 2 r ( U ,U 0 ) v - v0
8.
Следствие.cU ( v )
Опорная функция
v Î Rn , U Rn
непрерывна по совокупности переменных
и, следовательно, по каждому из них в отдельности.
4.4. Опорные функции выпуклых оболочек подмножеств пространства
Пусть
Rn .
U R n компактное множество. Ранее было доказано, что множество
также компактно.
Установим некоторые свойства опорных функций выпуклых
оболочек компактных подмножеств пространства
Свойство 1.
Пусть
U Rn
Rn .
компактное множество. Тогда
cU ( v ) = c coU ( v ) , "v Î R n .
Доказательство.
Из вложения
U co U
следует
cU ( v ) £ c coU ( v ) , "v Î R n .
Докажем неравенство в другую сторону.
Имеем
( 1)
coU
9.
u=n+1
å l iui ,ui ÎU ,li ³0,
i =1
n+1
å
i =1
=
i =1,L , n +1,
c coU ( v ) = max u , v
uÎcoU
li =1
=
max
li ³ 0,ui ÎU ,
i =1,L , n +1,
n+1
å li =1
ui ÎU ,li ³ 0,
ål
i =1
i
n +1
å li =1
i =1
i i
=
i =1
n+1
n +1
ål u , v
max
i =1,L , n +1,
u, v
å li max
uÎU
=1
6 i4
748
£
n +1
U ( v)
æ n +1 64c7
48
max ç å l i max u , v
li ³ 0,i =1,L , n +1 ç
uÎU
ç i =1
n+1
å l i =1, è
ui , v £
ö
÷=
÷÷
ø
i =1
æ }1 ö
n +1
n +1
ç
÷ cU ( v ) Þ
æ
ö c v
= max ç å l i cU ( v ) ÷ = U ( ) n+1 max ç å l i ÷ =
li ³ 0,i =1,L , n +1
i =1
è i =1
ø
n +1
å l i =1,
ç
÷
i =1
l
=
1,
è
ø
å i
li ³ 0,i =1,L , n +1
i =1
i =1
Из (1)
c coU ( v ) £ cU ( v ) , "v Î R n .
cU ( v ) £ c coU ( v ) , "v Î R n
свойства.
( 1)
( 2)
и (2) следует справедливость доказываемого
10.
Упражнение. Найти опорную функцию множестваìïæ x ö
üï
U = íç ÷ 2 x + y £ 2, x ³ 0, y ³ 0 ý
ïîè y ø
ïþ
y
æ 3ö
и вычислить ее в точке v* = ç ÷ .
è 2ø
Решение.
A ( 0, 2 )
ìæ 0 ö æ 1 ö æ 0 ö ü
ì
0
1
0
ü
æ
ö
æ
ö
æ
ö
%
U%= íç ÷ , ç ÷ , ç ÷ ý , U = coU = co íç ÷ , ç ÷ , ç ÷ ý
îè 0 ø è 0 ø è 2 ø þ
îè 0 ø è 0 ø è 2 ø þ
Для всех
U
O ( 0, 0 ) B ( 1, 0 )
v Î R2
имеем
cU ( v ) = cU%( v ) = max
v, u =
%
uÎU
ìï æ v1 ö æ 0 ö æ v1 ö æ 1 ö æ v1 ö æ 0 ö
x = max í ç ÷ , ç ÷ , ç ÷ , ç ÷ , ç ÷ ç ÷
ïî è v2 ø è 0 ø è v2 ø è 0 ø è v2 ø è 2 ø
= max { 0, v1 , 2v2 } ,
cU ( v* ) = max { 0,3, 2 × 2} = 4.
üï
ý=
ïþ





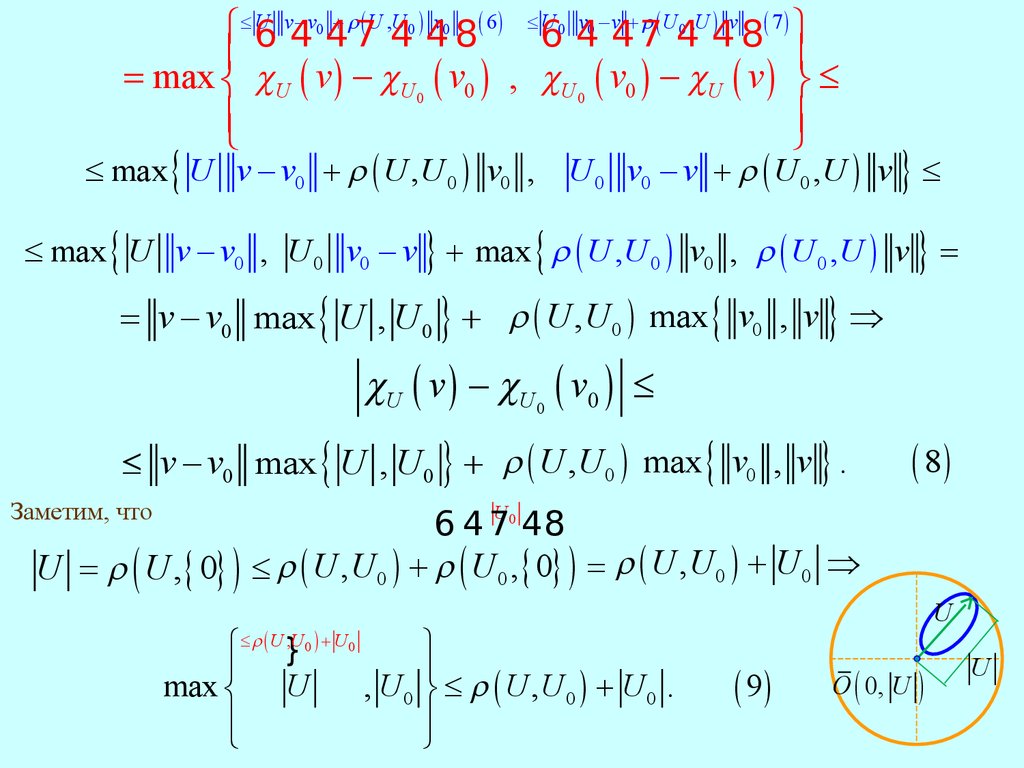





 Математика
Математика Программирование
Программирование








