Похожие презентации:
Многочлены и рациональные функции
1.
§3. Многочлены ирациональные функции
п.1. Многочлены.
Рассмотрим уравнения:
ax b 0 — линейное уравнение
— многочлен 1-й степени
ax bx c 0 — квадратное уравнение
2
— многочлен 2-й степени
2.
ax bx cx d 0 — кубическое уравнение3
3
— многочлен 3-й степени
Пример 1.
x 4 x 5x 0;
3
2
x 4 x 3x 12 0;
3
x x 1 0.
3
2
Формулы Кардано для решение кубических
уравнений.
Метод Феррари для решение уравнений 4-й
степени.
Общее уравнение степени не ниже 5 не
разрешимо в радикалах.
3.
Выражение видаan x an 1 x
n
n 1
... a1 x a0 ,
где ak R, k 0, n, an 0, называется
многочленом n-й степени.
Обозначается:
Число
если
Pn (x).
x0 называется корнем многочлена Pn (x),
Pn ( x0 ) 0.
4.
Теорема 1 (о делении с остатком).Пусть
f ( x), g ( x) — некоторые многочлены;
g ( x) 0.
Тогда существуют многочлены q( x), r ( x) такие,
что
f ( x) g ( x) q( x) r ( x),
причем степень многочлена r (x) меньше
степени многочлена g (x).
5.
Пример 2.f ( x) 2 x x 3x x 4 x 2;
2
g ( x) x 2 x 3.
Найти q( x), r ( x).
5
4
3
Решение.
Разделим в столбик.
2
6.
x2
x
3
2 x x 4 3x
x
4
x
2
3
2x 4x 6x
3
2
4
3
2
2
x
3
x
9
x
26
3x 3x x 4 x 2
4
3
2
q(x)
3x 6 x 9 x
3
2
9 x3 8 x 2 4 x 2
9 x 18 x 27 x
2
26 x 2 23x 2
26 x 52 x 78
75x 76 r (x)
5
5
4
3
2
2
Значит,
2 x x 3x x 4 x 2
2
3
2
( x 2 x 3)(2 x 3x 9 x 26) (75x 76)
5
4
3
2
7.
Теорема 2 (Безу).Остаток от деления многочлена P (x ) на
двучлен ( x a ) равен значению P (x ) при
Пример.
P( x) x 2 x 3x 5;
a 1.
r 7 P(1).
3
2
x a.
8.
Доказательство.Пусть r (x) — остаток от деления
( x a).
P (x) на
По теореме 1 степень многочлена r (x)
меньше степени многочлена ( x a ), т.е. равна
нулю.
Значит, r (x) — число, т.е.
По теореме 1
r ( x ) r.
P ( x ) ( x a ) q ( x ) r.
Положим x a :
P(a) (a a) q(a) r r P(a).
9.
Следствие.Число x a является корнем многочлена P (x )
тогда и только тогда, когда остаток от
деления P (x ) на ( x a ) равен нулю.
Доказательство.
Необходимость.
Пусть x a — корень многочлена P (x ), т.е.
P(a) 0.
Тогда по теореме 2, остаток равен
r P(a) 0.
Достаточность.
Если r 0, то по теореме 2 P(a) r 0,
т.е. x a — корень многочлена P (x ).
10.
Таким образом, если известен один изкорней x a уравнения P( x) 0,
то степень уравнения можно понизить на 1,
разделив P (x ) на ( x a).
Пример. Решить уравнение
x 2 x 3x 2 0.
Решение. Очевидно, x 1 — корень
3
2
уравнения.
3
2
Разделив x 2 x
3x 2 на x 1, получим
2
x x 2.
Значит,
x 2 x 3x 2 ( x 1)( x x 2).
3
2
2
11.
Схема ГорнераДеление многочлена на двучлен, удобно
выполнять по следующей схеме.
Пусть в результате деления многочлена
n 1
an x an 1 x ... a1 x a0
на двучлен x a в частном получается
n
многочлен
bn 1 x
n 1
и в остатке r.
Тогда
an 2 x
n 2
... b1 x b0
12.
aan
bn 1 an
... a1
a0
bn 2 abn 1 an 1 ... b ab a r ab0 a0
an 1
0
1
1
Пример. Разделить x x 6 x 14 x 11x 3
на x 3.
5
3
4
3
1
1
–6
– 14
1
4
6
4
2
– 11
1
–3
0
Значит,
x x 6 x 14 x 11x 3 ( x 3)( x 4 x 6 x 4 x 1)
5
4
3
2
4
3
2
13.
Теорема 3 (основная теоремы алгебры).Всякий многочлен n-й степени ( n 0 ) имеет по
крайней мере один корень (действительный
или комплексный).
k
Если многочлен P (x ) делится на ( x a) , то
число x a называется корнем кратности k
этого многочлена.
Пусть P (x ) — многочлен с действительными
коэффициентами.
Если
то и
P(a ib ) 0,
P(a ib ) 0.
14.
Следствие (основной теоремы алгебры).Всякий многочлен n-й степени ( n 0 ) имеет
равно n корней (действительных или
комплексных) с учетом их кратности.
Всякий многочлен Pn (x) с действительными
коэффициентами n-й степени разлагается на
линейные и квадратные множители с
действительными коэффициентами, т.е.
Pn ( x) a0 ( x x1 ) ( x x2 ) ...( x xr )
sm
s1
2
2
( x p1 x q1 ) ...( x pm x qm ) ,
где k1 ... kr s1 ... sm n и
2
pi 4qi 0, i 1, m.
k1
k2
kr
15.
Рациональные корни многочленаТеорема 4.
Пусть
n 1
Pn ( x) an x an 1 x ... a1 x a0 ,
где ak Z, k 0, n, an 0.
n
Если несократимая дробь
p
, p, q Z,
q
является корнем этого многочлена, то
p — делитель a0 ,
q — делитель an .
16.
Доказательство.По условию теоремы
т.е.
p
Pn 0,
q
n 1
n
p
p
p
n
an an 1 ... a1 a0 0. q
q
q
q
n
n 1
n 1
n
an p an 1 p q ... a1 pq a0 q 0.
Тогда
an p q(an 1 p
n
a0 q p(an p
n
n 1
n 1
... a1 pq
an 1 p
n 2
n 2
n 1
a0 q ), (1)
n 1
q ... a1q ). (2)
17.
Правая часть равенства (1) делится на q,значит и левая часть (1) делится на q.
p
Так как дробь
является несократимой, то p
q
не делится на q, а значит a n делится на q.
Аналогично, с помощью равенства (2)
показывается, что a0 делится на p.
18.
Пример. Решить уравнение2 x 3x 11x 6 0.
3
2
Решение. Применим теорему 4:
p : 1, 2, 3, 6;
q : 1, 2.
Возможные корни:
p
1
3
: 1, 2, 3, 6, , .
q
2
2
Проверим с помощью схемы Горнера, какие из
этих чисел являются корнями уравнения.
19.
2–3
– 11
1
2
–1
– 12
6 0
— не корень
–1
2
–5
–6
12 0
— не корень
2
2
1
–7
8 0
— не корень
–2
2
–7
3
6
0
Значит, x1 2 — корень уравнения.
Остальные корни можно найти из уравнения
2 x 7 x 3 0.
1
x2 , x3 3.
2
2
20.
п.2. Рациональные функции.Рациональной функцией называется
отношение двух многочленов.
n 1
Pn ( x) an x an 1 x ... a1 x a0
R( x)
.
m
n 1
Qm ( x) bm x bm 1 x ... b1 x b0
n
n m R(x)
n m R(x)
― правильная
рациональная дробь;
― неправильная
рациональная дробь.
21.
Пример.2
3
x 1
2
;
2
x 1 x 2 x 1 ( x 1)( x 2)( x 1)
4x x 6x 3
2 .
2
( x 1)( x 2)( x 1) x 1 x 2 x 1
3
2
22.
Всякую неправильную рациональную дробьпутем деления можно представить в виде
суммы многочлена и правильной
рациональной дроби.
Pn ( x)
Ps ( x)
n
m
T ( x)
,
s m
Qm ( x)
Qm ( x)
Пример.
2 x x 3x x 4 x 2
(см.
пример
2)
2
x 2x 3
75 x 76
3
2
2 x 3x 9 x 26 2
.
x 2x 3
5
4
3
2
23.
Простейшие рациональные дробиI.
A
x a
II.
III.
Mx N
,
2
x px q
IV.
p 4q 0
2
A
,
k 2
k
( x a) k N
Mx N
,
2
k
( x px q)
k 2 k N p 4q 0
A, M , N , a, p, q R
2
24.
Теорема 5.Всякую правильную рациональную дробь
Ps ( x)
, s m,
Qm ( x)
знаменатель которой разложен на множители
Qm ( x) ( x x1 ) ...( x xl )
kl
k1
( x p1 x q1 ) ...( x pt x qt ) ,
s1
2
D 0
st
2
D 0
можно представить (и притом единственным
образом) в виде суммы простейших дробей.
25.
Множителю вида ( x x1 ) соответствует суммаk простейших дробей
k
A3
Ak
A1
A2
...
.
2
3
k
x x1 ( x x1 ) ( x x1 )
( x x1 )
Множителю вида ( x px q) , p 4q 0,
соответствует сумма s простейших дробей
s
2
M s x Ns
M 1 x N1
M 2 x N2
2
... 2
.
2
2
s
x px q ( x px q)
( x px q)
26.
Пример. Разложить в сумму простейшихдробей
3
.
2
2
( x 1)( x 2) ( x x 1)
Решение.
3
2
2
( x 1)( x 2) ( x x 1)
A
B
C
Dx E
.
2
2
x 1 x 2 ( x 2)
x x 1
27.
Метод неопределенных коэффициентовПример. Разложить в сумму простейших
дробей
2
Решение.
2 x 3x 3
.
2
( x 1)( x 2 x 5)
2 x 3x 3
A
Bx C
2
2
( x 1)( x 2 x 5) x 1 x 2 x 5
2
A( x 2 x 5) ( Bx C )( x 1)
.
2
( x 1)( x 2 x 5)
2
28.
Приравняем конечный и исходный числитель,раскрыв скобки:
Ax 2 Ax 5 A Bx Bx Cx C 2 x 3x 3.
2
Выпишем слагаемые с x :
2
2
2
Ax Bx 2 x .
2
2
Получаем уравнение:
A B 2.
Выпишем слагаемые с x:
2 Ax Bx Cx 3x.
Получаем уравнение:
2 A B C 3.
2
29.
Выпишем слагаемые без x:5 A C 3.
Осталось решить систему:
A B 2,
2 A B C 3,
5 A C 3.
A 1, B 3, C 2.
Поэтому,
2 x 3x 3
1
3x 2
2
.
2
( x 1)( x 2 x 5) x 1 x 2 x 5
2
30.
Метод отдельных значений аргументаПример. Разложить в сумму простейших
дробей
Решение.
5x 4
.
x( x 1)( x 2)
5x 4
A
B
C
x( x 1)( x 2) x x 1 x 2
A( x 1)( x 2) Bx ( x 2) Cx( x 1)
.
x( x 1)( x 2)
31.
Приравняем конечный и исходный числитель:A( x 1)( x 2) Bx ( x 2) Cx( x 1) 5x 4.
Положим x 0 :
2 A 4; A 2.
Положим x 1 :
3B 9; B 3.
Положим x 2 :
6C 6; C 1.
Поэтому,
5x 4
2
3
1
.
x( x 1)( x 2) x x 1 x 2





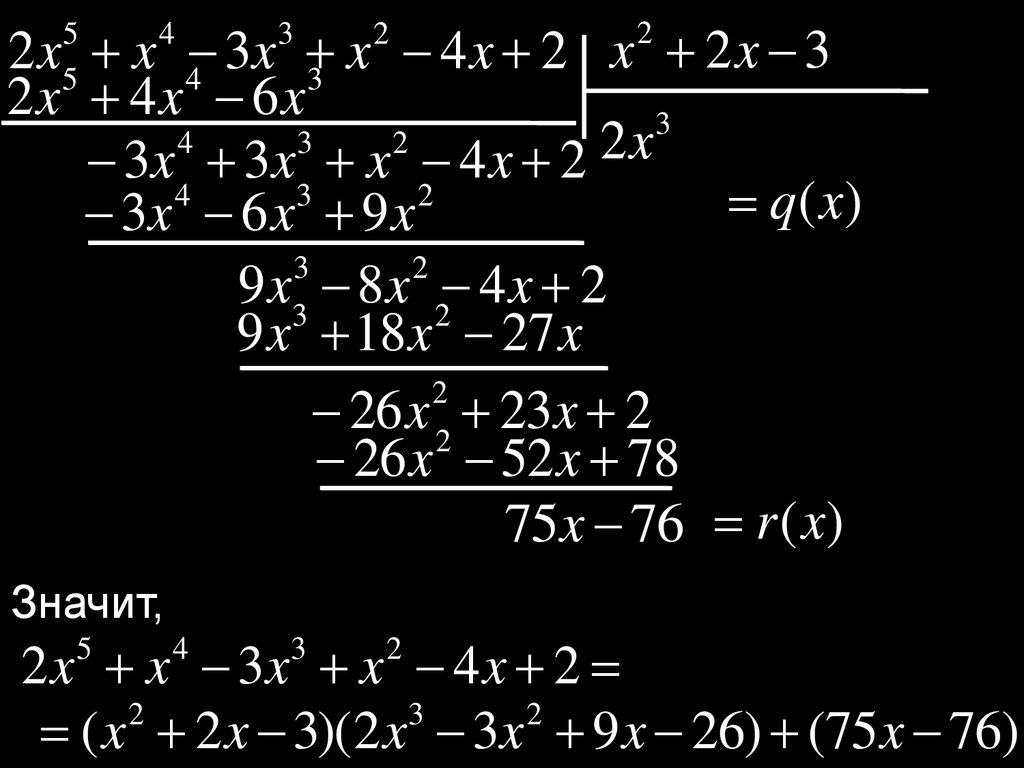

























 Математика
Математика








