Синус, косинус, тангенс двойного и половинного угла

1.

08.04.20
Классная работа
Синус, косинус,
тангенс двойного угла и
половинного
Глава VIII. §9,10

2.

Упростите полученные выражения
sin 2 sin( )
sin cos cos sin
cos 2 cos( )
cos cos sin sin
tg tg
tg 2 tg ( )
1 tg tg

3.

Запишите полученные формулы
sin 2 sin( )
sin cos cos sin 2 sin cos
cos 2 cos( )
cos cos sin sin cos sin
2
2
tg tg
2tg
tg 2 tg ( )
2
1 tg tg
1 tg

4.

Формулы двойного угла
sin 2 2 sin cos
cos 2 cos sin
2
2tg
tg 2
2
1 tg
2

5.

Стр.300, №1045 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin 48
2)tg92
5
3) cos
3

6.

Стр.300, №1045 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin 48 sin( 2 24 ) 2 sin 24 cos 24
2)tg92
5
3) cos
3

7.

Стр.300, №1045 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin 48 sin( 2 24 ) 2 sin 24 cos 24
2tg 46
2)tg92 tg (2 46 )
1 tg 2 46
5
3) cos
3

8.

Стр.300, №1045 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin 48 sin( 2 24 ) 2 sin 24 cos 24
2tg 46
2)tg92 tg (2 46 )
2
1 tg 46
5
5
3) cos
cos( 2
)
3
6

9.

Стр.300, №1045 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin 48 sin( 2 24 ) 2 sin 24 cos 24
2tg 46
2)tg92 tg (2 46 )
2
1 tg 46
5
5
2 5
2 5
sin
3) cos
cos( 2
) cos
6
6
3
6

10.

Стр.300, №1046 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin(
2
)
Пошаговая
проверка

11.

Стр.300, №1046 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin(
2
) sin( 2 (
4
2
))

12.

Стр.300, №1046 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
1) sin(
) sin( 2 (
4 2
2 sin( ) cos( )
4 2
4 2
2
))

13.

Стр.300, №1046 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
3) cos(
2
)

14.

Стр.300, №1046 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
3) cos(
2
) cos 2(
4
2
)
cos ( ) sin ( )
4 2
4 2
2
2

15.

Стр.300, №1046 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
5) sin

16.

Стр.288, №122 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
5) sin sin 2
2
2 sin
2
cos
2

17.

Стр.300, №1046 (1,3,5)
Выразить синус, косинус и тангенс,
используя формулы двойного угла
5) sin sin 2
2
2 sin
2
cos
2

18.

Стр.300, №1047 (1,3)
Вычислить, не используя
калькулятора
1)2 sin 15 cos15
2tg15
3)
2
1 tg 15

19.

Стр.300, №1047 (1,3)
Вычислить, не используя
калькулятора
1
1)2 sin 15 cos15 sin 30
2
2tg15
3
3)
tg30
2
1 tg 15
3

20.

Стр.301, №1048 (2)
Вычислить, не используя
калькулятора
2
2) cos sin
8
8
2

21.

Стр.301, №1048 (2)
Вычислить, не используя
калькулятора
2
2
2) cos sin
cos( 2 ) cos
8
8
8
4
2
2
2
2
4)
(cos sin )
2
8
8

22.

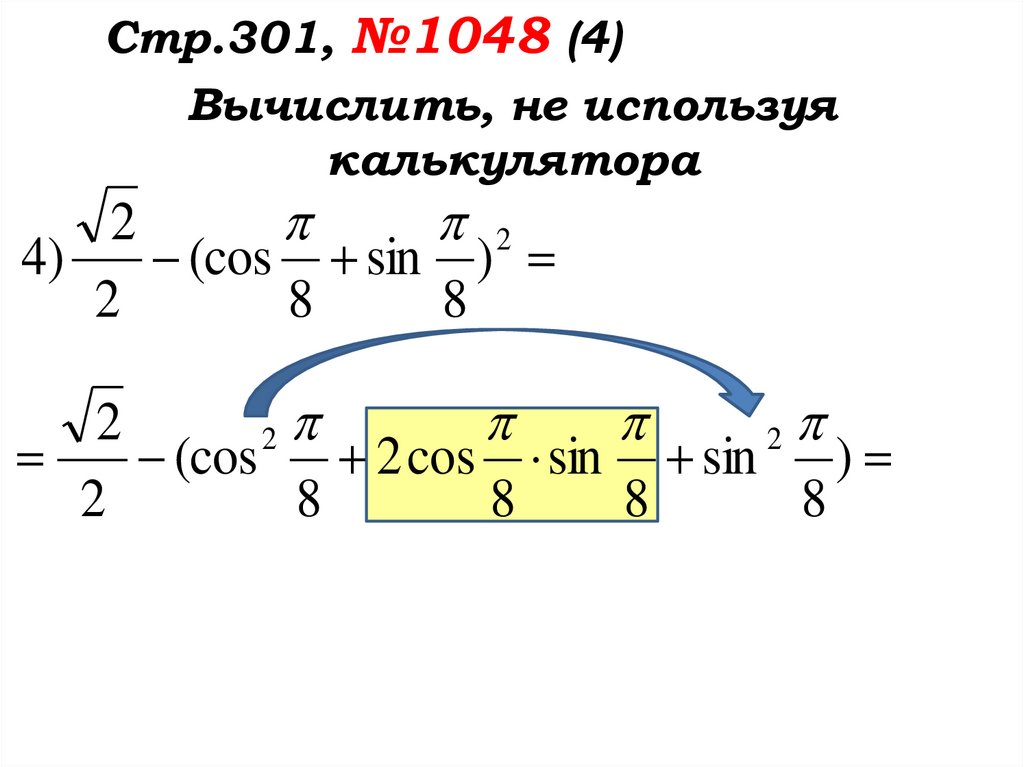
Стр.301, №1048 (4)
Вычислить, не используя
калькулятора
2
2
4)
(cos sin )
2
8
8
2
2
2
(cos 2 cos sin sin )
2
8
8
8
8

23.

Стр.301, №1048 (4)
Вычислить, не используя
калькулятора
2
2
4)
(cos sin )
2
8
8
2
2
2
(cos 2 cos sin sin )
2
8
8
8
8

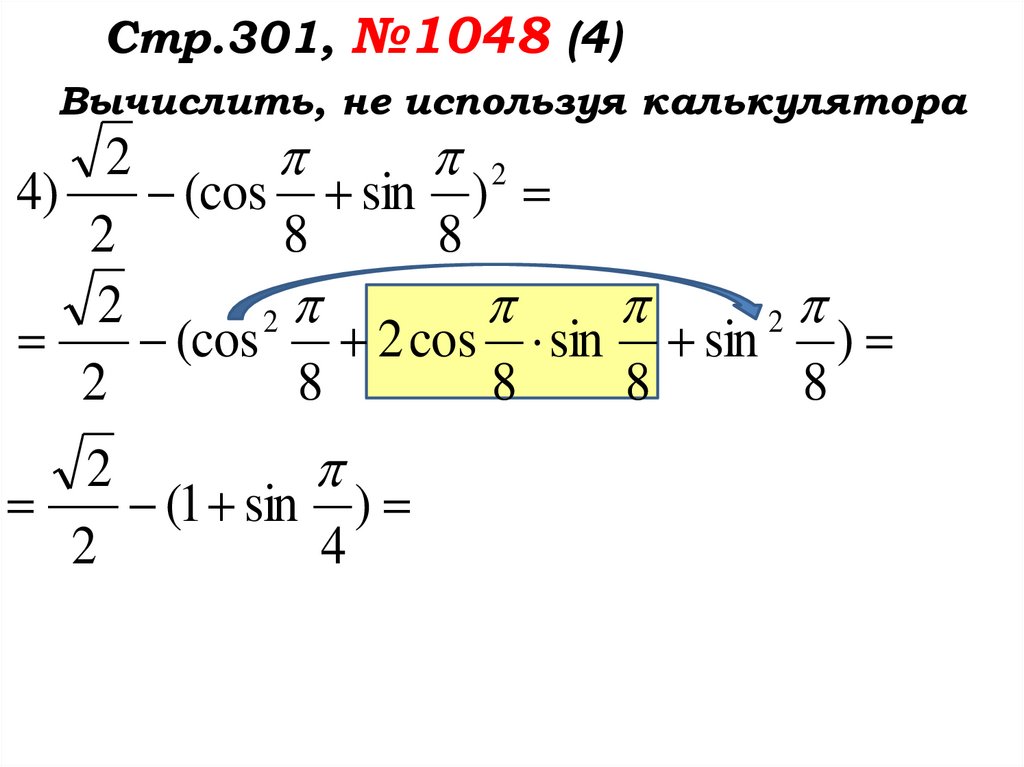
24.

Стр.301, №1048 (4)
Вычислить, не используя калькулятора
2
2
4)
(cos sin )
2
8
8
2
2
2
(cos 2 cos sin sin )
2
8
8
8
8
2
(1 sin )
2
4

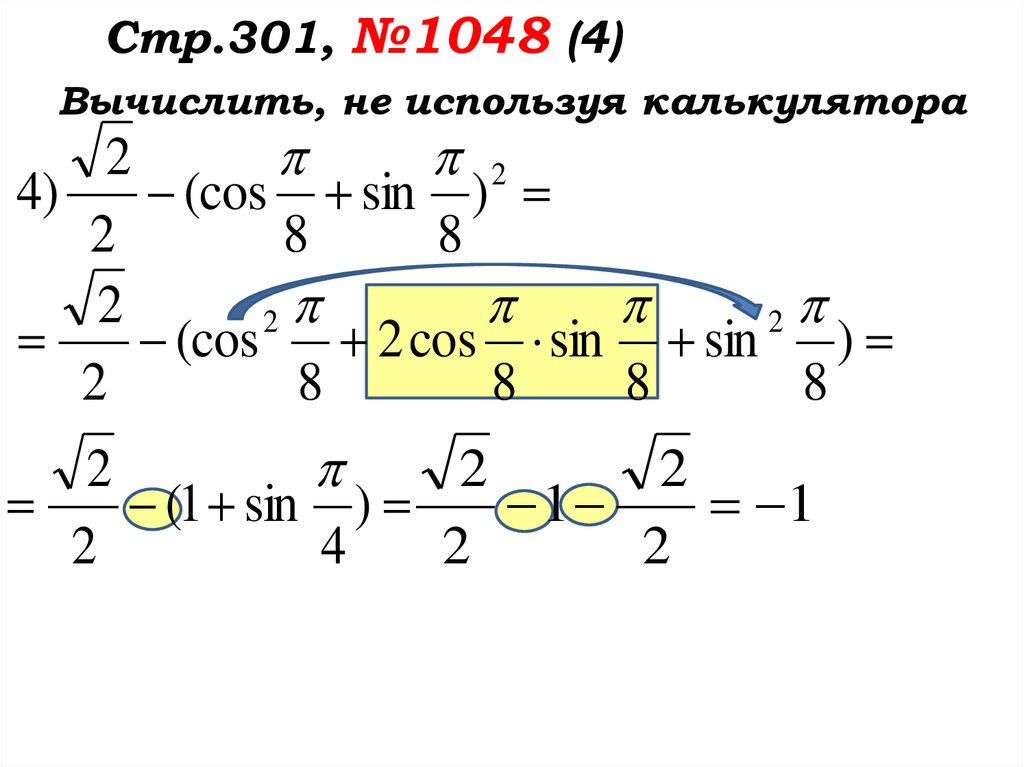
25.

Стр.301, №1048 (4)
Вычислить, не используя калькулятора
2
2
4)
(cos sin )
2
8
8
2
2
2
(cos 2 cos sin sin )
2
8
8
8
8
2
2
2
(1 sin )
1
1
2
4
2
2

26.

Стр.301, №1050(1)
3
Вычислить sin 2 , если sin ;
5
2
Решение:
cos ...
sin 2 ...
Проверка

27.

Стр.301, №1050(1)
3
Вычислить sin 2 , если sin ;
5
2
Решение:
3 2
4
cos 1 ( )
5
5
3
4
24
sin 2 2 ( )
5
5
25

28.

Замените угол разностью,
заполнив пропуски:
cos 40 cos(90 ...)
sin 50 sin( 90 ...)
sin 20 sin( 90 ...)
cos15 cos(90 ...)

29.

Замените угол разностью,
заполнив пропуски:
cos 40 cos(90 40 )
sin 50 sin( 90 40 )
sin 20 sin( 90 70 )
cos15 cos(90 75 )

30.

Запишите в тетрадь формулы
Задачи №3, стр.283
cos( )
2
sin( )
2

31.

Заполните пропуски:
cos( ) sin
2
sin( ) cos
2
cos(90 )
sin( 90 )

32.

Формулы замены
синуса на косинус или
косинуса на синус
cos( ) sin
2
cos(90 ) sin
sin( ) cos
2
sin( 90 ) cos

33.

Стр.301, №1053 (1)
2 cos 40 cos 50
Обсудите в паре и дайте
рекомендации для решения

34.

Стр.301, №1053(1)
2 cos 40 cos 50 2 sin 50 cos 50 sin 100
40 50 90
углы, дополняющие друг друга до 90º

35.

Запишите угол, дополняющий
данный угол до 90º или
10 и ...
86 и ...
и
и
и
3
2

36.

Углы, дополняющие друг друга до 90ºили
10
и 90 10 80
86 и
4
и
2
и
2
и
3
2 3
2

37.

Стр.301, №1054(1)
Упростить выражение
sin 2
2
(sin cos ) 1

38.

Стр.301, №1054(1)
Упростить выражение
sin 2
2
(sin cos ) 1
sin 2
2
2
sin 2 sin cos cos 1

39.

Стр.301, №1054(1)
Упростить выражение
sin 2
2
(sin cos ) 1
sin 2
2
2
sin 2 sin cos cos 1
sin 2
2 sin cos

40.

Стр.301, №1054(1)
Упростить выражение
sin 2
2
(sin cos ) 1
sin 2
2
2
sin 2 sin cos cos 1
sin 2
1
2 sin cos

41.

Стр.301, №1054(2)
Упростить выражение
1 cos 2
1 cos 2

42.

Стр.301, №1054(2)
Упростить выражение
1 cos 2 1 (cos sin )
2
2
1 cos 2 1 (cos sin )
2
2

43.

Стр.301, №1054(2)
Упростить выражение
1 cos 2 1 (cos sin )
2
2
1 cos 2 1 (cos sin )
2
1 cos sin
2
2
1 cos sin
2
2
2

44.

Стр.301, №1054(2)
Упростить выражение
1 cos 2 1 (cos sin )
2
2
1 cos 2 1 (cos sin )
2
2
1 cos sin cos 1 sin
2
2
2
2
1 cos sin 1 cos sin
2
2
2
2

45.

Стр.301, №1054(2)
Упростить выражение
1 cos 2 1 (cos sin )
2
2
1 cos 2 1 (cos sin )
2
2
1 cos sin cos 1 sin
2
2
2
2
1 cos sin 1 cos sin
2
2
cos cos
2
2
sin sin
2
2
2
2

46.

Стр.301, №1054(2)
Упростить выражение
1 cos 2 1 (cos sin )
2
2
1 cos 2 1 (cos sin )
2
2
1 cos sin cos 1 sin
2
2
2
2
1 cos sin 1 cos sin
2
2
2
cos cos 2 cos
2
2
2
sin sin 2 sin
2
2
2
2

47.

Стр.301, №1054(2)
Упростить выражение
1 cos 2 1 (cos sin )
2
2
1 cos 2 1 (cos sin )
2
2
1 cos sin cos 1 sin
2
2
2
2
1 cos sin 1 cos sin
2
2
2
cos cos 2 cos
2
сtg
2
2
2
sin sin 2 sin
2
2
2
2

48.

Стр.301, №1056(1)
1
Вычислить sin 2 , если sin cos
2

49.

Стр.301, №1056(1)
1
Вычислить sin 2 , если sin cos
2
(sin cos )
2

50.

Стр.301, №1056(1)
1
Вычислить sin 2 , если sin cos
2
Ваши предложения по решению
(sin cos ) sin 2 sin cos cos
2
2
2

51.

Стр.301, №1056(1)
1
Вычислить sin 2 , если sin cos
2
Ваши предложения по решению
(sin cos ) sin 2 sin cos cos
2
2
1 sin 2 ...
2

52.

Стр.301, №1056(1)
1
Вычислить sin 2 , если sin cos
2
Ваши предложения по решению
(sin cos ) sin 2 sin cos cos
1
1 sin 2
4
2
sin 2 ...
2
2

53.

Стр.301, №1056(1)
1
Вычислить sin 2 , если sin cos
2
Ваши предложения по решению
(sin cos ) sin 2 sin cos cos
1
1 sin 2
4
1
3
sin 2 1
4
4
2
2
2

54.

Стр.302, №1059(3)
Решить уравнение
4 cos x sin 2x
Ваши предложения по решению

55.

Стр.302, №1059(3)
Решить уравнение: 4 cos x sin 2x
Решение:
4 cos x sin 2x 0

56.

Стр.302, №1059(3)
Решить уравнение: 4 cos x sin 2x
Решение:
4 cos x sin 2x 0
4 cos x 2 sin x cos x 0

57.

Стр.302, №1059(3)
Решить уравнение: 4 cos x sin 2x
Решение:
4 cos x sin 2x 0
4 cos x 2 sin x cos x 0
cos x(4 2 sin x) 0

58.

Стр.302, №1059(3)
Решить уравнение: 4 cos x sin 2x
Решение:
4 cos x sin 2x 0
4 cos x 2 sin x cos x 0
cos x(4 2 sin x) 0
cos x 0; 4 2 sin x 0

59.

Стр.302, №1059(3)
Решить уравнение: 4 cos x sin 2x
Решение:
4 cos x sin 2x 0
4 cos x 2 sin x cos x 0
cos x(4 2 sin x) 0
cos x 0;
4 2 sin x 0
x k , k R
2

60.

Стр.302, №1059(3)
Решить уравнение: 4 cos x sin 2x
Решение:
4 cos x sin 2x 0
4 cos x 2 sin x cos x 0
cos x(4 2 sin x) 0
cos x 0;
4 2 sin x 0
sin x 2
x k , k R
2

61.

Стр.302, №1059(3)
Решить уравнение: 4 cos x sin 2x
Решение:
4 cos x sin 2x 0
4 cos x 2 sin x cos x 0
cos x(4 2 sin x) 0
4 2 sin x 0
cos x 0;
sin
x
2
x k , k R
Корней нет
2
Ответ : x
2
k , k R

62.

Средний балл за урок:
«5»- все было понятно и задания
выполнялись без особого труда;
«4» – были трудные моменты, осталось
еще раз разобрать задания, чтобы не было
проблем в будущем;
«3»- остались непонятными некоторые
задания из-за пробелов в знаниях. Следует
поработать индивидуально.
Оцените усвоение материала
в классе

63.

Домашнее задание
1. Рассмотреть презентацию
2. Решение задач переписать в
тетрадь
3. Выполнить проверочную работу на
якласс.