Математическая статистика

1.

Математическая статистики — раздел математики,
изучающий методы обработки и анализа данных с
целью принятия обоснованных решений.

2.

Генеральная совокупность и выборка
Генеральная совокупность – вся
интересующая исследователя совокупность
изучаемых объектов.
Выборка – некоторая, обычно небольшая,
часть генеральной совокупности, исследуемая с
целью получения выводов о свойствах всей
генеральной совокупности.

3.

Генеральная совокупность и выборка
Репрезентативная
выборка хорошо представляет
генеральную совокупность. Это означает, что
каждое свойство (или комбинация свойств)
наблюдается в выборке с той же частотой, что и в
генеральной совокупности.
Параметры
— это количественные показатели,
характеризующий всю генеральную совокупность.
Оценки
параметров - количественные
показатели, вычисленные по выборке .

4.

Генеральная совокупность и выборка

5.

Пусть Х – дискретный признак.
Cделана выборка
x1 , x2 ,
xn
где
n - объем выборки.
Составляется ряд распределения

6.

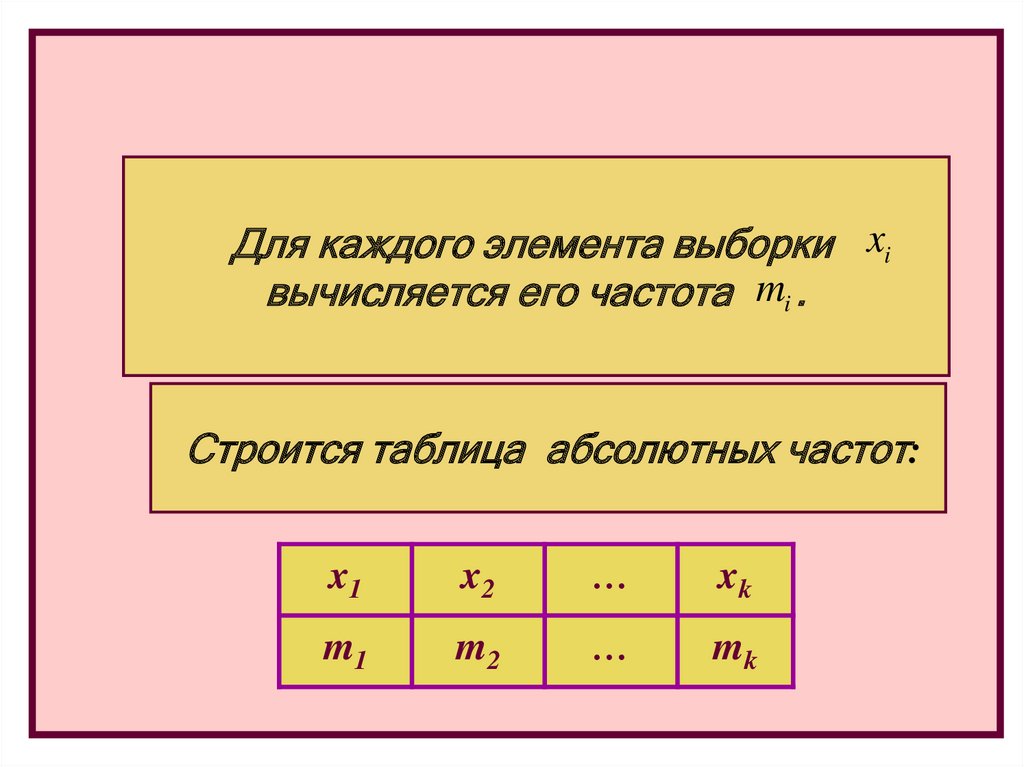
Для каждого элемента выборки xi
вычисляется его частота mi .
Строится таблица абсолютных частот:
x1
x2
…
xk
m1
m2
…
mk

7.

рассчитываем относительные частоты :
Причем
m
i
i
mi
pi
n
n
p
i
i
1

8.

Строится таблица относительных частот:
x1
x2
…
xk
p1
p2
…
pk

9.

Пример: 30 посетителей гипермаркета
попросили ответить на вопрос: сколько раз в
неделю в среднем они посещают
гипермаркет. Получили дискретную
выборку:
1,3,4,4,5,6,3,5,7,1,4,0,3,7,5,6,2,1,4,2,6,4,5,7,1,4,2,
3,5,3

10.

Пример: 30 посетителей гипермаркета
попросили ответить на вопрос: сколько раз в
неделю в среднем они посещают
гипермаркет. Получили дискретную
выборку:
1,3,4,4,5,6,3,5,7,1,4,0,3,7,5,6,2,1,4,2,6,4,5,7,1,4,2,
3,5,3
Таблица абсолютных частот
X
0
1
2
3
4
5
6
7
m
1
4
3
5
6
5
3
3

11.

Пример: 30 посетителей гипермаркета
попросили ответить на вопрос: сколько раз в
неделю в среднем они посещают
гипермаркет. Получили дискретную
выборку:
1,3,4,4,5,6,3,5,7,1,4,0,3,7,5,6,2,1,4,2,6,4,5,7,1,4,2,
3,5,3 X 0 1 2 3 4 5 6 7
m
1
4
p
1
4
30 30
3
3
30
5
6
5 6
30 30
5
3
5 3
30 30
3
3
30

12.

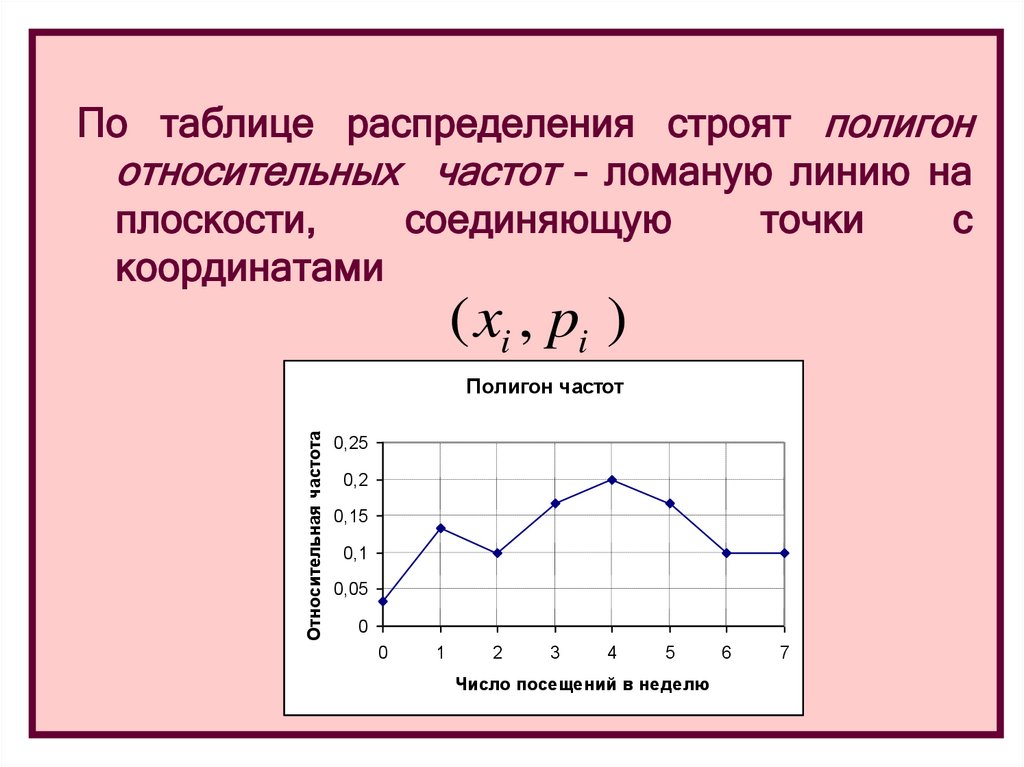
По таблице распределения строят полигон
относительных частот – ломаную линию на
плоскости,
соединяющую
точки
с
координатами
( xi , pi )
Относительная частота
Полигон частот
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
Число посещений в неделю
6
7

13.

Полигон частот, построенный по выборке
является оценкой распределения случайной
величины X – числа посещений гипермаркета
рядовым покупателем.
Относительная частота
Полигон частот
0,25
0,2
0,15
0,1
0,05
0
0
1
2
3
4
5
Число посещений в неделю
6
7

14.

Задание 1
100 человек, посмотревших новый фильм,
попросили оценить его. Результаты
оценки представлены в файле film.

15.

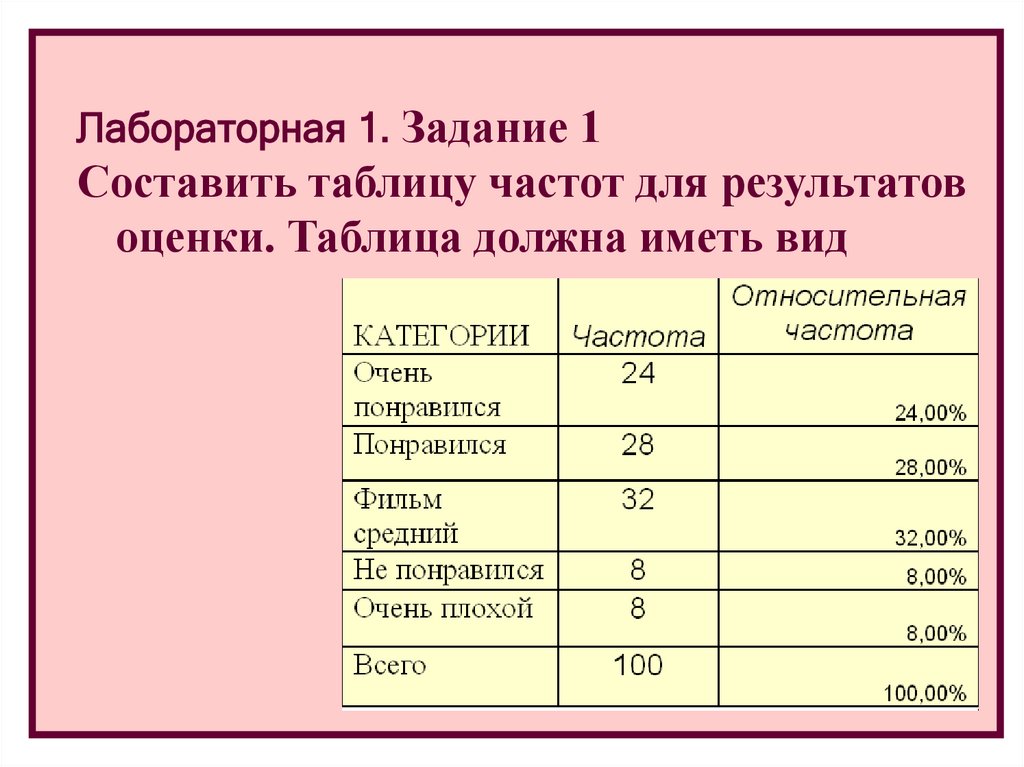
Лабораторная 1. Задание 1
Составить таблицу частот для результатов
оценки. Таблица должна иметь вид

16.

Лабораторная 1. Задание 1
Для вычисления абсолютных частот
можно использовать функцию
СЧЕТЕСЛИ

17.

Лабораторная 1. Задание 1
Для вычисления абсолютных частот
можно использовать функцию
СЧЕТЕСЛИ

18.

Лабораторная 1. Задание 1
Для вычисления абсолютных частот
можно использовать функцию
СЧЕТЕСЛИ
Относительную
частоту вычисляем
разделив абсолютную
частоту на объем
выборки. Устанавливаем
процентный формат
ячеек

19.

Представить частоты в виде гистограммы
и круговой диаграммы.
45
40
35
30
25
20
15
10
5
0
Очень
понравился
Понравился
Средний
фильм
Не
понравился
Оченть
плохой
45,00%
40,00%
35,00%
30,00%
25,00%
20,00%
15,00%
10,00%
5,00%
0,00%
Очень
понравился
Понравился
Средний
фильм
Не
понравился
Оченть
плохой

20.

Представить частоты в виде гистограммы
и круговой диаграммы.
9
0
11
Очень понравился
Понравился
Средний фильм
30
42
Не понравился
Оченть плохой
9,00% 0,00% 11,00%
Очень понравился
Понравился
Средний фильм
30,00%
42,00%
Не понравился
Оченть плохой

21.

Пусть Х – непрерывный признак.
Cделана выборка x1 , x2 , xn
составляется интервальный ряд
распределения

22.

a min xi
b max xi
В Excel есть функции МИН и МАКС

23.

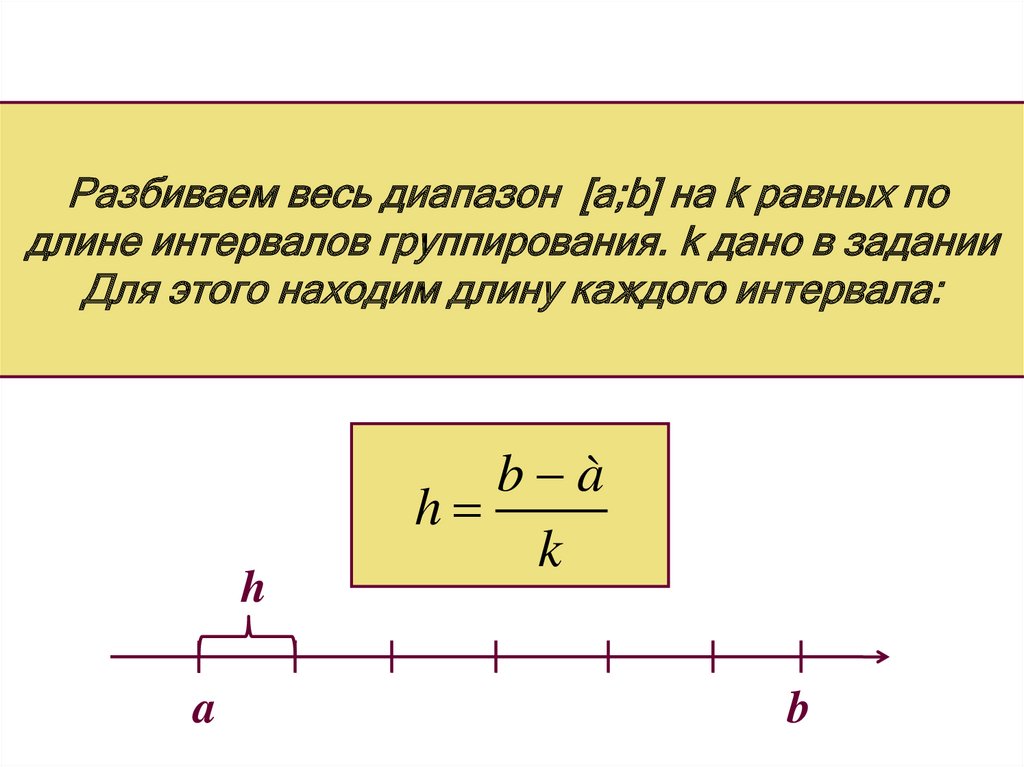
Разбиваем весь диапазон [a;b] на k равных по
длине интервалов группирования. k дано в задании
Для этого находим длину каждого интервала:
h
a
b à
h
k
b

24.

Устанавливается шкала интервалов
a1 a, a2 a1 h, a3 a2 h, ... ak h b
h
a1
a2
ak
b

25.

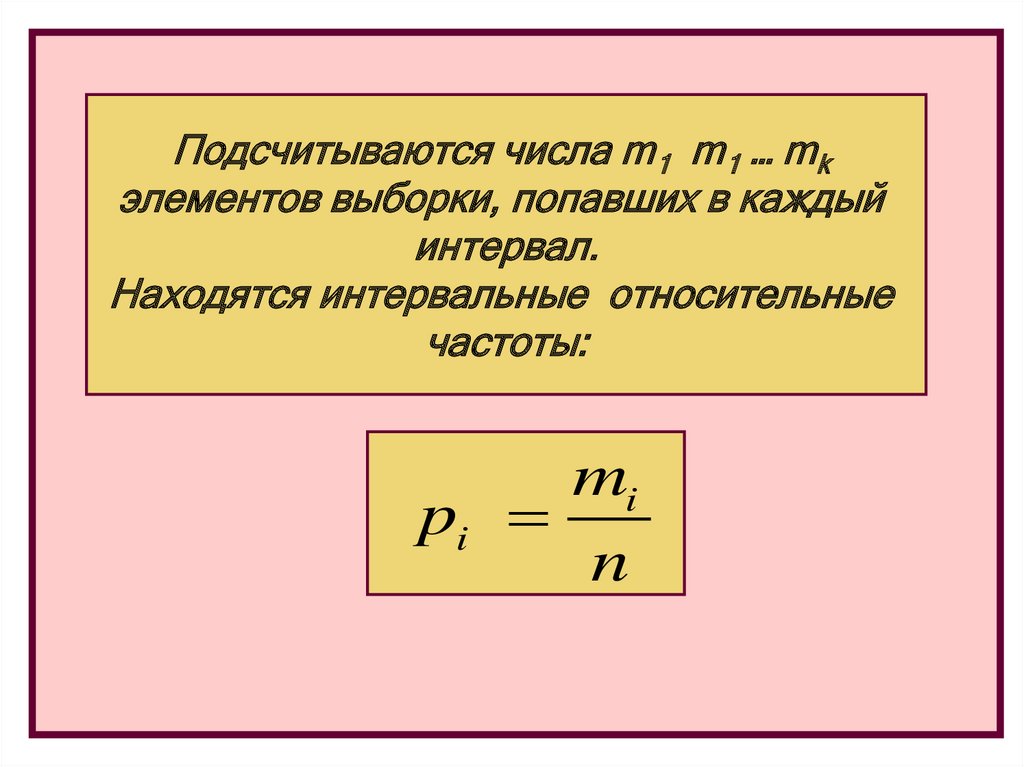
Подсчитываются числа m1 m1 … mk
элементов выборки, попавших в каждый
интервал.
Находятся интервальные относительные
частоты:
mi
pi
n

26.

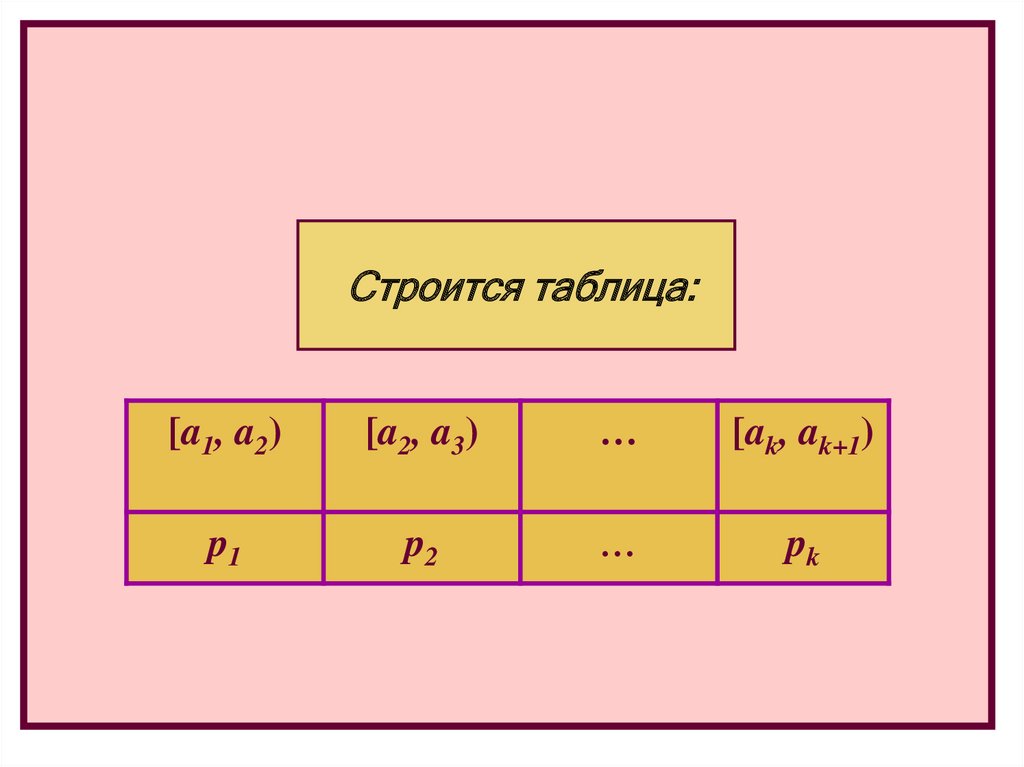
Строится таблица:
[a1, a2)
[a2, a3)
…
[ak, ak+1)
p1
p2
…
pk

27.

Эта таблица и называется ИНТЕРВАЛЬНЫМ
РЯДОМ РАСПРЕДЕЛЕНИЯ.
По ней можно построить гистограмму частот.

28.

Задание 2
В файле flat представлены данные о
ценах на однокомнатные квартиры
(тыс. USD), выставлявшихся на
продажу в Москве.

29.

Задание 2
В файле flat представлены данные о
ценах на однокомнатные квартиры
(тыс. USD), выставлявшихся на
продажу в Москве.
1. Найдите минимальную и максимальную
цену
Функции МИН и МАКС

30.

Задание 2
В файле flat представлены данные о
ценах на однокомнатные квартиры
(тыс. USD), выставлявшихся на
продажу в Москве.
2. Найдите ширину интервала при
разбиении всего диапазона цен на 10
интервалов.

31.

3. Вычислите левые и правые границы
всех 10 интервалов.

32.

3. Вычислите левые и правые границы
всех 10 интервалов.

33.

3. Вычислите левые и правые границы
всех 10 интервалов.

34.

Найдите
абсолютные
частоты
попадания в интервалы с помощью
функции ЧАСТОТА.
Выделите ячейки, в которых будут
храниться частоты и одну ячейку ниже
4.

35.

36.

Массив с правыми границами

37.

Заверщаем формулу нажатием
Ctrl+Shift+Enter (одновременно)

38.

Цену от 27 тыс. USD до 31,4 тыс. USD
имеют 9 квартир в выборке.

39.

5. Найдите относительные частоты.
Дайте экономическую интерпретацию
полученным значениям
Цену от 27 тыс. USD до 31,4 тыс. USD
Имеют 13% квартир в выборке.

40.

6. Найдите накопленные относительные
частоты. Дайте экономическую
интерпретацию полученным значениям
(достаточно интерпретировать одну
строку, только не первую)

41.

64% квартир в выборке имеет цену от 27
тыс. USD до 40,2 тыс. USD

42.

7. Постройте гистограммы абсолютных и
относительных частот. Для построения
гистограммы воспользуйтесь мастером
диаграмм. На корешке вкладки
Стандартные выберите в списке диаграмм
пункт Гистограмма - обычная.
В качестве Диапазона данных задайте
массив с частотами. В качестве подписей
по оси X укажите массив с правыми
границами.

43.

Гистограммы абсолютных и относительных
частот
Частота
25
20
15
Частота
10
5
0
32,70 37,40 42,10 46,80 51,50 56,20 60,90 65,60 70,30 75,00
35%
30%
25%
20%
15%
10%
5%
32
,7
0
37
,4
0
42
,1
0
46
,8
0
51
,5
0
56
,2
0
60
,9
0
65
,6
0
70
,3
0
75
,0
0
0%
Относительная частота

44.

8. Постройте полигон относительных
частот. Чтобы построить полигон,
воспользуйтесь мастером диаграмм.
На корешке вкладки Стандартные
выберите в списке диаграмм пункт
График с маркерами. В качестве
Диапазона данных задайте массив с
относительными частотами.
В качестве подписей по оси X укажите
массив с правыми границами.

45.

Относительная частота
35%
30%
25%
20%
15%
Относительная
частота
10%
5%
0%
0
0
0
0
0
0
0
0
0
0
, 7 7, 4 2, 1 6, 8 1, 5 6, 2 0, 9 5, 6 0, 3 5, 0
2
3
3
4
4
5
5
6
6
7
7
Полигон относительных частот

46.

9. Постройте кумуляту
(график накопленных относительных
частот). По оси Х должны быть правые
границы, по оси Y накопленные
относительные частоты.
Накопленная относительная частота
120%
100%
80%
60%
40%
20%
32
,7
0
37
,4
0
42
,1
0
46
,8
0
51
,5
0
56
,2
0
60
,9
0
65
,6
0
70
,3
0
75
,0
0
0%
Накопленная
относительная
частота