Векторная алгебра

1. Векторная алгебра

Часть 2

2. Скалярное произведение

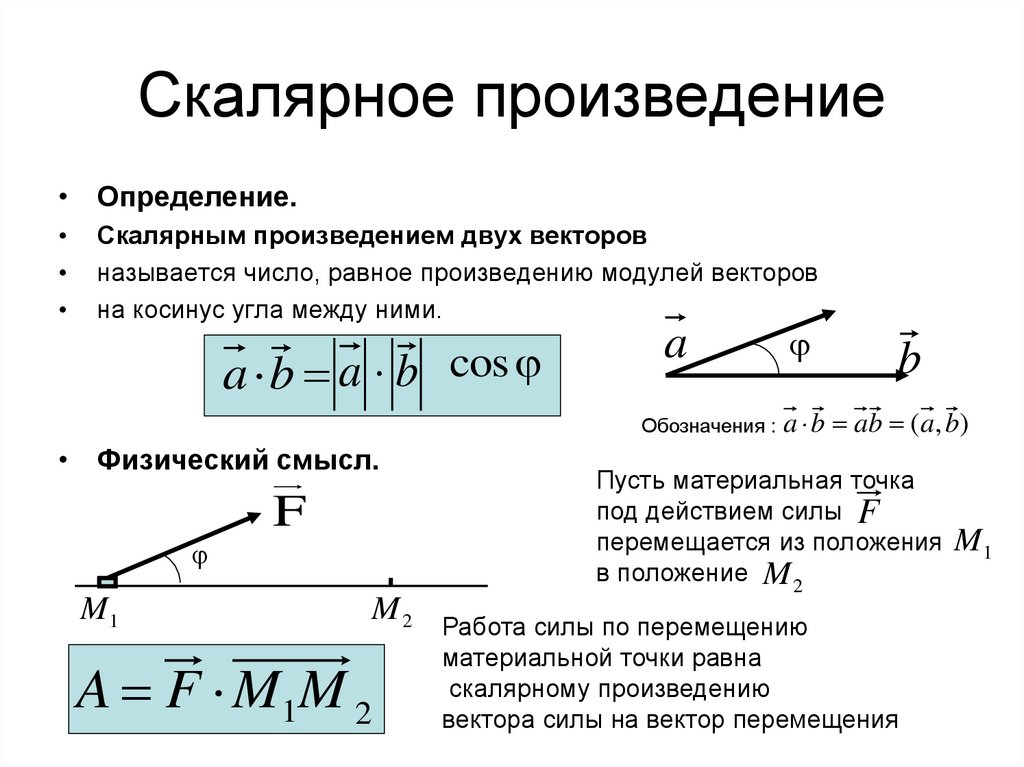
• Определение.
Скалярным произведением двух векторов
называется число, равное произведению модулей векторов
на косинус угла между ними.
a b a b cos
a
Обозначения :
• Физический смысл.
F
M1
M2
A F M 1M 2
b
a b ab ( a, b)
Пусть материальная точка
под действием силы F
перемещается из положения
в положение M 2
Работа силы по перемещению
материальной точки равна
скалярному произведению
вектора силы на вектор перемещения
M1

3.

• Свойства скалярного произведения.
• 1.
- переместительный закон
a b b a
• 2. ( a ) b (a b)
- сочетательный закон
• 3. a b | a | Пр b | b | Пр a
a
b

4.

Доказательство свойства № 3.
a b | a | | b | cos | a | Прa b,
так как по третьему свойству проекций Прa b | b | cos .
Аналогично можно записать
a b | b | | a | cos | b | Прb a .
Следствие
Прb a
a b
b
Прa b
a b
a

5. 4. - распределительный закон

4. (a b) c a c b c - распределительный закон
• Доказательство свойства № 4.
(a b) c | c | Пр.c (a b) | c | (Пр.c a Пр.c b)
| c | Пр.c a | c | Пр.c b a c b c.

6. Свойства скалярного произведения (продолжение)

cos
• 5.
• 6.
2
2
a a ,
a b
a b
2
так как a a a | a | | a | cos 0 | a |2 .
(| a | a ).
Скалярный квадрат вектора равен квадрату его модуля.
• 7. Условие перпендикулярности векторов.
2
Для того, чтобы два ненулевых вектора были
перпендикулярны необходимо и достаточно,
чтобы скалярное произведение этих векторов
равнялось нулю:
a b a b 0
Определение
перпендикулярных
векторов:
90°

7. Доказательство.

Необходимость: если a b 0, то | a ||b | cos 0, т.к. a 0, b 0, то cos 0 ,
значит 90o.
Достаточность: если
90
o
, то
cos 0,
и
a b 0.

8. Пример.

Найти модуль вектора
c 2a 3b , если a 4, b 5 и угол между
o
a
и
b
60
.
векторами
Решение.
Находим скалярный квадрат вектора c :
2
2
2
c (2a 3b)2 4a 12a b 9b
4 | a |2 12 | a ||b| cos 60o 9 |b|2
4 16 12 4 5
1
9 25 409,
2
| c |
409 .

9.

Скалярное произведение ортов
Так как орты
равно нулю:
i и j
i , j, k
перпендикулярны, то их скалярное произведение
i j 0
i k 0
аналогично,
j k 0
Скалярные квадраты ортов i , j, k :
2
2
2
i 1, j 1, k 1

10. Скалярное произведение векторов, заданных в координатной форме.

• Пусть a x1 , y1 , z1 и b x2 , y2 , z2
• Тогда a b x1 x2 y1 y2 z1 z2
Скалярное произведение векторов равно
сумме произведений соответствующих координат.

11. Доказательство.

Дано: a {X1; Y1; Z1} и b {X 2 ; Y2 ; Z2} или a X1 i Y1 j Z1k и b X 2 i Y2 j Z2k .
Вычислим их скалярное произведение a b. Воспользуемся
распределительным и сочетательным свойствами скалярного
произведения (свойством 4 и свойством 2) и получим:
a b X1X 2 i i Y1X 2 j i Z1X 2k i
X1Y2 i j Y1Y2 j j Z1Y2k j
X1Z2 i k Y1Z2 j k Z1Z2k k.
Встречающиеся здесь скалярные квадраты базисных векторов
равны единице, т.к. i i | i |2 1, j j | j |2 1, k k | k |2 1.

12. Все остальные скалярные произведения базисных векторов равны нулю, т.к. являются скалярными произведениями перпендикулярных

векторов
(свойство 7).
Окончательно получается
a b X1X 2 Y1Y2 Z1Z2
Можно формулировать следующее правило.
Если векторы заданы своими прямоугольными координатами, то
скалярное произведение векторов равно сумме произведений
одноименных координат этих векторов:
a b X1X 2 Y1Y2 Z1Z2

13. В частности,

a 2 a a X12 Y12 Z12 , а т.к.|a| a 2 , то |a| X12 Y12 Z12
Правило вычисления длины вектора.
Длина вектора равна квадратному корню из суммы квадратов координат
этого вектора:
|a| X12 Y12 Z12

14. Условие перпендикулярности векторов в координатной форме :

Условие перпендикулярности векторов
в координатной форме :
a b x1 x2 y1 y2 z1 z 2 0

15. Пример.

a {-1;2;5}, b {2;3;4}. Тогда a b -1 2 2 3 5 4 24.
Задачи

16. Правые и левые тройки векторов.

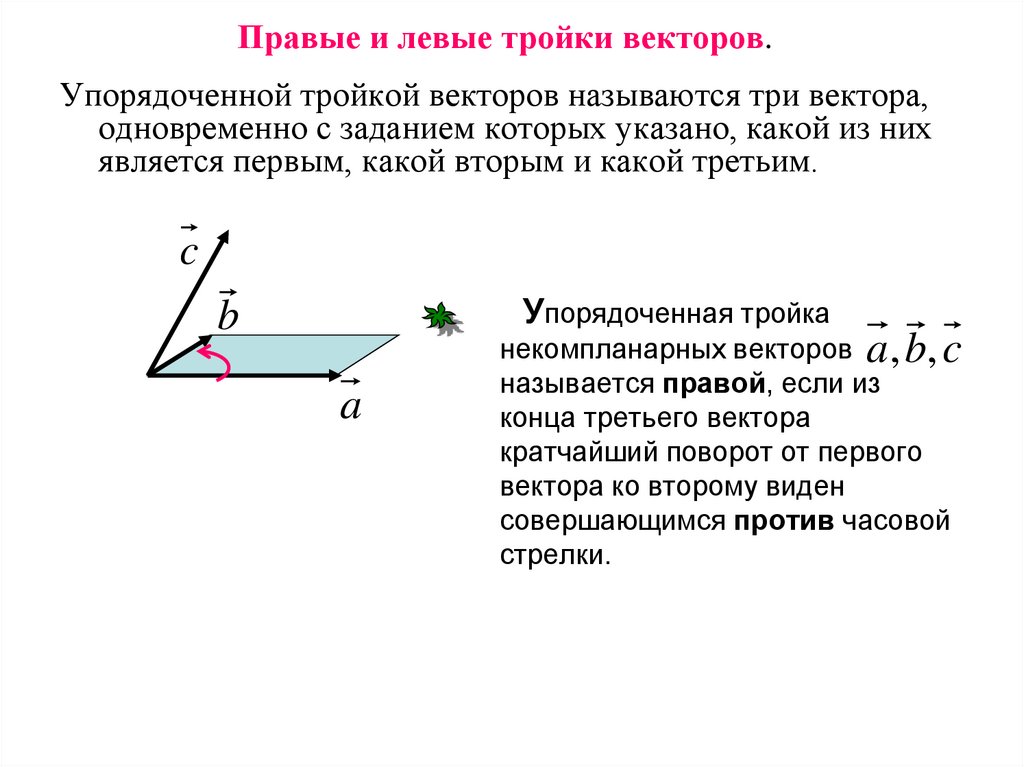
Упорядоченной тройкой векторов называются три вектора,
одновременно с заданием которых указано, какой из них
является первым, какой вторым и какой третьим.
c
Упорядоченная тройка
b
a
некомпланарных векторов a , b, c
называется правой, если из
конца третьего вектора
кратчайший поворот от первого
вектора ко второму виден
совершающимся против часовой
стрелки.

17. Векторное произведение

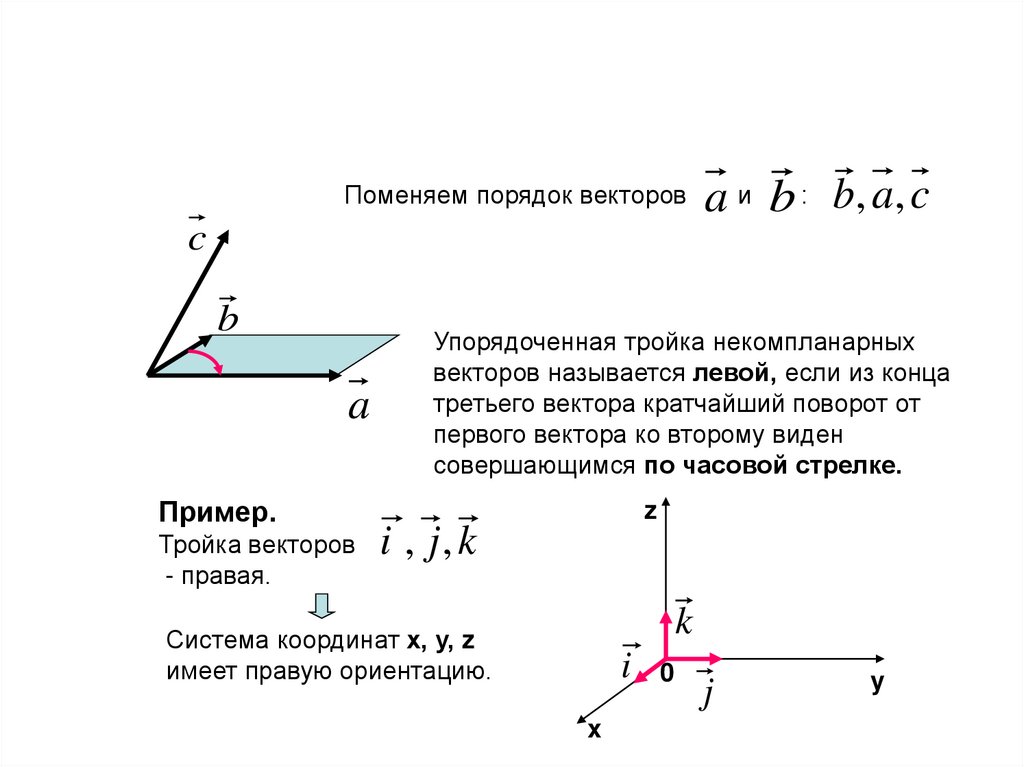
Поменяем порядок векторов
a и b : b, a , c
c
b
a
Пример.
Тройка векторов
- правая.
Упорядоченная тройка некомпланарных
векторов называется левой, если из конца
третьего вектора кратчайший поворот от
первого вектора ко второму виден
совершающимся по часовой стрелке.
z
i , j, k
k
Система координат х, у, z
имеет правую ориентацию.
i
x
0
j
y

18. Векторное произведение

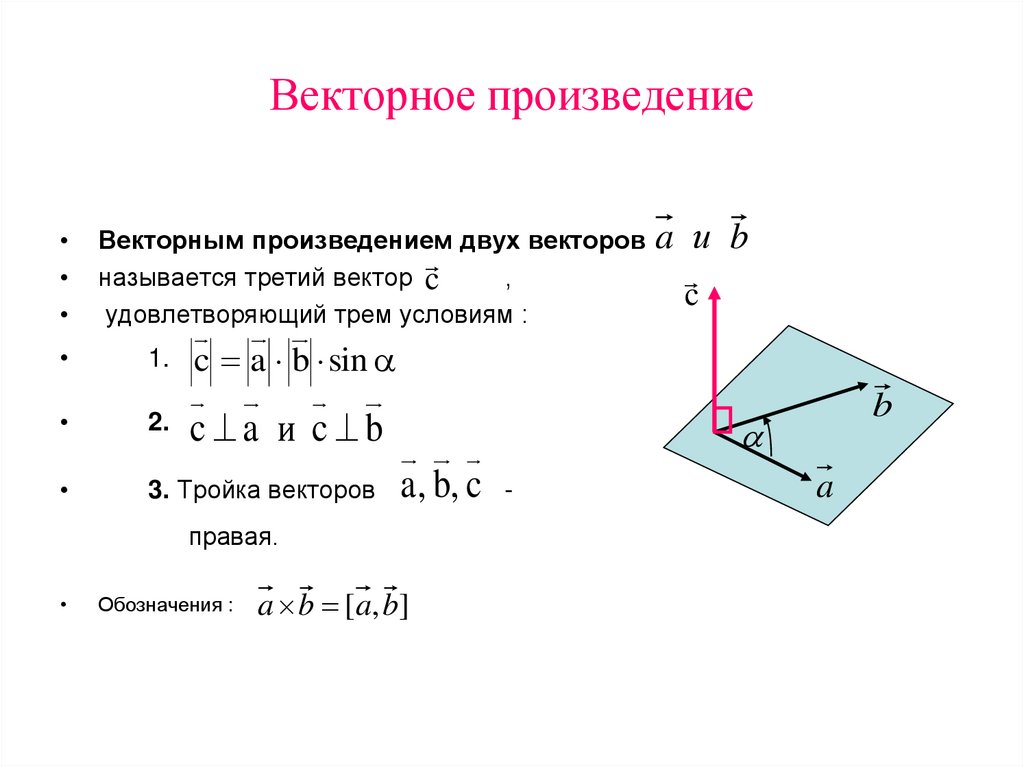
Векторным произведением двух векторов
называется третий вектор c
,
удовлетворяющий трем условиям :
c
c a b sin
1.
2.
3. Тройка векторов
c a и c b
Обозначения :
b
a, b, c
правая.
a и b
a b [ a, b]
-
a

19. Физический смысл векторного произведения

Пусть к твердому телу,
закрепленному в точке А,
приложена в точке В сила
M A (F )
А
В
F
F
Момент силы F , приложенной
в точке В, относительно точки А
равен векторному произведению
вектора
AB
и силы
F
M A ( F ) AB F
:

20. Векторное произведение

• Свойства векторного произведения.
• 1. a b b a
• 2. ( a ) b (a b)
• 3. a (b c) a b a c
• 4. Геометрический смысл .
Модуль векторного произведения двух векторов
численно равен площади параллелограмма,
построенного на этих векторах:
a b S
b
a

21.

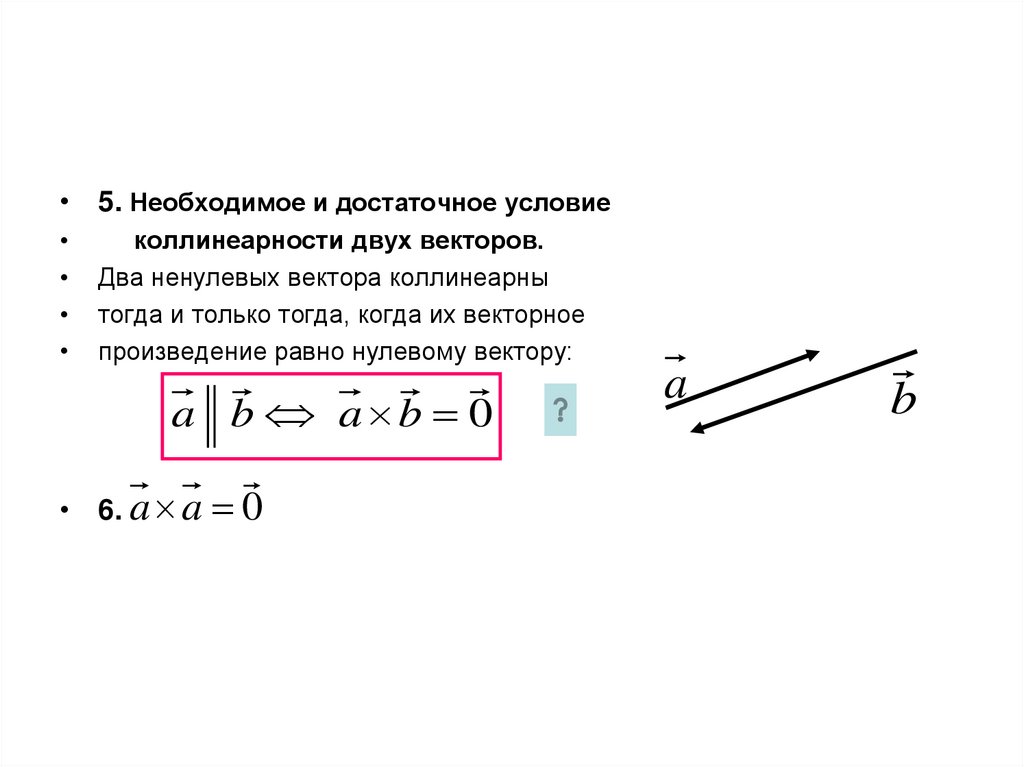
• 5. Необходимое и достаточное условие
коллинеарности двух векторов.
Два ненулевых вектора коллинеарны
тогда и только тогда, когда их векторное
произведение равно нулевому вектору:
a b a b 0
• 6. a a
0
a
b

22.

23. Векторное произведение ортов

Найдем векторное произведение ортов
координатных осей. Докажем, что
i , j, k
z
i j k
k
i k, j k
а)
б) векторы i , j, k образуют правую
тройку, значит i j || k,
в) | i j | 1, значит i j k.
Аналогично доказывается, что j k i ,
и k i j.
i
x
0
j
y

24. Векторное произведение

• Векторное произведение векторов,
• заданных в координатной форме.
Пусть
Тогда
a x1 , y1 , z1 и b x2 , y2 , z 2
i j k
a b x1 y1 z1
x2 y2 z2
y1 z1
x1 z1
x1 y1
a b y z i x z j x y k
2 2
2 2
2 2

25.

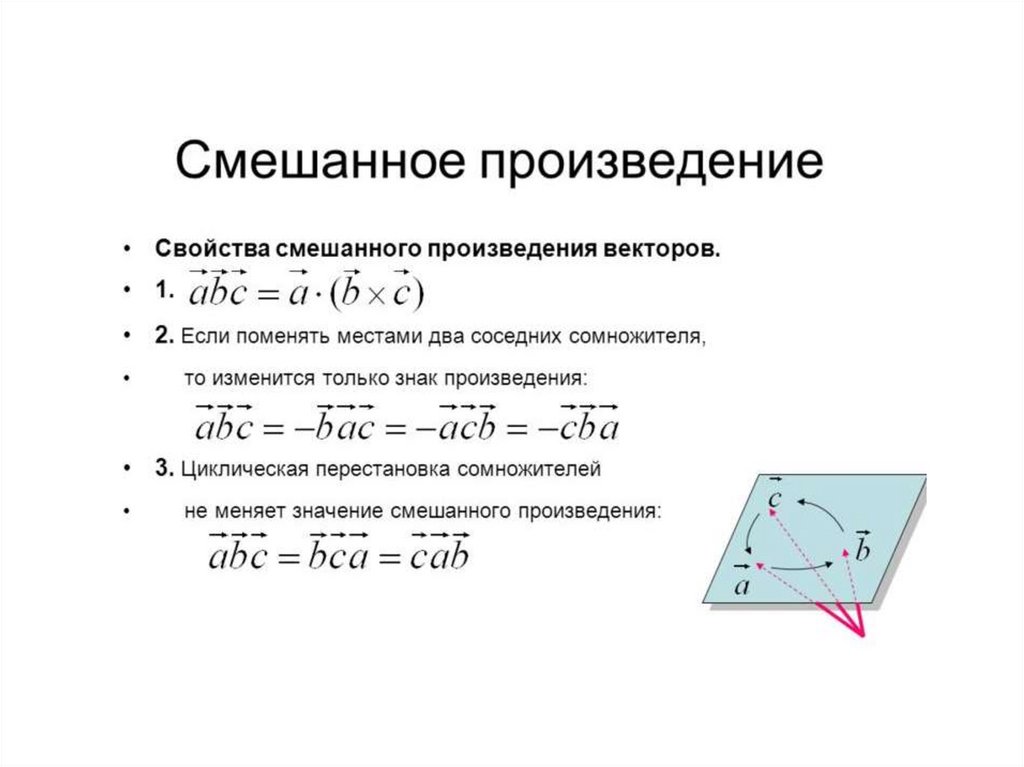
26. Смешанное произведение

• Определение.
Смешанным произведением трех векторов
называется векторное произведение первых двух
векторов, умноженное скалярно на третий вектор:
abc ( a b) c
a b c ( a , b, c )
Обозначения:
Замечание.
Результат смешанного произведения трех векторов
является скалярной величиной.

27.

28. Смешанное произведение

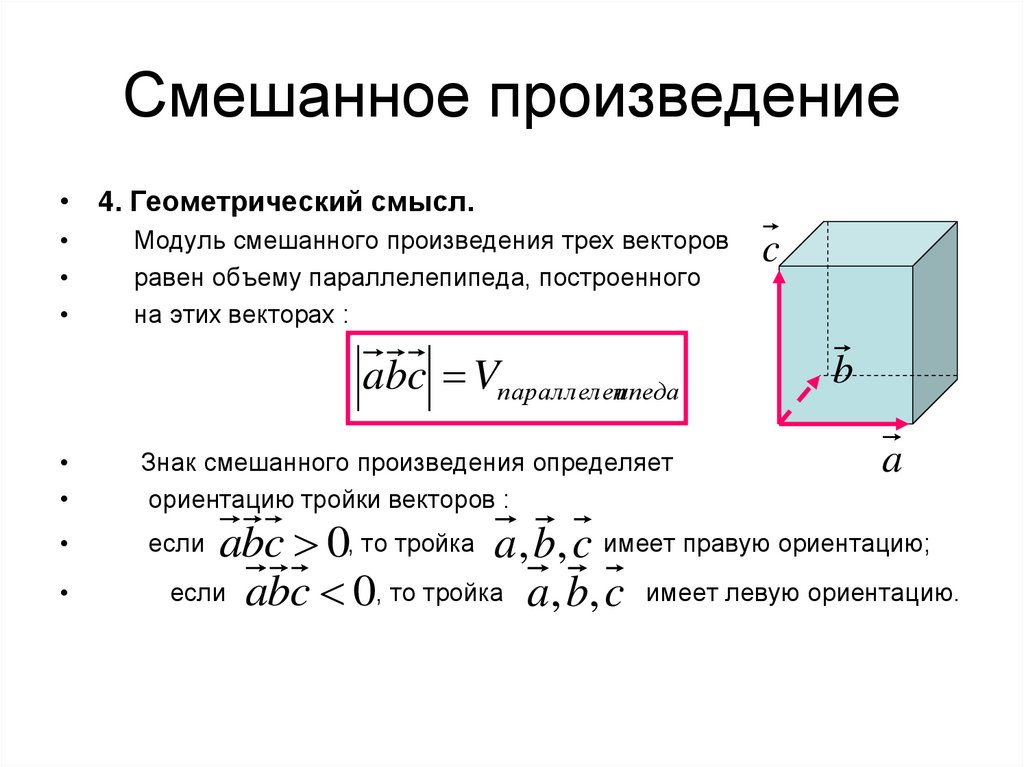
• 4. Геометрический смысл.
Модуль смешанного произведения трех векторов
равен объему параллелепипеда, построенного
на этих векторах :
abc Vпараллелепипеда
Знак смешанного произведения определяет
ориентацию тройки векторов :
если
c
b
a
abc 0, то тройка a, b, c имеет правую ориентацию;
если abc 0, то тройка a , b, c имеет левую ориентацию.

29. Смешанное произведение

• 5. Необходимое и достаточное условие
компланарности трех векторов.
Три ненулевых вектора компланарны
тогда и только тогда, когда смешанное
произведение этих векторов равно нулю.
Д.з.
Доказать
самостоятельно,
используя
геометрический смысл
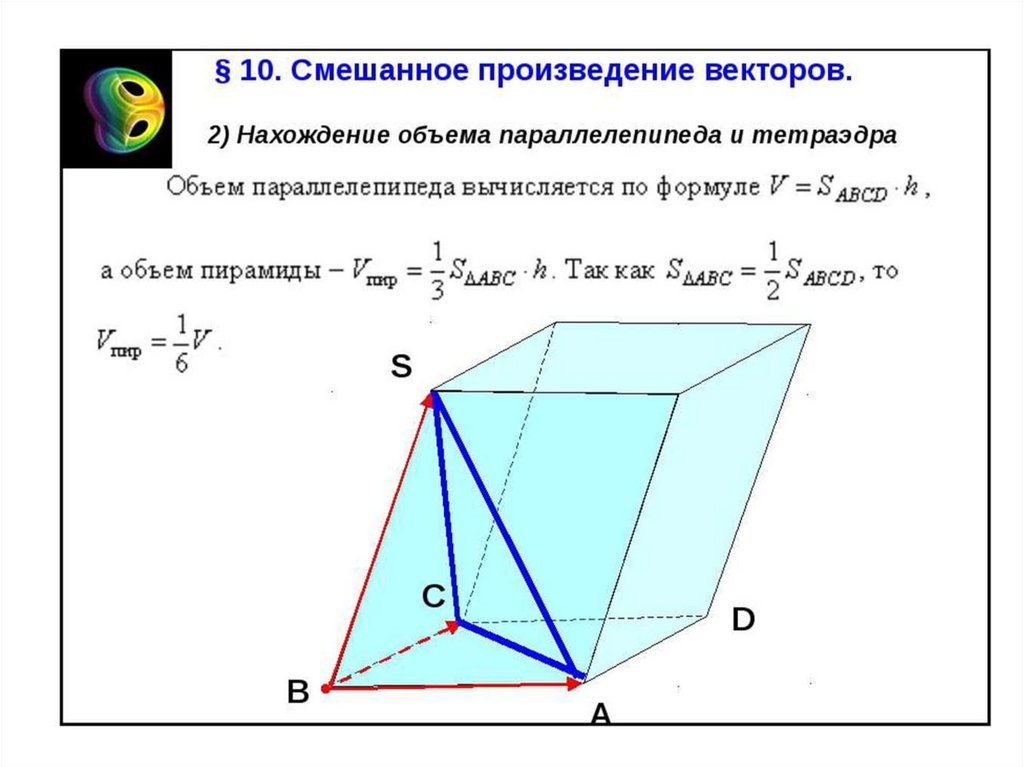
Смешанное произведение векторов,
заданных в координатной форме.
Пусть
a x1 , y1 , z1
b x2 , y2 , z2
c x3 , y3 , z3
Тогда
x1 y1 z1
abc x2 y2 z2
x3 y3 z3