Основы векторной алгебры

1. ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ

2. 1. Векторы на плоскости и в пространстве

1. ВЕКТОРЫ НА ПЛОСКОСТИ И В
ПРОСТРАНСТВЕ

3.

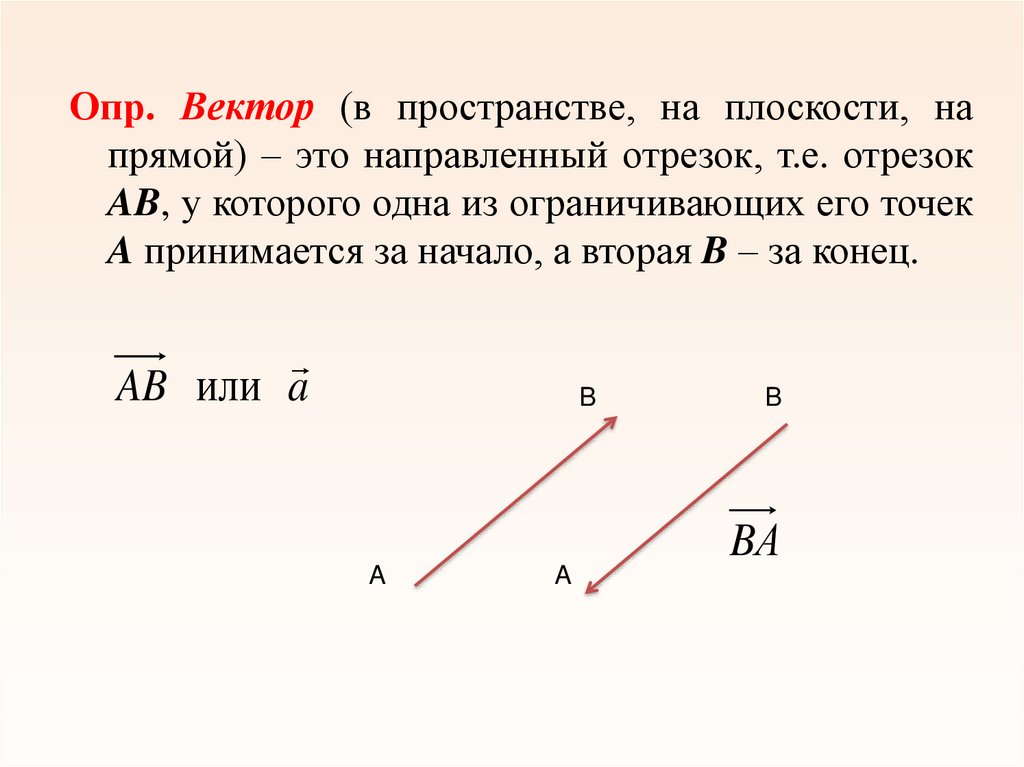
Опр. Вектор (в пространстве, на плоскости, на
прямой) – это направленный отрезок, т.е. отрезок
AB, у которого одна из ограничивающих его точек
A принимается за начало, а вторая B – за конец.
AB или a
B
B
BА
A
A

4.

Опр. Ненулевые векторы AB и CD называются
равными: AB CD , если:
1)
они лежат на одной прямой или на
параллельных прямых;
2)
имеют одинаковые длины ( AB CD) и
одинаково направлены.
Все нулевые векторы считаются равными друг другу.
B
A
C
D

5.

Операции над векторами

6. Сложение векторов

• Пусть а и b - два произвольных вектора. Возьмем
произвольную точку О и приложим вектор к этой точке,
получим а ОA .
• Затем отложим от точки А вектор b , получим
b АB .
а
ОB
Вектор
называется суммой векторов и b .
ОА AB OB
а
b
а
О
а
b
а
А
b
а b
b
b
с
B
Правило параллелограмма
Правило треугольника
с а b

7. 2. Разность векторов

Опр. Разность векторов а и b обозначается а b
определяется как сумма вектора
противоположного вектора b.
а
а
b
О
А
b
с
с а b
B
а
и
и

8. 3. Умножение вектора на число

Опр. Произведение вектора а на число называется вектор,
длина которого равна числу а
и который имеет
направление вектора а , если 0, и противоположное
направление ( а ), если 0.
Обозначается: а .
Если 0 или а 0 , то а 0 .
а
3а
2а

9.

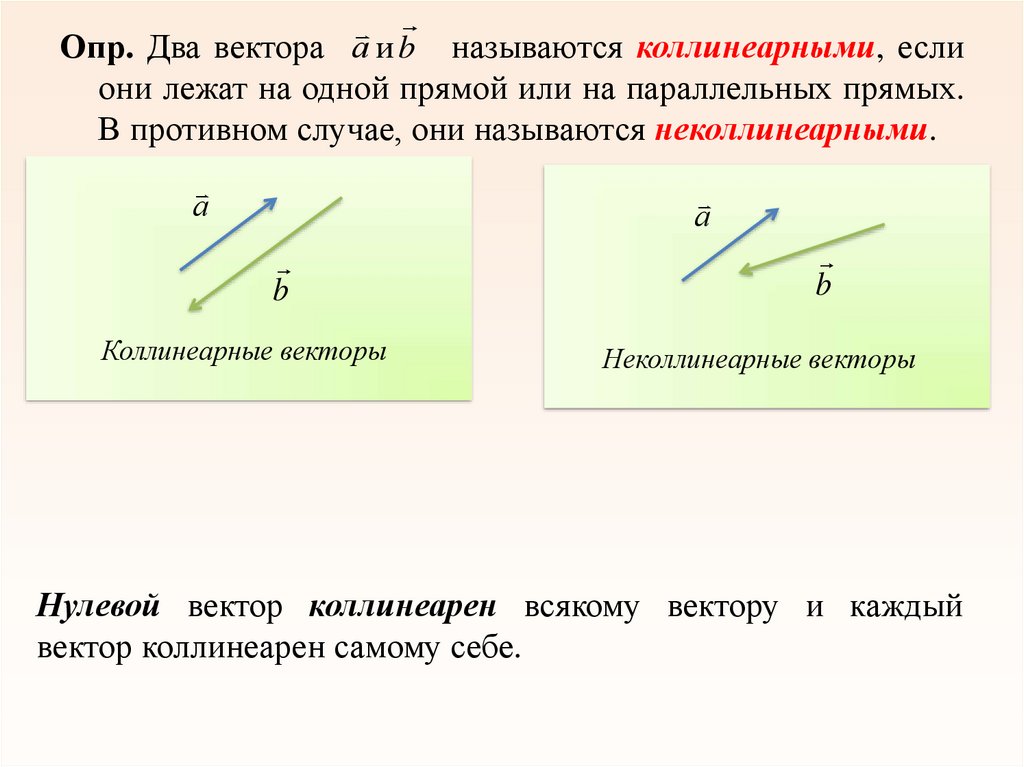
Опр. Два вектора а и b называются коллинеарными, если
они лежат на одной прямой или на параллельных прямых.
В противном случае, они называются неколлинеарными.
а
а
b
Коллинеарные векторы
b
Неколлинеарные векторы
Нулевой вектор коллинеарен всякому вектору и каждый
вектор коллинеарен самому себе.

10.

Опр. Три вектора а , b и с называются компланарными, если
они лежат на одной плоскости или на параллельных
плоскостях. В противном случае, они называются
некомпланарными.
Если хоть один из векторов а , b и с
нулевой вектор, то эти
векторы компланарны.
с
b
а
Компланарные векторы
с
b
а
Некомпланарные векторы

11. ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ

12.

z
y
k
j
i
O
x
i
j
O
x
• О – произвольная точка
• i , j i , j , k единичные взаимно-перпендикулярные векторы плоскости
(пространства) – орты
• Oxy – прямоугольная система координат на плоскости
• Oxyz – декартовая система координат в пространстве
• x – абсцисса
• y – ордината
• z – аппликата
y

13.

Вектор a заданный на плоскости Oxy,
y
y1
j
O
A(x1, y1)
a
i
x1
x
может быть представлен в виде:
a x1i y1 j
где x1, y1 – проекции вектора на
соответствующие оси координат
называются прямоугольными
координатами вектора.
a x1; y1

14.

Если даны координаты его начальной и конечной
точек.
А( x1; y1; z1 ) и B( x2 ; y2 ; z2 ).
AB x2 x1; y2 y1; z2 z1 .

15. Условие коллинеарности двух векторов

a x1 , y1 , z1 и b x2 , y2 , z 2
Векторы
коллинеарны тогда и только тогда, когда их
соответствующие координаты
пропорциональны, т.е. когда справедливо
равенство
x1 y1 z1
x2 y 2 z 2

16.

Длина вектора a x , y
1 1
в прямоугольных координатах :
2
2
a x1 y1
Длина вектора a x , y , z в декартовых координатах:
1 1 1
a x12 y12 z12

17. Линейные операции над векторами в координатной форме

Если
a x1 , y1 , z1 и b x2 , y2 , z 2
Тогда
a b x1 x2 ; y1 y2 ; z1 z 2
a x1 ; y1 ; z1

18. Пример

a 2; 6; 5 b 1; 3; 4 c 4; 1; 2
Найти :
а)2a 3b c

19. СКАЛЯРНОЕ И ВЕКТОРНОЕ ПРОИЗВЕДЕНИЯ ВЕКТОРОВ

20.

Опр. Скалярным произведением двух векторов
a иb
называется число, обозначаемое a b и равное
a b a b cos( a, b )
Если a x1 , y1 , z1 , b x2 , y2 , z 2
a b x1 x2 y1 y2 z1 z 2
a b
cos( a , b )
ab
a x1 x2 x3
2
2
2

21.

Пример
.
a 2; 6; 5 b 1; 3; 4
Найти :
а)a b
б) a
в ) cos( a; b )

22.

Три некомпланарных вектора a , b , c образуют
правую тройку (левую тройку) или положительно
ориентированы (отрицательно
ориентированы),
если с конца третьего вектора c кратчайший
поворот от первого вектора a ко второму b виден
против часовой стрелки (по часовой стрелке).
c
b
a
Правая тройка
c
a
b
Левая тройка

23. Векторное произведение векторов

Опр. Векторным произведением двух
векторов a и b
называется такой третий вектор с , который
удовлетворяет следующим
трем
условиям:
1) вектор ортогонален c a и c b
2) с a b sin( a , b )
3) векторы a , b , c образуют правую тройку.

24. Обозначения:

c a b или c [a , b ]
c
b
a

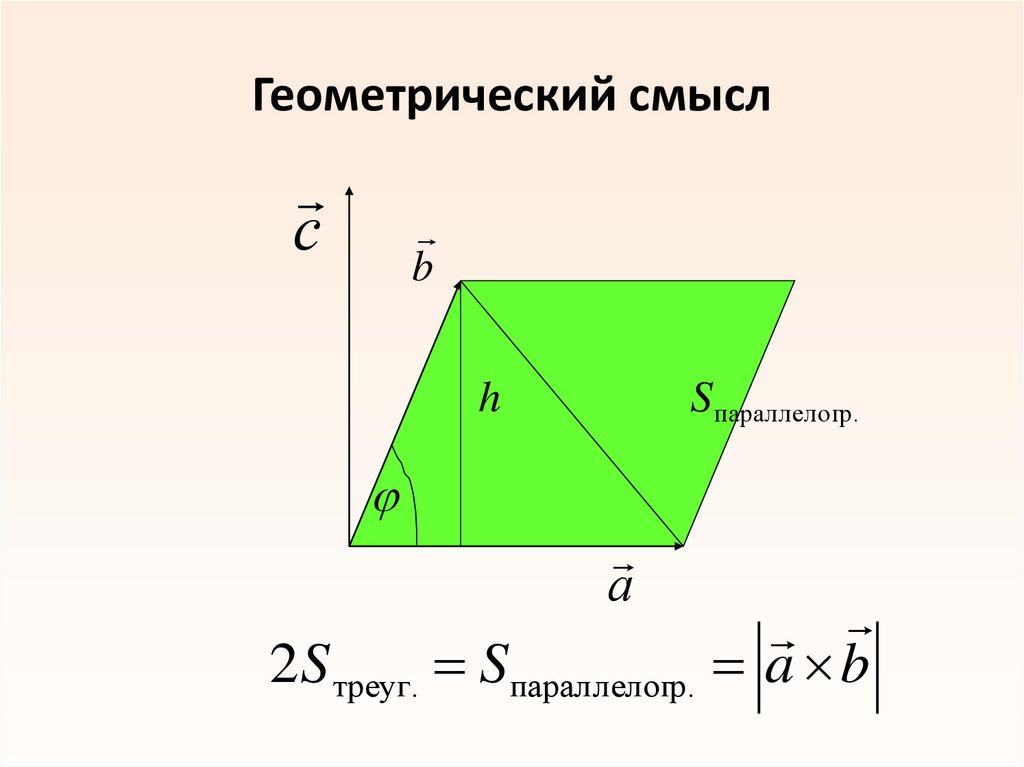
25. Геометрический смысл

с
b
h
S параллелогр.
а
2S треуг. Sпараллелогр. a b

26. 6. Теорема (запись векторного произведения в координатах)

Если a x1 , y1 , z1 и b x2 , y2 , z 2
i
j k
c a b x1 y1 z1 c1 ; c2 ; c3
x2 y 2 z 2
y1
c1
y2
z1
z1
, c2
z2
z2
x1
x1
, c3
x2
x2
y1
y2

27. Пример

a 2; 6; 5 b 1; 3; 4
Найти :
а)a b

28. Смешанное произведение векторов

Опр. Смешанным
произведением
трех
векторов a , b , c
называется
число,
обозначаемое a b c и определяемое
следующим образом
abc = (a × b) c
Другие обозначения :
(a , b, c), a , b, c .

29. Геометрический смысл

a bc
b
a
Vпарал. (a b ) c

30. 7. Теорема (запись смешанного произведения в координатах)

Если
a x1 , y1 , z1 ,
b x2 , y2 , z 2 ,
c x3 , y3 , z3 ,
тогда
x1
a b c x2
x3
y1
y2
y3
z1
z2 .
z3

31. 8. Признак компланарности трех векторов (линейной зависимости трех векторов) Векторы компланарны (линейно зависимы)

8. Признак компланарности трех векторов
(линейной зависимости трех векторов)
Векторы a , b , c компланарны
(линейно зависимы)
ab c 0
x1
x2
x3
y1
y2
y3
z1
z2 0
z3