Похожие презентации:
Векторная алгебра
1. Векторная алгебра
Скалярноепроизведение векторов
Векторное произведение векторов
Смешанное произведение векторов
2. Скалярное произведение векторов
Определение скалярного произведения векторовСвойства скалярного произведения векторов
Скалярное произведение векторов в
координатной форме
Условие перпендикулярности векторов
Нахождение угла между векторами
Физическое приложение скалярного
произведения векторов
3. Определение скалярного произведения векторов
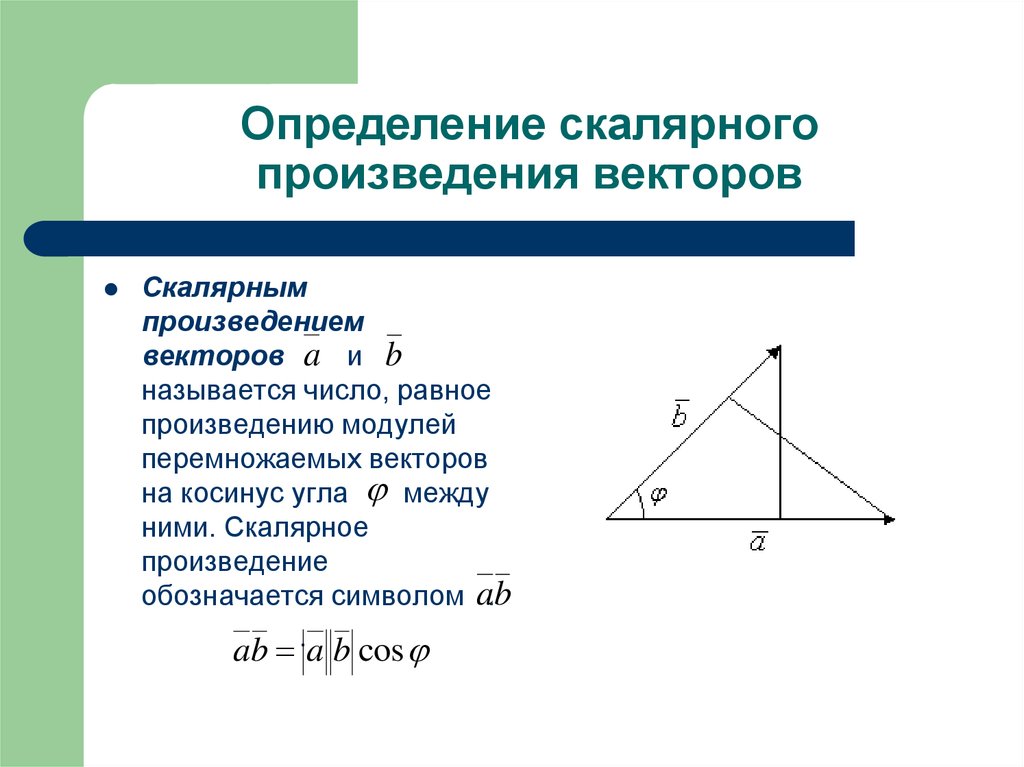
Скалярнымпроизведением
векторов a и b
называется число, равное
произведению модулей
перемножаемых векторов
на косинус угла между
ними. Скалярное
произведение
обозначается символом a.b
.
ab a b cos
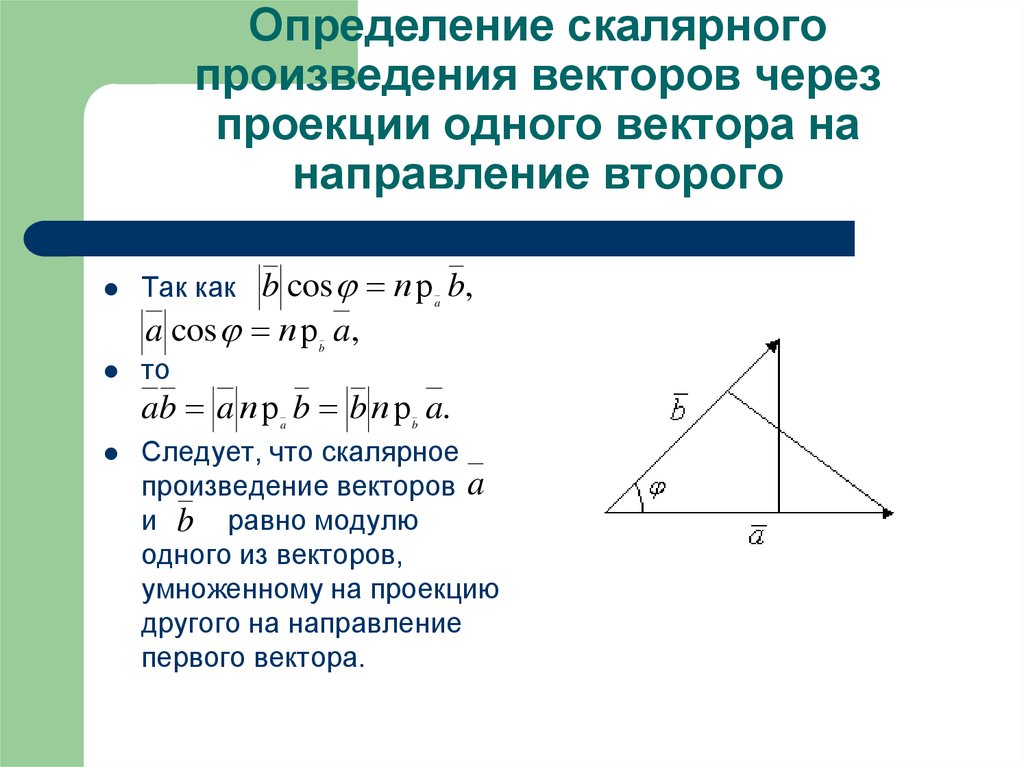
4. Определение скалярного произведения векторов через проекции одного вектора на направление второго
Так как b cos п р b,a
a cos п р a,
b
то
ab a п р b b п р a.
a
b
Следует, что скалярное
произведение векторов a
и b равно модулю
одного из векторов,
умноженному на проекцию
другого на направление
первого вектора.
5. Свойства скалярного произведения векторов
1) a b b a;2) ab 0 , если a b или хотя бы один из
векторов есть нулевой вектор
(справедливо и обратное утверждение);
3) a a a ;
4) (ab) ( a)b a( b)
для R;
5) a b c a c b c.
2
6. Скалярное произведение векторов в координатной форме
Пусть векторы a и b заданы своими координатами:a x i y j z k , b x i y j z k.
1
1
1
2
2
2
Найдем скалярное произведение a b . Вычислим
предварительно скалярные произведения
единичных векторов.
Имеем ii i i cos 0 1 1 1 1, j j 1, k k 1.
Векторы i, j, k взаимно перпендикулярны. Тогда,
согласно свойству 2, их произведения друг на друга
равны нулю. Итак, ab x x y y z z .
1
2
1
2
1
2
7. Условие перпендикулярности векторов
Следствие 1. Если ,2
то ab 0
Условие x x y y z z 0
называется условием
перпендикулярности двух
векторов, если векторы a и
b заданы своими координатами:
a x i y j z k , b x i y j z k.
1
1
1
2
1
1
2
1
2
2
2
2
8. Нахождение угла между векторами
Пусть векторы a и bзаданы своими координатами:
a x i y j z k,
1
1
b x i y j z k.
1
2
2
2
Следствие 2.
Так как ab a b cos , то
ab
xx y y zz
cos
,
ab
x y z x y z
1
2
2
1
1
2
1
2
1
2
1
2
2
2
2
2
2
2
9. Физическое приложение скалярного произведения векторов
ПРИМЕР Вычислить работу по перемещениюматериальной точки вдоль отрезка, из точки
B(1; 2;3) в точку С (3;4;2) под действием
постоянной по величине и направлению силы
F 2;1;5 .
Решение. Из курса физики известно, что работа,
совершаемая при указанных в примере условиях,
находится по формуле
A F S F BC.
Так как , BC 2;6; 1 , F 2;1;5
то A F BC 2 2 1 6 5 ( 1) 5.
Ответ: 5.
10. Векторное произведение векторов
Определение векторного произведения векторовСвойства векторного произведения векторов
Векторное произведение векторов, заданных
своими координатами
Физическое приложение векторного
произведения векторов
Геометрическое приложение векторного
произведения векторов
11. Определение векторного произведения векторов
ОПРЕДЕЛЕНИЕ Векторным произведениемвектора a на вектор b называется вектор c ,
удовлетворяющий условиям:
1) длина вектора c численно равна площади
параллелограмма, построенного на векторах a и b
как на сторонах, т.е. c a b sin a , b ;
2) вектор c перпендикулярен обоим векторам a и b ;
3) вектор c направлен в ту сторону, что если смотреть
из его конца вдоль вектора, то кратчайший поворот
вектора а к b вектору виден совершающимся против
движения часовой стрелки. Векторное произведение
векторов обозначаемся символом a b .
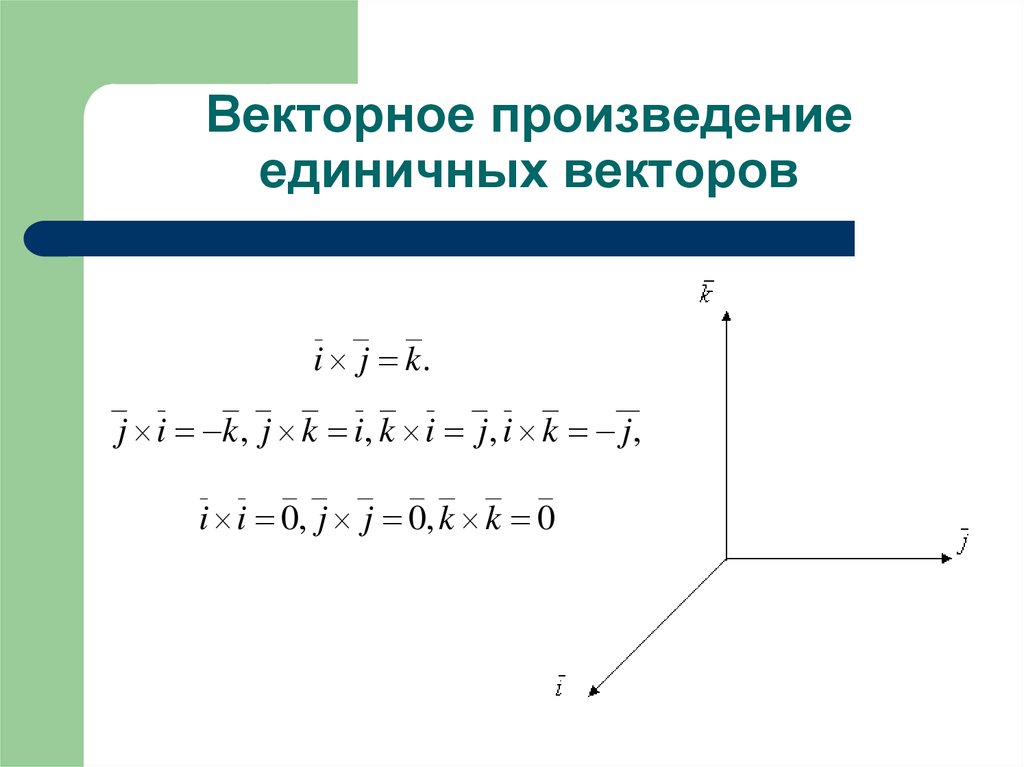
12. Векторное произведение единичных векторов
i j k.j i k , j k i, k i j , i k j ,
i i 0, j j 0, k k 0
13. Свойства векторного произведения векторов
a b b a ;a b a b a b для
a a 0;
a b 0 , если
R;
a b или хотя бы один
из векторов есть нулевой вектор;
a b c a b a c.
14. Векторное произведение векторов, заданных своими координатами
Пусть a x ; y ; z , b x ; y ; z . Тогда, согласносвойствам 2,3,4 получим
1
a b
y
1
y
2
z
1
z
2
1
1
i
x
1
x
i
j
k
a b x
y
1
z
x
y
2
z
1
2
1
2
2
2
z
1
z
2
j
2
x
1
x
2
2
y
1
y
2
i
j
k
k x
1
y
1
z.
x
2
y
2
z
1
2
15. Физическое приложение векторного произведения векторов
F 3;2; 4ПРИМЕР Сила
приложена к точке
Определить момент силы относительно начала координат.
A
R
M (2; 1;1) .
3
Решение. Пусть точка
есть некоторая точка
. Моментом силы
F , приложенной к точке M , относительно точки A называется вектор
По
AM F .
AM OM 2; 1;1 , F 3;2; 4 .
условию
Тогда,
формуле, получим
i
OM F 2
Ответ:
2;11;7 .
3
j
1
2
k
1 2i 11 j 7 k .
4
согласно
16. Применение векторного произведения векторов в геометрии
ПРИМЕР Даны вершины треугольника A(1;2;0), B(3;0; 3) иC(5;2;6). Вычислить площадь этого треугольника.
AB, AC . Имеем:
AB 2; 2; 3 , AC 4;0;6 .
Так
как
равен
площади
параллелограмма
AB AC
y
z
x
z
x
y
d c ( a b )c
x
y
z .
y
z
x
z
x
y
Решение. Найдем векторы
1
1
1
1
3
2
1
1
3
2
2
3
2
2
2
, то площадь S треугольника ABC найдется по формуле
i
S
1
2
1
1
AB AC
| 2
2
2
4
12 ( 24) 8
Ответ: 14
2
2
2
j
k
2
0
1
2
3 |
6
1
12i 24
2
874 14.
17. Смешанное произведение
Определение смешанного произведениявекторов
Смешанное произведение векторов, заданных
своими координатами
Геометрический смысл смешанного
произведения трех векторов
Условие компланарности трех векторов
Вычисление объема треугольной пирамиды
18. Определение смешанного произведения векторов
Пусть даны три вектора a, b, c .Смешанное произведение, т.е. произведение, в котором
вначале находится векторное произведение двух из
заданных векторов, затем скалярное произведение
полученного вектора на третий из данных векторов.
Например, вначале находится векторное произведение
a b d, затем - скалярное произведение d c (a b) c .
Смешанное или иначе векторно-скалярное произведение
обозначается символом (a b) c или символом abc .
Результатом смешанного произведения является число.
19. Смешанное произведение векторов, заданных своими координатами
Пусть требуется определить смешанное произведениевекторов, если известны координаты этих векторов
a x ; y ; z , b x ; y ; z , c x ; y ; z
Вычислим предварительно a b d . Имеем
1
Найдем
1
1
2
i
j
k
d a b x1
y1
z1
x2
y2
z2
d c ( a b )c
y
1
y
2
2
2
y1
z1
y2
z2
z
1
z
i
x
3
2
3
x1
z1
x2
z2
x
z
1
x
2
Полученное равенство, согласно
теореме о разложении определителя
по элементам строки, можно переписать
в форме
1
z
3
j
x1
y1
x2
y2
y
3
2
3
k.
x
y
x
y
1
2
1
z.
3
2
x
1
y
1
z
2
y
2
z
2
y
3
z
3
a b c x
x
3
1
20.
Правая и левая тройки векторов всмешанном произведении
векторов
Для смешанного
произведения
векторов
справедливы
равенства
c
a
a b c b c a c a b
a c b c b a b a c
c
a
+
b
_
b
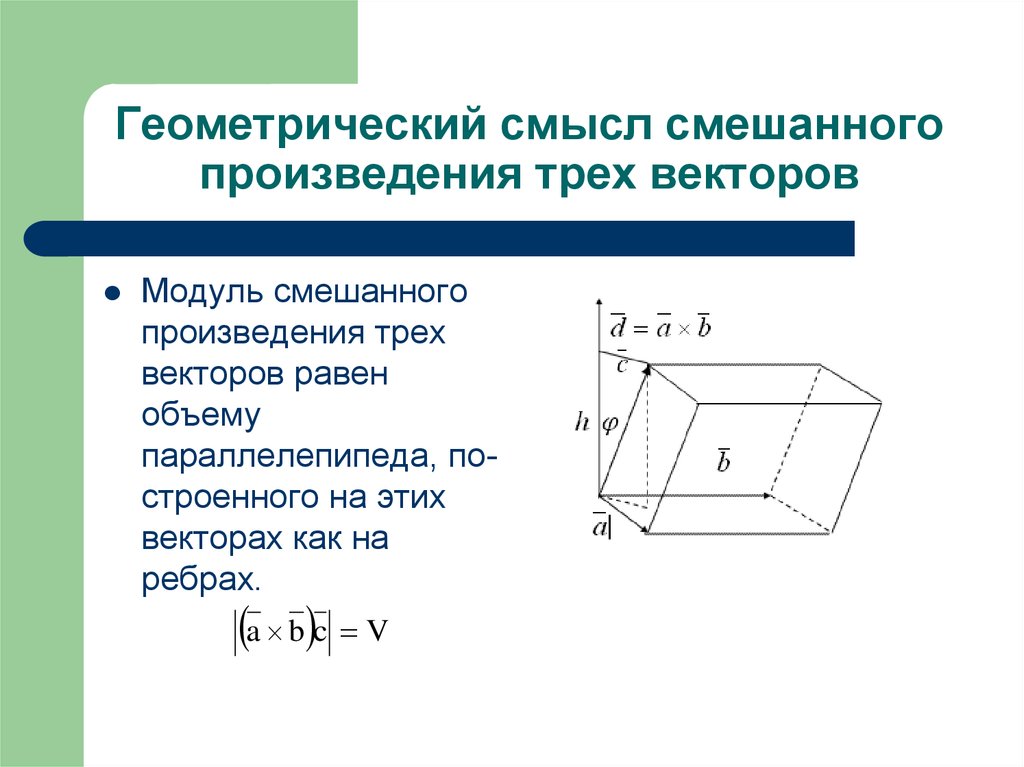
21. Геометрический смысл смешанного произведения трех векторов
Модуль смешанногопроизведения трех
векторов равен
объему
параллелепипеда, построенного на этих
векторах как на
ребрах.
a b c V
22. Условие компланарности трех векторов
Для того, чтобы три вектора a, b, c быликомпланарны, необходимо и достаточно,
чтобы их смешанное произведение
a b c 0 или в
равнялось нулю, т.е.
координатной форме
x
y
1
z
x
y
2
z 0
y
3
z
1
2
x
3
1
2
3
23. Вычисление объема треугольной пирамиды
ПРИМЕР Вычислить объем треугольной пирамиды с вершинами вточках A(2; 1;1), B(5;5;4), C(3;2; 1), D(4;1;3).
Решение. Построим три вектора
AB 3;6;3 , AC 1;3; 2 , AD 2;2;2 с общим началом точкой A . На
этих векторах, как на ребрах, построим параллелепипед. Его объем равен
AB AC AD .
Объем пирамиды V составляет шестую долю объема
параллелепипеда. Следовательно,
3 6
3
1 2
1
1
2
1
1
1
V AB AC AD | 1 3 2 | | 1 3 2 | | 1 3 2 |
6
6
2 2 2
1 1 1
0 1 0
|
1
1
1 2
| 3 3.
Ответ: 3



















 Математика
Математика








