Матрицы

1.

Лектор - Демина Елена Леонидовна,
доцент, кандидат физ.-мат.наук

2.

3.

В основу презентации положено пособие
Демин С.Е., Демина Е.Л.
«Линейная алгебра». Нижний Тагил : НТИ (ф) УГТУ-УПИ, 2015.
http://elar.urfu.ru/handle/10995/32053
http://moodle.ntiustu.ru

4.

Линейная алгебра
• Определители второго порядка
• Системы из двух линейных уравнений с двумя
неизвестными
• Определители n – ого порядка
• Методы вычисления определителей
• Системы из n линейных уравнений с n
неизвестными. Формулы Крамера
• Матрицы. Основные понятия
• Действия над матрицами

5.

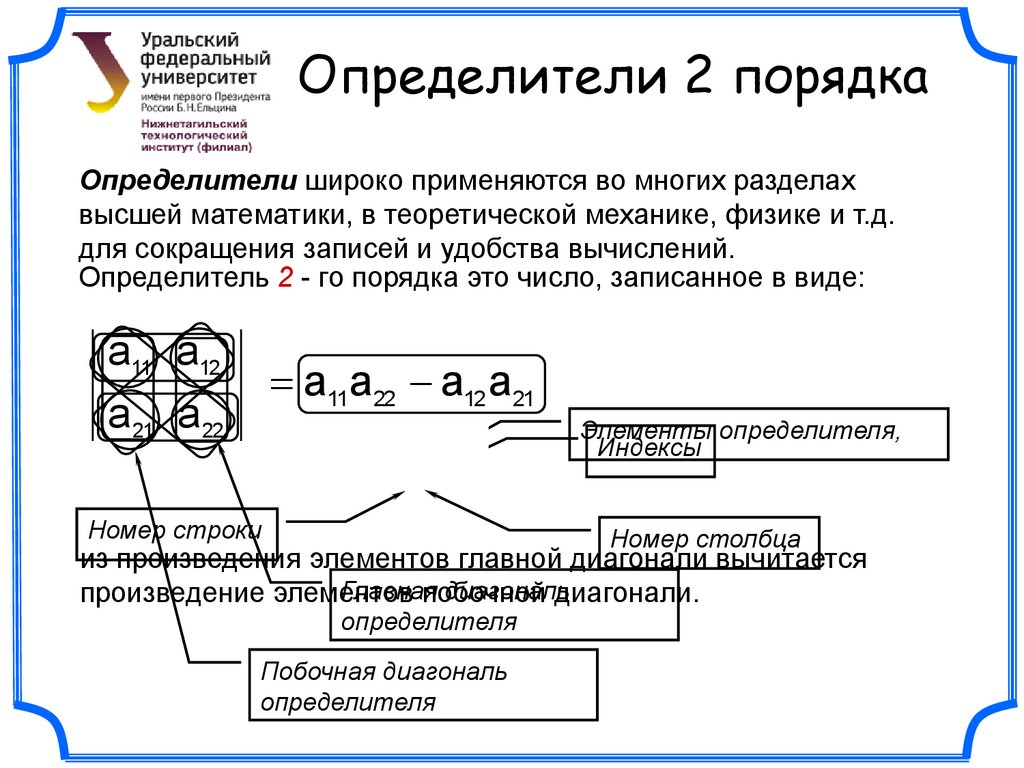
Определители 2 порядка
Определители широко применяются во многих разделах
высшей математики, в теоретической механике, физике и т.д.
для сокращения записей и удобства вычислений.
Определитель 2 - го порядка это число, записанное в виде:
a11 a12
a11a22 a12 a21
a 21 a 22
ai j
Номер строки
Элементы определителя,
Индексы
Номер столбца
из произведения элементов главной диагонали вычитается
Главная
диагональ
произведение элементов
побочной
диагонали.
определителя
Побочная диагональ
определителя

6.

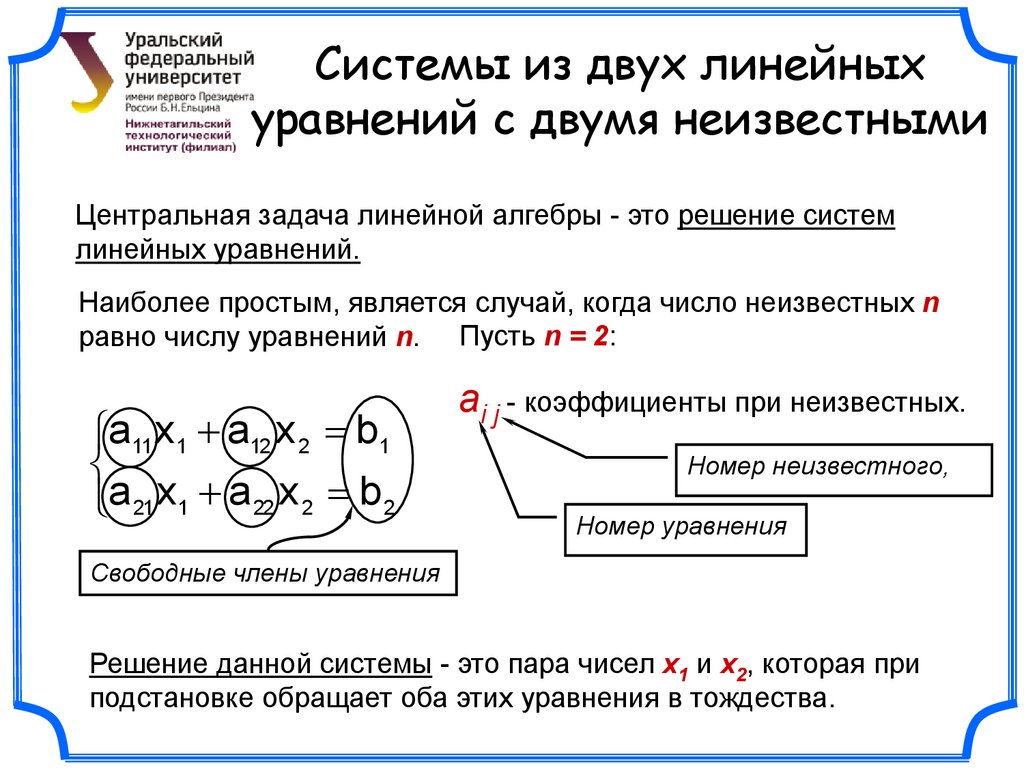
Системы из двух линейных
уравнений с двумя неизвестными
Центральная задача линейной алгебры - это решение систем
линейных уравнений.
Наиболее простым, является случай, когда число неизвестных n
равно числу уравнений n. Пусть n = 2:
a11 x1 a12 x 2 b1
a 21 x1 a 22 x 2 b 2
ai j - коэффициенты при неизвестных.
Номер неизвестного,
Номер уравнения
Свободные члены уравнения
Решение данной системы - это пара чисел х1 и х2, которая при
подстановке обращает оба этих уравнения в тождества.

7.

Системы из двух линейных
уравнений с двумя неизвестными
a11 x1 a12 x 2 b1
a 21 x1 a 22 x 2 b 2
a11 a 22 x1 a12 a 22 x 2 b1 a 22
a12 a 21 x1 a12 a 22 x 2 a12 b 2
a
11
a22 a12 a21 x1 a22 b1 a12 b2
Обозначим:
1
b1 a12
b 2 a 22
a11 a12
a 21 a 22
a11 a22 a12 a21
b1 a 22 a12 b 2
x1 1

8.

Системы из двух линейных
уравнений с двумя неизвестными
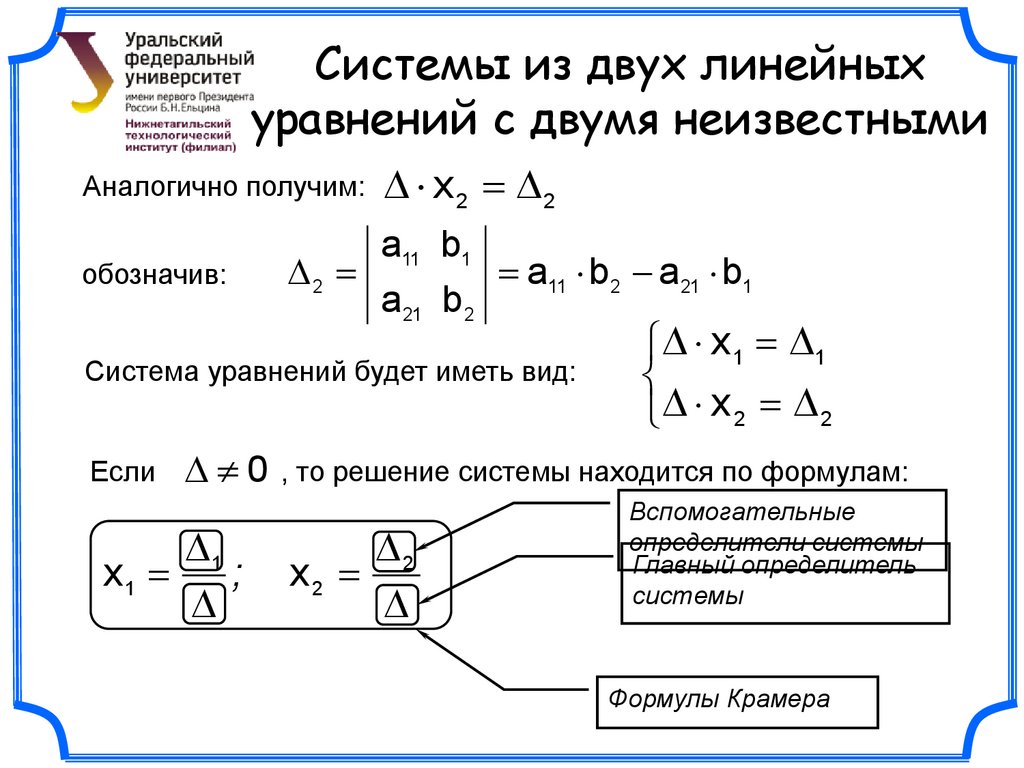
Аналогично получим:
обозначив:
2
x2 2
a11 b1
a 21 b 2
a11 b 2 a 21 b1
Система уравнений будет иметь вид:
Если
0
1
x1
;
x 1 1
x 2 2
, то решение системы находится по формулам:
2
x2
Вспомогательные
определители системы
Главный определитель
системы
Формулы Крамера

9.

Системы из двух линейных
уравнений с двумя неизвестными
1
x1
;
2
x2
Формулы Крамера
Габриэ́ль Кра́мер
1704— 1752
швейцарский математик, один из
создателей линейной алгебры.

10.

Системы из двух линейных
уравнений с двумя неизвестными
Решить систему методом Крамера:
2x1 x 2 5
3 x1 2x 2 3
Вычислим главный и вспомогательные определители системы:
21
51
5 2 3 1 7
2 2 3 1 1 0 1
3 2
32
2 5
2
2 3 3 5 9
3 3
Найдем решение системы по формулам Крамера:
7
x 1 7;
1
9
x2
9
1

11.

Определители n – ого порядка
Определителем n – ого порядка называется число:
a11 a12
a 21 a 22
an1 an 2
a1n
a 2n
ann
Методы вычисления определителей n – ого порядка рассмотрим
на примере вычисления определителей третьего порядка.

12.

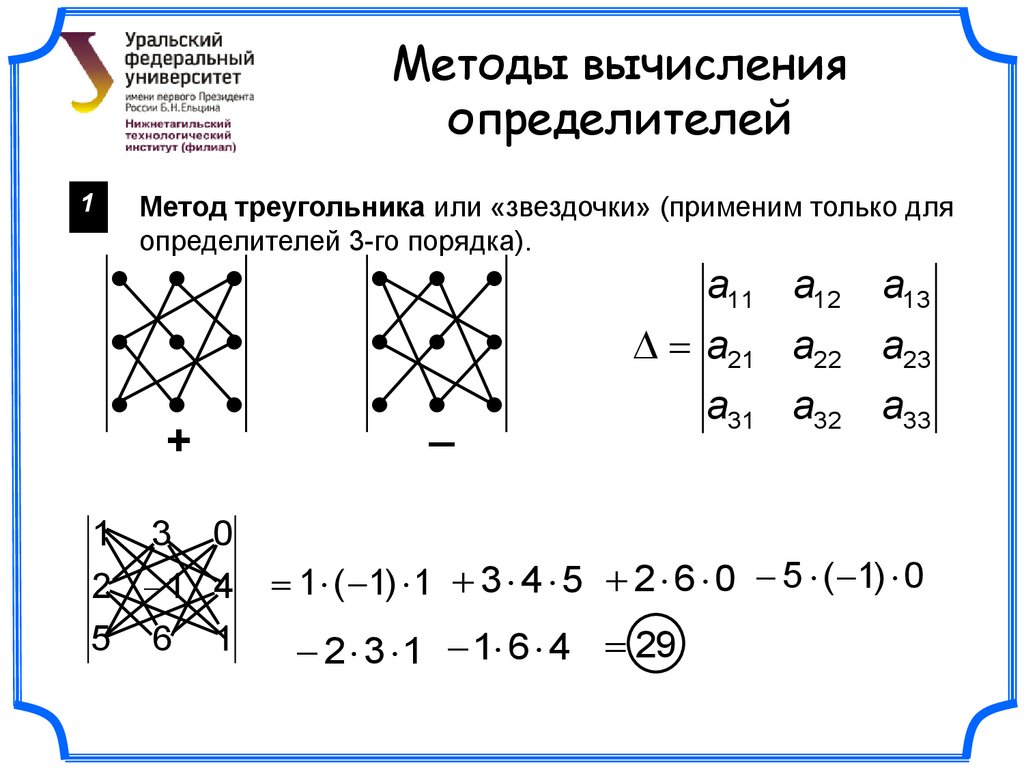
Методы вычисления
определителей
1
Метод треугольника или «звездочки» (применим только для
определителей 3-го порядка).
+
1 3 0
2 1 4
5 6 1
_
a11 a12 a13
a21 a22 a23
a31 a32 a33
1 ( 1) 1 3 4 5 2 6 0 5 ( 1) 0
2 3 1 1 6 4 29

13.

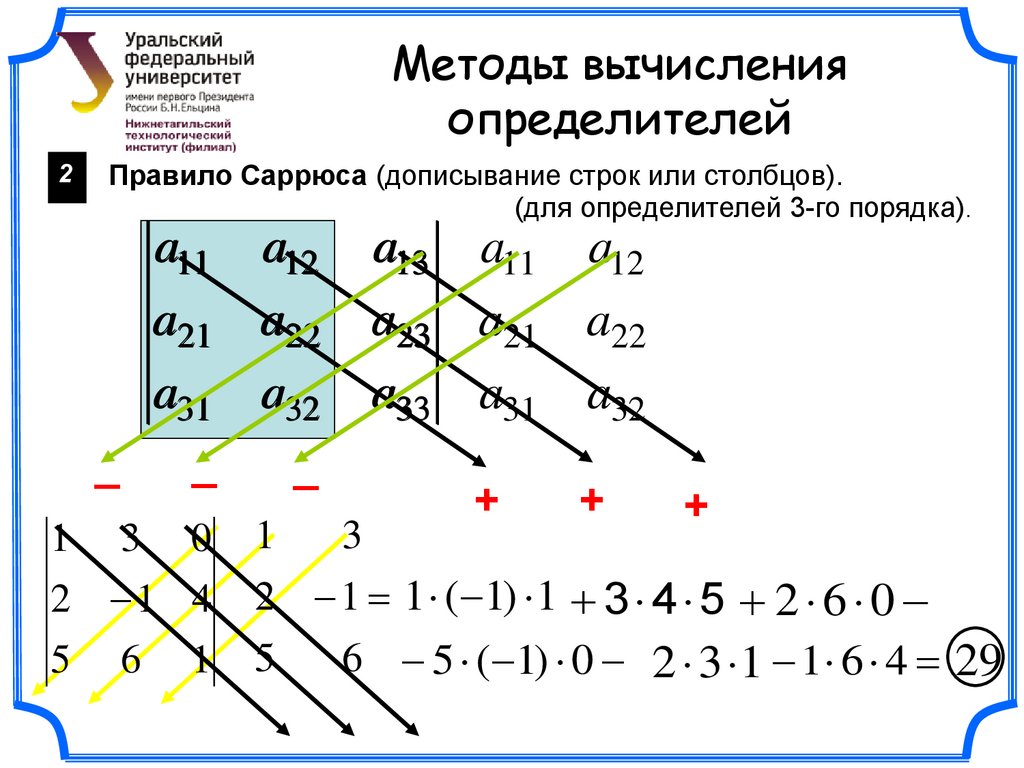
Методы вычисления
определителей
2
Правило Саррюса (дописывание строк или столбцов).
(для определителей 3-го порядка).
a11 a12
a21 a22
a31 a32
_
_
1 3 0
2 1 4
5 6 1
_
a13 a11 a12
a23 a21 a22
a33 a31 a32
+
+
+
1
3
2 1 1 ( 1) 1 3 4 5 2 6 0
5
6 5 ( 1) 0 2 3 1 1 6 4 29

14.

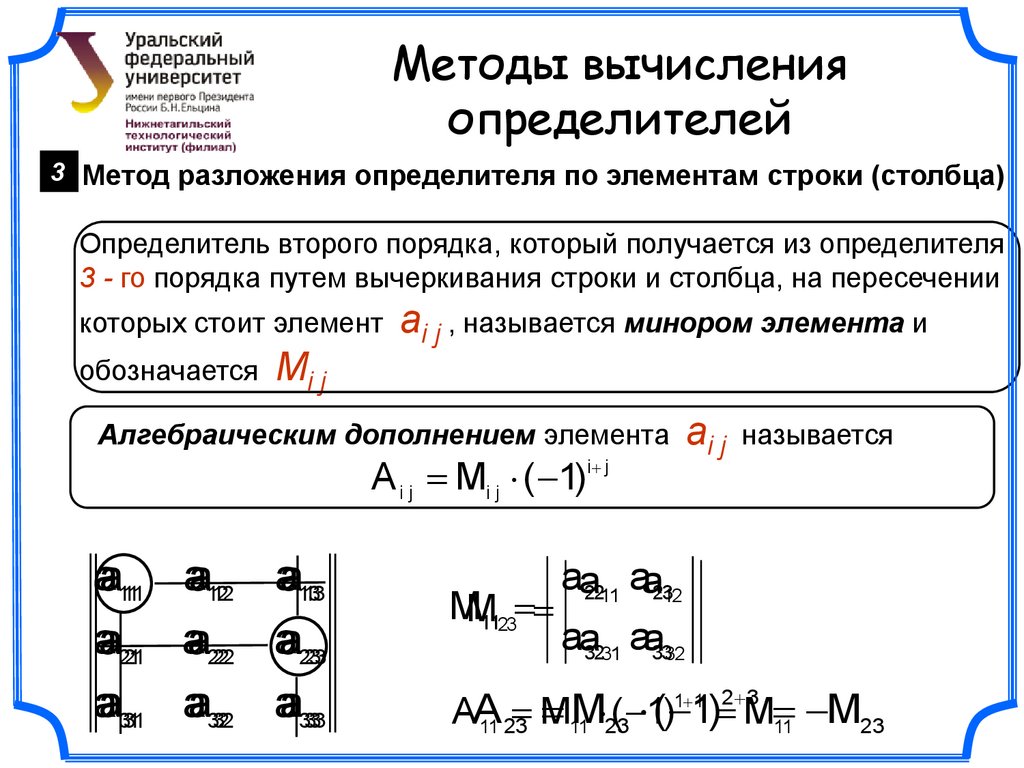
Методы вычисления
определителей
3 Метод разложения определителя по элементам строки (столбца)
Определитель второго порядка, который получается из определителя
3 - го порядка путем вычеркивания строки и столбца, на пересечении
которых стоит элемент
обозначается
ai j , называется минором элемента и
Mi j
ai j
Алгебраическим дополнением элемента
A i j Mi j ( 1)i j
aa1111 aa1212 aa1313
aa2121 aa2222 aa2323
aa3131 aa3232 aa3333
называется
aa2211 aa2312
MM1123
aa3231 aa3332
11M 23( 1() 1) M
M23
AA
M
11 23
11
1 1 2 3

15.

Методы вычисления
определителей
Величина определителя равна сумме произведений элементов
какой – либо строки (столбца) определителя на их
алгебраические дополнения:
n
ai j A i j
Разложение определителя по элементам
i – ой строки
ai j A i j
Разложение определителя по элементам
j – ого столбца
j 1
n
i 1
2 1 0
0 1
0 3
3 1
1 2
1 1
0 3 1 2
( 1) 0
( 1)1 3
( 1) 1
2 1
2 5
5 1
2 5 1
2 (3 1 5 1) 1 (0 1 2 1) 2

16.

Методы вычисления
определителей
4
Использование свойств определителя
Свойства определителя (доказать самостоятельно):
Величина определителя:
равна нулю, если элементы какого - либо столбца или строки
равны нулю:
0 0
0
a21 a22
равна нулю, если соответствующие элементы двух строк
(столбцов) равны
a11 a12
a11 a12
0

17.

Методы вычисления
определителей
меняет знак, если поменять местами строки (столбцы):
a11 a12
a21 a22
a12 a11
a22 a21
увеличивается в k раз, если элементы какого - либо столбца
(строки) увеличить в k раз:
k a11 k a12
a21
a22
k
a11 a12
a21 a22
не меняется при замене строк соответствующими столбцами:
(эта операция называется транспонированием)
a11 a12
a 21 a 22
a11 a 21
a12 a 22

18.

Методы вычисления
определителей
не меняется, если к элементам какой-либо строки (столбца)
прибавить соответствующие элементы другой строки (столбца),
умноженные на произвольный множитель
Если определитель имеет так называемый треугольный вид,
то он вычисляется как произведение чисел, стоящих на
главной диагонали:
a11 a12 a13
0 a22 a23 a11a22 a33
0 0 a33

19.

Методы вычисления
определителей
1 3 1
1
3 1 1 3 1
5 1
2 1 3 0 5 1 0 5 1 1
( 1)1 1
7 2
1 4 1
1 4 1 0 7 2
5 2 7 1 17
S 2 S 2 2 S1
S S S
3
1
3
Выберем 1
К элементам
2
Разложим
столбец
и
К элементам
3
строки
прибавим
определитель
по
превратим
второй
строки
прибавим
элементы 11строки,
элементам
столбца
и третий
элементы
1
строки
умноженные на (-2)
элементы в нули
Также, используя свойства, можно привести определитель к
треугольному виду и вычислить по последнему свойству.

20.

Системы из n линейных уравнений
с n неизвестными
Рассмотрим общую квадратную систему линейных уравнений:
a11 x1 a12 x 2 a1n x n b1
a 21 x1 a 22 x 2 a 2n x n b2
an1x1 an 2 x 2 ann x n bn
Система линейных уравнений называется совместной, если она
имеет решение и несовместной, если она не имеет решений.
Совместная система называется определенной, если она имеет
единственное решение и неопределенной, если она имеет
бесконечное множество решений.
Система называется однородной, если b1 b2 bn 0
Однородная система совместна, так как всегда имеет нулевое
решение.

21.

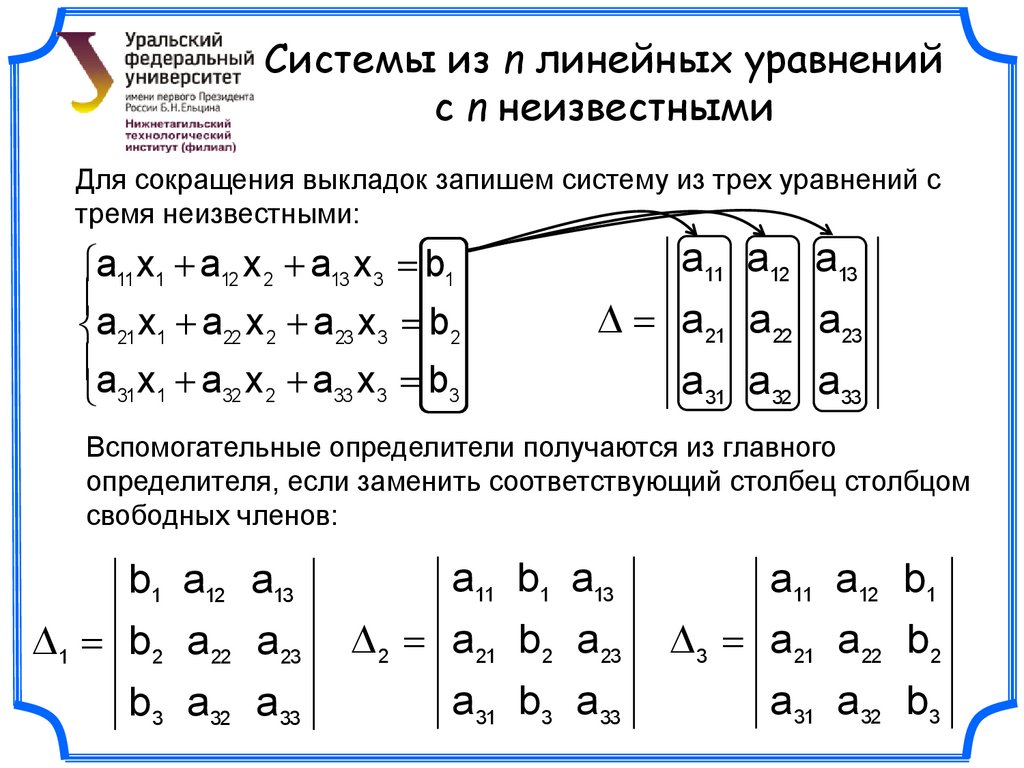
Системы из n линейных уравнений
с n неизвестными
Для сокращения выкладок запишем систему из трех уравнений с
тремя неизвестными:
a11 x1 a12 x 2 a13 x 3 b1
a21 x1 a22 x 2 a23 x 3 b2
a x a x a x b
33 3
3
31 1 32 2
a11 a12 a13
a 21 a 22 a 23
a31 a32 a33
Вспомогательные определители получаются из главного
определителя, если заменить соответствующий столбец столбцом
свободных членов:
b1 a12 a13
a11 b1 a13
a11 a12 b1
1 b 2 a 22 a 23
2 a 21 b 2 a 23
3 a 21 a 22 b 2
b3 a32 a33
a31 b3 a33
a31 a32 b3

22.

Системы из n линейных уравнений
с n неизвестными
По величине главного и вспомогательных определителей можно
судить о характере системы:
Если
0,
то система совместна и определенна.
Если 0,
1
неопределенна.
2 3 0, то система совместна и
Если 0, но 1 0 или
система несовместна.
2 0
или
3 0
то
В общем случае будем иметь n +1 определителей n – ого порядка
, 1, 2 , 3 , , n 2 , n 1, n
и, если 0 , то решение системы находится по формулам
Крамера:
1
x1 ;
2
x2
;
n
xn

23.

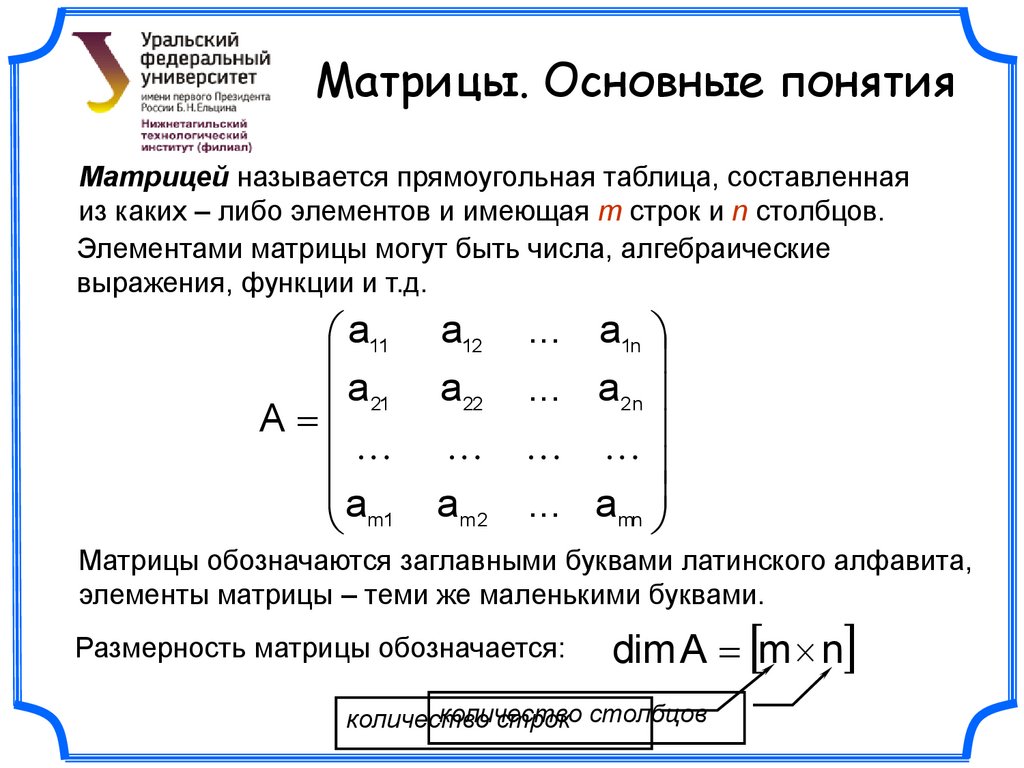
Матрицы. Основные понятия
Матрицей называется прямоугольная таблица, составленная
из каких – либо элементов и имеющая m строк и n столбцов.
Элементами матрицы могут быть числа, алгебраические
выражения, функции и т.д.
a11
a21
A
a
m1
a12 ... a1n
a 22 ... a2n
am 2 ... amn
Матрицы обозначаются заглавными буквами латинского алфавита,
элементы матрицы – теми же маленькими буквами.
Размерность матрицы обозначается:
dim A m n
количество
количество
строк столбцов

24.

Матрицы. Основные понятия
Если m n , то матрица называется прямоугольной.
Если m n
порядка).
, то матрица называется
квадратной (n - ного
Любое число (скаляр) можно представить как матрицу первого
порядка, размерностью 1 1 .
Матрица типа 1 n называется матрица-строка:
a
11
a12 a13 ... a1n
Матрица типа m 1 называется матрица-столбец:
a11
a 21
...
a
m1

25.

Матрицы. Основные понятия
Квадратная матрица называется единичной, если ее элементы,
расположенные на главной диагонали, равны единице,
остальные – нулю (обозначается буквой Е):
1 0 0
E 0 1 0
0 0 1
Если все элементы квадратной матрицы равны нулю, то она
называется нуль-матрицей и обозначается символом 0.
0 0 0
O 0 0 0
0 0 0

26.

Матрицы. Основные понятия
Для каждой квадратной матрицы n - ного порядка существует
определитель n - ного порядка, элементы которого равны
соответствующим элементам матрицы.
a11 a12
A a21 a22
a
31 a32
a13
a23
a33
a11 a12
det A a21 a22
a31 a32
a13
a23
a33
Определитель любой единичной матрицы равен единице.
Если определитель матрицы равен нулю, то
называется вырожденной, в противном случае
невырожденная.
матрица
матрица

27.

Действия над матрицами
Равенство матриц
A B
dim A dimB; aij bij
Сложение (вычитание) матриц
C A B
dim A dim B dim C
c ij aij bij
Умножение матрицы на число
B k A
dim A dimB; bij aij k

28.

Действия над матрицами
Найти значение выражения: C A 5 B
1 3 2
A
0 1 4
2 4 1
B
5 0 2
3 5 ( 4) 2 5 1 11 17 7
1 5 2
C
0 5 ( 5) 1 5 0 4 5 2 25 1 14

29.

Действия над матрицами
Умножение матриц
Произведение матриц A * B определено только тогда, когда
число столбцов матрицы А равно числу строк матрицы В, в
противном случае произведение не существует.
dim A m n
dim B n k
C A B существует
dimC m k
Произведением матрицы A размера [m n] с элементами aij на
матрицу B размера [n k ] с элементами bjq называется матрица C
размера [m k ] с элементами:
n
c iq aij b jq
j 1

30.

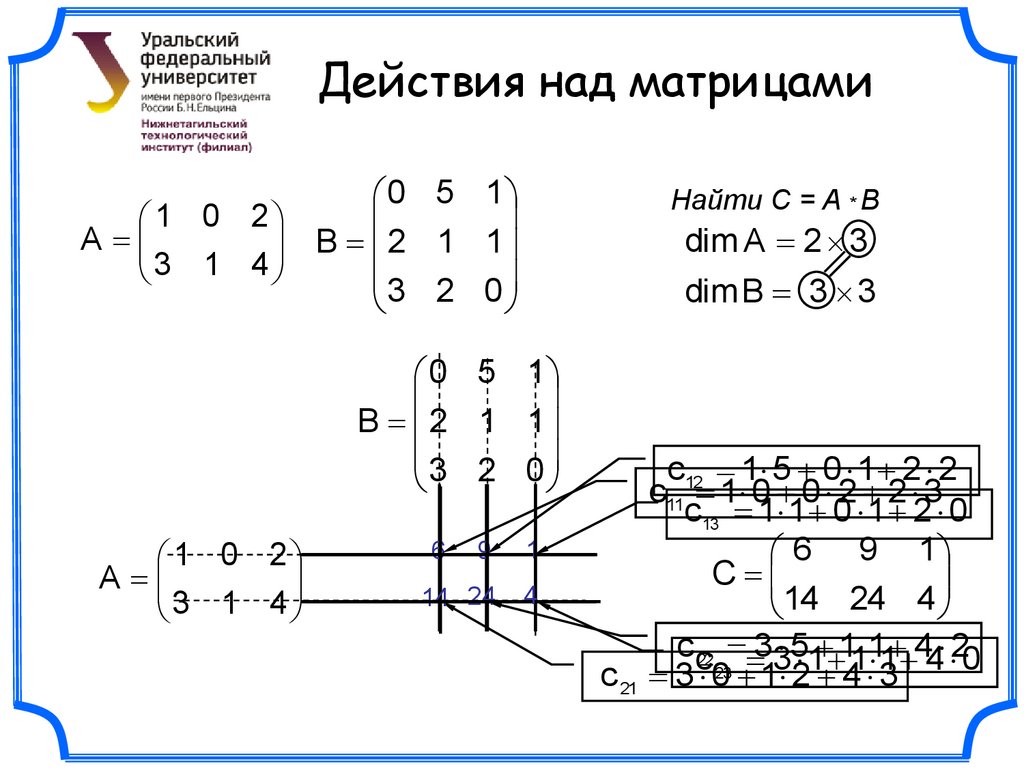
Действия над матрицами
1 0 2
A
3 1 4
0 5 1
B 2 1 1
3 2 0
Найти С = A * B
dim A 2 3
dim B 3 3
0 5 1
B 2 1 1
3 2 0
1 0 2
A
3 1 4
9
1
14 24
4
6
c12 1 5 0 1 2 2
c11 1 0 0 2 2 3
c 13 1 1 0 1 2 0
6 9 1
C
14 24 4
cc22 33 5 1 11 1
44 20
1
c 21 3 023 1 2 4 3

31.

Действия над матрицами
Свойства операции произведения матриц:
A BC AB C ;
2) AB A B ;
3) A B C AC BC ;
1)
4) В общем случае для произведения матриц не действует
переместительный закон: A B B A
иногда АВ существует, а ВА не имеет смысла. В случае, когда
АВ = ВА, матрицы А и В называются коммутативными.
5) Единичная матрица является коммутативной для любой
квадратной матрицы того же порядка:
EA AE A
6) Для двух квадратных матриц А и В одного порядка произведение
определителей равно определителю произведения .
det A det B det AB