Непрерывные функции и их свойства. Асимптоты

1. План-конспект практического занятия.

Тема: Непрерывные функции и их свойства. Асимптоты.
Цель: сформировать умения и навыки применения на практике
теоретического материала данного на лекции.
Задачи:
1)Образовательная
–
формирование
научного
мировоззрения.
2)Развивающая – развитие у обучающихся умения
обобщать, систематизировать полученные знания.
3)Воспитательные
–
воспитание
познавательного
интереса обучающихся, коммуникативных качеств,
умения
слушать,
культуры
межличностных
взаимоотношений, аккуратности в работе, трудолюбия.
Оборудование: Меловая
проектор.
доска,
компьютер,
мультимедийный

2.

№ Наименование
части
занятия
Содержание этапа
занятия (основные
понятия,
формулы, усло-вия
задач)
1
.
1) Определение
непрерывной
функции в точке?
Непреры
вность
функции
и точки
разрыва.
Основные
определе
ния
2) Определение
разрыва в точке?
Про
дол
жит
ельнос
ть
(ми
н.)
10
Ответы на теоретические вопросы данного этапа
занятия, подробное решение задач
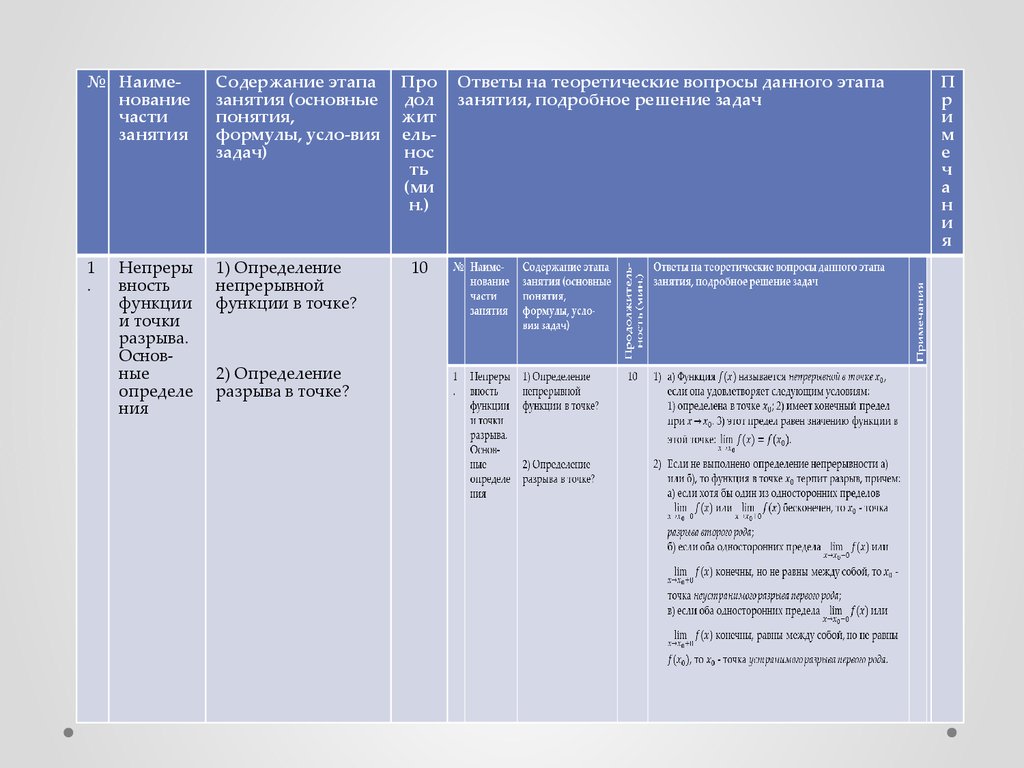
1) а) Функция называется непрерывной в точке , если она
удовлетворяет следующим условиям:
1)
определена в точке ; 2) имеет конечный предел при .
3) этот предел равен значению функции в этой точке: .
2) Если не выполнено определение непрерывности а)
или б), то функция в точке терпит разрыв, причем:
а) если хотя бы один из односторонних пределов
или бесконечен, то - точка разрыва второго рода;
б) если оба односторонних
предела или конечны, но не равны между собой, то точка неустранимого разрыва первого рода;
в) если оба односторонних предела или конечны,
равны между собой, но не равны , то - точка
устранимого разрыва первого рода.
П
р
и
м
е
ч
а
н
и
я

3.

2
Примеры
3) Исследовать на
непрерывность
функции в точке .
В случае разрыва
установить его
характер в точке .
a) ; Решение: При функция не определена,
следовательно, функция в точке терпит разрыв: т.е.
конечный предел существует; следовательно, – точка
устранимого разрыва 1-го рода. Доопределив
функцию в точке , т.е. положив , получим, что новая
функция
будет уже непрерывна в точке .

4.

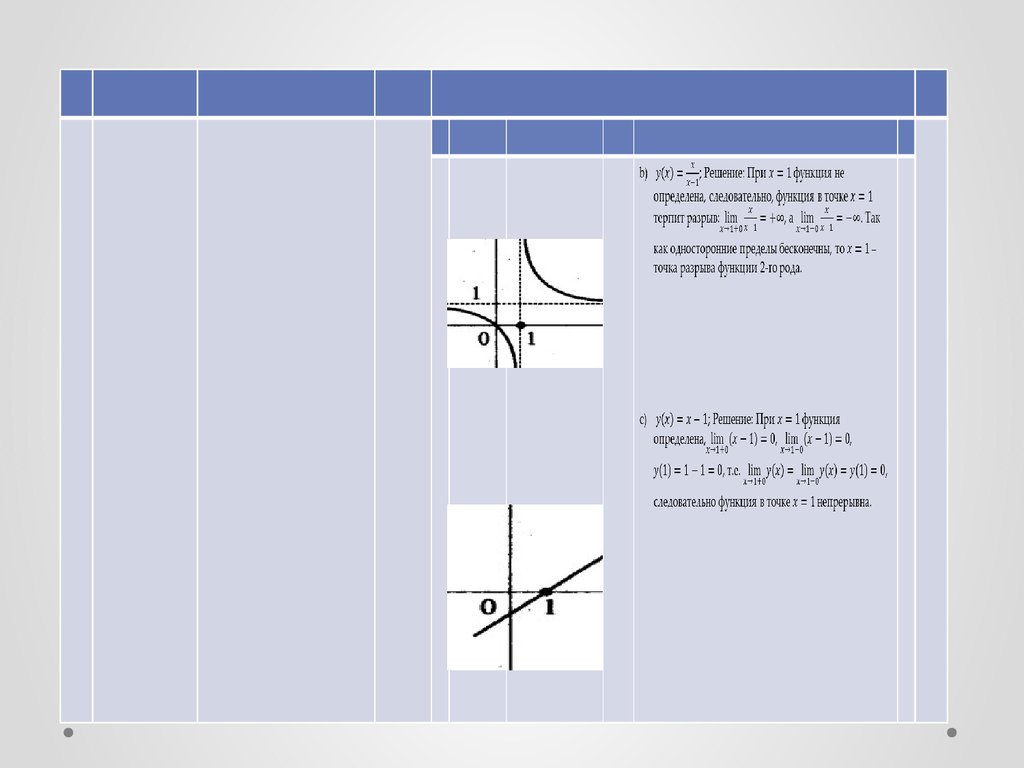
b) ; Решение: При функция не определена,
следовательно, функция в точке терпит разрыв:, а .
Так как односторонние пределы бесконечны, то –
точка разрыва функции 2-го рода.
c) ; Решение: При функция определена,, , , т.е. ,
следовательно функция в точке непрерывна.

5.

d) ; Решение: При функция определена, , , , имеем и
так как пределы конечны, то в точке функция терпит
неустранимый разрыв 1-го рода.

6.

4) Исследовать на
непрерывность и
найти точки
разрыва функции
y(x) и указать
характер разрыва.
4) Решение: При функция не определена. Для
установления характера разрыва в точке найдем
односторонние пределы при (слева) и при (справа):
при .
Таким образом, в точке функция имеет неустранимый
разрыв 1-го рода.

7.

3
Асимптоты.
Исследова
ние функций и
построение их
графиков.
Основные
определен
ия.
5) Определение
асимптоты и какие
их виды
существуют?
6) Определение
вертикальной
асимптоты?
10
5) Прямая называется асимптотой графика функции ,
если расстояние от точки до этой прямой стремиться
к нулю при неограниченном удалении точки графика
от начала координат. Асимптоты бывают
вертикальными, горизонтальны-ми и наклонными.
6) Прямая может быть, вертикальной асимптотой
функции в том случае, если - точка разрыва или
граничная точка области определения. Прямая
является вертикальной асимптотой графика
функции , если хотя бы один из пределов
(правосторонний или левосторонний).
7) Прямая является горизонтальной асимптотой, если . У
однозначной функции асимптот не существует.
7) Определение
горизонтальной
асимптоты?
8) Определение
наклонной
асимптоты?
8) Если и , то прямая является наклонной асимптотой
графика функции .

8.

4
Примеры
9) Исследовать
функцию y на
наличие асимптот.
1. ;
2.
3.
9) 1. ;
•) Область определения функции – .
•) Разрыв в точке ;
Отсюда прямая - вертикальная асимптота;
Отсюда прямая – горизонтальная асимптота.
Наклонных асимптот нет.
(
п
о
о
п
р
.)

9.

2.
• Область определения функции – .
• Функция непрерывна при всех действительных
значениях вертикальных асимптот нет.
• - горизонтальных асимптот нет.
Следовательно, наклонные асимптоты имеют вид:
3. .
• Область определения . Точки и – точки разрыва
функции.
• Для x=1:

10.

• Для
Отсюда прямые и – вертикальные асимптоты.
П
р
а
в
и
л
о
Л
о
п
и
т
а
л
я

11.

• . Прямая – горизонтальная асимптота.
Существует правило Лопиталя для раскрытия
неопределенности вида и :
Пусть функции и удовлетворяют следующим условиям:
1. эти функции дифференцируемы в окрестности точки
a, может быть и в самой точке a;
2. в этой окрестности;
3. или равны ;
4. существует конечный или бесконечный предел или ;
Тогда существует .
•. Наклонных асимптот нет.

12.

5
Домашнее
задание
10) Исследовать на
непрерывность,
найти точки
разрыва и указать
характер разрыва:
а)
б) ,
в) ,
2) Найти
асимптоты
графика функции:
а) ;
б) .
в) .