Лекции ТФКП

1.

ЛЕКЦИИ ТФКП

2.

1. КОМПЛЕКСНЫЕ ЧИСЛА И ДЕЙСТВИЯ НАД НИМИ
Комплексным числом z называется выражение вида
z x i y,
(1.1)
где x и y действительные числа, а i мнимая единица,
определяемая равенством i 2 1 или i 1 . Числа x и y
называются действительной и мнимой частями комплексного числа z
и обозначаются x Re z , y Im z .
Форму (1.1) комплексного числа z называют алгебраической.
Два комплексных числа z1 x1 iy1 и z 2 x 2 iy 2 считаются
равными, если равны их действительные и мнимые части: x1 x 2 ,
y1 y 2 . Число z равно 0 при условии x y 0 .
Понятия «больше» и «меньше» для комплексных чисел не
устанавливаются.

3.

Число z x iy называется сопряженным числу z x iy .
Алгебраические действия над комплексными
определяются следующими равенствами:
числами
z1 z 2 x1 iy1 x 2 iy 2 x1 x2 i y1 y 2 ,
z1 z 2 x1 iy1 x2 iy2 x1 x2 y1 y 2 i x1 y 2 x2 y1 ,
z1 z1 z 2 x1 x 2 y1 y 2 i x 2 y1 x1 y 2
z2 z2 z 2
x 22 y 22
Комплексное число z x iy изображается точкой M x, y на
координатной плоскости XOY (рис.1.1). При этом действительные
числа z x изображаются точками на оси OX , называемой здесь
действительной осью, а мнимые числа z iy изображаются точками
оси OY , называемой мнимой осью. Плоскость, на которой
изображают комплексные числа, называется комплексной
плоскостью.

4.

Комплексное число z x iy
может быть изображено вектором
r x, y с координатами x и y и с
началом в точке O 0,0 (рис.1.1).
Длина r r вектора r x, y ,
изображающего комплексное число
z, называется модулем комплексного
числа. Угол , образуемый этим
вектором
с
положительным
Рис.1.1
направлением действительной оси,
называется аргументом комплексного числа. Модуль числа принято обозначать r z , а аргумент
Arg z .
Для модуля и аргумента, как видно на рис.1.1, справедливы
формулы
r z x2 y2 ,
(1.2)
y
(при x 0 ).
(1.3)
tg
x

5.

Величина Arg z имеет бесконечное множество значений,
определяемых с точностью до целого кратного числа 2 . Если
величину одного из углов обозначить через 0 , то совокупность
величин всех углов запишется в виде:
Arg z 0 2 k
k 0, 1, 2,...
Значение Arg z , принадлежащее промежутку
называется главным и обозначается 0 arg z . Итак,
arg z ,
Arg z arg z 2k
k 0, 1, 2,. ..
, ,
(1.4)
(1.5)

6.

В силу формулы (1.3) и определения (1.4) находим, что
arctg
0 arg z arctg
arctg
y
,
x
y
,
x
y
,
x
для точек z из I и IV квадрантов ;
для точек z из II квадранта;
для точек z из III квадранта.
Если действительная часть x 0 , то 0
при y 0 , и
2
0 , при y 0 .
2
Комплексному числу 0 не приписывается какое-либо значение
аргумента.

7.

Зная модуль комплексного числа r z и его аргумента , мы можем
вычислить его действительную часть x и мнимую y:
x r cos ,
y r sin и записать число z в
форме
z r cos i sin
(1.6)
Эту форму комплексного числа называют тригонометрической.
Имеют место следующие правила умножения, деления,
возведения в целую положительную степень и извлечение корня для
чисел z в тригонометрической форме:
z1 z 2 r1 r2 cos 1 2 i sin 1 2 ,
z1 r1
cos 1 2 i sin 1 2 ,
z 2 r2
z n r n cos n i sin n , n N ,
2k
2k
n
z n r cos
i sin
,
n
n
где k 0,1,2,. .., n 1.
(1.7)
(1.8)
(1.9)
(1.10)

8.

Формула (1.9) при r 1 называется формулой Муавра.
Геометрически n значений выражения n z (1.10) изображаются
вершинами некоторого правильного n – угольника, вписанного в
окружность, с центром в начале координат и с радиусом n r .
Условимся выражение cos i sin обозначать символом e i ,
т.е.
(1.11)
e i cos i sin ,
не придавая этой записи пока никакого другого смысла, кроме как
обозначения. Далее будет показано, что символ e i обладает
свойствами показательной функции, для которой справедлива
формула (1.11), называемая формулой Эйлера.
Используя обозначение (1.11), умножив левую и правую части
на r, можно перейти от тригонометрической формы (1.6) к
показательной форме комплексного числа
z rei
(1.12)

9.

Ввиду
ее
компактности
она
удобнее
равносильной
тригонометрической формы.
Алгебраические действия (1.7) – (1.10) над комплексными
числами в показательной форме (1.12) имеют более рациональный
вид:
(1.13)
z1 z 2 r1r2 e i 1 2 ,
z1 r1 i 1 2
,
e
z 2 r2
(1.14)
z n r n e in ,
(1.15)
n
z n re
i
2 k
n
,
k 0,1,2, , n 1
(1.16)
При решении задач полезно помнить, что i 2 1, i 3 i , i 4 1,
i 5 i и т.д., и вообще при любом целом k i 4k 1 , i 4k 1 i , i 4k 2 1,
i 4k 3 i .

10.

1. Решить уравнение z 2 6 z 10 0 .
Решение. 1-й способ: D 36 40 4 .
6 4 6 2 1 6 2i
z1, 2
3 i , z1 3 i , z 2 3 i .
2
2
2
2-й способ: В результате подстановки z x iy в данное уравнение
2
имеем x iy 6 x iy 10 0 , откуда после преобразований
x 2 y 2 6 x 10 0
получим систему уравнений
. Решая систему,
xy 3 y 0
получим z1 x1 iy1 3 i , z 2 x2 iy 2 3 i .
3 2i
.
1 i
3 2i 1 i 3 2 2i 3i 5 i
5
Решение: z
, откуда Re z x ,
1 i 1 i
1 1
2
2
1
Im z y .
2
2. Найти Re z и Im z , если z

11.

1. Выяснить геометрический смысл модуля разности z1 z 2 двух
комплексных чисел z1 и z 2 .
Решение: z1 z 2 x1 x2 i y1 y 2 x1 x2 y1 y 2 .
Следовательно, z1 z 2 есть расстояние между точками z1 x1 iy1 ,
и z 2 x2 iy 2 (рис. 1.2).
2
Рис.1.2
2
Если изобразить комплексное
число с помощью вектора, то
действительная и мнимая части
z1 z 2
вектора
являются
координатами вектора, а так как при
вычитании векторов их координаты
соответственно вычитаются, то
вычитание комплексных чисел
сводится к вычитанию векторов, изображающих эти числа.
Как видно из рис. 1.2, z1 z 2 есть длина вектора z1 z 2 M 2 M 1 , т.е.
расстояние между точками, изображающими числа z1 и z 2 .

12.

1. Найти модуль и главное значение аргумента комплексного числа
z 1 3i , представить его в тригонометрической и показательной
формах.
Решение. По определению модуля r z x 2 y 2 1 3 2 . Так
как значения аргумента удовлетворяют соотношению
y
y 3
, то arg z arctg arctg 3 . Итак, z r 2 ,
tg
x
3
x
1
arg z и согласно (1.6) и (1.12) имеем z 2 cos i sin
3
3
3
, z 2e
i
3
.

13.

1. Для комплексных чисел z1 1 i и z 2 1 i 3 , вычислить z1 z2
и
z1
, представив их вначале в тригонометрической форме.
z2
3
3
Решение. z1 2 cos i sin , z 2 2 cos i sin .
3
3
4
4
Применяя формулы (1.7) и (1.8), получим
3
3
z1 z 2 2 2 cos i sin
3
3
4
4
5
5
2 2 cos i sin
12
12
z1
2 3
2 13
3
13
cos
i
sin
cos
i
sin
.
z2
2 4
3
3
2 12
4
12

14.

1. Вычислить 1 i 12 .
Решение. Запишем число z 1 i в тригонометрической форме. По
формуле (1.9) имеем 1 i
12
2
12
2 cos i sin
4
4
cos 3 i sin 3 2 6 1 i 0 64 .
12

15.

1. 7. Вычислить и изобразить на комплексной плоскости все значения
3
8.
Решение. Представим z 8 в тригонометрической форме (1.6),
для чего найдем модуль и главное значение аргумента z 8 8 ,
0 arg z arg 8 . Имеем z 8 8 cos i sin .
Применяя формулу (1.10), найдем 3 значения корня,
2k
2k
содержащихся в формуле Wk 3 8 cos
sin
, где
3
3
k 0,1,2 . Воспользовавшись показательной и тригонометрической
формами числа (1.6), (1.12), получаем
i
при k 0 w0 2e 3 2 cos i sin 1 i 3 ,
3
3
при k 1 w1 2e i 2 cos i sin 2 ,
5
3
5
5
2 cos
i sin 1 i 3 .
3
3
Точки w0 , w1 , w2 образуют вершины правильного треугольника,
вписанного в окружность радиуса 2 с центром в начале координат
(рис. 1.3).
при k 2 w2 2e
i

16.

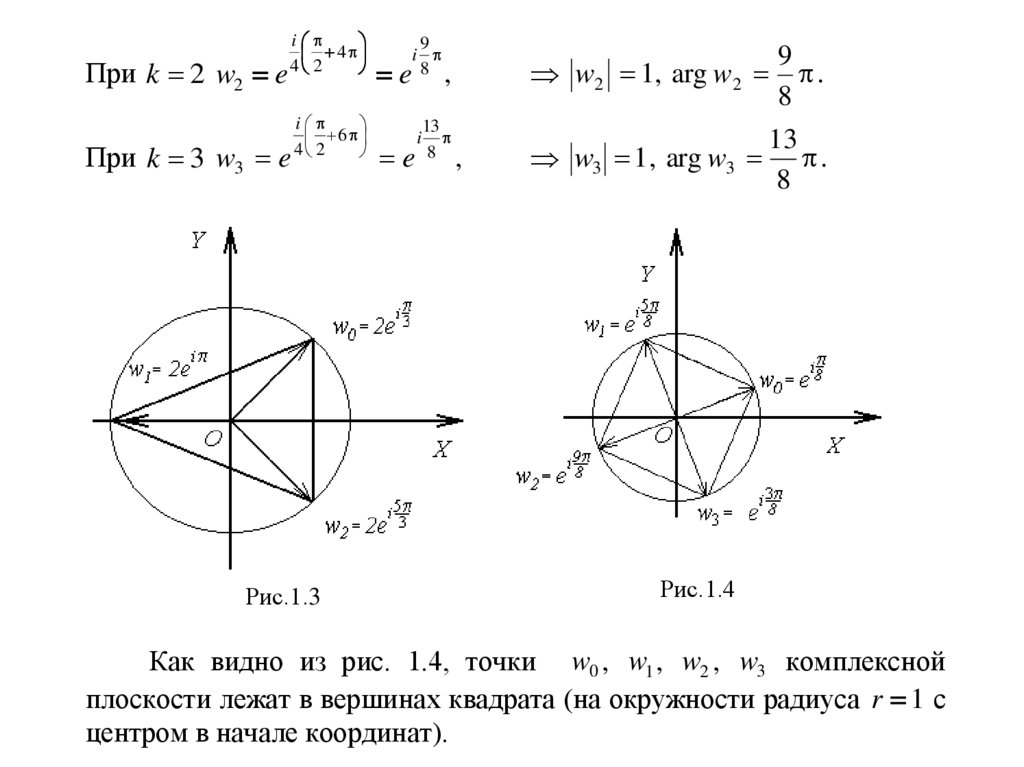
1. Решить уравнение w 4 i 0 .
Решение. Нахождение всех корней уравнения сводится к задаче:
найти все значения корня 4 i . Для чего запишем число i в
показательной
форме
i e
i
2
и применим
2 k
i 0
wk 4 1e 4 , где k 0,1,2,3, 0 .
2
i
8
формулу
При k 0 w0 e , откуда следует, что w0 1, arg w0
При k 1 w1 e
5
arg w1 .
8
i
2
4 2
e
5
i
8
.
8
, откуда следует, что w1 1 ,
(1.16)

17.

При k 2 w2 e
i
4
4 2
При k 3 w3 e
i
6
4 2
Рис.1.3
e
9
i
8 ,
e
i
13
8
w2 1, arg w2
,
w3 1 , arg w3
9
.
8
13
.
8
Рис.1.4
Как видно из рис. 1.4, точки w0 , w1 , w2 , w3 комплексной
плоскости лежат в вершинах квадрата (на окружности радиуса r 1 с
центром в начале координат).

18.

Кривые на комплексной плоскости
На множестве действительных чисел можно обычным образом
определить функцию, которая принимает на этом множестве
t T , T R
комплексные
значения:
любому
соответствует
z t Q, Q C , z t – комплекснозначная функция действительной
переменной t .

19.

Задание комплексной функции z t действительной переменной t на
некотором множестве T T R равносильно заданию на этом множестве
двух действительных функций x t Re z t и y t Im z t : z t x t iy t .
Для функции z t , так же как для действительной функции действительной
переменной вводится понятие предела в точке, понятие непрерывности,
производной, интеграла:
1. Для непрерывности функции z t в точке t0 T , необходимо и
достаточно, чтобы в этой точке были непрерывны функции
x t Re z t , y t Im z t .
2. lim z t lim x t i lim y t .
t t 0
t t 0
t t 0
3. z t x t iy t , dz dx idy .
b
b
b
a
a
a
4. z t dt x t dt i y t dt .
(2.1)

20.

Непрерывная на отрезке T функция z (t ) задает в C кривую L .
При этом кривая L называется гладкой, если z t непрерывна и
z (t ) 0 на T .
Кривая называется кусочно-гладкой, если ее можно разбить на
конечное число гладких кривых.
Уравнение гладкой кривой может быть записано в виде
F x, y 0 ; в частности y f x – явное задание линии. Из z x iy и
z z
z z
и y
. Поэтому равенство
z x iy получаем x
2
2i
z z z z
0
F
,
(2.3)
2i
2
есть уравнение кривой на плоскости , записанное в комплексной
форме.