Похожие презентации:
Электрические и магнитные дипольные моменты и энергия взаимодействия микрочастиц с внешним полем
1. 1.4. Взаимодействие электромагнитного излучения с веществом
1.4.1. Электрические и магнитные дипольныемоменты и энергия взаимодействия микрочастиц
с внешним полем
2.
Рассмотрим взаимодействие электромагнитного поля с элементами вещества –атомами, молекулами или ионами. Такое взаимодействие возможно благодаря наличию
у них дипольных, квадрупольных и мультипольных электрических и магнитных
моментов. Для нейтрального атома, содержащего ядро и отрицательно заряженный
электрон, дипольный момент равен:
где
pr = err ,
rr
(1.4.1)
- радиус-вектор, соединяющий электрон с ядром,
e - элементарный
электрический заряд. Для более сложного атома полный дипольный момент может быть
получен как векторная сумма частных моментов.
Если рассматриваемый атом находится во внешнем поле с электрической
r
напряженностью E
r .r
V = p E
, то энергия взаимодействия диполя с полем равна:
(1.4.2)
3.
r rr
При квантовомеханическом рассмотрении величины p , r и E нужно заменить
операторами. Мы будем пользоваться полуклассическим приближением, когда поле
рассматривается классически (не квантуется):
)
r) r
(1.4.3)
,
=
V
p
E
)r
)r
=
где p er - оператор электродипольного момента. В энергетическом представлении
)r
p изображается матрицей с элементами:
r
r
* )
(1.4.4)
=
y
,
p mn
m e r y n dV
где
V
r
y m (r , t )
- собственные функции оператора энергии.
Обычно функции y m , входящие в (1.4.4), обладают определенной четностью, то
есть каждая из этих функций либо четная, либо нечетная функция координат. Тогда
*
при m=n произведение y my m = y m
2
является четной функцией, а
нечетная функция. Поэтому диагональные матричные элементы оператора
электродипольного момента равны нулю:
* r
ym
ry m -
4.
rpmm = 0 .
(1.4.5)
r
Кроме того, те из p mn , которые соответствуют состояниям с одинаковой четностью,
также равны нулю. Это означает, что
электродипольные переходы между
состояниями с одинаковой четностью запрещены.
Если атом (частица) обладает магнитным моментом, то он также будет
взаимодействовать с электромагнитным полем:
)r r
)
V = H ,
r
H
за счет составляющей .
(1.4.6)
r
Самым сильным является электродипольное взаимодействие. Если же pmn = 0,
r
r
то следует учесть магнитодипольное взаимодействие. При pmn = 0 и mn = 0
взаимодействие частицы с полем является слабым и осуществляется за счет
.
квадрупольных и мультипольных электрических моментов.
5. 1.4.2. Двухуровневая система микрочастиц во внешнем поле. Основные уравнения. Вероятности индуцированных переходов
Рассмотрим ансамбль микрочастиц, находящихся во внешнемэлектромагнитном поле. Полагаем, что у данных частиц имеется
пара энергетических уровней 1 и 2, расстояние между которыми
E2 E1 = 21 соответствует частоте 21 , близкой к частоте
приложенного поля
. Тогда наличием всех прочих уровней
можно
и
рассматривать
пренебречь
двухуровневую.
данную
систему
как
6.
Нас интересует мощность P, поглощаемая веществом,которая, как было показано ранее, равна:
P = W ( N1 N 2 )
(1.4.7)
Здесь нам неизвестны как вероятность индуцированных
переходов, так и населенности уровней N1 и N2. Последние можно
выразить через диагональные элементы матрицы плотности:
N k = kk N , где N – полное число частиц.
Таким образом, расчет поглощаемой мощности связан с
решением уравнений для матрицы плотности.
7.
В случае двухуровневой системы общие уравнения длясущественно упрощаются. Найдем вначале матричные элементы
оператора энергии взаимодействия микрочастицы с полем:
V11 = p11 E = 0,V22 = p22 E = 0,
V12 = p12 E ,V21 = p21 E.
(1.4.8)
С учетом этого запишем уравнения для матричных элементов
12 :
и
d 11
i
= 21 22 12 11 12V21 V12 21 ,
dt
d 12 12
i
i 21 = 11V12 V12 22 ,
dt
где учтено: 12 = 21 = .
(1.4.9)
(1.4.10)
11
8.
Уравнения (1.4.9) и (1.4.10) содержат 4 неизвестных, 11 , 22 ,12 и 21 . Поэтому к ним нужно добавить еще 2 уравнения. В
качестве таковых можно использовать общее соотношение,
Sp = 1 , которое в данном случае имеет вид:
11 22 = 1,
и учесть условие самосопряженности матрицы
12* = 21 .
(1.4.11)
:
(1.4.12)
Система уравнений (1.4.9)-(1.4.12) позволяет определить все
элементы матрицы плотности.
9.
Для ее решения выпишем в явном виде значения Vik. Для поляE (t ) = Em cos( t ) имеем:
p12 Em
V12 =
exp(i t ) exp( i t ) .
2
(1.4.13)
Входящая в уравнение (1.4.10) вынуждающая сила в этом случае
содержит две составляющие, пропорциональные
exp( i t )
.
Поскольку
собственные
exp(i t )
колебания
и
системы,
определяемые левой частью (однородным уравнением), происходят
по закону exp( t ) exp(i 21t ) , то основной вклад в решение даст
«резонансное» слагаемое в (1.4.13), пропорциональное exp(i t ) :
V12
p12 Em
exp(i t ) .
2
(1.4.14)
10.
Из условия самосопряженности находим:p12* Em
V21 = V =
exp( i t )
2
*
12
Отыскивая решение в виде
12 = 12m exp(i t )
(1.4.15)
, где
12m
-
медленно меняющаяся функция времени, так что ее производной
можно пренебречь, из (1.4.10) находим:
12m =
(i )( p12 Em 2)
( 11 22 ) .
1 i ( 21 )
(1.4.16)
11.
Учитывая соотношение ( i )V12 21 = (i )V21 12 , найдем последний*
член в правой части уравнения (1.4.9):
i
2
1 p12 Em
1
1
( 12V21 V12 21 ) =
( 11 22 )
4
1 i ( 21 ) 1 i ( 21 )
=
2
(1/ 2 ) ( p12 Em )
1/ ( 21 )
2
2
( 11 22 ).
Подставляя это выражение в (1.4.9) и вводя обозначения
/(2 )
p12 Em
W=
, =
,
2
2
1/ ( 21 )
2
(1.4.17)
окончательно получаем:
d 11
= ( 21 W ) 22 ( 12 W ) 11 .
dt
(1.4.18)
12.
Рассмотрим физический смысл членов, входящих в данноеуравнение.
В левой части определяется относительная скорость изменения
числа частиц на нижнем уровне с энергией E1. Первый член в правой
части характеризует приток частиц на данный уровень. Тепловые
(безызлучательные) переходы имеют вероятность 21 , а величина W
определяет, очевидно, вероятность индуцированного перехода одной
частицы в единицу времени.
Второе слагаемое в правой части (1.4.18), характеризующее
отток
частиц
с
уровня
1,
показывает,
что
вероятности
индуцированного перехода сверху вниз и снизу вверх одинаковы, и в
случае двухуровневой системы частиц определяются формулами
(1.4.17).
13.
Определим мощность, поглощаемую двухуровневой системой,для стационарного случая, когда d 11 dt = d 22 dt = 0 . Из (1.4.18)
получаем:
( 21 W ) 22 ( 12 W ) 11 = 0 .
(1.4.19)
Используя соотношение (1.4.11), находим:
11 =
21 W
12 W
, 22 =
,
21 12 2W
21 12 2W
21 12
11 22 =
.
21 12 2W
(1.4.20)
(1.4.21)
14.
Переписывая уравнение детального равновесия в виде11e
22e
=
= T1 ,
21 12
(1.4.22)
где величина T1 имеет размерность времени и характеризует
скорость релаксации за счет взаимодействия с термостатом,
вместо (1.4.21) можно получить:
1
11 22 =
( 11e 22e ) .
1 2WT1
(1.4.23)
15.
Такимобразом, поглощаемая двухуровневой
мощность может быть найдена в виде:
e
P = 21W ( N1 N 2 ) = 21WN ( 11e 22
)=
W
e
= 21 N
( 11e 22
).
1 2WT1
(1.4.24)
системой
16. 1.4.3. Анализ поглощения электромагнитного поля двухуровневой системой. Эффект насыщения
Применим общее выражение (1.4.24) для анализа двух предельныхслучаев.
1.
Слабое поле, вероятность индуцированного перехода W 1/ T1 . Тогда
слагаемым 2WT1 в знаменателе можно пренебречь. Подставляя в (1.4.24) для
этого случая W из формулы (1.4.17), получаем:
/(2 )
P = 21 N ( 11e 22e )
.
1/ 2 ( 21 ) 2
2
(1.4.25)
Отсюда видно, что мощность, поглощаемая от поля веществом,
пропорциональна квадрату напряженности внешнего поля, а значит,
пропорциональна его мощности.
Такая связь характерна для линейной
параметры среды не зависят от величины поля.
электродинамики,
когда
17.
Частотная зависимость поглощаемой мощности описываетсяфункцией
g ( ) =
1/( )
,
2
2
1/ ( 21 )
(1.4.26)
называемой кривой Лоренца, и совпадающей по виду с резонансной
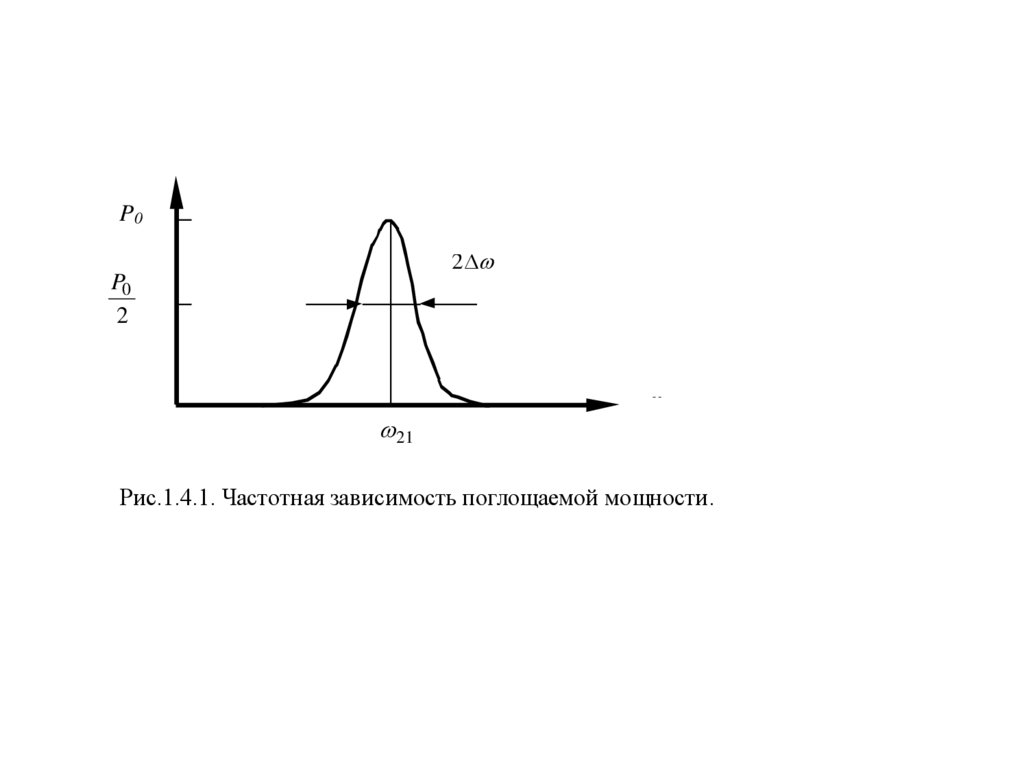
кривой простого колебательного контура (рис. 1.4.1).
Максимум поглощения достигается при частоте внешнего поля
= 21 . Полуширина кривой по уровню 0.5 равна = 1/ .
Отсюда следует, что время релаксации
можно определить
экспериментально, если снять частотную зависимость поглощаемой
мощности.
18.
P02
P0
2
21
Рис.1.4.1. Частотная зависимость поглощаемой мощности.
19.
2. Сильное поле, вероятность индуцированного перехода Wсравнима с вероятностью переходов под действием термостата 1/T1.
В этом случае из (1.4.24) и (1.4.17) получаем:
P = 21 N ( 11e 22e )
1 2
2
1
T1 2
2
(
)
21
2
.
(1.4.27)
Отсюда видно, что связь между мощностями внешнего поля и
поглощаемой веществом нелинейна. Когда внешнее поле очень
велико ( ), мощность поглощения не зависит от внешнего
2
поля и равна:
Psat = 21 N ( 11e 22e )
1
.
2T1
(1.4.28)
20.
Величина предельной мощности поглощения определяетсяскоростью, с которой энергия передается термостату, 1/T1.
График зависимости поглощаемой мощности от мощности
2
падающего излучения Pinp ~ Em ~ схематично изображен на
рис. 1.4.2.
2
21.
PPsat
Pinp ~
I
II
2
III
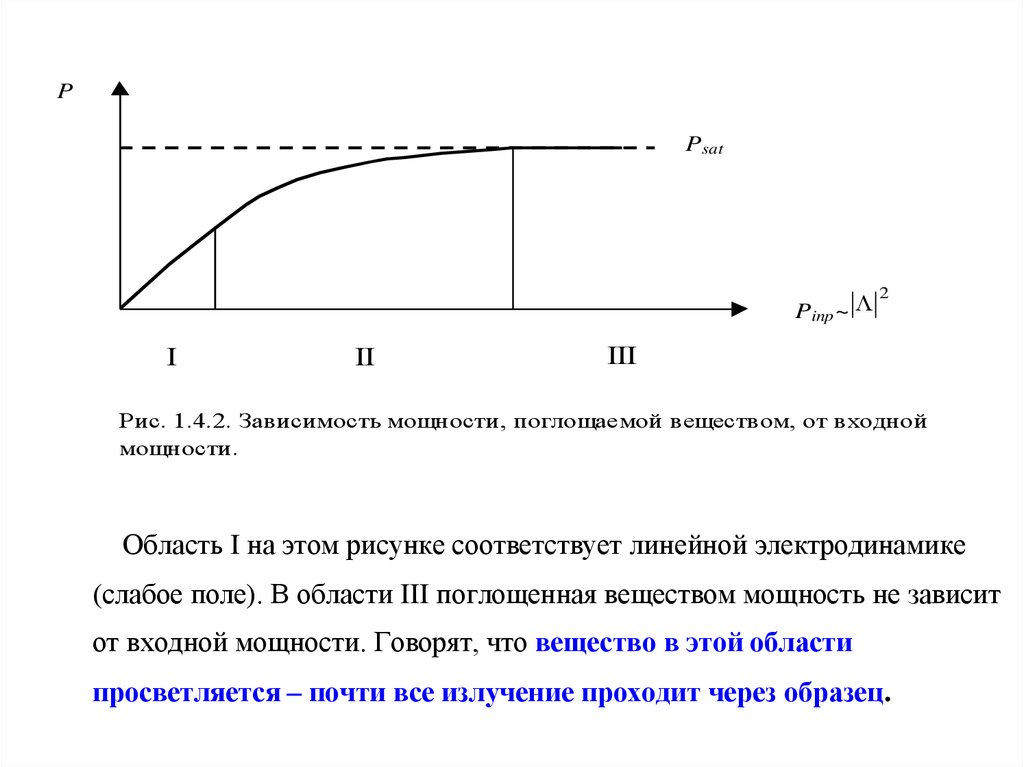
Рис. 1.4.2. Зависимость мощности, поглощаемой веществом, от в ходной
мощности.
Область I на этом рисунке соответствует линейной электродинамике
(слабое поле). В области III поглощенная веществом мощность не зависит
от входной мощности. Говорят, что вещество в этой области
просветляется – почти все излучение проходит через образец.
22.
Нелинейностьзависимости
поглощаемой
мощности
от
падающей мощности называют эффектом насыщения.
Физической причиной насыщения является выравнивание
населенностей уровней, 11
индуцированных
переходов
и 22 , при увеличении вероятности
W.
Действительно,
из
(1.4.23)
получаем:
11 22 ( 11e 22e )
1
,
2WT1
(1.4.29)
и видим, что разность населенностей уровней ( 11 22 ) 0
WT1 .
при
23. 1.4.4. Спонтанные переходы
В предыдущих разделах 1.4.2 и 1.4.3 учитывались толькоиндуцированные и тепловые (безизлучательные) переходы. Кроме
них, существуют спонтанные (самопроизвольные) переходы с
верхнего на нижний уровень. При Em En имеем:
Amn 0, Anm = 0 ,
где
Amn
(1.4.30)
- вероятность спонтанного перехода одной частицы в
единицу времени с m-го на n-й уровень. Следует напомнить, что при
спонтанном переходе излучается поле с произвольной фазой,
поляризацией и направлением распространения во всем телесном
угле.
24.
Частотная зависимость мощности спонтанного излученияопределяется функцией g ( ) = (1/ ) / 1/ 2 ( 21 ) 2 , где
= 1/ A21 .
Вероятность спонтанного перехода была найдена А. Эйнштейном
из анализа формулы Планка для равновесного излучения абсолютно
черного тела в виде (в системе единиц СГСЕ):
8 321
A21 = 3 B ,
c
где
B = [(4 2 ) /(3 2 )] p12
частота перехода в Гц.
(1.4.31)
2
- коэффициент Эйнштейна и 21
-
25.
Отметим, что A21 ~ 321 . Поэтому очень велико значениеспонтанных переходов для оптического диапазона.
Для безизлучательных переходов вероятность
при
mn ~ kT
mn
велика
. Это означает, что их роль является
определяющей в СВЧ-диапазоне, где mn Amn , и мала в
оптическом диапазоне, где mn Amn .
26. 1.4.5. Балансные уравнения
Однаиз
задач
квантовой
электроники
–
нахождение
распределения числа частиц по энергетическим уровням. Её
строгое решение может быть проведено на основе общих
уравнений для матрицы плотности и электромагнитного поля,
когда
учитывается
динамика
как
диагональных,
так
и
недиагональных элементов.
Существует приближенный подход, когда используются
балансные (кинетические) уравнения для числа частиц на
энергетических уровнях.
27.
Вспомним в качестве примера уравнения для двухуровневойсхемы:
d 11
= 21 22 12 11 W 22 W 11 .
dt
Здесь не учтены спонтанные переходы и наличие других
уровней. В общем случае запишем следующее
балансное
(кинетическое) уравнение:
dN m
= ( nm N n mn N m ) Wnm ( N n N m ) ( Anm N n Amn N m ) .
dt
n m
n m
n m
Данная методика, основанная на уравнениях баланса, будет
использоваться нами довольно часто при анализе энергетических
характеристик лазеров.

























 Физика
Физика