Похожие презентации:
Начертательная геометрия. Точка, линии
1.
НАЧЕРТАТЕЛЬНАЯГЕОМЕТРИЯ
Курс лекций –к.т.н. Н.И.Красовская
2.
Основоположником начертательнойгеометрии считается французский
ученый ГАСПАР МОНЖ
(1799 г. –первый учебник )
3.
Россиявпервые появились понятия:
«Чертеж» - 1578 г.,
«Чертещик» - 1638 г.
«Бок,полуширота,корпус» - эпоха Петра I
(фронтальная,
горизонтальная
и профильная
проекции)
4.
Впервые курс начертательной геометриичитается в учебных заведениях - 1810 г.;
Первый учебник «Основания начертательной
геометрии» -1821 г.- (Я.А. Севастьянов);
Большой вклад в развитие начертательной
геометрии внесли русские ученые:
В.И. Курдюмов, Е.С. Федоров, Н.А. Рынин,
Н.Ф. Четверухин, А.В. Бубенников,
И.И. Котов, С.А. Фролов и др.
5.
«Если чертеж является языком техника,одинаково понятным всем народам, то
начертательная геометрия служит
грамматикой этого мирового языка,
так как она учит нас правильно читать чужие и
излагать наши собственные мысли,
пользуясь в качестве слов одними
только линиями и точками
как элементами всякого изображения»
В.И.Курдюмов
(Из книги «Курс начертательной геометрии»)
6.
Цель изучения дисциплиныПриобретение необходимых знаний,
умений и навыков отображать
всевозможные
сочетания геометрических форм
трёхмерного пространства на
двухмерном(плоском) носителе: листе
бумаги, экране дисплея и т.д.
7.
Задачи- знать основные понятия, определения и свойства
ортогонального проецирования;
- иметь представление об образовании различных
геометрических объектов с позиции кинематики;
- уметь задавать на двухмерном носителе любые
геометрические объекты пространства;
- уметь определять расположение объектов в
пространстве относительно плоскостей проекций
и относительно друг друга;
- приобрести умения и навыки графического
решения типовых задач
8.
Компоненты аппаратаграфического общения
Объект отображения
Способ образования объекта отображения
Элементы, формообразующие объект
Носитель графической информации
Способ отображения объекта
Средства отображения объекта
Процесс отображения объекта
9.
Лекция 1МЕТОД
ПРОЕКЦИЙ
Н.И.Красовская
10.
Основные понятияН.И.Красовская
11.
Геометрическое пространствомножество точек, каждая из которых неимеет величины, но имеет определённое
положение относительно выбранного
объекта(образа) в пространстве
Н.И.Красовская
12.
Геометрический объект (образ)это множество точек, выделенных изпространства и подчинённых
определённым условиям
Н.И.Красовская
13.
Отображение –это правило, которое устанавливает
принцип однозначного соответствия
точек трёхмерного пространства и
вполне определённых точек двухмерного
пространства (плоскости)
Н.И.Красовская
14.
Проецирование –процесс отображения геометрических
объектов трёхмерного пространства на
двухмерном носителе - плоскости с
помощью проецирующих лучей
Н.И.Красовская
15.
Проекция –изображение геометрического объекта,
полученное в результате
проецирования
Н.И.Красовская
16.
Н.И.Красовская17.
ТОЧКАН.И.Красовская
18.
Точка –0–мерный объект
Отобразить точку, значит,
построить ее проекции
Н.И.Красовская
19.
Аппарат проецированияН.И.Красовская
20.
Sa
П1
А
А1
Н.И.Красовская
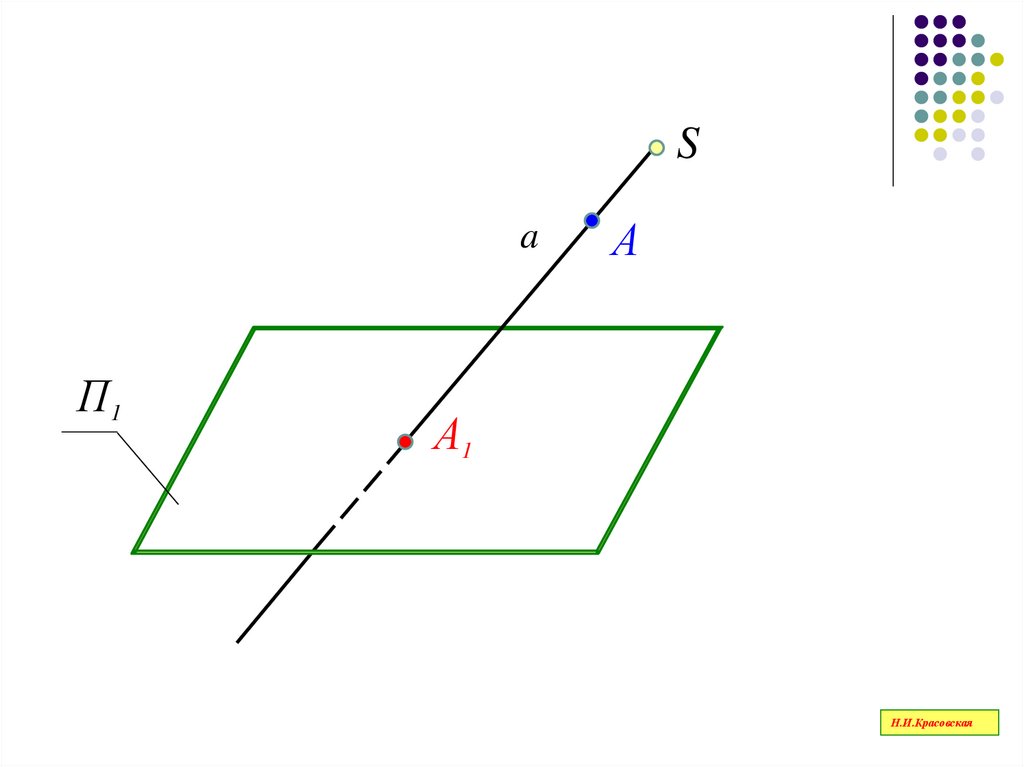
21.
Аппарат проецирования- объект проецирования – (А);
- плоскость проекций – (П1);
- центр проецирования – ( S );
- проецирующий луч –( a );
-проекция объекта – (А1)
Н.И.Красовская
22.
Точки обозначаются прописными буквамилатинского алфавита A, B,C, D и т. д.
Линии - строчными буквами того же
алфавита a,b,c,d и т.д.
Плоскости проекций - греческой буквой
П (П1 П2 П3 и т.д.)
Н.И.Красовская
23.
Видыпроецирования
Н.И.Красовская
24.
Sb
a
В
А
П1
Н.И.Красовская
В1
А1
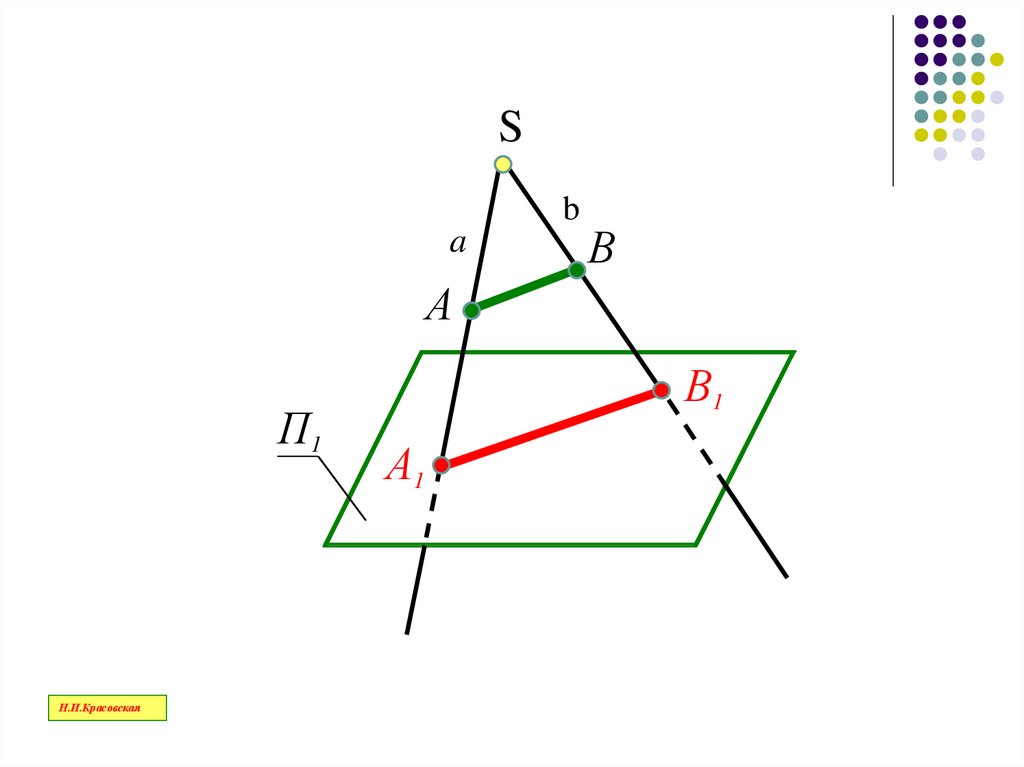
25.
Вид проецирования, при которомпроецирующие лучи исходят из одной
точки - центра проецирования,
называется
центральным
Н.И.Красовская
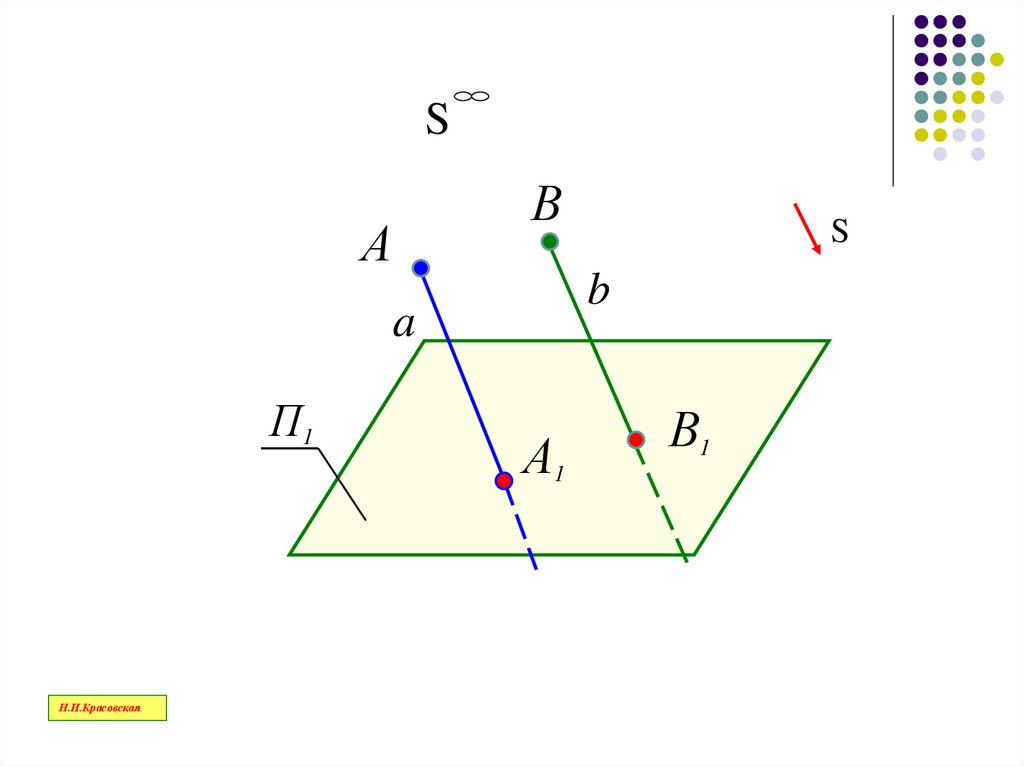
26.
Вид проецирования, при котором центрпроецирования удален в бесконечность, а
проецирующие лучи параллельны друг
другу, называется
параллельным
Н.И.Красовская
27.
SВ
А
b
a
П1
Н.И.Красовская
S
А1
В1
28.
Вид проецирования, при которомпроецирующие лучи проходят
не перпендикулярно
к плоскости проекций, называется
косоугольным
Н.И.Красовская
29.
Вид проецирования, при которомпроецирующие лучи проходят
перпендикулярно
плоскости проекций, называется
прямоугольным или ортогональным
Н.И.Красовская
30.
SА
a
П1
А1
Н.И.Красовская
В
b
В1
S
31.
Основным видом проецированияв начертательной геометрии
является
ортогональный
Н.И.Красовская
32.
Основные свойствапараллельного
проецирования
Н.И.Красовская
33.
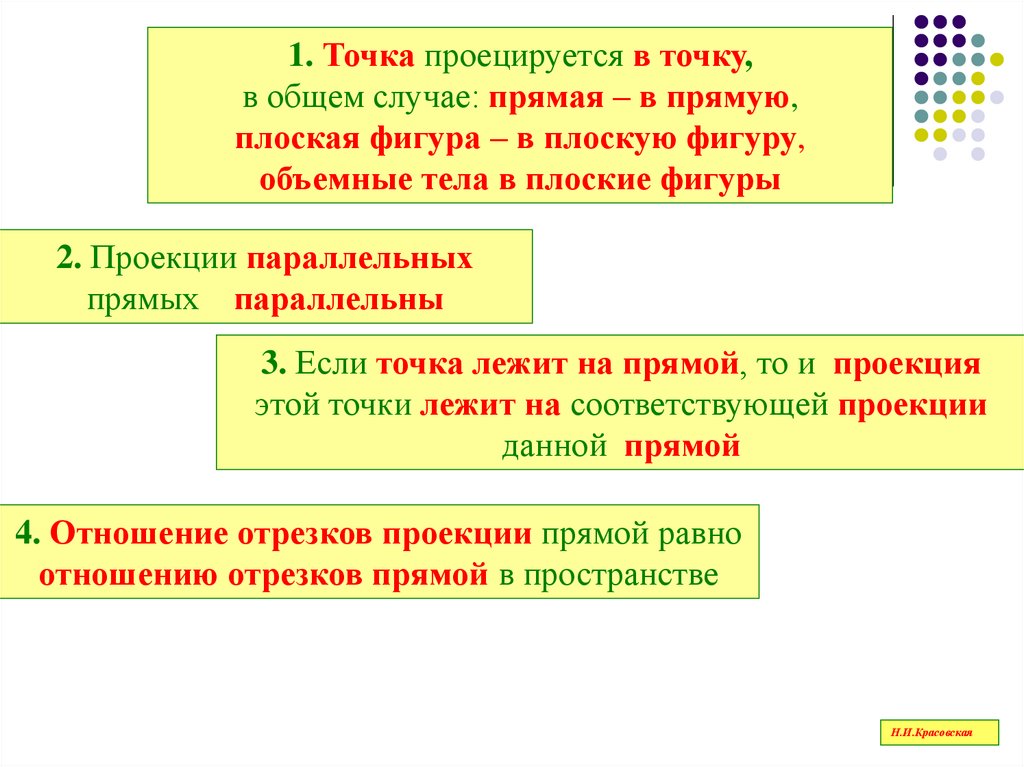
1. Точка проецируется в точку,в общем случае: прямая – в прямую,
плоская фигура – в плоскую фигуру,
объемные тела в плоские фигуры
2. Проекции параллельных
прямых параллельны
3. Если точка лежит на прямой, то и проекция
этой точки лежит на соответствующей проекции
данной прямой
4. Отношение отрезков проекции прямой равно
отношению отрезков прямой в пространстве
Н.И.Красовская
34.
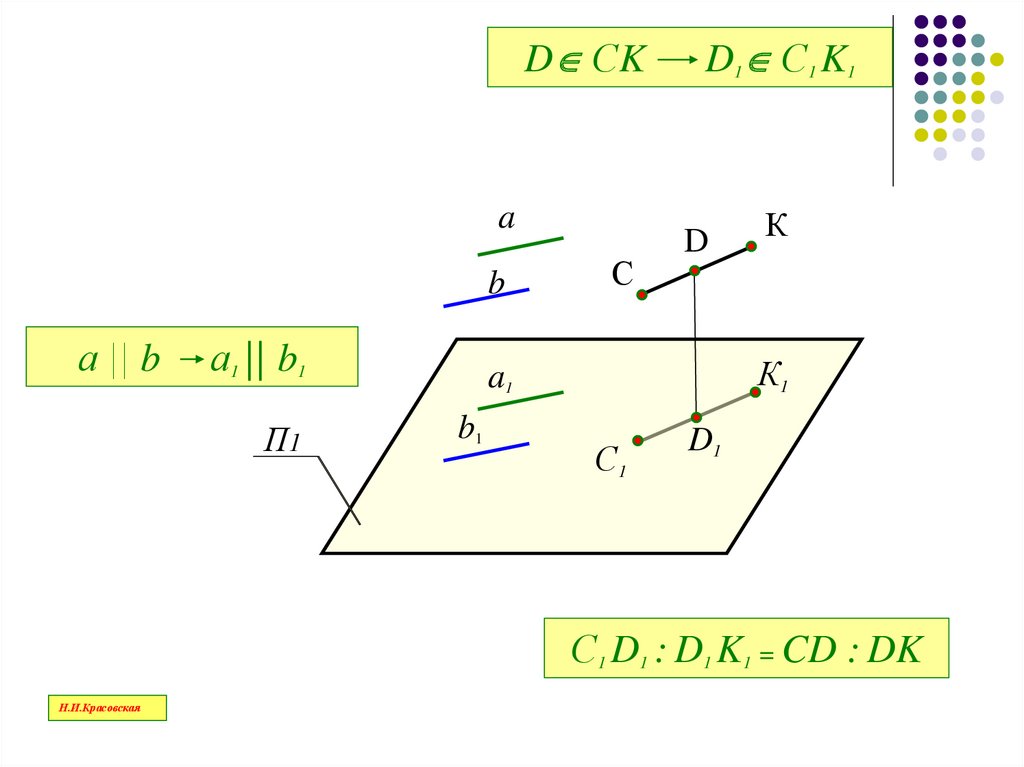
D СKa
b
а || b
а1 || b1
П1
С
D1 С1 K1
D
К1
a1
b1
К
С1
D1
С1 D1 : D1 K1 = CD : DK
Н.И.Красовская
35.
Обратимость чертежа.Координаты точки.
Комплексный чертеж точки
Н.И.Красовская
36.
Обратимый чертеж –это чертеж, позволяющий однозначно
определять форму, размеры и положение
предмета в пространстве
Н.И.Красовская
37.
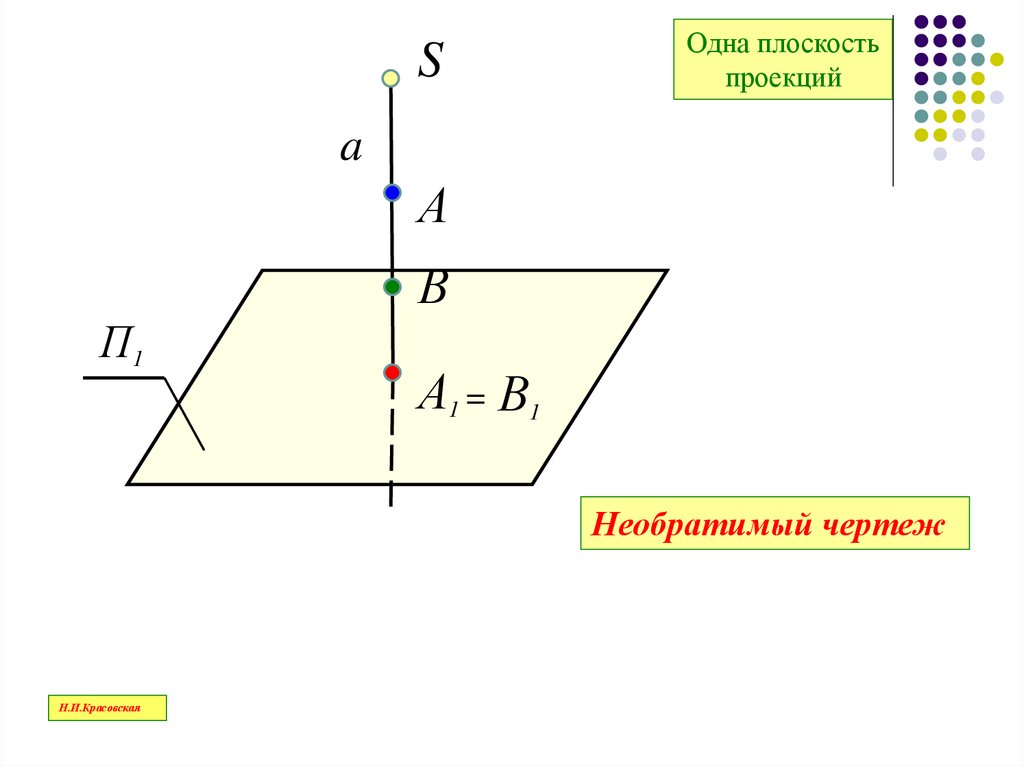
SОдна плоскость
проекций
a
А
В
П1
А1 = В1
Необратимый чертеж
Н.И.Красовская
38.
Три плоскости проекцийП2
II
z
VI
I
V
x
П1
III
у
IV
VIII
П3
Н.И.Красовская
VII
39.
Плоскости проекций бесконечны, непрозрачныи взаимно перпендикулярны
П1- горизонтальная плоскость проекций,
П2- фронтальная плоскость проекций,
П3- профильная плоскость проекций
Линии пересечения плоскостей проекций
называются осями проекций
Линия пересечения П1 и П2 – ось Х,
линия пересечения П2 и П3 – ось Z,
линия пересечения П1 и П3 –ось У
Точка пересечения осей проекций –
начало координат 0
Н.И.Красовская
40.
Координатой точкиназывается
расстояние от точки
до плоскости проекций
Н.И.Красовская
41.
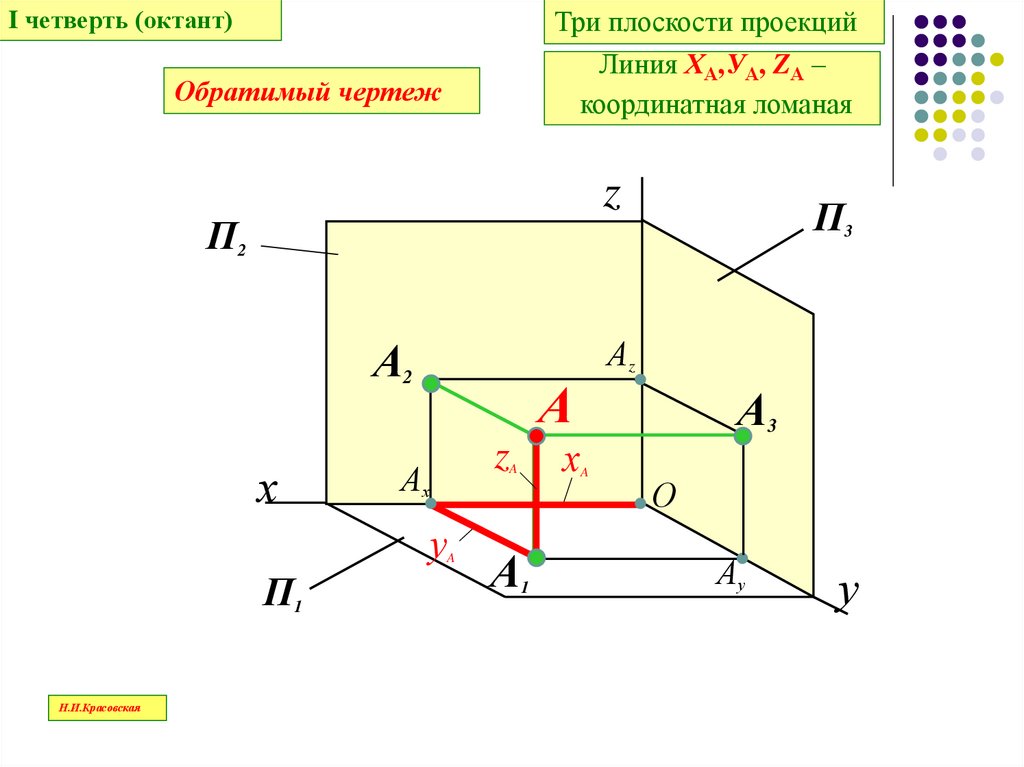
I четверть (октант)Три плоскости проекций
Линия ХА,УА, ZА –
координатная ломаная
Обратимый чертеж
z
П2
Аz
А2
х
А
z
Ах
у
A
П1
Н.И.Красовская
П3
А3
х
A
A
А
1
О
Ау
у
42.
Х - расстояние от точки до плоскостипроекций П3- широта точки
У - расстояние от точки до плоскости проекций
П2- глубина точки
Z- расстояние от точки до плоскости проекций
П1- высота точки
Н.И.Красовская
43.
Координаты измеряются в миллиметрах изаписываются в следующем порядке:
Х,У, Z,
например,
А(30,20,10)
Н.И.Красовская
44.
Для удобства плоскости проекцийразворачивают и совмещают
с фронтальной плоскостью проекций
Получается
комплексный чертеж - эпюр
(«очищенный»-франц.)
Н.И.Красовская
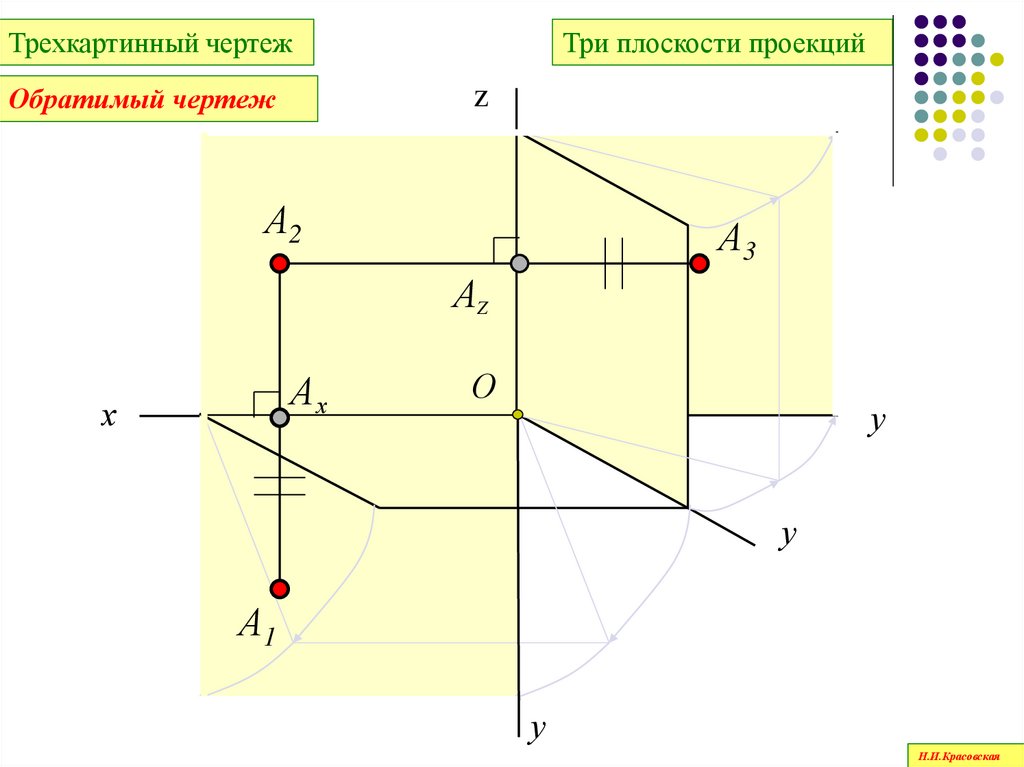
45.
Трехкартинный чертежТри плоскости проекций
z
Обратимый чертеж
А2
А3
АZ
Ах
х
О
у
у
А1
у
Н.И.Красовская
46.
Ось У раздваивается,но расстояния по обеим осям
всегда равны!!!
Н.И.Красовская
47.
Пространство являетсятрехмерным
Любая проекция определяется двумя
координатами, поэтому она является
двумерной
Н.И.Красовская
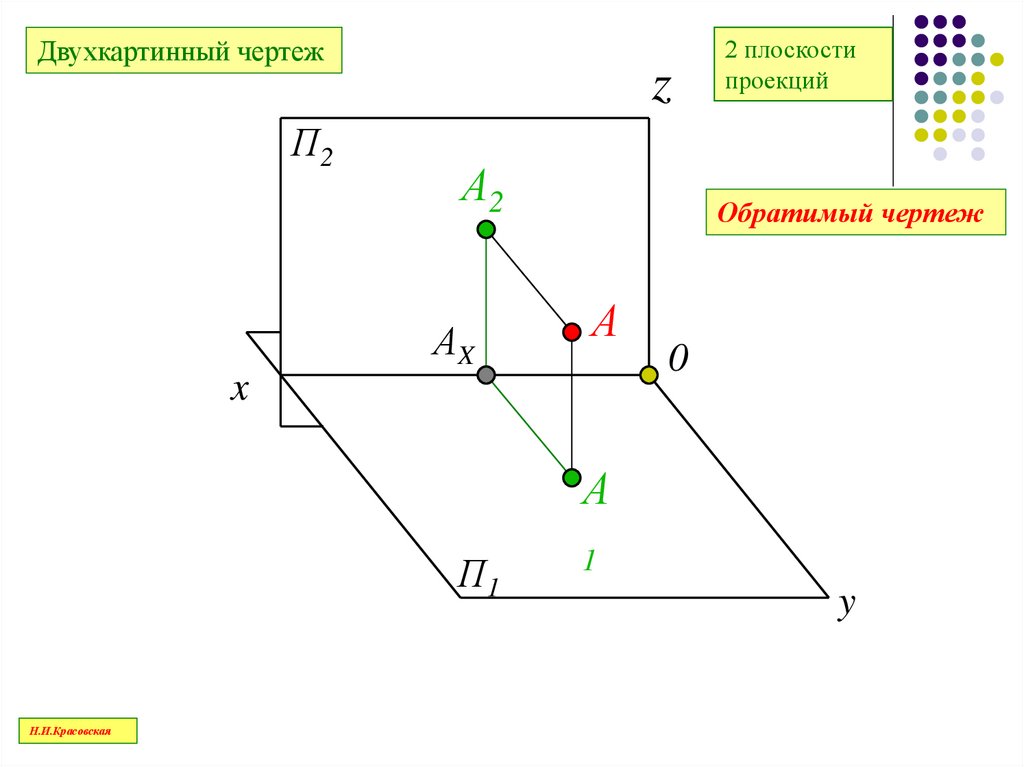
48.
Двухкартинный чертежП2
z
А2
АX
2 плоскости
проекций
Обратимый чертеж
А
x
0
А
П1
Н.И.Красовская
1
y
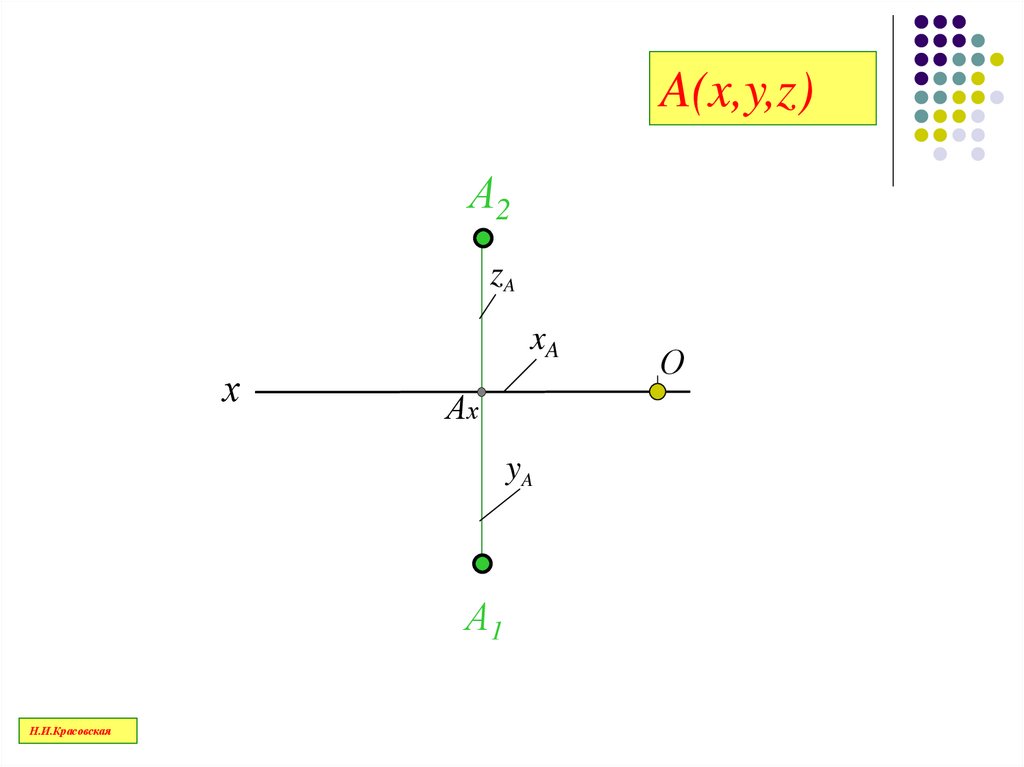
49.
A(x,y,z)А2
zA
xA
х
Ах
yA
А1
Н.И.Красовская
О
50.
Точки общегои частного положения
Н.И.Красовская
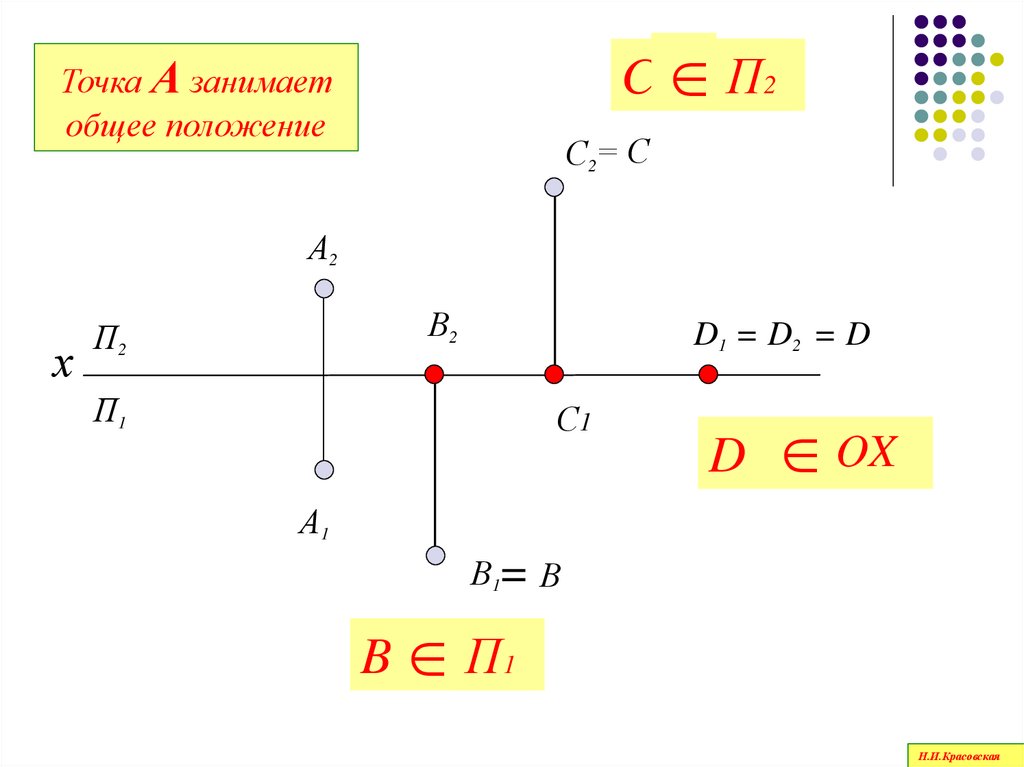
51.
C П2Точка А занимает
общее положение
С2= С
А2
х
В2
П2
D1 = D2 = D
П1
С1
D
OX
А1
В1= В
B П1
Н.И.Красовская
52.
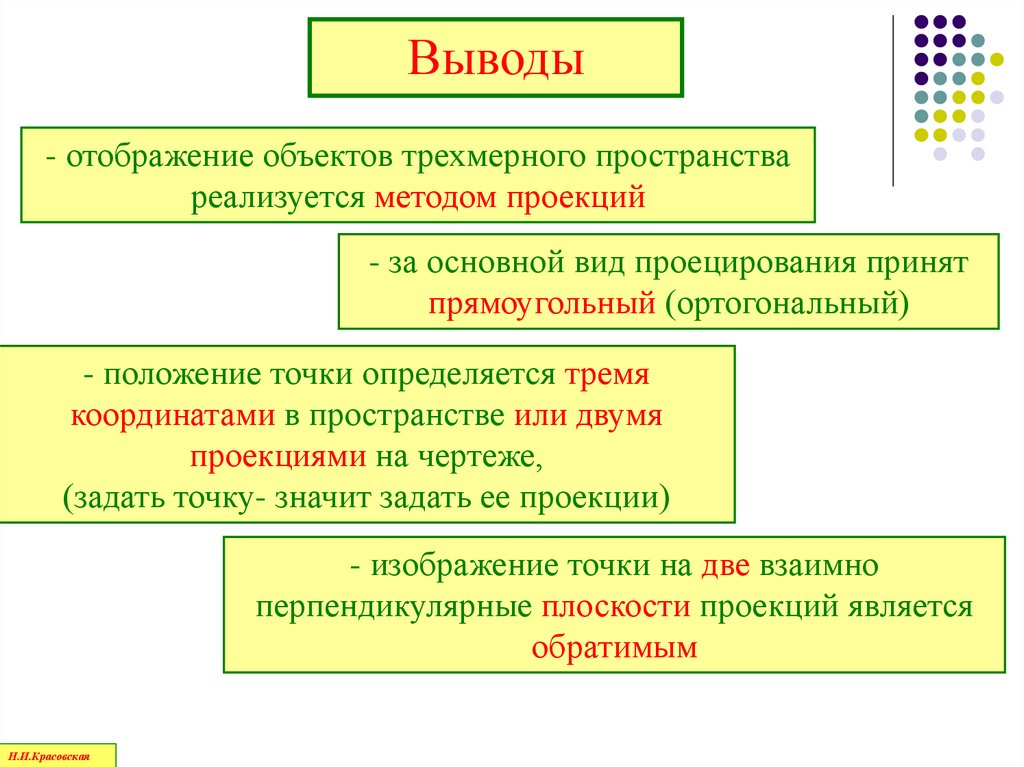
Выводы- отображение объектов трехмерного пространства
реализуется методом проекций
- за основной вид проецирования принят
прямоугольный (ортогональный)
- положение точки определяется тремя
координатами в пространстве или двумя
проекциями на чертеже,
(задать точку- значит задать ее проекции)
- изображение точки на две взаимно
перпендикулярные плоскости проекций является
обратимым
Н.И.Красовская
53.
Лекция 2ЛИНИИ
Красовская Н.И.
54.
Линия –это множество положений
непрерывно движущейся в
пространстве точки
Линия – это одномерный
геометрический объект
Красовская Н.И.
55.
Прямая линияКрасовская Н.И.
56.
Простейшей линией являетсяпрямая линия
Прямая получается при непрерывном
движении точки без изменения ее направления
Прямая линия является одномерным объектом
Красовская Н.И.
57.
Задание прямой линии начертеже.
Определитель прямой
Красовская Н.И.
58.
Совокупность элементов, задающихпрямую в пространстве,
называется ее
определителем
Красовская Н.И.
59.
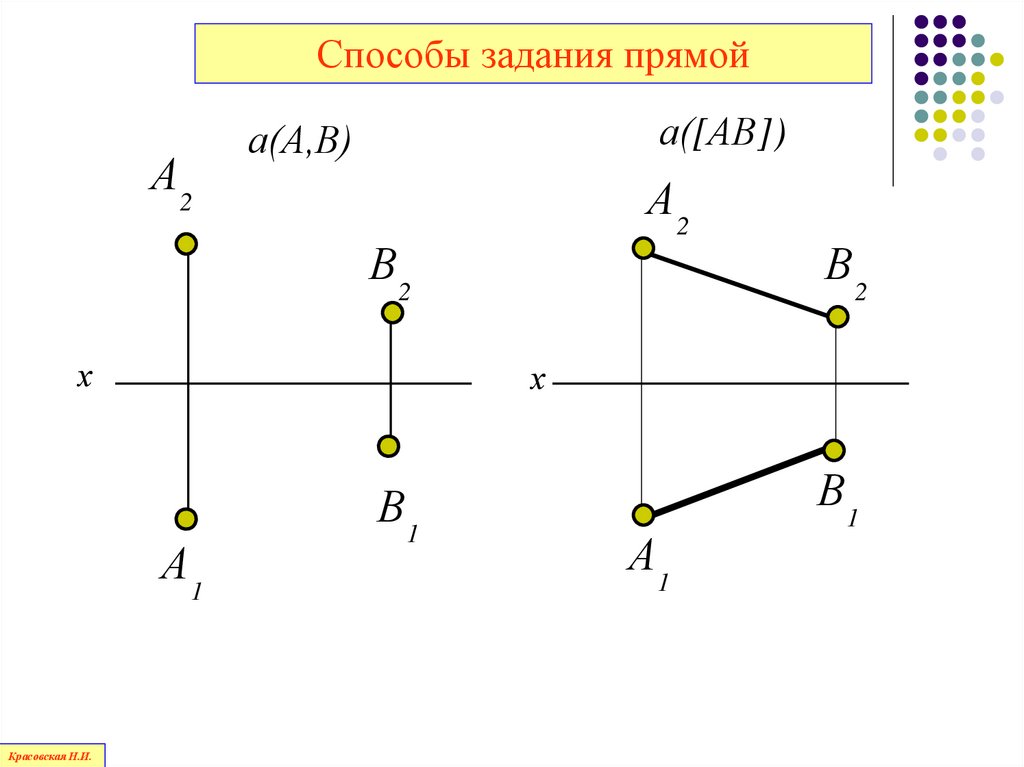
Способы задания прямойА2
а([АВ])
а(А,В)
А2
В2
х
х
А1
Красовская Н.И.
В2
В1
А1
В1
60.
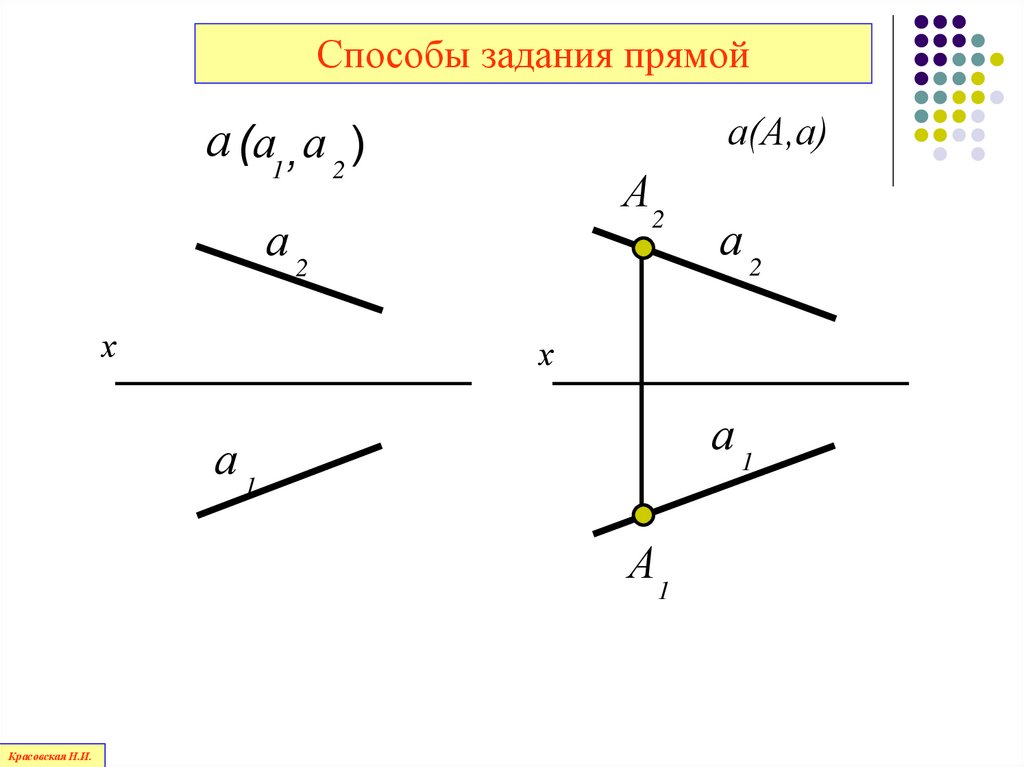
Способы задания прямойа(А,а)
а (а1 , а 2 )
А2
а2
х
х
а1
а1
А1
Красовская Н.И.
а2
61.
Положение прямой линии впространстве
Красовская Н.И.
62.
Прямая в пространстве может занимать дваположения:
общее и частное
Красовская Н.И.
63.
Прямыеобщего положения
Красовская Н.И.
64.
Прямые, не параллельные и неперпендикулярные ни одной из плоскостей
проекций, называются
прямыми общего положения
Красовская Н.И.
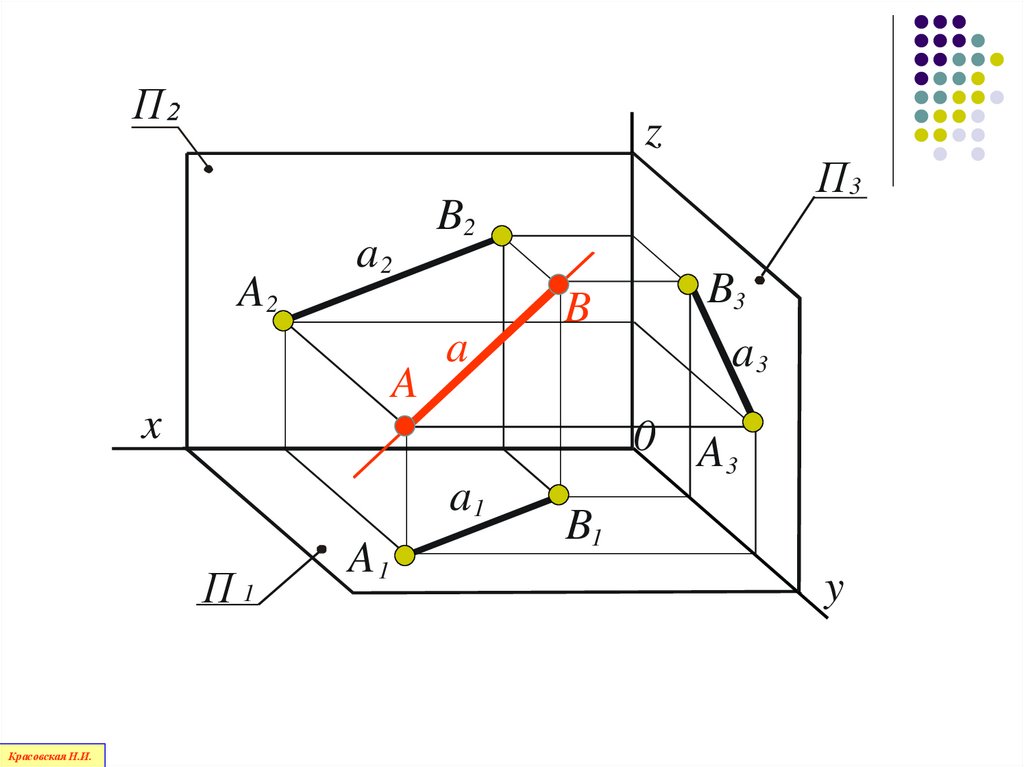
65.
Пz
A2
a2
A
B2
a
B
x
B3
a3
0 A
3
a1
П1
Красовская Н.И.
П3
A1
B1
y
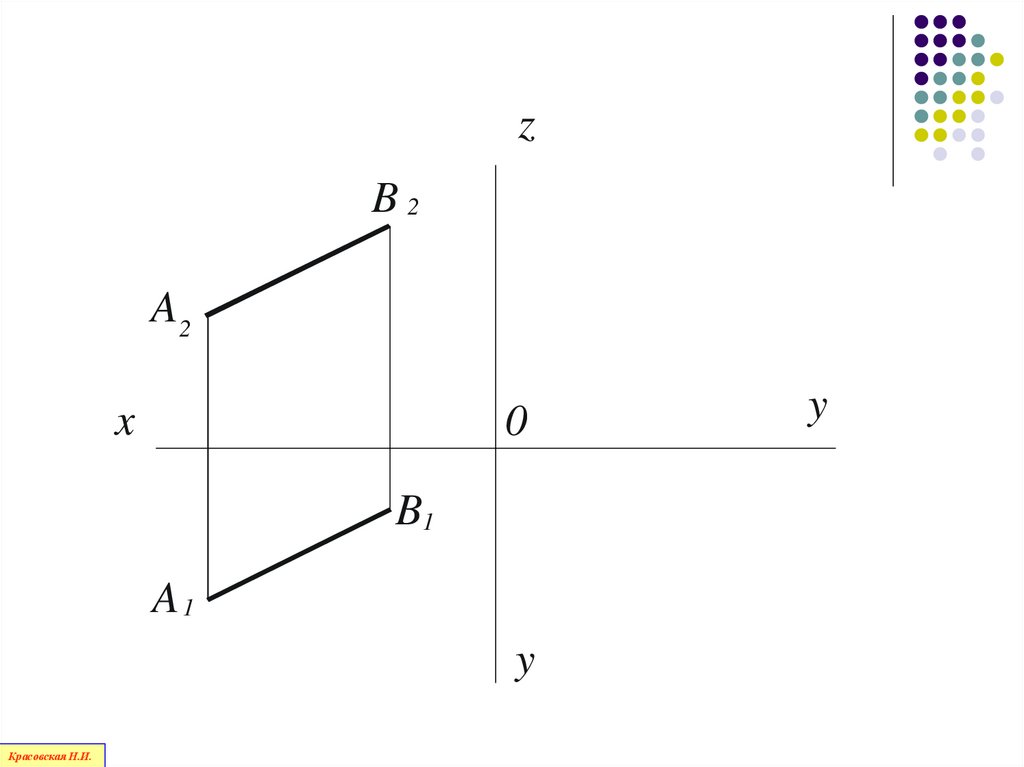
66.
zB2
A2
x
0
B1
A1
y
Красовская Н.И.
y
67.
Прямыечастного положения
Красовская Н.И.
68.
Прямые, параллельные илиперпендикулярные одной из плоскостей
проекций, называются
прямыми частного положения
Красовская Н.И.
69.
Прямые уровняКрасовская Н.И.
70.
Прямые, параллельные одной из плоскостейпроекций, называются
прямыми уровня
Красовская Н.И.
71.
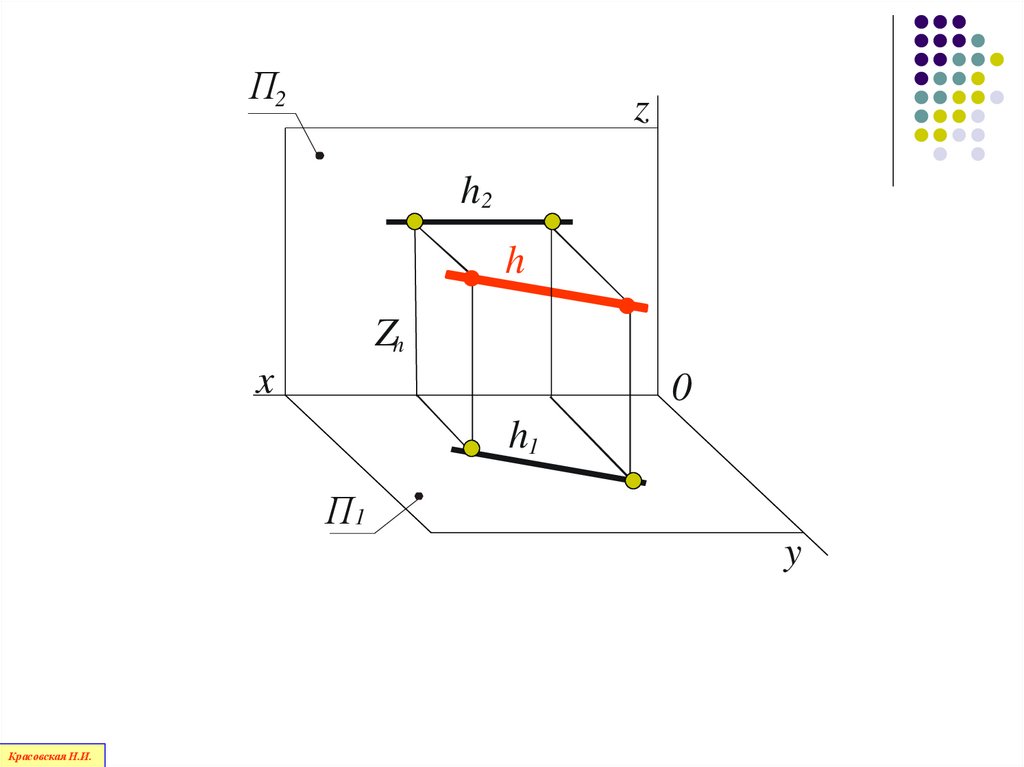
Прямая, параллельная горизонтальнойплоскости проекций П1, называется
горизонталью
Красовская Н.И.
72.
П2z
h2
h
Zh
x
0
h1
П1
y
Красовская Н.И.
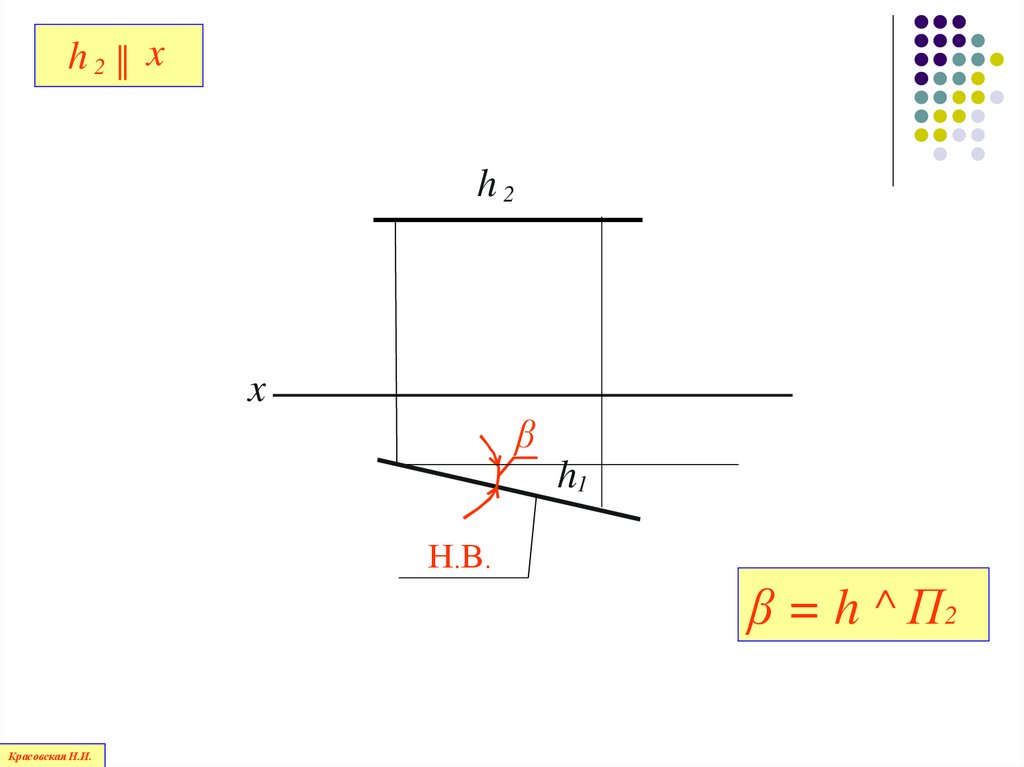
73.
h2║ xh2
x
β
h1
Н.В.
β = h ^ П2
Красовская Н.И.
74.
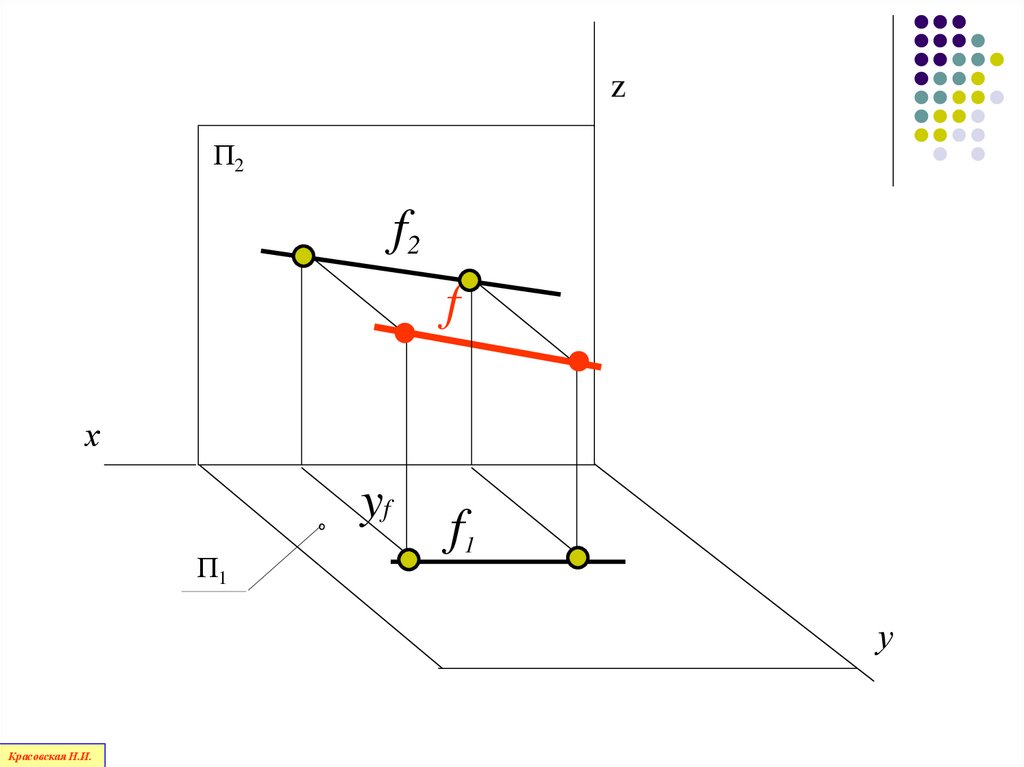
Прямая, параллельная фронтальнойплоскости проекций П2,
называется
фронталью
Красовская Н.И.
75.
zП2
f2
f
х
yf
П1
f1
у
Красовская Н.И.
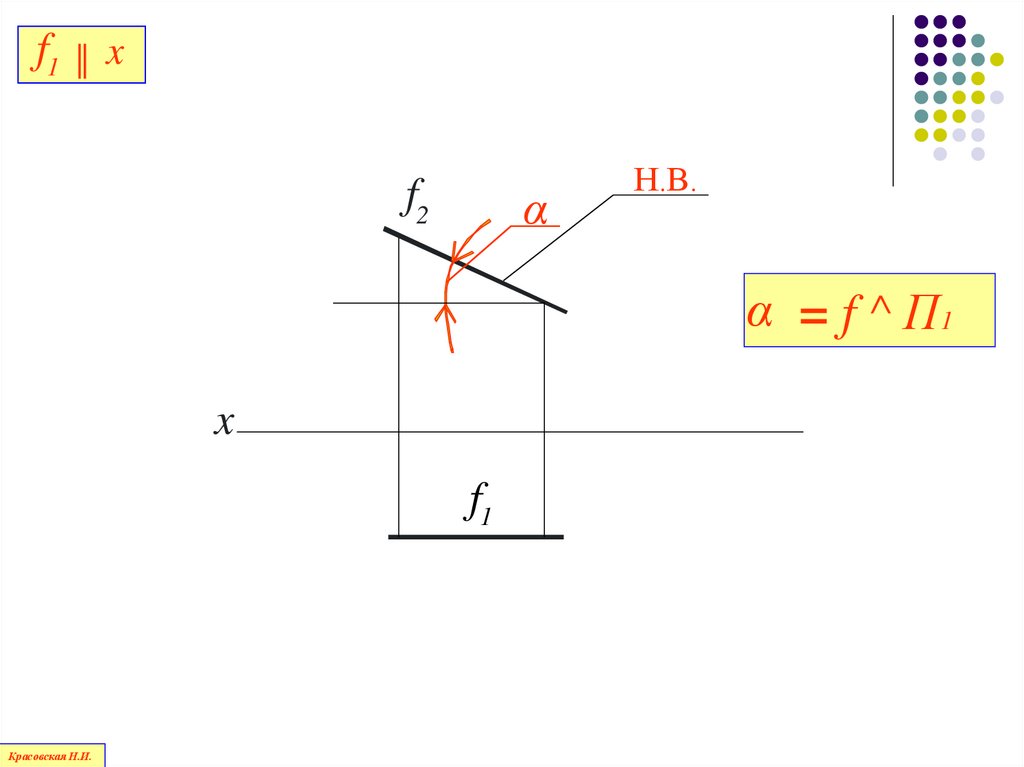
76.
f1 ║ xf2
α
Н.В.
α = f ^ П1
x
f1
Красовская Н.И.
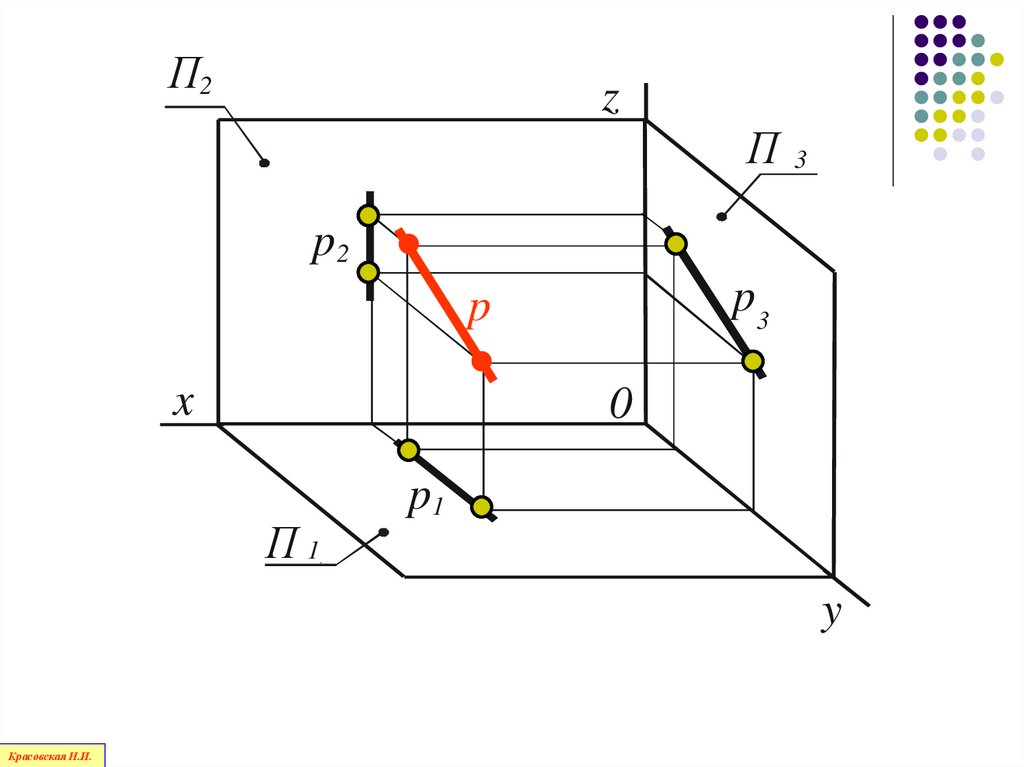
77.
Прямая, параллельная профильнойплоскости проекций П3, называется
профильной
прямой
Красовская Н.И.
78.
П2z
П
3
p2
p3
p
x
0
П1
p1
y
Красовская Н.И.
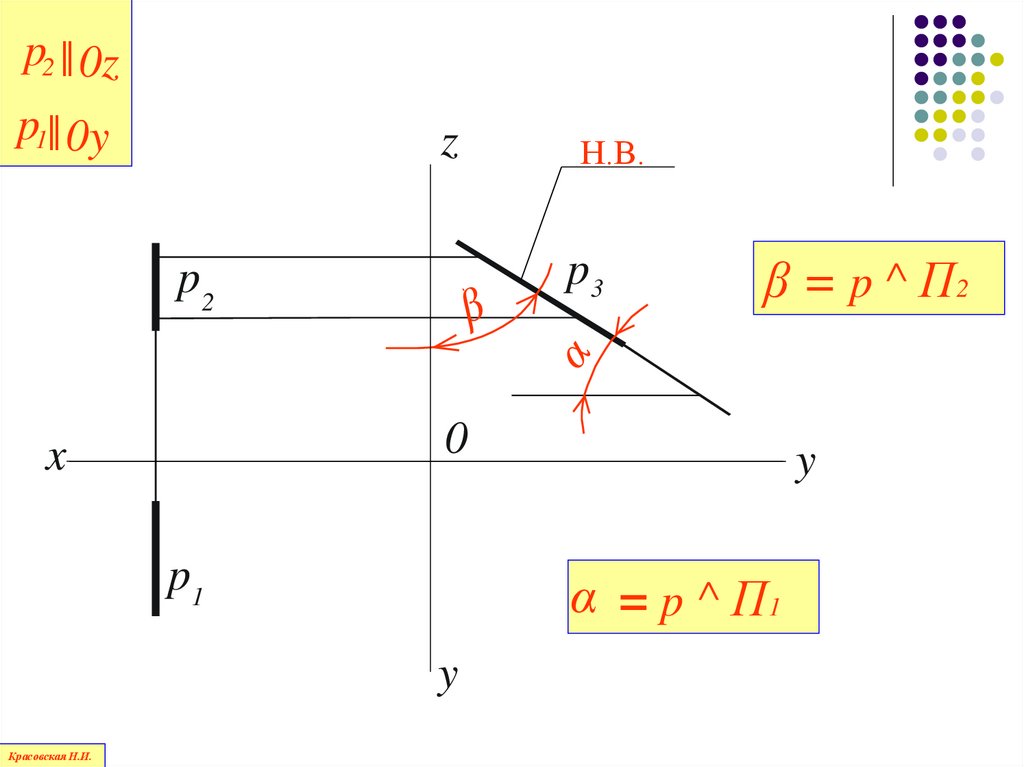
79.
p2 ║ 0zp1║ 0y
z
p3
p2
β = p ^ П2
0
x
p1
y
α = p ^ П1
y
Красовская Н.И.
Н.В.
80.
Проецирующиепрямые
Красовская Н.И.
81.
Прямые, перпендикулярные одной изплоскостей проекций, называются
проецирующими
Красовская Н.И.
82.
Прямая, перпендикулярная горизонтальнойплоскости проекций П1 –
горизонтально - проецирующая
прямая
Красовская Н.И.
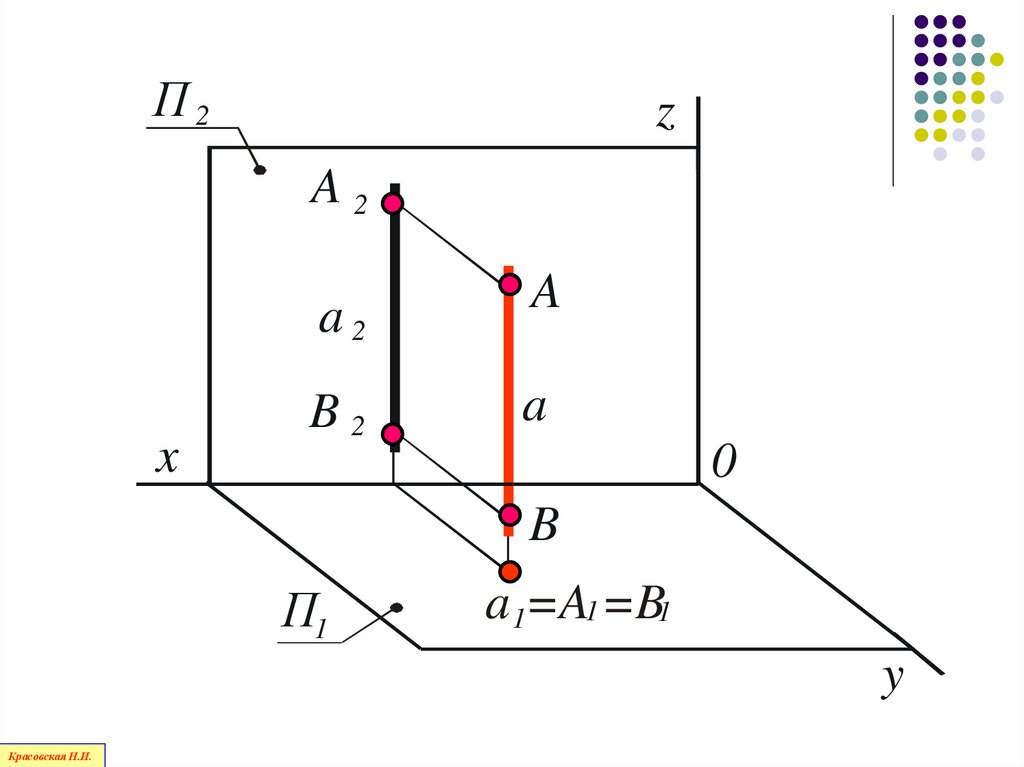
83.
П2z
A2
x
a2
A
B2
a
0
B
П1
a 1=A1 =B1
y
Красовская Н.И.
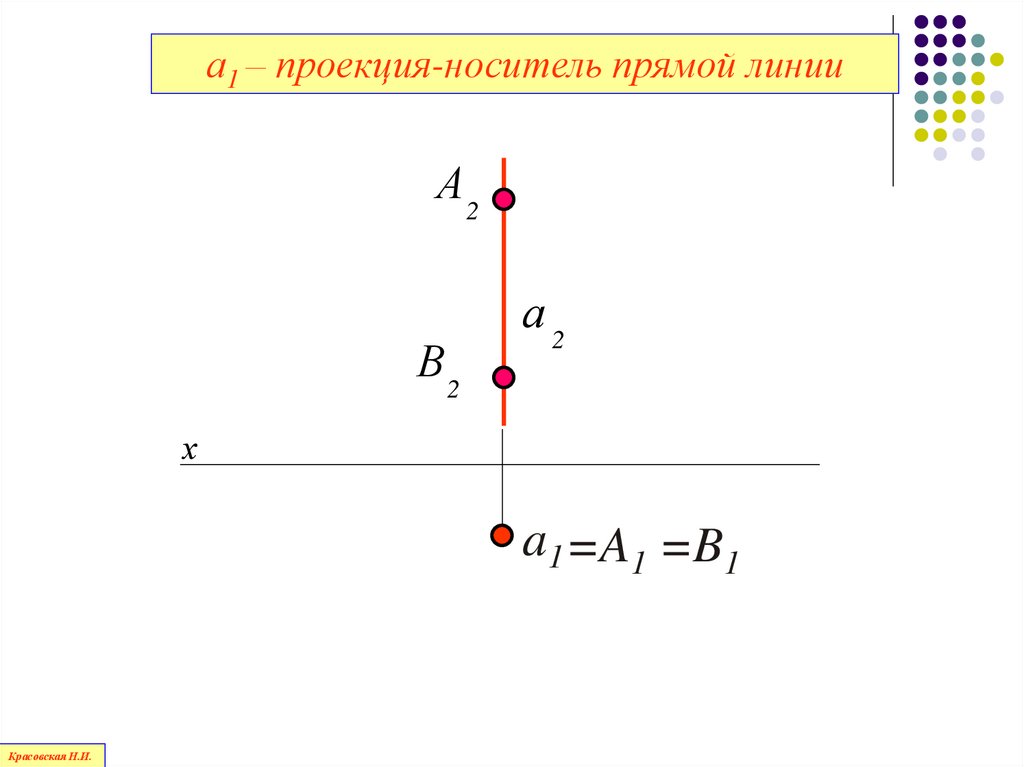
84.
а1 – проекция-носитель прямой линииА2
В2
а2
х
a1 =A1 =B1
Красовская Н.И.
85.
Проекция-носитель обладаетсобирательным свойством:
все точки, лежащие на проецирующей
прямой, проецируются в эту
проекцию-носитель
Красовская Н.И.
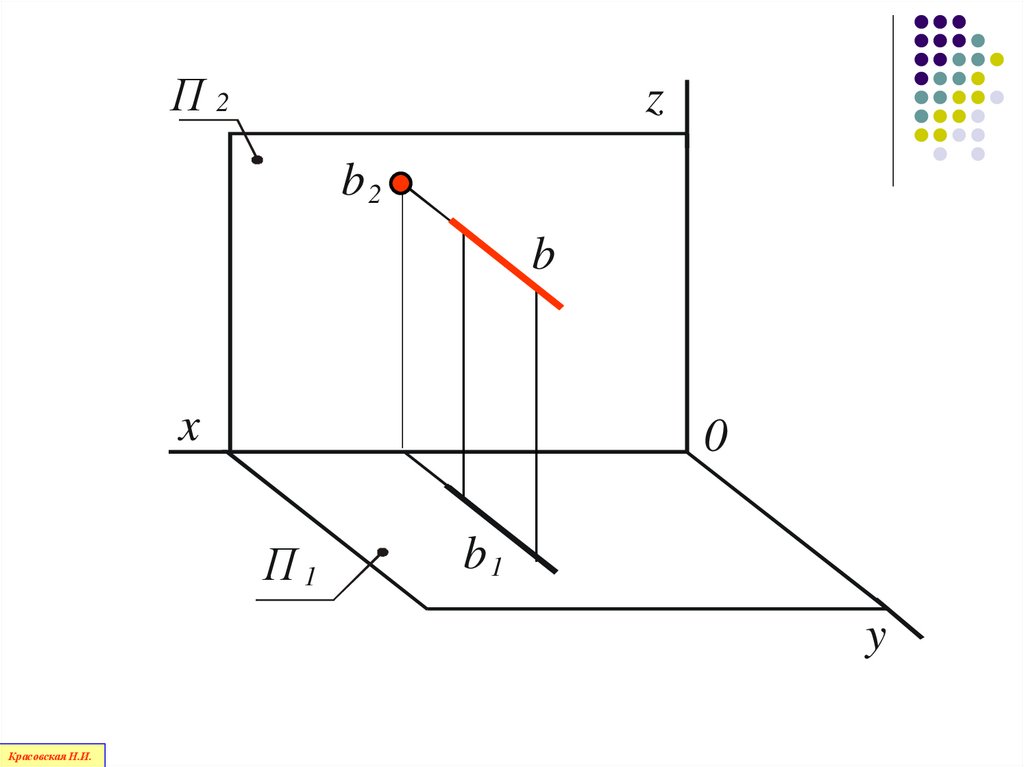
86.
Прямая, перпендикулярная фронтальнойплоскости проекций П2–
фронтально - проецирующая
прямая
Красовская Н.И.
87.
П2z
b2
b
x
0
П1
b1
y
Красовская Н.И.
88.
b2х
b1
Красовская Н.И.
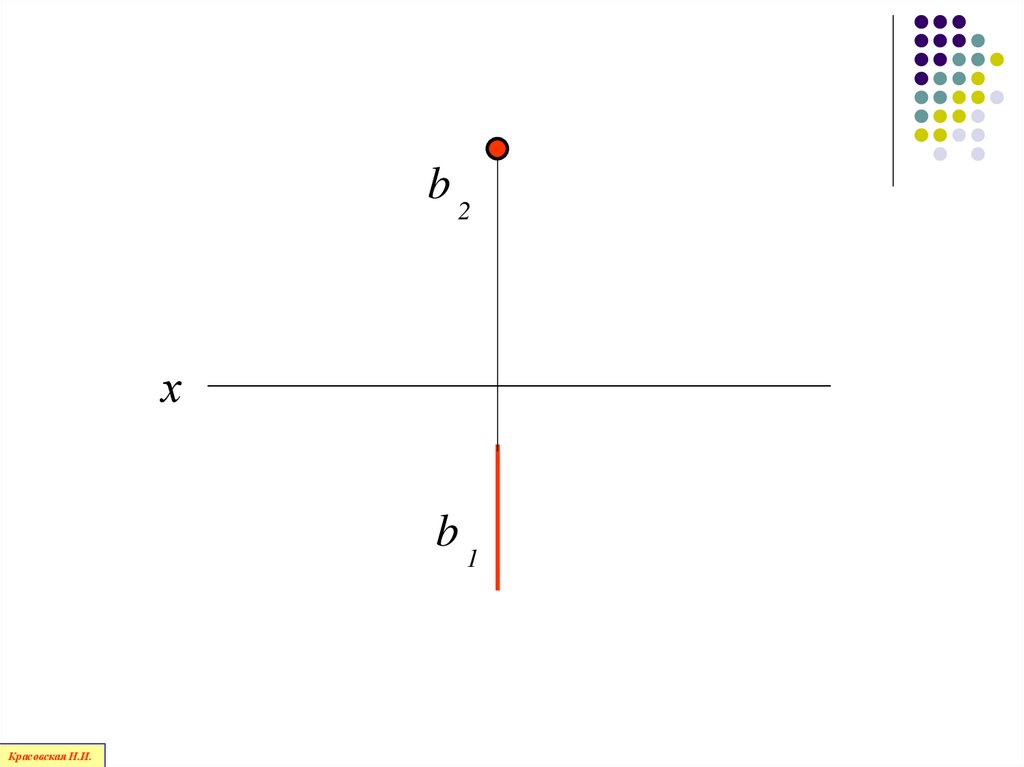
89.
Прямая, перпендикулярная профильнойплоскости проекций П3 –
профильно - проецирующая
прямая
Красовская Н.И.
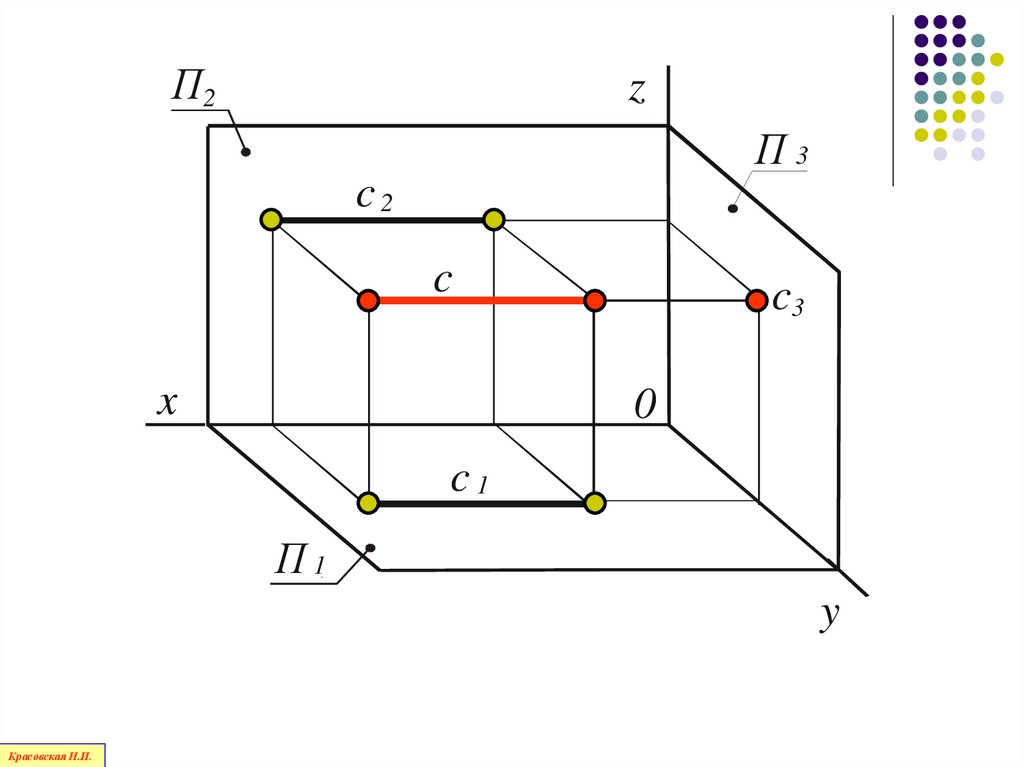
90.
П2z
П3
c2
c
x
c3
0
c1
П1
y
Красовская Н.И.
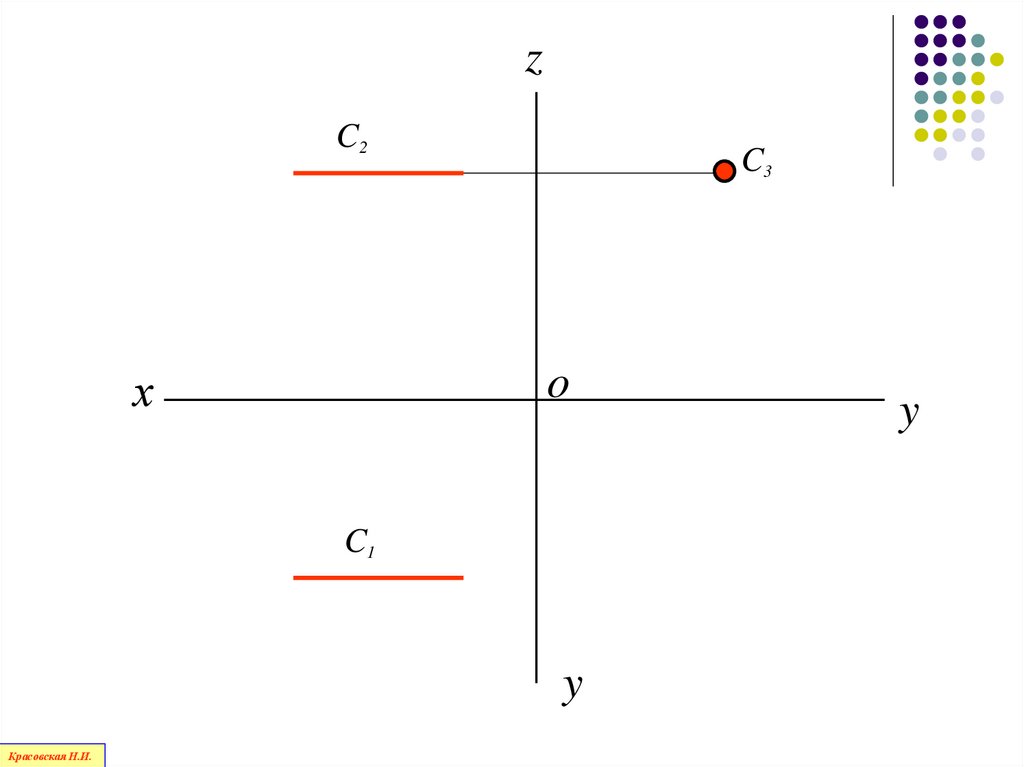
91.
zC2
х
C3
o
C1
y
Красовская Н.И.
y
92.
Точкана прямой
Красовская Н.И.
93.
Если точка в пространстве лежит напрямой,
то ее проекции лежат
на соответствующих проекциях
этой прямой
Красовская Н.И.
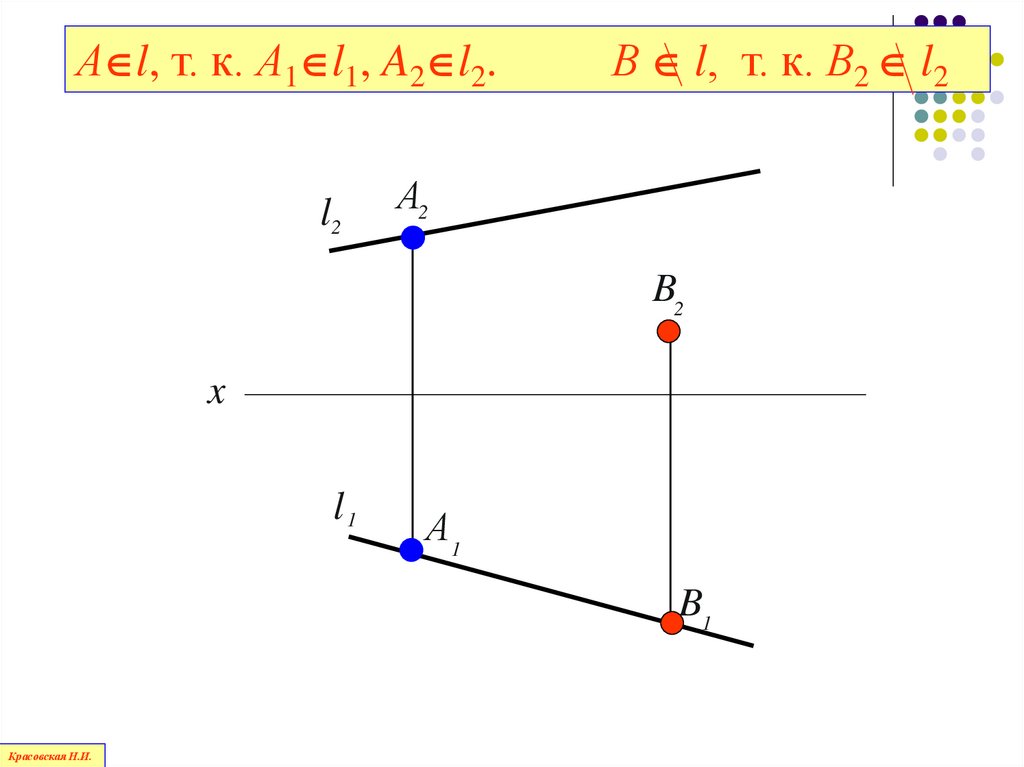
94.
А l, т. к. А1 l1, A2 l2.l2
В l, т. к. В2 l2
А2
B2
x
l1
А1
B1
Красовская Н.И.
95.
Взаимное положениепрямых
Красовская Н.И.
96.
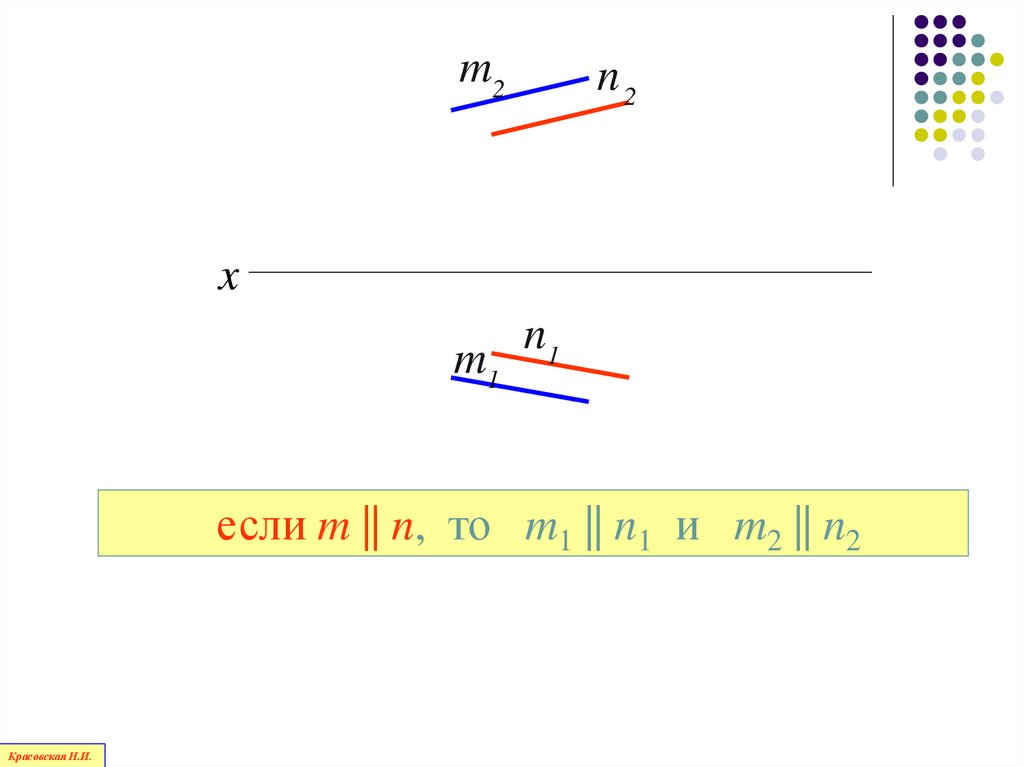
Проекции параллельныхпрямых параллельны
Красовская Н.И.
97.
m2n2
x
m1
n1
если m || n, то m1 || n1 и m2 || n2
Красовская Н.И.
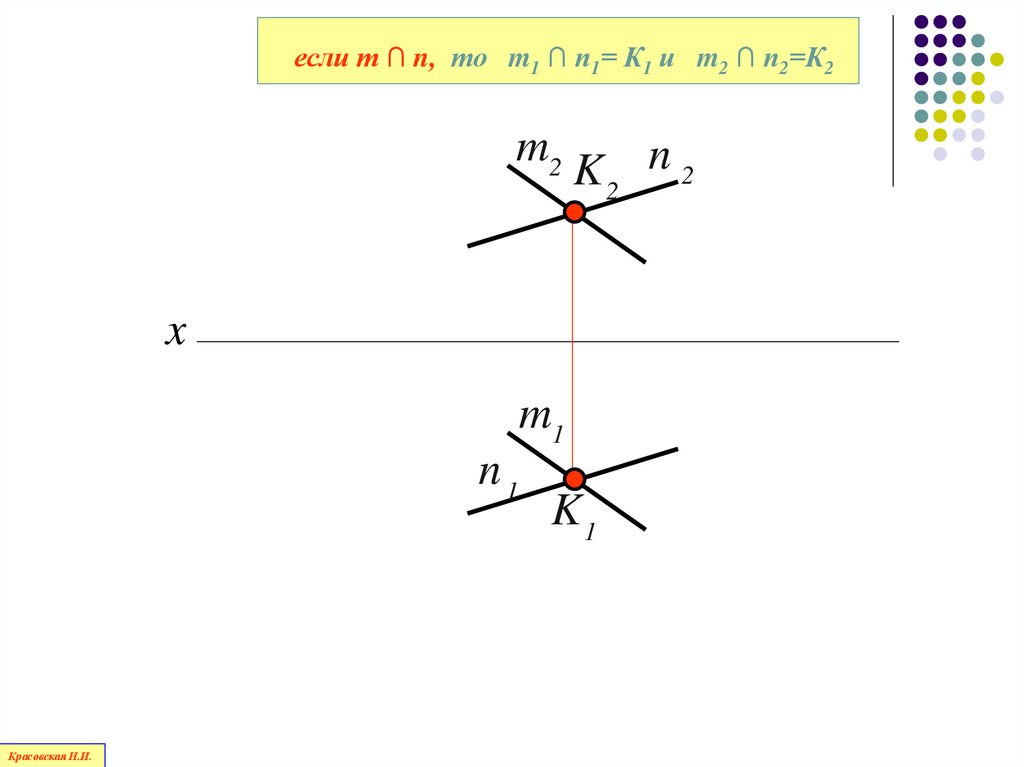
98.
Прямые линии,имеющие общую точку,
называются
пересекающимися
Красовская Н.И.
99.
если m ∩ n, то m1 ∩ n1= К1 и m2 ∩ n2=К2m2
K2 n 2
x
m1
n1
Красовская Н.И.
K1
100.
Не пересекающиесяи не параллельные между собой прямые,
называются
скрещивающимися
Красовская Н.И.
101.
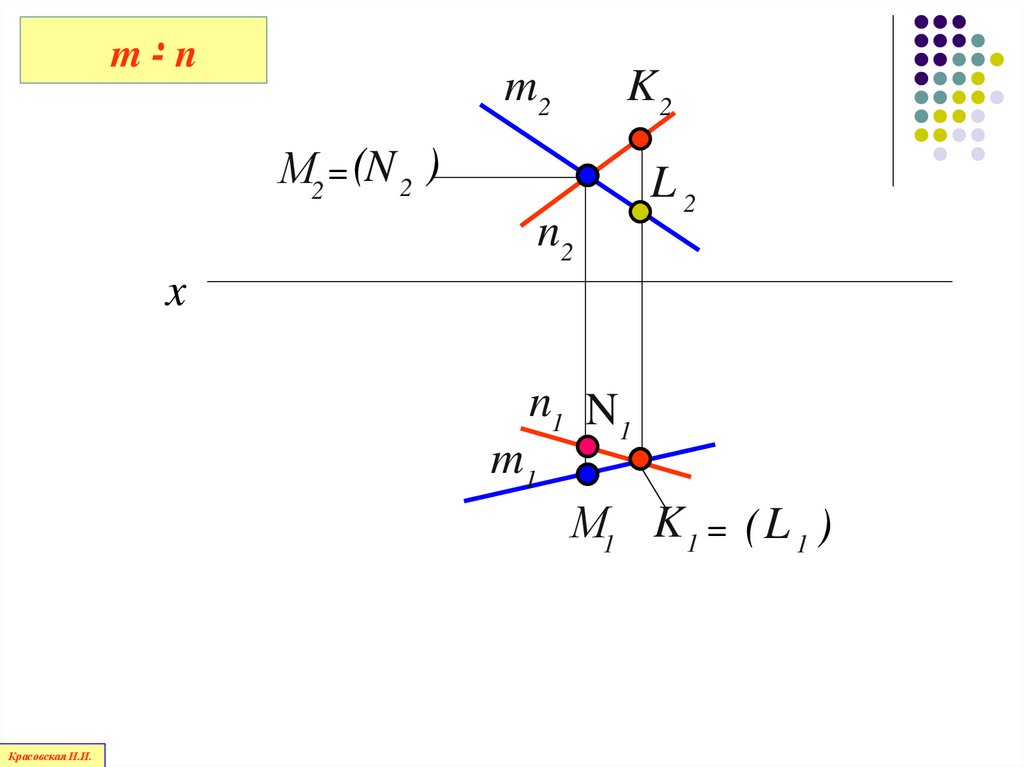
Точки пересечения проекцийскрещивающихся прямых являются
проекциями двух разных точек этих
прямых в пространстве
Эти точки называются
конкурирующими
Красовская Н.И.
102.
m-nm2
K2
М2 = (N 2 )
n2
L2
x
n1 N
1
m1
М1 K 1 = ( L 1 )
Красовская Н.И.
103.
Теоремао проекциях
прямого угла
Красовская Н.И.
104.
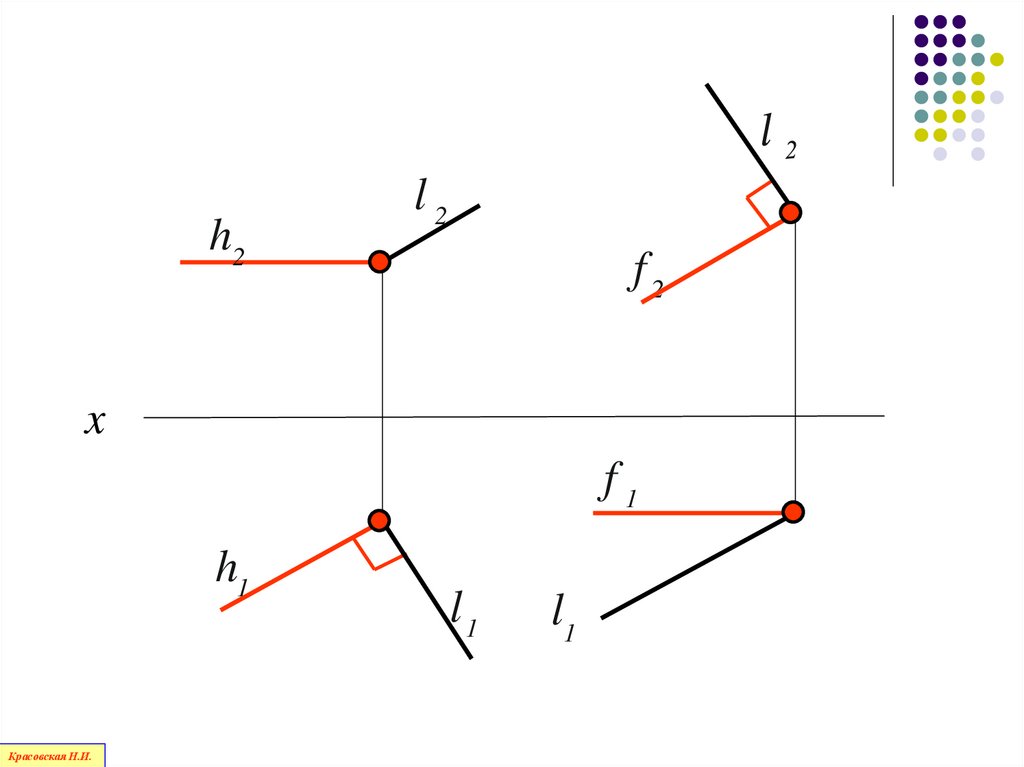
Если одна сторона прямого углапараллельна
плоскости проекций,
а другая ей не перпендикулярна,
то прямой угол
проецируется на эту плоскость
без искажения
Красовская Н.И.
105.
h2l2
f2
x
f1
h1
Красовская Н.И.
l1
l1
106.
Прямой угол можно построить на чертежебез искажения только
с натуральной величиной прямой уровня
Красовская Н.И.
107.
Кривые линииКрасовская Н.И.
108.
Кривая линияполучается
при движении точки
с изменением направления
Красовская Н.И.
109.
Закономерные кривые - это линии, законобразования которых известен
Незакономерные кривые - это линии, закон
образования которых не установлен
Циркульные кривые линии - линии,
кривизна которых постоянна
Лекальные кривые линии- линии,
кривизна которых непрерывно меняется
Красовская Н.И.
110.
Плоские кривыелинии
Красовская Н.И.
111.
Кривые линии,все точки которых принадлежат одной
плоскости, называются
плоскими
Красовская Н.И.
112.
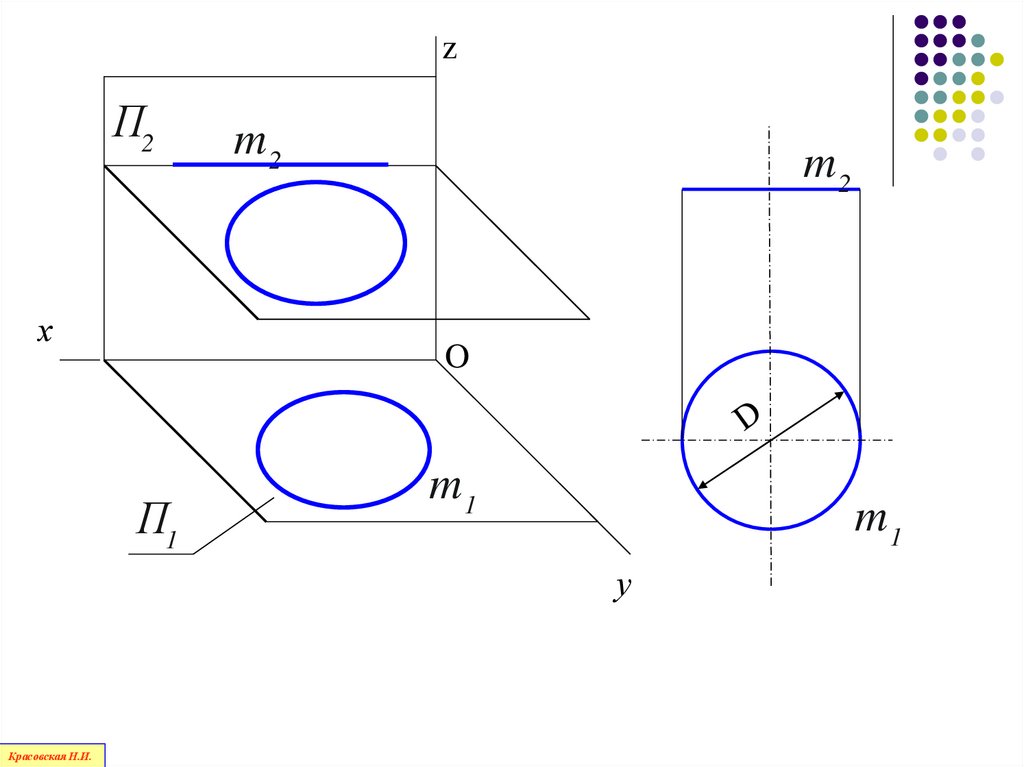
zП2
х
m2
m2
O
П1
m1
m1
у
Красовская Н.И.
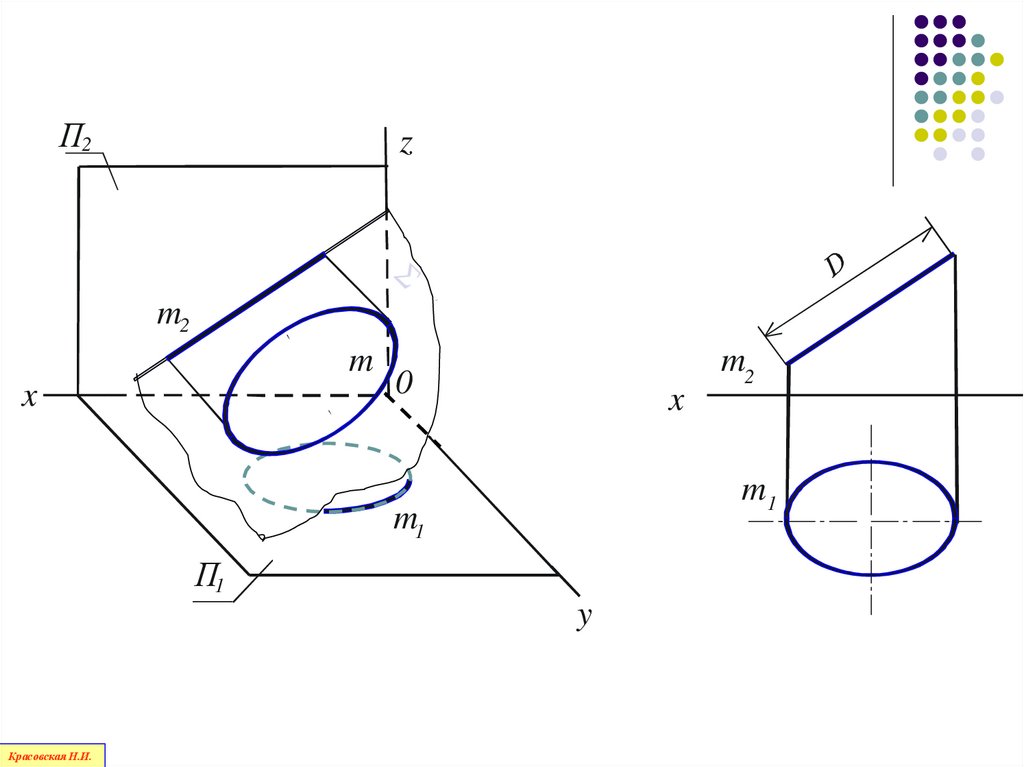
113.
П2z
m2
m
x
0
x
m1
m1
П1
y
Красовская Н.И.
m2
114.
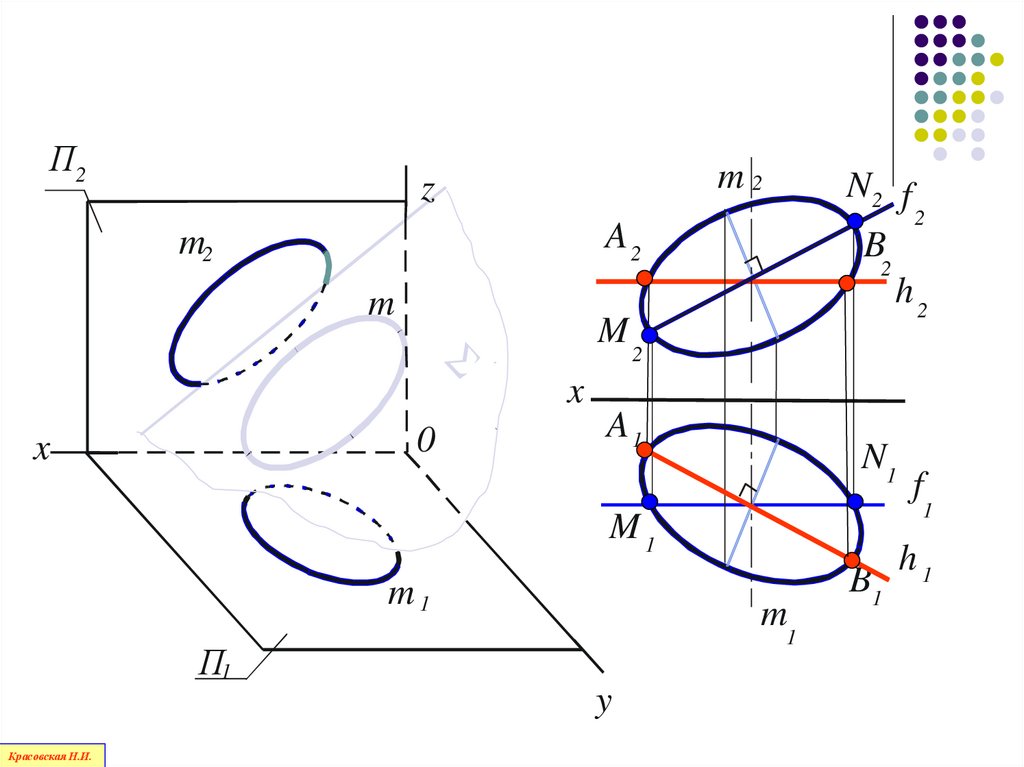
Большие оси эллипсов принадлежат линиям уровня,(соответственно
горизонтали h и фронтали f ),
и
по величине равны
диаметру окружности
Малые оси перпендикулярны
большим осям
Малые оси эллипсов в проекциях определяются
специальными построениями с помощью полухорд
Красовская Н.И.
115.
П2m2
z
N2 f
2
B
2
h2
A2
m2
m
M
2
x
0
x
A1
N1
1
M1
m1
m
1
П1
y
Красовская Н.И.
f
B1
h1
116.
Пространственныекривые
Красовская Н.И.
117.
Кривые линии,все точки которых
не принадлежат одной плоскости,
называются
пространственными
Красовская Н.И.
118.
Чтобы определить длину кривой линии,необходимо осуществить ее
спрямление
Красовская Н.И.
119.
Винтовые линииКрасовская Н.И.
120.
Винтовая линияпредставляет собой траекторию движения
точки,
равномерно вращающейся вокруг оси
и одновременно перемещающейся
с постоянной скоростью
вдоль этой оси
Цилиндрическую винтовую линию называют
гелисой
Красовская Н.И.
121.
Шагвинтовой линии –
это величина перемещения точки
в направлении оси, соответствующая
одному обороту
ее вокруг этой оси
Красовская Н.И.
122.
Винтовая линия может быть :левой,
если точка перемещается от наблюдателя,
вращаясь против часовой стрелки
правой,
если точка перемещается к наблюдателю,
вращаясь по часовой стрелке
Красовская Н.И.
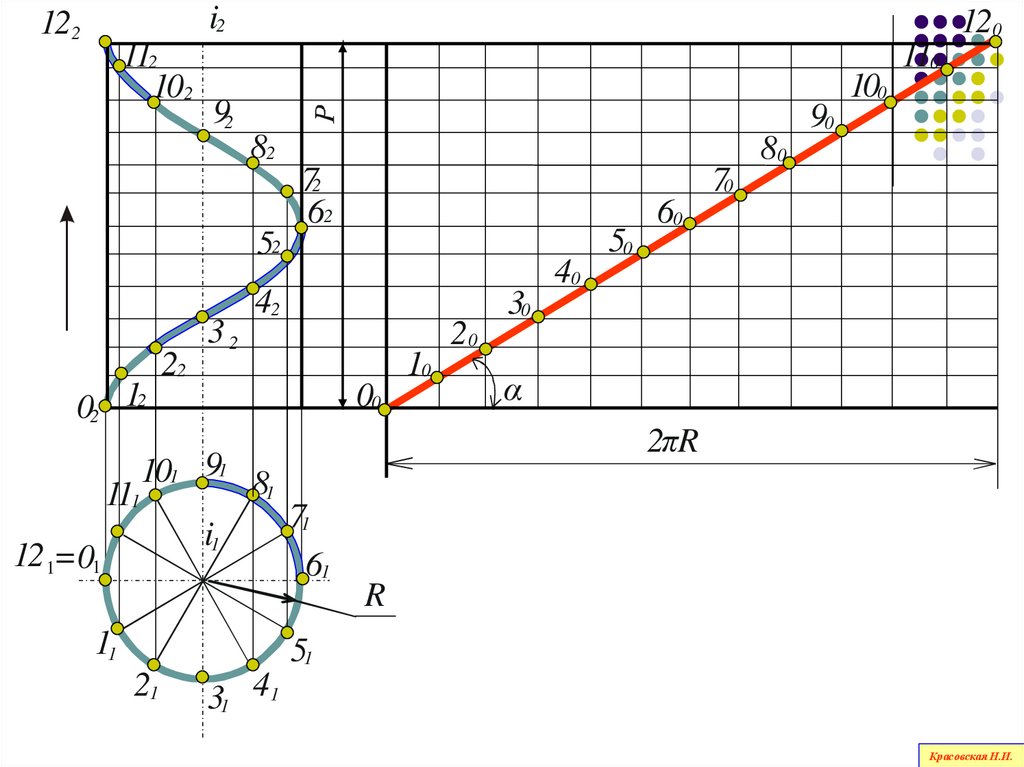
123.
На развертке цилиндрической поверхностивинтовая линия
изображается прямой,
являющейся гипотенузой прямоугольного
треугольника, у которого
один катет равен длине окружности основания
цилиндра (2 R),
другой равен шагу винтовой линии (Р)
Красовская Н.И.
124.
i2122
112
102
120
92
90
82
80
72
62
70
52
22
32
40
42
10
02 12
00
101 91 8
1
111
71
i1
12 1= 01
61
11
100
110
20
50
60
30
α
2πR
R
51
21
31 41
Красовская Н.И.
125.
ВЫВОДЫ- с кинематической точки зрения линию следует
рассматривать как траекторию непрерывно
движущейся в пространстве точки
-линия на чертеже может быть задана
двумя ее проекциями
- по расположению проекций линии можно
однозначно судить
об ее положении в пространстве
Красовская Н.И.
126.
ЗадачаПостроить три
проекции точки А
с координатами
А(20,0,40)
Н.И.Красовская
127.
ЗадачаЗадать горизонталь длиной 50 мм, расположенной от П1 на расстоянии
20мм и под углом к П2 45о
х
Красовская Н.И.





















































































 Инженерная графика
Инженерная графика








