Похожие презентации:
Начертательная геометрия. Плоскость. Главные линии плоскости
1.
Начертательная геометрияНаправление : 35.03.06 | Агроинженерия
Направленность: Технические системы в агробизнесе
Лекция 3: Плоскость. Главные линии плоскости.
Взаимное расположение точки и плоскости.
Взаимное расположение прямой линии и плоскости.
КубГАУ, 2021 г.
2.
'ПЛОСКОСТЬ
Задание и изображение на чертеже
Положение плоскости в пространстве и на чертеже можно определить:
1) тремя точками, не лежащими на одной прямой;
2) прямой и точкой вне ее;
3) двумя пересекающимися прямыми;
4) двумя параллельными прямыми;
5) любой плоской фигурой;
6) следами.
Следом плоскости называется линия пересечения этой плоскости с плоскостями проекций.
Горизонтальный след PП1; фронтальный PП2
Плоскость, не перпендикулярная ни одной плоскости проекций, называется плоскостью общего
положения. На комплексном чертеже проекции элементов, задающих плоскость, занимают общее
положение.
Плоскость, перпендикулярная или параллельная одной из плоскостей проекций, называется
B2
плоскостью частного положения.
C2
A2
B2
a2
A2
a2
b2
b2
C1
A1
b1
C
A1
a1
A1
B1
1)
a1
a1
B1
b1
2)
C2
A2
a2
3)
4)
6).
5)
PП2
Px
PП1
3.
РАЗЛИЧНЫЕ ПОЛОЖЕНИЯ ПЛОСКОСТЕЙОТНОСИТЕЛЬНО ПЛОСКОСТЕЙ ПРОЕКЦИЙ
Проецирующая плоскость
Плоскость, перпендикулярная одной из плоскостей проекций, называется проецирующей.
Различают:
a) горизонтально проецирующая плоскость (a ^ П1 ); б) фронтально проецирующая плоскость
b) (b ^ П2);
в) профильно-проецирующая плоскость (g ^ П3).
У проецирующих плоскостей одна проекция вырождается в прямую. Поэтому проекция фигуры,
принадлежащей такой плоскости (треугольник ABC), вырождается в прямую (A1B1C1).
Проецирующая плоскость однозначно задается на чертеже своей линейной проекцией или z
проецирующим следом плоскости( Рп1 Рп2 Рп3)
a2
в)
B2
П2
РП2
C2
A2
РП1
x
j A
1
р
B1
y
C1
а)
x
a1
b1
B
B1
П
l
РП2
C
A
x Рх
A1
b3
b2
b ≡РП2
x
C1
РП1
b1
a3
a1
б)
4.
ПЛОСКОСТЬ УРОВНЯПлоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.
П2
B2
A2
C2 QП2
Различают:
а) горизонтальная плоскость
уровня (QП2// П1);
б) фронтальная плоскость
уровня (RП1 // П2);
в) профильная плоскость
уровня (TП2 // П3).
Плоскость уровня является частным случаем проецирующей
плоскости, поэтому на чертеже
задается своей линейной проекцией или собирательным следом
Фигура, принадлежащая плоскости
уровня, проецируется на соответствующую плоскость проекций в
натуральную величину.
B
A
C
Q
x
B1
A1
A
C12
П1
QП2
B2
C2
а)
x
B1
A1
C1
П2
a2
b2
x
Rп1
а1≡b1≡ Rп1
x
Тп2
Тп2
Тх
Т
Тп1
б)
Тх
x
П1
Тп1
в)
5.
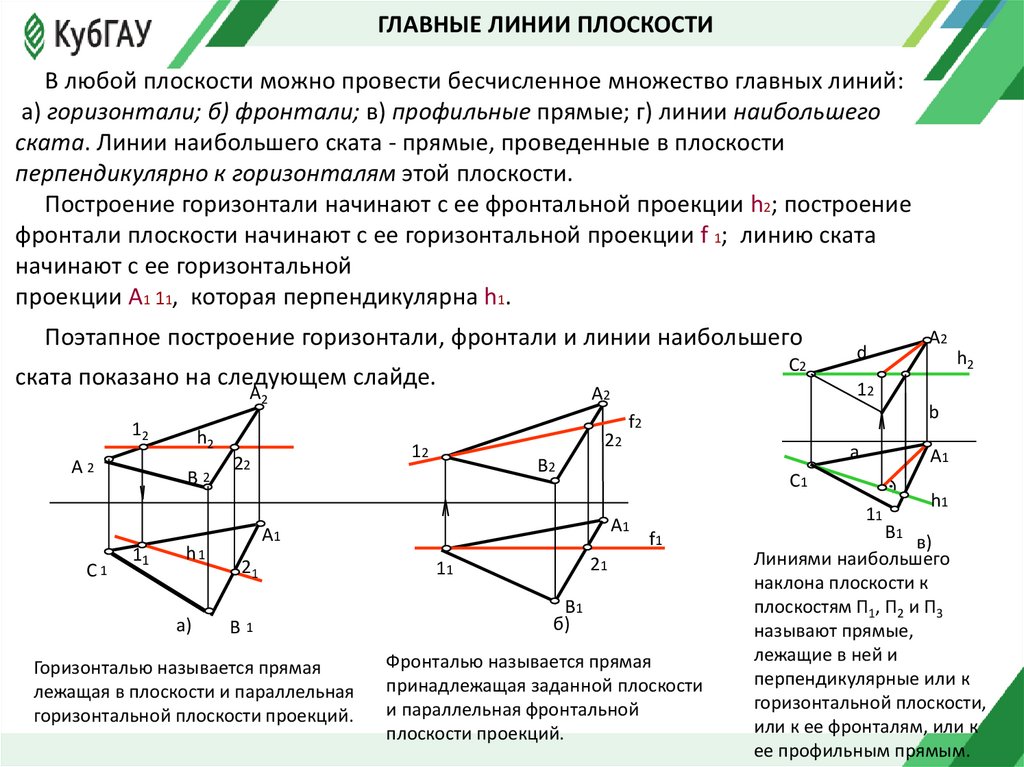
ГЛАВНЫЕ ЛИНИИ ПЛОСКОСТИВ любой плоскости можно провести бесчисленное множество главных линий:
а) горизонтали; б) фронтали; в) профильные прямые; г) линии наибольшего
ската. Линии наибольшего ската - прямые, проведенные в плоскости
перпендикулярно к горизонталям этой плоскости.
Построение горизонтали начинают с ее фронтальной проекции h2; построение
фронтали плоскости начинают с ее горизонтальной проекции f 1; линию ската
начинают с ее горизонтальной
проекции A1 11, которая перпендикулярна h1.
Поэтапное построение горизонтали, фронтали и линии наибольшего
С2
ската показано на следующем слайде.
A2
12
А2
С1
h2
В
11
2
h1
а)
22
21
В1
Горизонталью называется прямая
лежащая в плоскости и параллельная
горизонтальной плоскости проекций.
a
A1
С1
A1
11
f1
21
11
h2
b
f2
В2
A1
A2
12
A2
22
12
d
В1
б)
Фронталью называется прямая
принадлежащая заданной плоскости
и параллельная фронтальной
плоскости проекций.
h1
В1
в)
Линиями наибольшего
наклона плоскости к
плоскостям П1, П2 и П3
называют прямые,
лежащие в ней и
перпендикулярные или к
горизонтальной плоскости,
или к ее фронталям, или к
ее профильным прямым.
6.
ПОЭТАПНОЕ ПОСТРОЕНИЕ ГЛАВНЫХ ЛИНИЙ ПЛОСКОСТИA2
A2
a2
12
h2
С2
С1
В2
11
С2
a1
С1
a2
h2
В2
A1
11
A2
12
В2
A1
21
С2
22
12
22
h1
f2
a1
f1
A1
С1
21
h1
11
В1
А2
а)
В1
В1
б)
г)
7.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ТОЧКИ И ПЛОСКОСТИТочка лежит в плоскости, если ее проекции находятся на одноименных проекциях
какой-либо прямой, принадлежащей данной плоскости.
Произвольно выбирают одну проекцию точки M, например, фронтальную ее проекцию M2 .
Искомую горизонтальную проекцию M1 точки M находят по линиям связи на горизонтальной
проекции (A1 11) прямой A1 плоскости. Таких вспомогательных прямых в плоскости можно
провести через точку M бесчисленное множество. Одна из них и представлена на эпюре.
Если взять точку K горизонтально конкурирующую
K2
с точкой M и расположенную над ней, то точка K
B2
будет расположена и над плоскостью.
M
12
2
A2
C2
∆z
С2
A2
d
h 32
12
22
B
b
A1
∆z
a
A
M1__ K1
1
C
С1
h1
31
α
21
А0
11
В1
8.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ ЛИНИИ И ПЛОСКОСТИВозможны следующие три случая относительного расположения прямой и плоскости:
прямая принадлежит плоскости, прямая параллельна плоскости, прямая пересекает
плоскость.
На основании свойства плоскости: если прямая линия соединяет две точки данной
плоскости, то такая прямая всеми своими точками лежит в этой плоскости. Построение
прямых, принадлежащих плоскости рассмотрены на слайде (главные линии плоскости).
B2
K2
K2
a2
C2
m2
m2
A2
B1
K1
K1
a
m1
A1
m1
' C1
Из стереометрии известно: если
прямая параллельна плоскости,
то она параллельна одной из
прямых, лежащих в этой
плоскости. На эпюре
параллельность прямой m и
плоскости ABC
доказывается тем, что m2 // a2, m1
// a1 ; прямая принадлежит
плоскости ABC.
9.
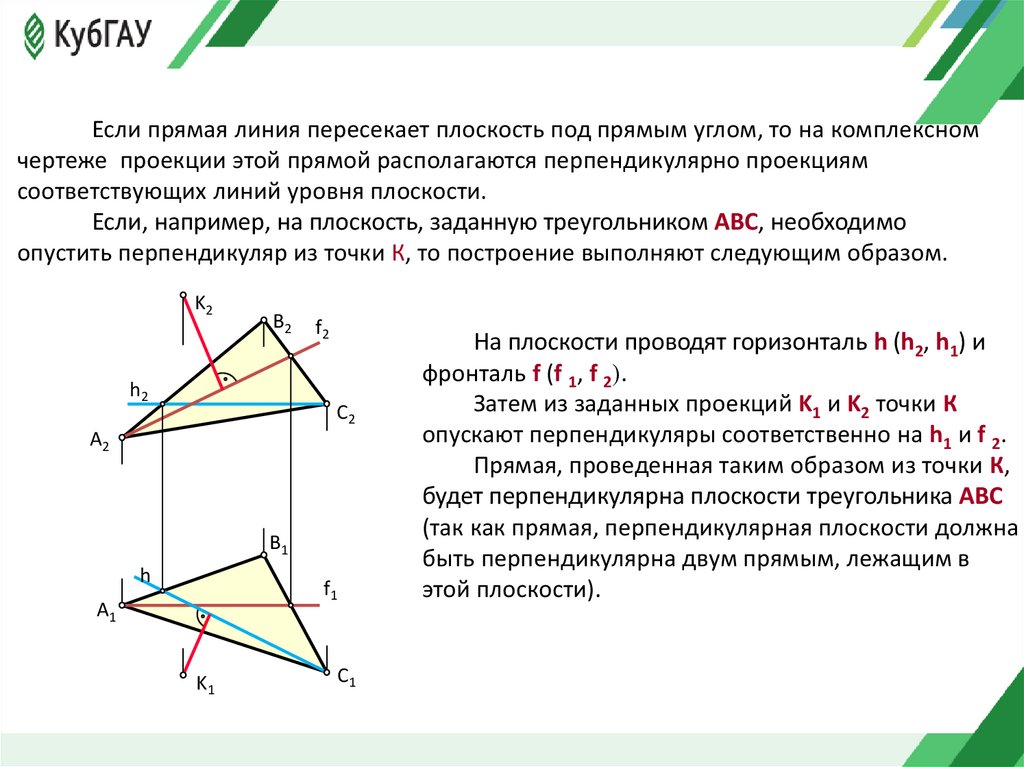
Если прямая линия пересекает плоскость под прямым углом, то на комплексномчертеже проекции этой прямой располагаются перпендикулярно проекциям
соответствующих линий уровня плоскости.
Если, например, на плоскость, заданную треугольником ABC, необходимо
опустить перпендикуляр из точки К, то построение выполняют следующим образом.
K2
B2
h2
f2
C2
A2
B1
h
f1
A1
K1
C1
На плоскости проводят горизонталь h (h2, h1) и
фронталь f (f 1, f 2).
Затем из заданных проекций K1 и K2 точки К
опускают перпендикуляры соответственно на h1 и f 2.
Прямая, проведенная таким образом из точки К,
будет перпендикулярна плоскости треугольника ABC
(так как прямая, перпендикулярная плоскости должна
быть перпендикулярна двум прямым, лежащим в
этой плоскости).
10.
ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ДВУХ ПЛОСКОСТЕЙДве плоскости в пространстве могут быть либо взаимно параллельными, либо
пересекающимися.
Плоскости параллельны, если две пересекающиеся прямые одной плоскости
соответственно параллельны двум пересекающимся прямым другой плоскости.
Искомая плоскость b, параллельная заданной плоскости a, определена
прямыми a1 и b1 соответственно параллельными a и b заданной плоскости и
проходящими через произвольную точку пространства A.
b2
b2
A2
a2
a2
a1
a1
b1
b1
A1
11.
Определение линии пересечения двух плоскостей общего положенияДля определения точек линии пересечения обе заданные плоскости a и b
пересекают двумя вспомогательными (параллельными между собой) плоскостямипосредниками. Некоторое упрощение можно достичь, если вспомогательные
плоскости проводить через прямые, задающие плоскость.
Рассмотрим пример. Плоскость a задана (ABC), плоскость b задана (DEK). Точки M
и N, определяющие искомую линию пересечения двух данных плоскостей найдем как
точки пересечения каких-либо двух сторон (как две прямые) треугольника ABC с
плоскостью другого треугольника DEK, т.е. дважды решим позиционную задачу на
определение точки пересечения прямой с плоскостью по рассмотренному алгоритму.
Выбор сторон треугольников произволен, так как только построением можно
точно определить, какая действительно сторона и какого треугольника пересечет
плоскость другого. Выбор плоскости-посредника также произволен, так как прямую
общего положения, какими являются все стороны треугольников ABC и DEK, можно
заключить в горизонтально проецирующую или во фронтально проецирующую
плоскости.
12.
ZB2
П2
C2
N2
D2
M2
E2
A2
B
K2
O
D
M
X
E
N
C
A
K
K1
B1
M1
C1
П1
E1
A1
N1
D1
Y
Здесь вы видите аксонометрическое изображение решения задачи на
определение линии MN пересечения двух плоскостей ABC и DEK.
13.
D212
32
Для построения точки M использована горизонтально
проецирующая плоскость - посредник a (a1), в которую
заключена сторона AB треугольника ABC (AB Ì a).
42
M2
N2
E2
82
_
_7
62 _
2
2-й этап решения.
C2
Строим линию пересечения (на чертеже она задана
точками 1 и 2) плоскости-посредника a (a1) и плоскости DEK.
52
3-й этап решения.
A2
E1
1-й этап решения
B2
22
K2
B1
71
21
K1
M1
11
61
A1
a1
b1
N1
_
_
41_ 81
31
D1
C1
Находим точку M пересечения прямой 1 - 2 с прямой AB.
Найдена одна точка M искомой линии пересечения.
Для построения точки N использована горизонтально
проецирующая плоскость b (b1), в которую заключена сторона
AC треугольника ABC.
Построение аналогичны предыдущим. одна точка M
искомой линии пересечения.
Определение видимости на плоскости П1 выполнено с
помощью горизонтально конкурирующих точек 4 и 8 (41 º81).
Точка 4 расположена над точкой 8 (42 и 82), поэтому на
плоскости П1 часть треугольника DEK, расположенная в сторону
точки 4, закрывает собой часть треугольника ABC,
расположенную от линии пересечения в сторону точки 8.
С помощью пары фронтально конкурирующих точек 6 и 7
(62 º72) определена видимость на плоскости П2.
14.
Пересекающиеся плоскости.B2
РП2
12
22
C2
A2
11
A1
B1
a
21
C1
Линией пересечения двух плоскостей
является прямая, для построения которой
достаточно определить две точки, общие
обеим плоскостям.
Если
одна
из
пересекающихся
плоскостей занимает частное положение, то
ее вырожденная проекция (след плоскости)
включает в себя и проекцию линии a
пересечения плоскостей.
Горизонтальную проекцию прямой
строят по двум общим с плоскостью точкам
11 и 21. На горизонтальной проекции часть
∆ 11,А1,21 будет не видима, т.к находится
ниже проецирующего следа РП1.
15.
ПОСТРОИТЬ ЛИНИЮ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙN2
С2
K2
12
А2
42
22
62
F2
D2
L2
Pπ2
32
52
Qπ2
В2
E2
Х
0
K1
N1
L1
11
С1
В1
D1
21
31
51
E1
41
А1
61
F1
16.
АЛГОРИТМ ПОСТРОЕНИЯ ЛИНИИ ПЕРЕСЕЧЕНИЯ ПЛОСКОСТЕЙ:1. Для решения задачи воспользуемся двумя вспомогательными секущими
плоскостями уровня.
2. Определяем линию пересечения первой вспомогательной плоскости Рп1 с
заданными плоскостями ( АВ и СD; и ∆ЕNF) там, где на горизонтальной проекции эти 2
линии между собой пересекаются, находим точку К1 – общую для трех плоскостей.
Фронтальная проекция точки К лежит на фронтальном следе плоскости Рп2 .
3. Со второй секущей плоскостью Qп2 делаем аналогичные построения. Находим
общую точку для трех плоскостей К1\ ; К2\ . Одноименные проекции точек соединяем.
17.
ПОСТРОЕНИЕ ТОЧКИ ВСТРЕЧИ ПРЯМОЙ С ПЛОСКОСТЬЮ(2-Я ОСНОВНАЯ ЗАДАЧА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ)
Если плоскость задается частного положения и требуется определить точку встречи
прямой с плоскостью, необходимо вспомнить о собирательном свойстве одного из
следов плоскости. А согласно этому свойству точка встречи всегда лежит на
собирательном следе. Значит остается найти вторую проекцию точки встречи.
А2
А2
1)
х
к2
Рх
В2
Pп1
0 х
к1
Pп1
3)
0
В1
Рп1
к1
А1
С2
к2
В2
2)
В1
А1
D2
к2
х
В2
А2
E2
0
А1
D1
С1
E1
к1
В1
Если задана плоскость общего положения и прямая, то для нахождения точки
пересечения прямой с плоскостью необходимо сделать следующие построения:
1) заключить прямую в плоскость частного положения;
2) Построить линию пересечения заданной плоскости со вспомогательной;
3) Определить точку пересечения прямой с плоскостью;
4) Определить видимость прямой.
18.
Пример 1. Преобразоватьметодом замены плоскостей
эпюр таким образом, чтобы
плоскость общего положения
стала проецирующей (частного
положения).
12
Пример 2. Определить точку
встречи прямой с плоскостью
общего положения.
Рп2
А2
Рп2
12
П2 Рх
х П1
11
П2
х П1
0
Рх
11
А2
В2
=
0
А1 В1
Рп4
14
Рп1
Рх '
А1
Рп1
В4
Рх 1' 4
к4
А4
Рп4
19.
ОПРЕДЕЛЕНИЕ РАССТОЯНИЯ ОТ ТОЧКИ ДО ПЛОСКОСТИ.( 3-Я ОСНОВНАЯ ЗАДАЧА НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ).
Если плоскость до которой определяем расстояние является плоскостью частного
положения, задача решается очень просто.
Собирательное свойство плоскости частного положения дает нам возможность сразу
определить на следе точку пересечения перпендикуляра, опущенного из точки к
собирательному следу плоскости. Вторая проекция точки встречи находится по линии
проекционной связи.
Опустить перпендикуляр к плоскости заданной следами, это значит провести его на
проекциях перпендикулярно соответствующим следам плоскости(согласно теореме о
проекции прямого угла).
Если плоскость частного положения задана треугольником или любым другим
способом, перпендикуляр из точки нужно проводить на той проекции где треугольник или
другой геометрический образ проецировался в одну линию. Определим точку «К», а на
второй проекции перпендикуляр, проведенный из точки «К» будет всегда оси ох, т.к. на
первой проекции он проецируется в натуральную величину.
Если задается плоскость общего положения до которой нужно определить
расстояние, нужно преобразовывать эпюр таким образом, чтобы эта плоскость стала
проецирующей, а затем решать, как примеры 1, 2, 3
20.
Определение расстояние от точки А до частного положения плоскостиРп2
1)
Рх
х
А2
D2
А2
А2
К2
х
К1
А1
С2 В2
2)
D1
Рп2
К2
К2
х
А1
В1
К1
С1
Рп1
н.в.
3)
А1
К1
21.
ВИДИМОСТЬ КОНКУРИРУЮЩИХ ТОЧЕКС2
S2
D2 1 32
2
52
А2
к2
42
22
E2
Рп2
В2
х
А1
11
31
D1
S1
E1
41 51
С1
к1
21
В1
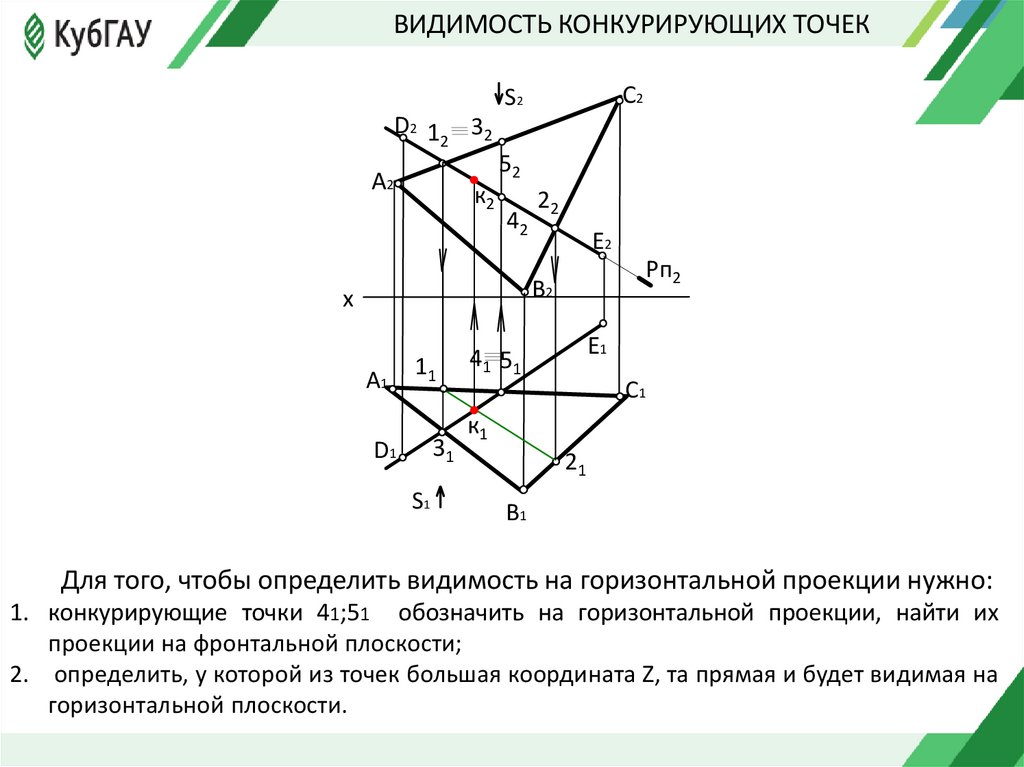
Для того, чтобы определить видимость на горизонтальной проекции нужно:
1. конкурирующие точки 41;51 обозначить на горизонтальной проекции, найти их
проекции на фронтальной плоскости;
2. определить, у которой из точек большая координата Z, та прямая и будет видимая на
горизонтальной плоскости.
22.
ОПРЕДЕЛЕНИЕ РАССТОЯНИЕ ОТ ТОЧКИ А ДОПЛОСКОСТИ ОБЩЕГО ПОЛОЖЕНИЯ
Рπ2
C2
ΔZ
А2
22
32
K2
12
B2
ФПГ
42
D2
Х
31
В1
Рx
С1
К1
ГПФ
21
11
41
А0
А1
Рπ1
D1
0
23.
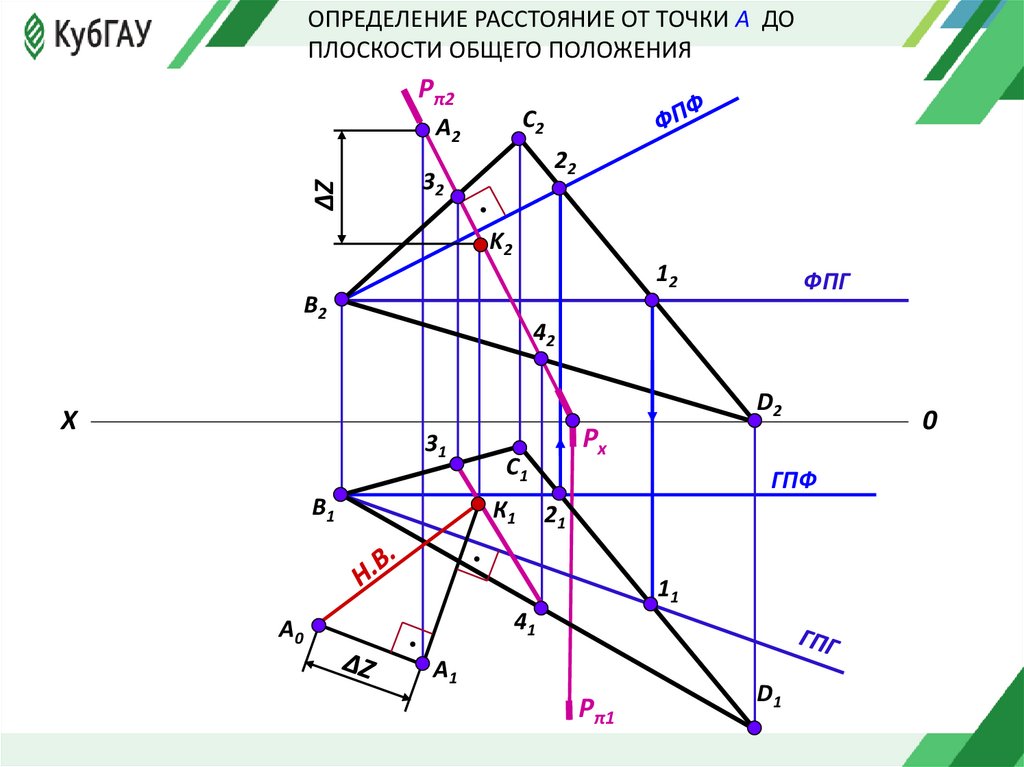
Если требуется определить расстояние от точки до плоскости общего положения,например, ∆ВСD.
Для решения задачи используем алгоритм:
1. Проводим в треугольнике ВСD горизонталь h1, h2 .
2. Проводим в треугольнике фронталь f1, f2.
3. Из точки А2 опускаем перпендикуляр к f2
4. Из точки А1 опускаем перпендикуляр к h1
5. Заключаем перпендикуляр, опущенный из точки А2 во фронтально-проецирующую
плоскость Рп2.
6. Находим точки пересечения следа Рп2 со сторонами треугольника 32 42.
Спроецируем линию пересечения на горизонтальную проекцию треугольника 3141.
7. На пересечении горизонтальной проекции линий пересечения плоскостей и
горизонтальной проекции перпендикуляра определяем точку встречи перпендикуляра с
плоскостью К1. Находим фронтальную проекцию точки встречи перпендикуляра с
плоскостью К2
8. Определяем натуральную величину перпендикуляра методом прямоугольного
треугольника. Для этого замеряем величину ∆z , строим на горизонтальной проекции
прямоугольный треугольник, у которого один катет является проекцией перпендикуляра
К1 , а второй – величиной ∆ z. Гипотенуза этого треугольника есть натуральная величина



















 Инженерная графика
Инженерная графика








