Умножение вектора на число

1. Умножение вектора на число.

2. Упростите выражение:

1 вариант.
2 вариант.
CA – OB – CD + AB =
BA + CD – OD – CA =
= CA + BO + DC + AB =
= BA + CD + DO + AC =
= DC + CA + AB + BO =
= BA + AC + CD + DO =
= DO.
= BO.

3.

Тема: Действия над векторами. Умножение вектора на число
Цели обучения:
9.1.4.2 знать и применять правила умножения вектора на
число;

4. Умножение вектора на число

Произведением вектора a на число t называется вектор,
длина которого равна | t | | a |, а направление остается
прежним, если t>0, и меняется на противоположное, если
t < 0. Произведением вектора на нуль считается нулевой
вектор.
Произведение вектора a на число t обозначается ta . По
определению, | ta | | t | | a | .
Произведение вектора a на число -1 называется
вектором, противоположным и обозначается
По
определению,
вектор a. имеет
направление,
противоположное вектору и | a | | a | .

5. Свойства

Для умножения вектора на число справедливы свойства,
аналогичные свойствам умножения чисел, а именно:
Свойство 1. (ts )a t ( sa ) (сочетательный закон).
Свойство 2. (t s )a ta sa (первый распределительный
закон).
Свойство 3. t (a b ) ta tb (второй распределительный
закон).

6.

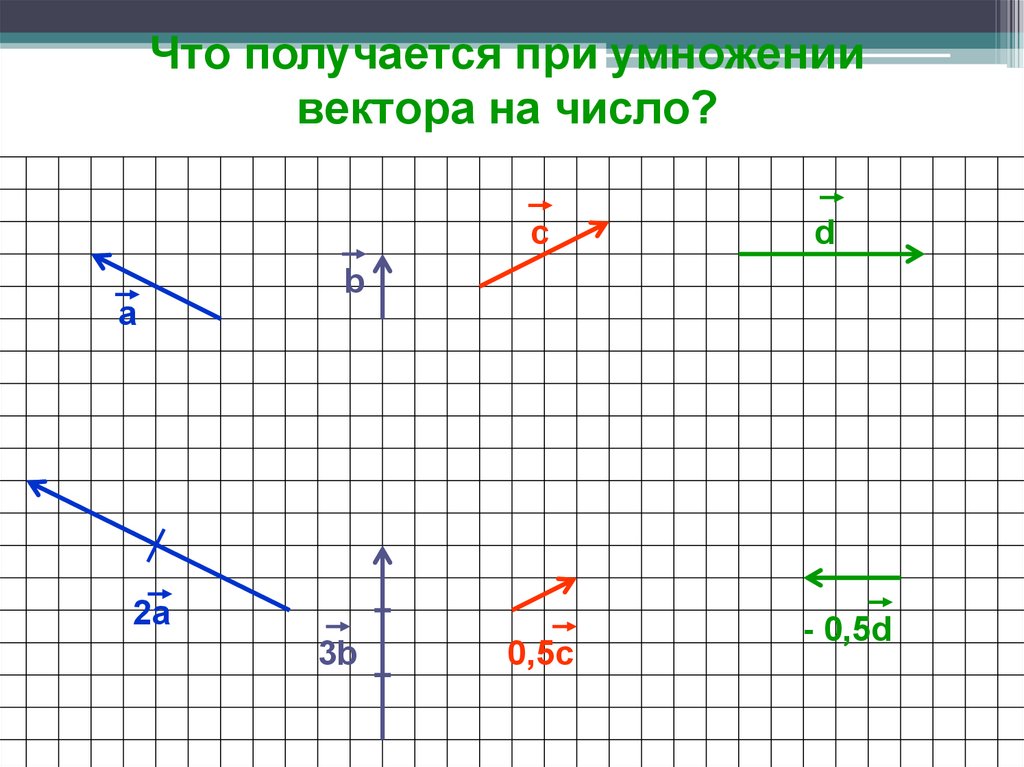
Что получается при умножении
вектора на число?
c
а
d
b
2а
3b
0,5с
- 0,5d

7. Упражнение 1

В треугольнике АВС укажите векторы:
а)
AC AB;
б)
AB AC;
в)
BA BC;
г)
BA CA.
BC.

8. Упражнение 2

В параллелограмме АВСD укажите векторы:
а)
AB AD;
б)
AD AB;
в)
CB AB;
г)
CB DA;
д)
CB AD.

9. Упражнение 3

Точки M и N - середины сторон соответственно
АВ и АС треугольника АВС. Выразите векторы:
а) BM ; б) NC ; в) MN ; г) BN ; д) CB через
векторы a AM , b AN .

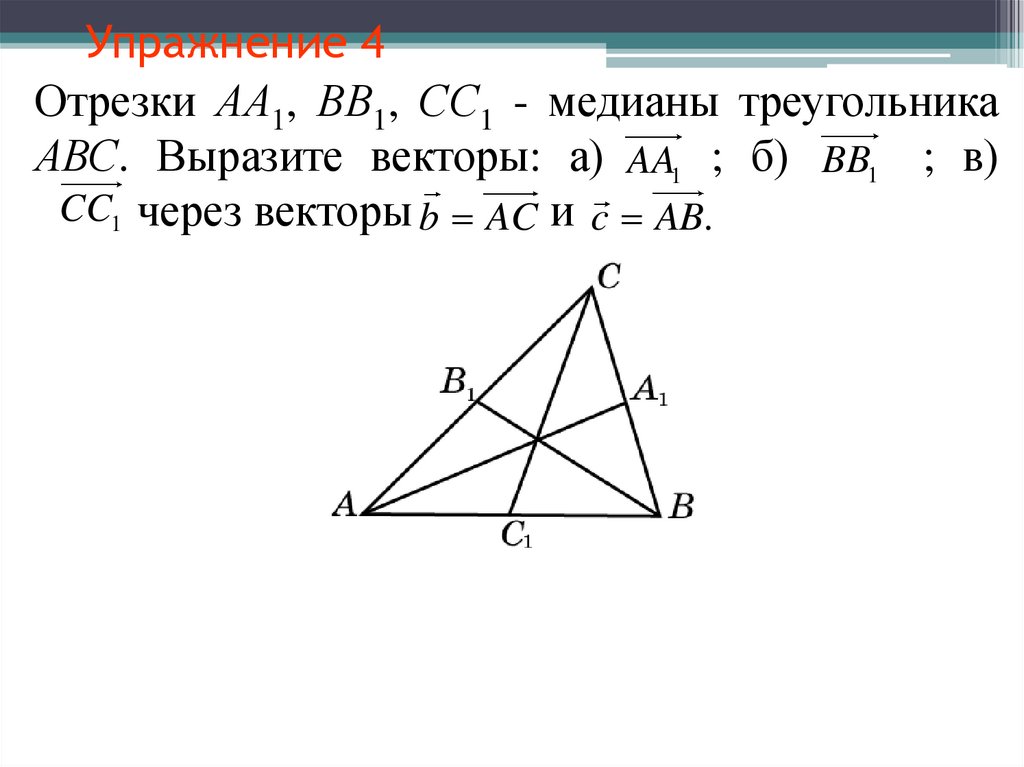
10. Упражнение 4

Отрезки АА1, ВВ1, СС1 - медианы треугольника
АВС. Выразите векторы: а) AA1 ; б) BB1 ; в)
CC1 через векторы b AC и c AB.

11. Упражнение 5

Упростите выражение:
а) ( AB AC ) ( BA CB);
б)
AB DB CA DA.

12. Упражнение 6

Сторона равностороннего треугольника АВС
равна а. Найдите: а)| BA BC |; б) | AB AC | .
Ответ: а) a;
б) a.

13. Упражнение 7

В треугольнике АВС АВ = 6, ВС = 8, B = 90°.
Найдите: а) | BA | | BC |; б) | BA BC | ; в) | AB | | BC | ;
г) | AB BC | .