Числовая окружность на координатной плоскости

1.

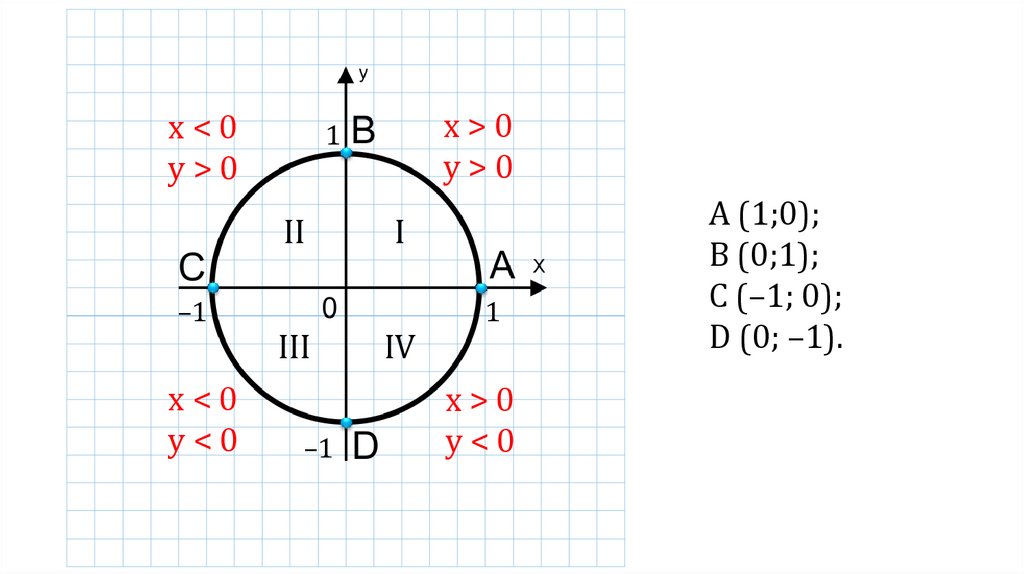
x<0
y>0
II
–1
x<0
y<0
x>0
y>0
1
III
–1
I
IV
1
x>0
y<0
А (1;0);
В (0;1);
С (–1; 0);
D (0; –1).

2.

E (x;y) – точка окружности;
уравнение окружности: х2 + у2 =R2;
–1≤ х ≤ 1;
–1≤ у ≤1;
0
0

3.

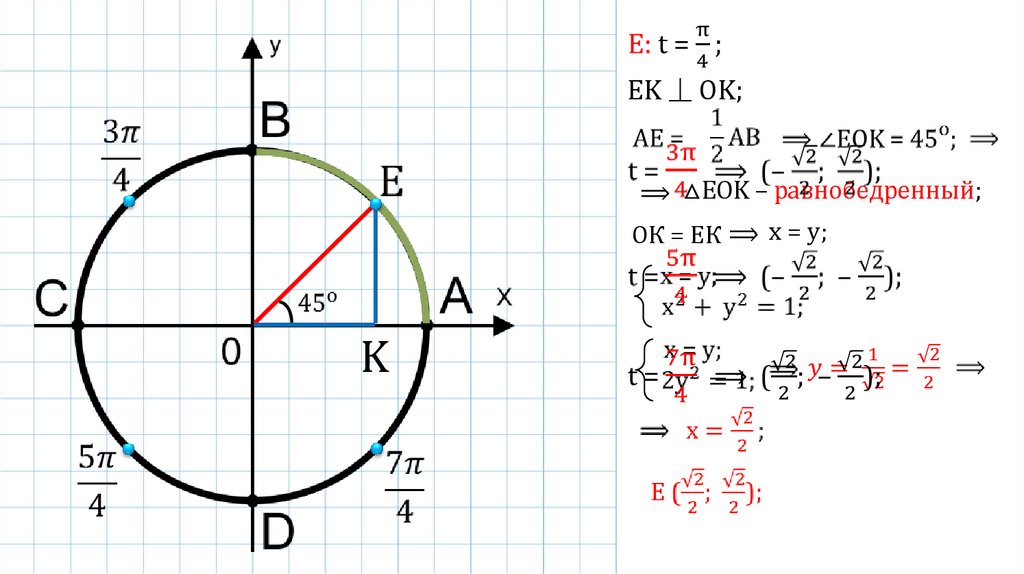
EK ⏊ OK;
△EOK – равнобедренный;
ОК = ЕК
K
x = y;

4.

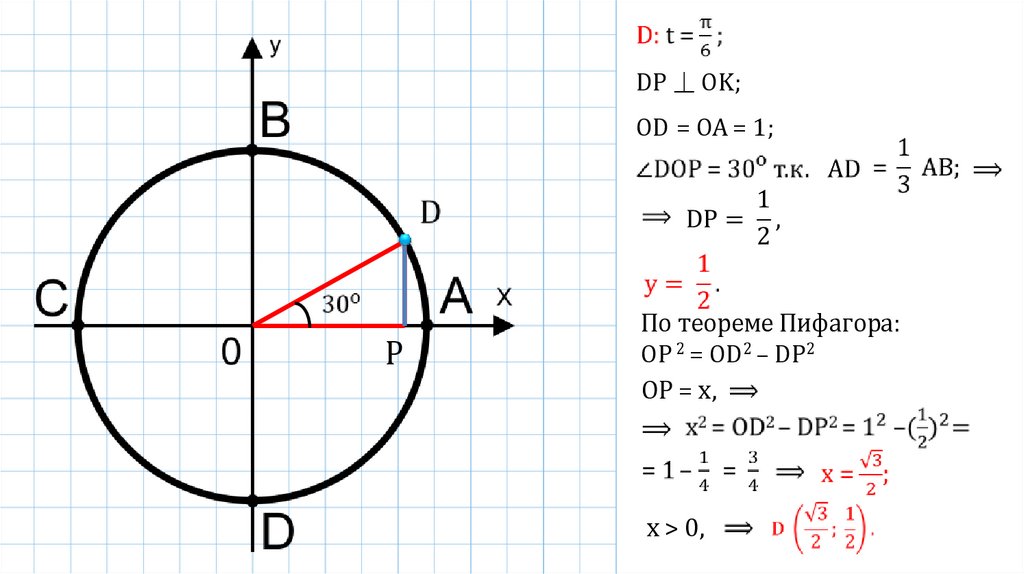
DP ⏊ OK;
ОD = OA = 1;
P
По теореме Пифагора:
ОР 2 = ОD2 – DР2
ОР = х,
x > 0,

5.

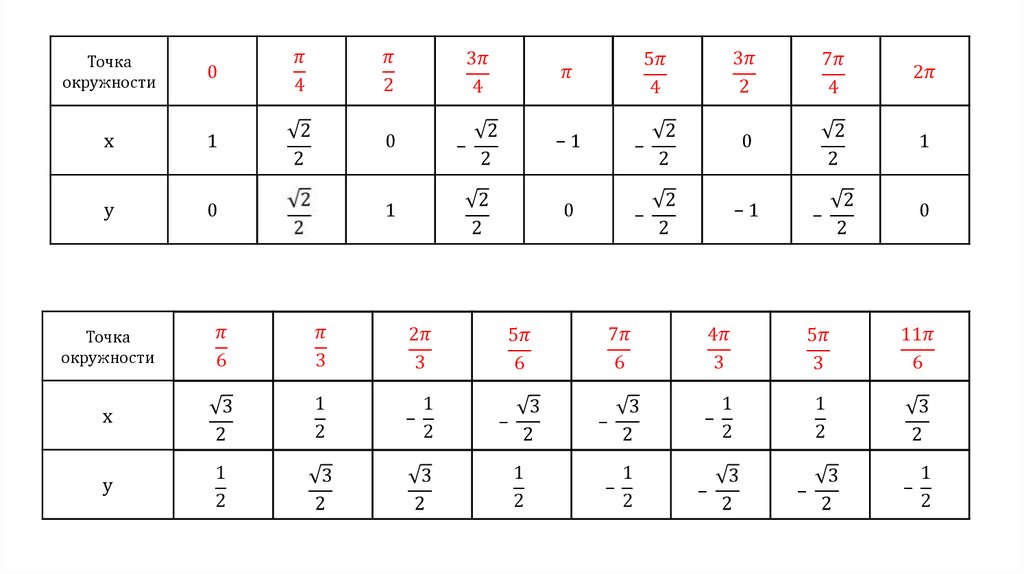
Точка
окружности
0
x
1
0
–1
0
1
y
0
1
0
–1
0
Точка
окружности
x
y

6.

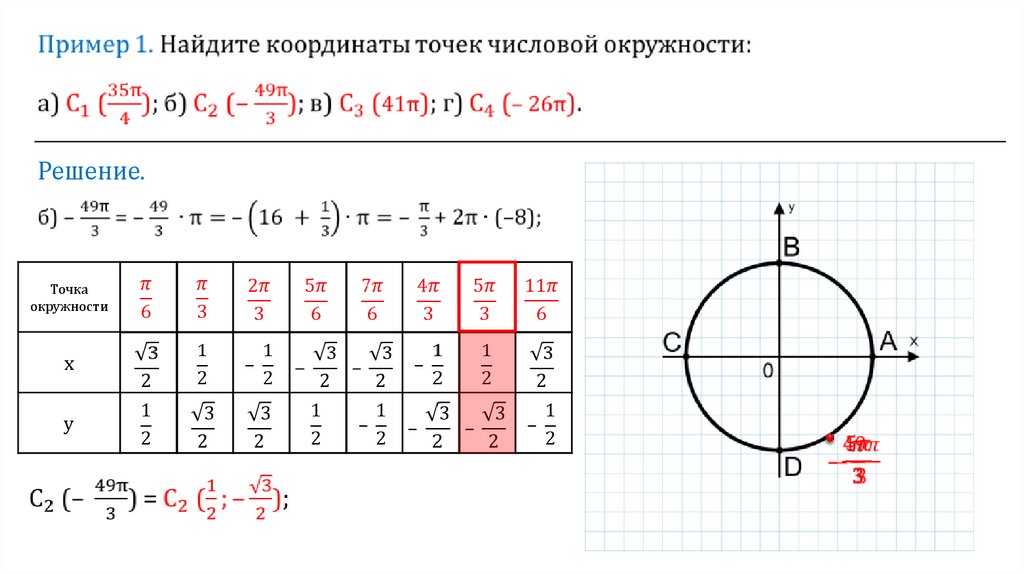
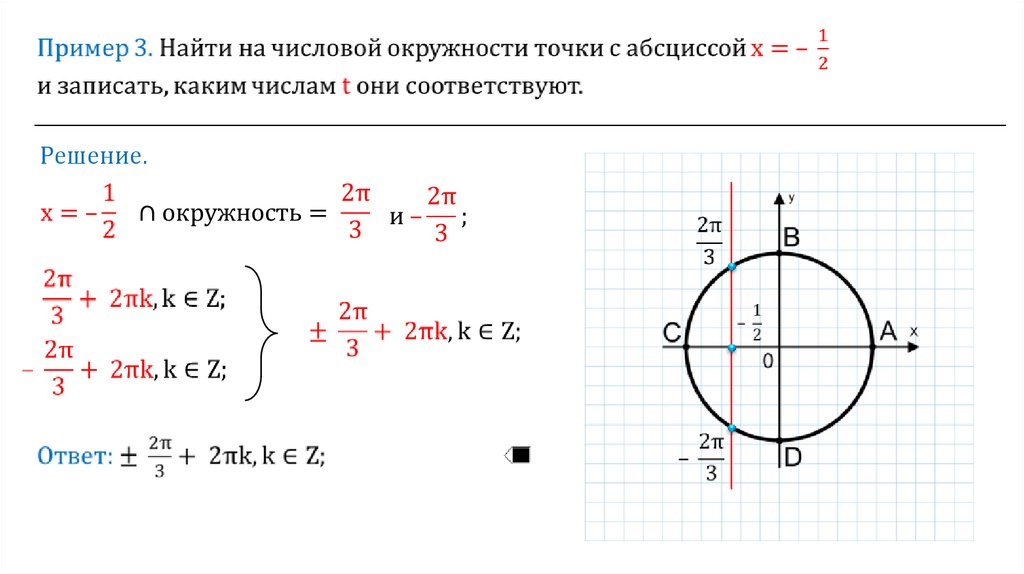
Решение.

7.

Если точка D числовой окружности
соответствуют числу t, то она
соответствует и любому числу вида t + 2πk,
где k ϵ Z.

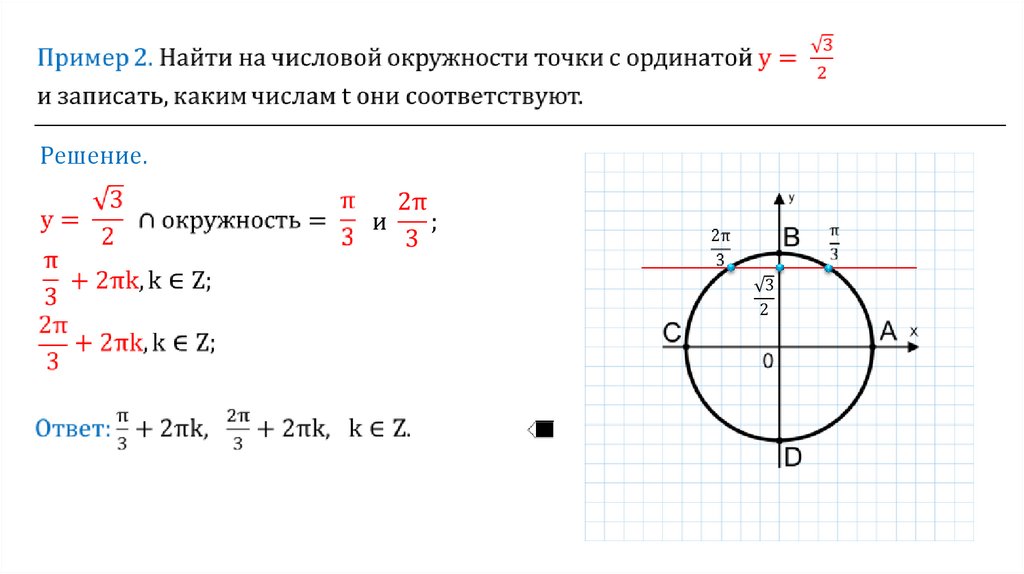
8.

Решение.
Точка
окружности
0
x
1
0
–1
0
1
y
0
1
0
–1
0

9.

Решение.
Точка
окружности
x
y

10.

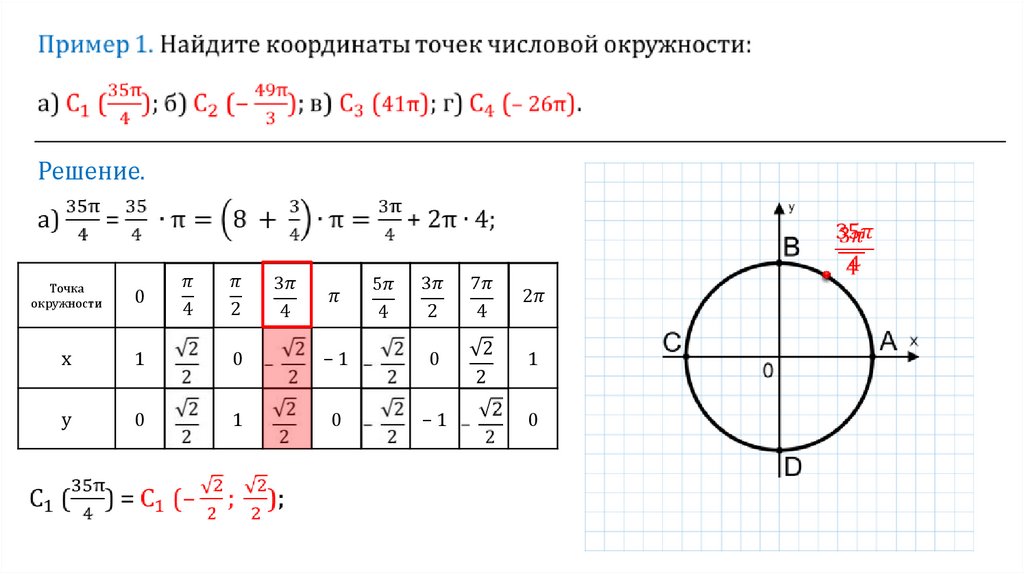
Решение.
в) 41π = 40π + π = π + 2π ∙ 20;
г) – 26π = 0 + 2π ∙ ( – 13);
С4( – 26π)= С4(1; 0).
0

11.

Решение.

12.

Решение.