Векторная алгебра. Скалярное произведение векторов

1.

2.

2. ВЕКТОРНАЯ АЛГЕБРА
2.1 Векторы, общие понятия
2.2 Скалярное произведение векторов
2.3 Векторное произведение векторов
2.4 Смешанное произведение векторов

3.

2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ОПР. Скалярным произведением двух векторов a и b
называется число (скалярная величина), равная
произведению модулей этих векторов на косинус угла
между ними:
a b a b cos
Обозначение:
a b или
a,b
Свойства скалярного произведения
1)
a b b a
2)
(a b ) c a c b c
3)
( a ) b (a b ) a ( b )

4.

2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства скалярного произведения (продолжение)
4) Связь скалярного произведения с проекцией одного вектора на
ось, задаваемую другим:
a b a b cos a ПРa b
a b a cos b ПРb a b
ПРa b
a b
ПРb a
b
5) Связь скалярного произведения с длиной вектора:
a a a a cos0 a
2
длина вектора равна квадратному
корню из скалярного квадрата:
a b
a
a a
2
2
a a2

5.

2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства скалярного произведения (продолжение)
6) Нахождение угла между векторами:
cos cos a , b
a b
cos
a b
m
а) если - острый угол, то
cos 0 a b 0
arccos m
б) если - тупой угол, то
cos 0
a b 0
arccos m

6.

2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства скалярного произведения (продолжение)
7) КРИТЕРИЙ ПЕРПЕНДИКУЛЯРНОСТИ ВЕКТОРОВ
a b a b 0
!

7.

2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление скалярного произведения векторов,
заданных координатами
i 1;0;0 , j 0;1;0 , k 0;0;1
" " i
j
k
По определению скалярного произведения:
i
1
0
0
i i i i cos 00 1
j
0
1
0
j j j j cos 00 1
k
0
0
1
k k k k cos 00 1
i j j i i j cos900 0
j k k j j k cos900 0
k i i k k i cos900 0

8.

2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление скалярного произведения векторов,
заданных координатами
Пусть заданы векторы:
a ax ; a y ; az ax i a y j az k
b bx ; by ; bz bx i by j bz k
Найдем их скалярное произведение (выведем формулу):
a b ax i a y j az k bx i by j bz k
axbx i 1 i axby i 0 j axbz i 0 k
a ybx j0 i a yby j1 j a ybz j0 k
azbx k 0 i azby k 0 j azbz k 1 k ax bx a y by az bz
a b ax bx ay by az bz

9.

2.2 СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
Даны векторы:
a 0;1; 3 , b 1;1;2
1) Найти их скалярное произведение.
2) Найти косинус угла между ними.
3) Найти проекцию вектора
a на вектор b .
1) a b 0 1 1 1 3 2 5
5
5
5
a b
2) cos
2
10 6
2 15
a b
02 12 3 12 12 22
a b
3) ПРb a
b
5
5
2
2
2
6
1 1 2

10.

2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ОПР. Векторным произведением вектора a на вектор b
называется вектор c , такой что:
1) (длина вектора)
c a b sin
2) (направление вектора)
c a; c b
3) (направление вектора)
a , b , c правая тройка
Обозначение:
a b или
a , b
Свойства векторного произведения
1)
a b b a
2)
(a b ) c a c b c
3)
( a ) b (a b ) a ( b )

11.

2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Свойства векторного произведения (продолжение)
4) КРИТЕРИЙ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ
a b a b 0
!!

12.

2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление векторного произведения векторов,
заданных координатами
i 1;0;0 , j 0;1;0 , k 0;0;1
По определению векторного произведения:
2
" " i
1
j
k
i
0
k
j
i i i i sin 00 0
i i 0
j
k
0
i
j j j j sin 00 0
j j 0
j
i
0
k k k k sin 00 0
k k 0
k
i j i j sin 900 1
i j k
j k j k sin 900 1
j k i k j i
k i k i sin 900 1
k i j
j i k
i k j

13.

2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление векторного произведения векторов,
заданных координатами
Пусть заданы векторы:
a ax ; a y ; az ax i a y j az k
b bx ; by ; bz bx i by j bz k
Найдем их векторное произведение (выведем формулу):
a b ax i a y j az k bx i by j bz k
axbx i 0 i axby i k j axbz i kj
a ybx j
ki a yby j0 j a ybz ji k
azbx k j i azby k
ij azbz k 0 k

14.

2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление векторного произведения векторов,
заданных координатами
Сгруппируем по векторам:
i a ybz azby j axbz azbx k axby a ybx
Получили разложение определителя по 1 строке:
i
j
k
ax
ay
az
bx
by
bz
i
j
k
a b ax
ay
az
bx
by
bz

15.

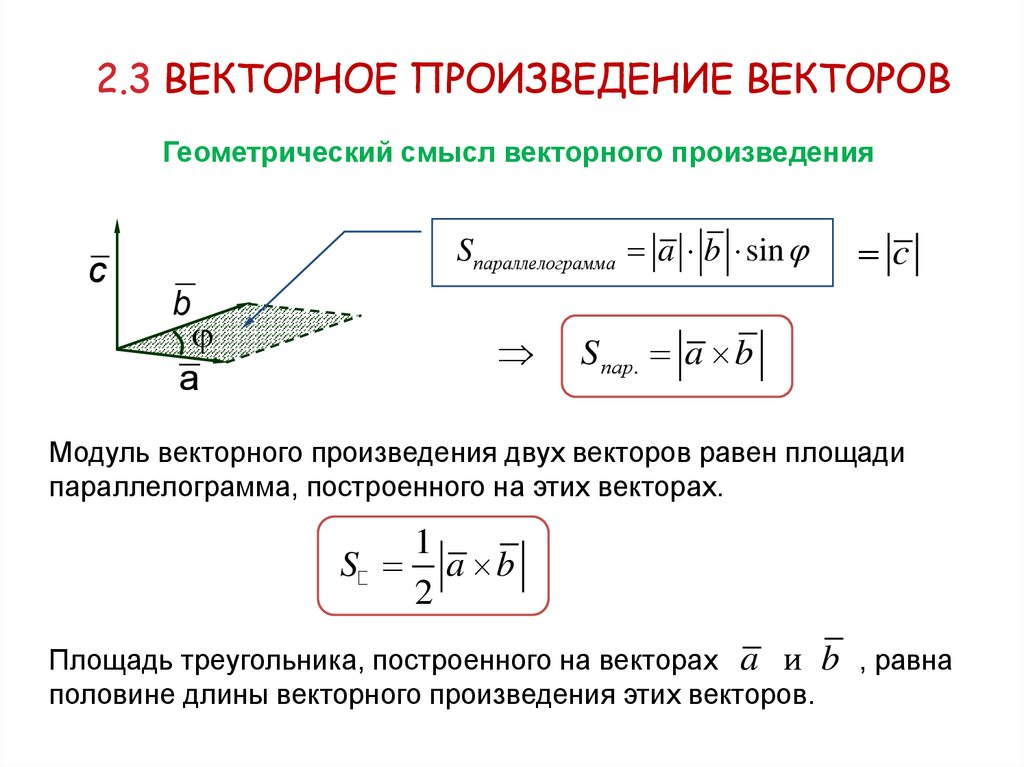
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Геометрический смысл векторного произведения
Sпараллелограмма a b sin
c
c
b
a
S пар. a b
Модуль векторного произведения двух векторов равен площади
параллелограмма, построенного на этих векторах.
1
S a b
2
Площадь треугольника, построенного на векторах a и b , равна
половине длины векторного произведения этих векторов.

16.

2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
1) Даны векторы:
a 3;0;2 , b 1;2; 1 .
Найти их векторное произведение.
i
j
a b 3 0
1
2
k
2 i 0 4 j 3 2 k 6 0
1
4 i j 6k 4; 1; 6

17.

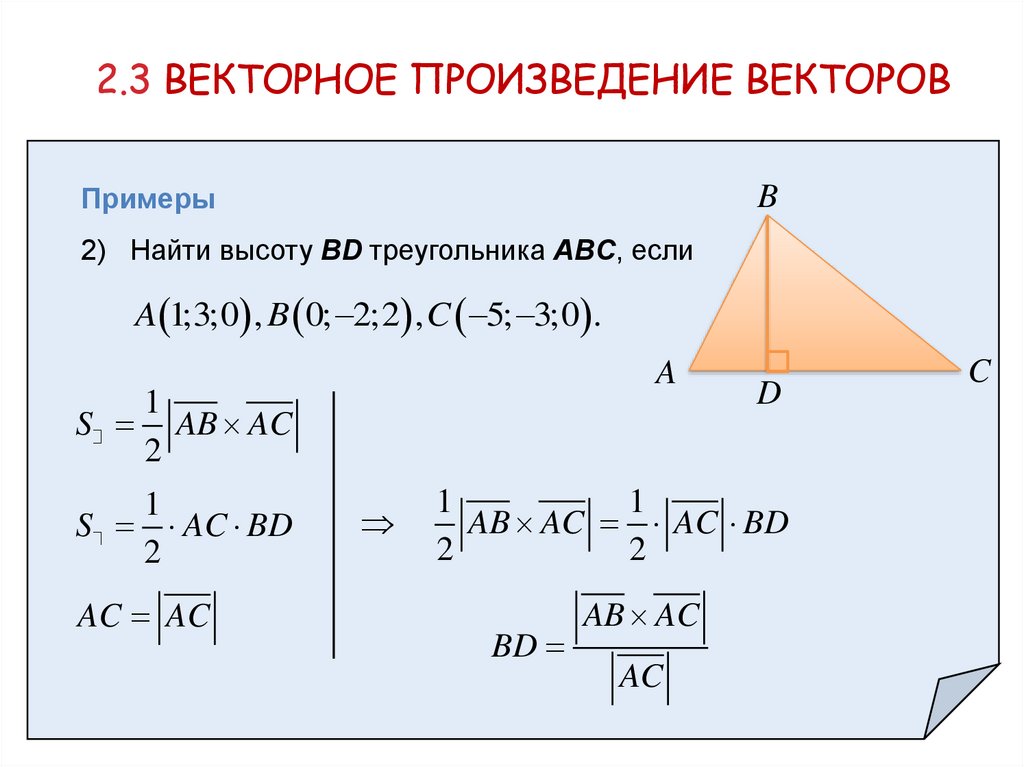
2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
B
2) Найти высоту BD треугольника ABC, если
A 1;3;0 , B 0; 2;2 , C 5; 3;0 .
A
1
S AB AC
2
1
S AC BD
2
AC AC
D
1
1
AB AC AC BD
2
2
BD
AB AC
AC
C

18.

2.3 ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Примеры
AB AC
BD
AC
A 1;3;0 , B 0; 2;2 , C 5; 3;0
AB 0 1; 2 3;2 0 1; 5;2
AC 5 1; 3 3;0 0 6; 6;0
i
j
k
AB AC 1 5 2 i 0 12 j 0 12 k 6 30
6 6
12 i 12 j 24k 12; 12; 24
0
AB AC 122 12 24 12 6
2
AC
6 6
2
2
02 6 2
2
12 6
BD
2 3
6 2

19.

2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
ОПР. Cмешанным произведением трех векторов
называется число (скалярная величина): a b c
Обозначение:
a b c,
или
a, b, c ,
или abc
Свойства смешанного произведения
1)
2)
3)
a b c a b c
a a bc a bc a bc
1
2
1
2
c
b
Закон круговой переместительности:
abc bca cab bac cba acb
a

20.

2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
3) Тройка векторов определяет знак смешанного произведения:
abc 0
a, b, c правая тройка,
abc 0
a, b, c левая тройка.
4) КРИТЕРИЙ КОМПЛАНАРНОСТИ ВЕКТОРОВ
!!!
a, b,c - компланарны abc 0
В частности, смешанное произведение равно нулю, если в нем
два множителя одинаковы:
aac 0

21.

2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление смешанного произведения векторов,
заданных координатами
Пусть заданы векторы:
a ax ; a y ; az ax i a y j az k
b bx ; by ; bz bx i by j bz k
c cx ; c y ; cz cx i c y j cz k
Найдем их смешанное произведение (выведем формулу):
abc a b c
a b i a ybz azby j axbz azbx k axby a ybx
a b a b ; a b a b ; a b
y z
z y
x z
z x
x y
a ybx

22.

2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Вычисление смешанного произведения векторов,
заданных координатами
Используем формулу для нахождения скалярного произведения
векторов, заданных координатами:
abc a b c cx a ybz azby c y axbz azbx cz axby a ybx
Получили разложение определителя по 1 строке:
cx
cy
cz
ax
ay
az
bx
by
bz
Поменяем два раза
местами строки: 1 и 2,
2и3
ax
ay
az
abc bx
by
bz
cx
cy
cz
ax
ay
az
bx
by
bz
cx
cy
cz

23.

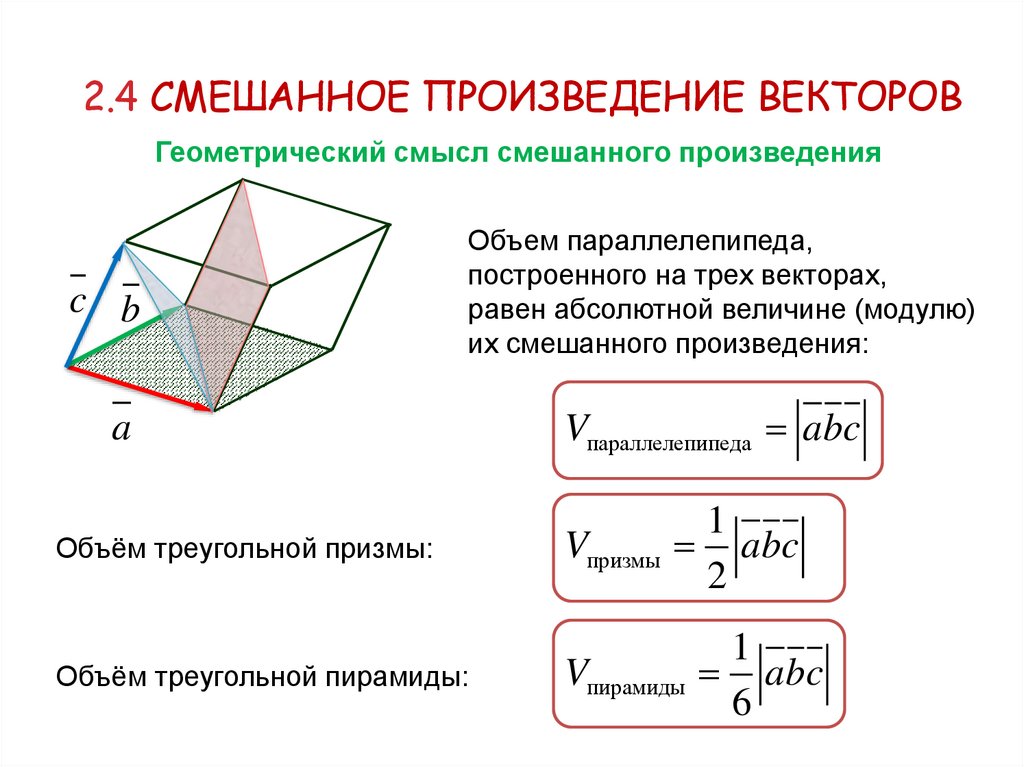
2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Геометрический смысл смешанного произведения
c b
Объем параллелепипеда,
построенного на трех векторах,
равен абсолютной величине (модулю)
их смешанного произведения:
a
Объём треугольной призмы:
Объём треугольной пирамиды:
Vпараллелепипеда abc
Vпризмы
1
abc
2
Vпирамиды
1
abc
6

24.

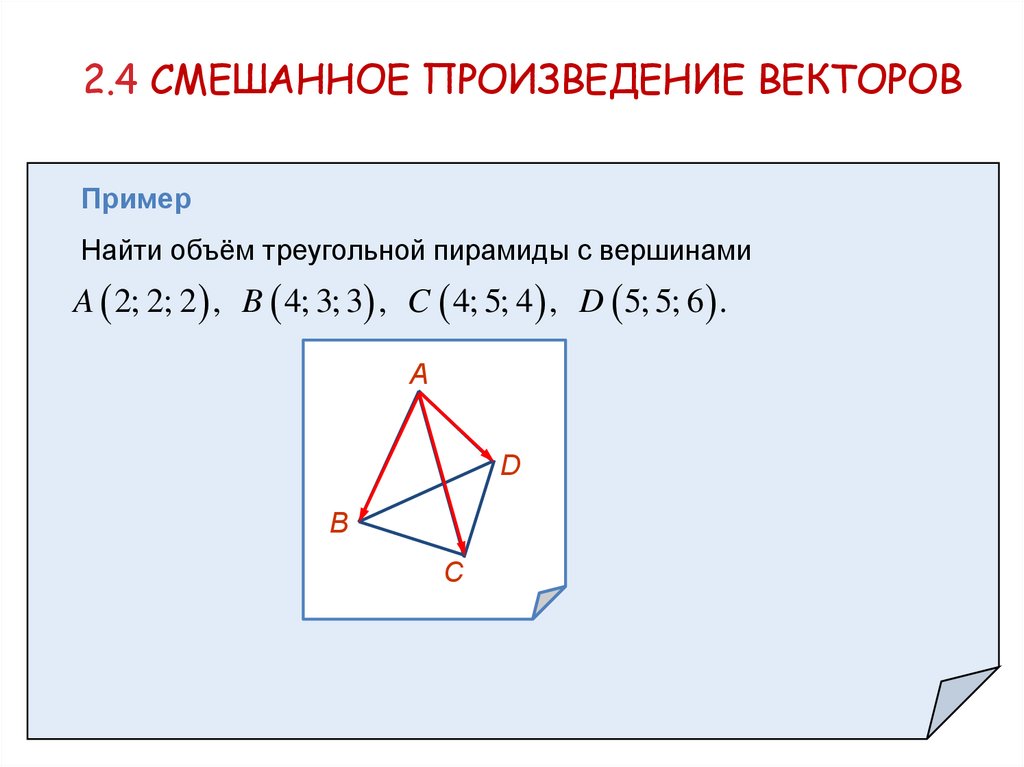
2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Пример
Найти объём треугольной пирамиды с вершинами
A 2; 2; 2 , B 4; 3; 3 , C 4; 5; 4 , D 5; 5; 6 .
А
D
В
С

25.

2.4 СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Пример
Vпирамиды
A 2; 2; 2 , B 4; 3; 3 , C 4; 5; 4 , D 5; 5; 6 .
1
AB, AC , AD
6
AB 4 2;3 2;3 2 2;1;1
AC 4 2;5 2;4 2 2;3;2
AD 5 2;5 2;6 2 3;3;4
AB, AC , AD
2 1 1
2 3 2 2 3 4 1 2 3 2 3 1
3 3 4 1 3 3 1 2 4 2 3 2
24 6 6 9 8 12 7
Vпирамиды
1
7
1
7 1
6
6
6

26.

Лекция выложена впервые.
Если Вы заметили ошибку, то сообщите мне на эл. почту.