Произведение векторов

1.

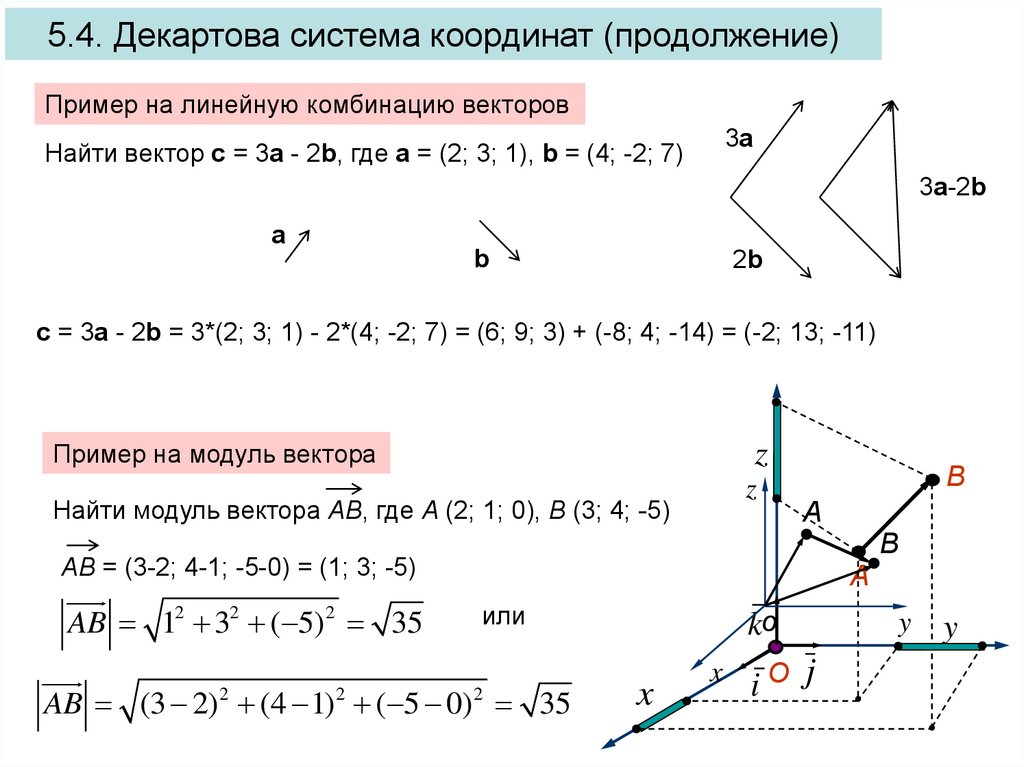
5.4. Декартова система координат (продолжение)
Пример на линейную комбинацию векторов
3a
Найти вектор c = 3a - 2b, где a = (2; 3; 1), b = (4; -2; 7)
3a-2b
a
b
2b
c = 3a - 2b = 3*(2; 3; 1) - 2*(4; -2; 7) = (6; 9; 3) + (-8; 4; -14) = (-2; 13; -11)
Пример на модуль вектора
z
z
Найти модуль вектора AB, где A (2; 1; 0), B (3; 4; -5)
В
A
B
AB = (3-2; 4-1; -5-0) = (1; 3; -5)
AB 12 32 ( 5)2 35
А
или
AB (3 2) (4 1) ( 5 0) 35
2
2
2
ko
x
x
iО j
y
y

2.

Пример на направляющие косинусы
Модуль вектора a равен 5. С осями координат Ox, Oy он образует углы
60 и 90 градусов соответственно. Найти его координаты.
cos2 cos2 cos2 1
2
1
2 1 2
2
a 5, 60 , 45 ,cos ,cos
,
cos 1
2
2 2 2
1 1 1
1
2
z
cos 1 cos
4 2 4
2
z
2
0
0
1
ax a cos 5 2,5;
2
2
a y a cos 5
2,5 2;
2
1
az a cos 5 2,5
2
М
x
x
О
y
y

3.

Пример на деление отрезков
Найти длину медианы CD треугольника, заданного вершинами
A(-1;2;5), B(3;0;1), C(2;3;4).
x A x B 1 3
xD
1
2
2
y yB 2 0
yD A
1
2
2
z A zB 5 1
zD
3
2
2
D(1;1;3)
С
CD (1 2;1 3; 3 4) ( 1; 2; 1)
CD 1 4 1 6
В
А
D

4. 6.1. Скалярное произведение векторов

Скалярным произведением двух векторов называется число, равное
произведению модулей векторов на косинус угла между ними.
a b a b cos ab
a
b
Скалярное произведение векторов в координатной форме
a xa , ya , za ,
b xb , yb , zb
Докажем для двумерного случая
a b xa xb ya yb za zb
cos cos cos sin sin
cos cos cos cos 90o cos 90o
ya
xa xb ya yb
cos ab cos
a b a b
yb
xa xb ya yb
a b cos ab a b
a b a b
xa
xb

5.

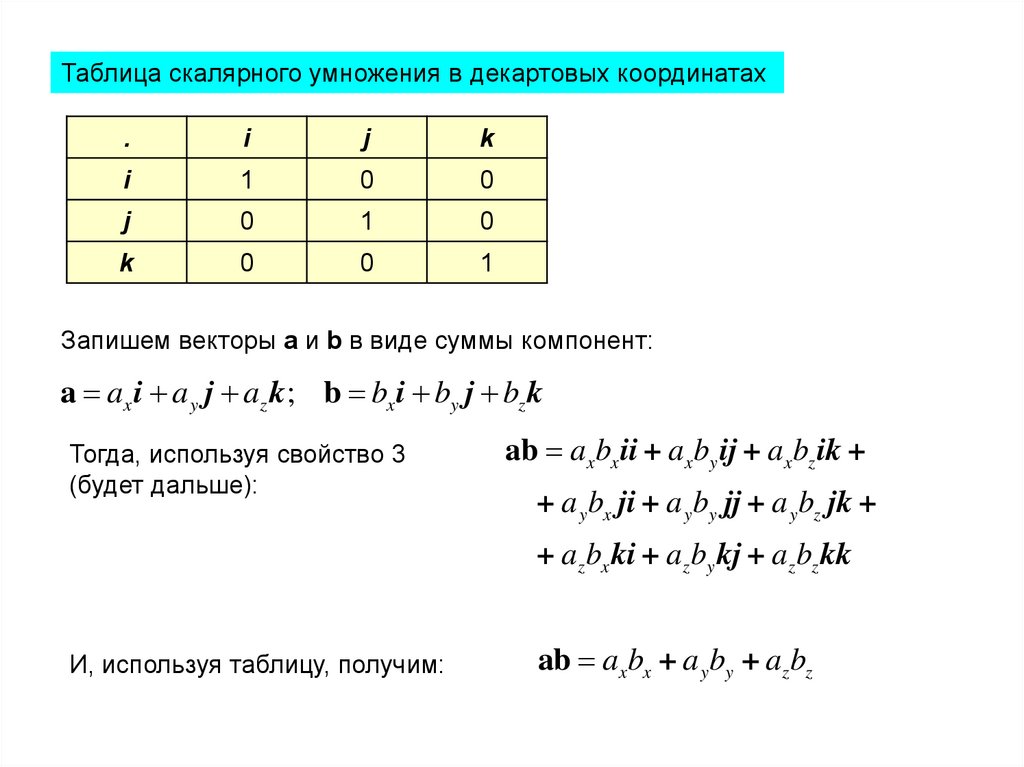
Таблица скалярного умножения в декартовых координатах
.
i
j
k
i
1
0
0
j
0
1
0
k
0
0
1
Запишем векторы a и b в виде суммы компонент:
a ax i a y j az k ; b bx i by j bz k
Тогда, используя свойство 3
(будет дальше):
ab axbx ii + axby ij + axbz ik +
+ a y bx ji + a y by jj + a ybz jk +
+ az bx ki + az by kj + az bz kk
И, используя таблицу, получим:
ab axbx + a yby + az bz

6.

Свойства скалярного произведения.
1. a b b a
2. ( a) b (a b)
a b
5. cos
a b
Из определения скалярного произведения
3. a (b c) a b a c
4. a b a прa b b прb a
Из свойств скалярной проекции
2
6. a a a a
2
7. a b a b 0

7.

Некоторые из свойств в декартовых координатах (пригодится в задачках)
Условие ортогональности (из свойства 7):
axbx a yby az bz 0
Или, в двумерном случае:
axbx a yby 0
Модуль вектора (из свойства 6):
a a ax2 a y2 az2
2
2
a ax2 a y2 az2
Угол между двумя векторами (из свойства 5):
axbx a y by az bz
ab
cos
ab
ax2 a y2 az2 bx2 by2 bz2

8.

Проекция вектора на вектор (из свойства 4):
ab ab axbx a y by az bz
ï ðba a cos a
ab
b
bx2 by2 bz2
Где используется скалярное произведение:
(1) нахождение модуля вектора или отрезка;
(2) нахождение угла между векторами;
(3) использование условия ортогональности двух векторов;
(4) нахождение проекции вектора на вектор;
(5) различные задачи физического содержания.

9.

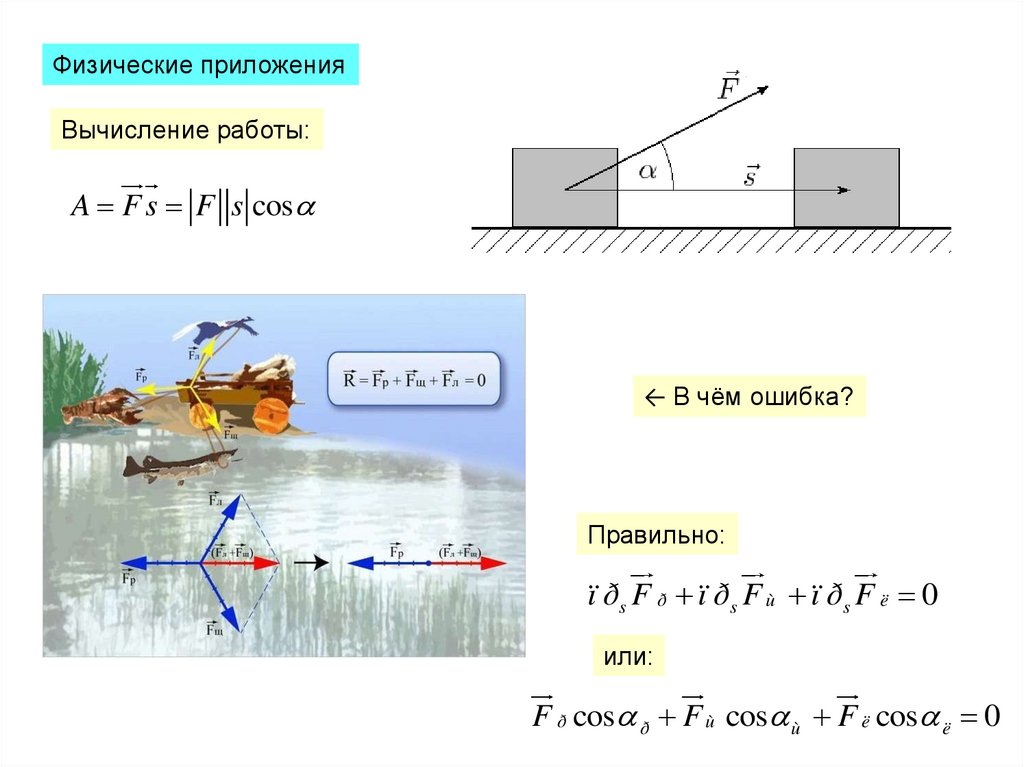
Физические приложения
Вычисление работы:
A F s F s cos
← В чём ошибка?
Правильно:
ï ðs F ð ï ðs F ù ï ðs F ë 0
или:
F ð cos ð F ù cos ù F ë cos ë 0

10.

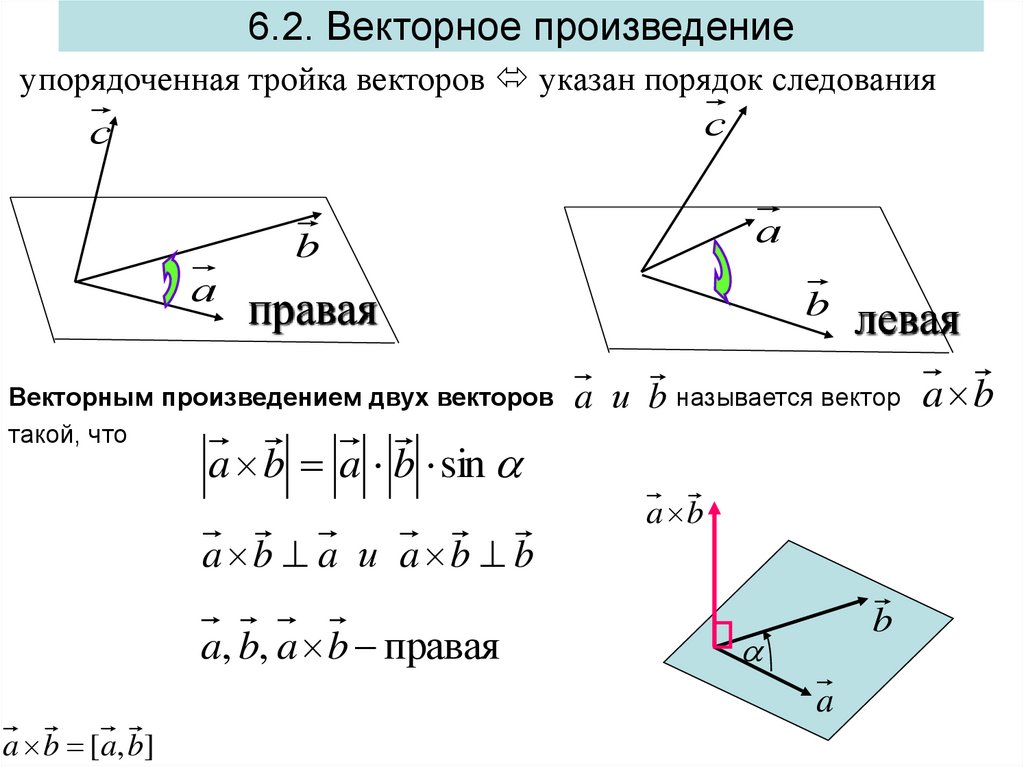
6.2. Векторное произведение
упорядоченная тройка векторов указан порядок следования
с
с
а
b
а
правая
Векторным произведением двух векторов
такой, что
b
левая
a и b называется вектор a b
a b a b sin
a b a и a b b
a, b, a b правая
a b
b
a
a b [ a, b]

11.

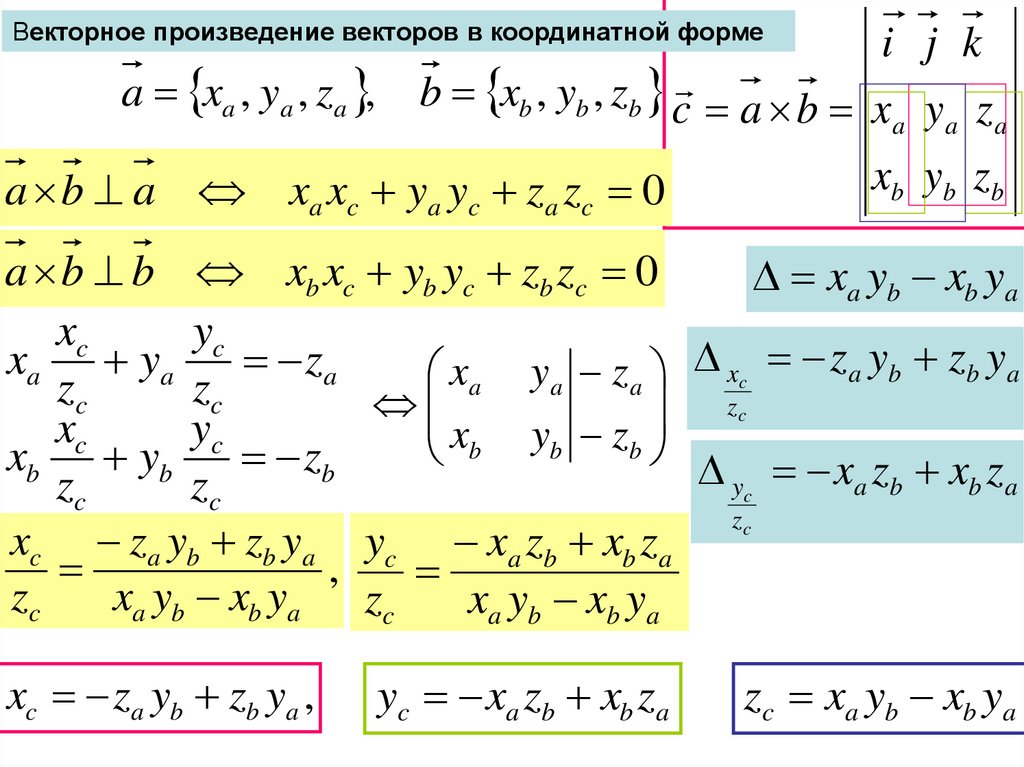
Векторное произведение векторов в координатной форме
a xa , ya , za ,
i j k
b xb , yb , zb c a b x y z
a
a a
a b a xa xc ya yc za zc 0
xb yb zb
a b b xb xc yb yc zb zc 0
xa yb xb ya
xc
yc
xc z a yb z b y a
xa ya
za
x
y
z
a
a
a
zc
zc
zc
xc
yc
x
y
z
b
b
b
xb yb
zb
yc xa zb xb za
zc
zc
zc
xc za yb zb ya yc xa zb xb za
,
zc
xa yb xb ya zc
xa yb xb ya
xc za yb zb ya ,
yc xa zb xb za
zc xa yb xb ya

12.

Получим то же самое, пользуясь таблицей векторного умножения:
x
i
j
k
i
0
k
-j
j
-k
0
i
k
j
-i
0
Запишем векторы a и b в виде суммы компонент:
a ax i a y j az k ; b bx i by j bz k
Тогда, используя свойство 3
(будет дальше):
a b ax i a y j az k bx i by j bz k
ax bx i i + ax by i j + ax bz i k +
+ a y bx j i + a y by j j + a y bz j k +
И, используя таблицу,
получим:
+ az bx k i + az by k j + az bz k k
a b a y bz az by i - ax bz az bx j + ax by a y bx k

13.

Что, в свою очередь, сворачивается в сумму миноров:
a b
ay
az
by
bz
i-
ax
az
bx
bz
j+
ax
ay
bx
by
k
которая является разложением определителя 3-го порядка, т.е.
i
j
k
a b ax
ay
az
bx
by
bz

14.

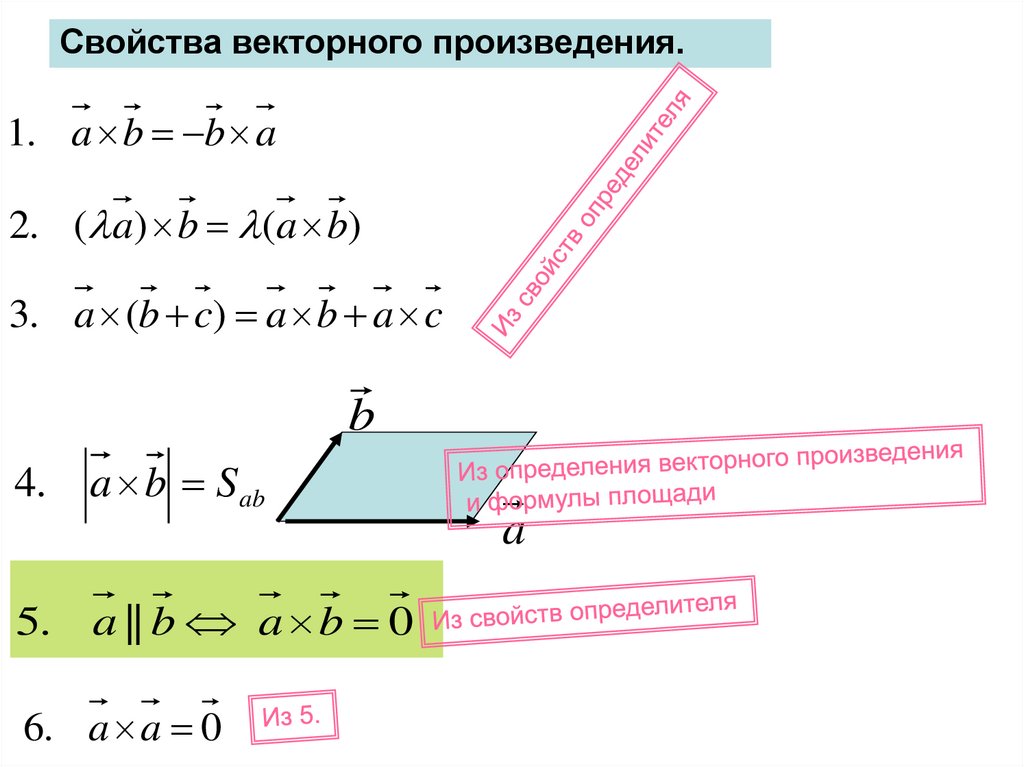
Свойства векторного произведения.
1. a b b a
2. ( a) b (a b)
3. a (b c) a b a c
b
4.
a b Sab
5. a || b a b 0
6. a a 0
a

15.

Некоторые из свойств в декартовых координатах (пригодится в задачках)
Условие колинеарности двух векторов (из свойства 5):
a || b a b 0
Это означает, что все координаты равны нулю:
a y bz az by 0; ax bz az bx 0; ax by a y bx 0
a y bz az by ; ax bz az bx ; ax by a y bx
ay
a
z;
by bz
ax az
;
bx bz
ax a y
bx by
или
ax a y az
bx by bz
т.е. координаты колинеарных векторов пропорциональны.

16.

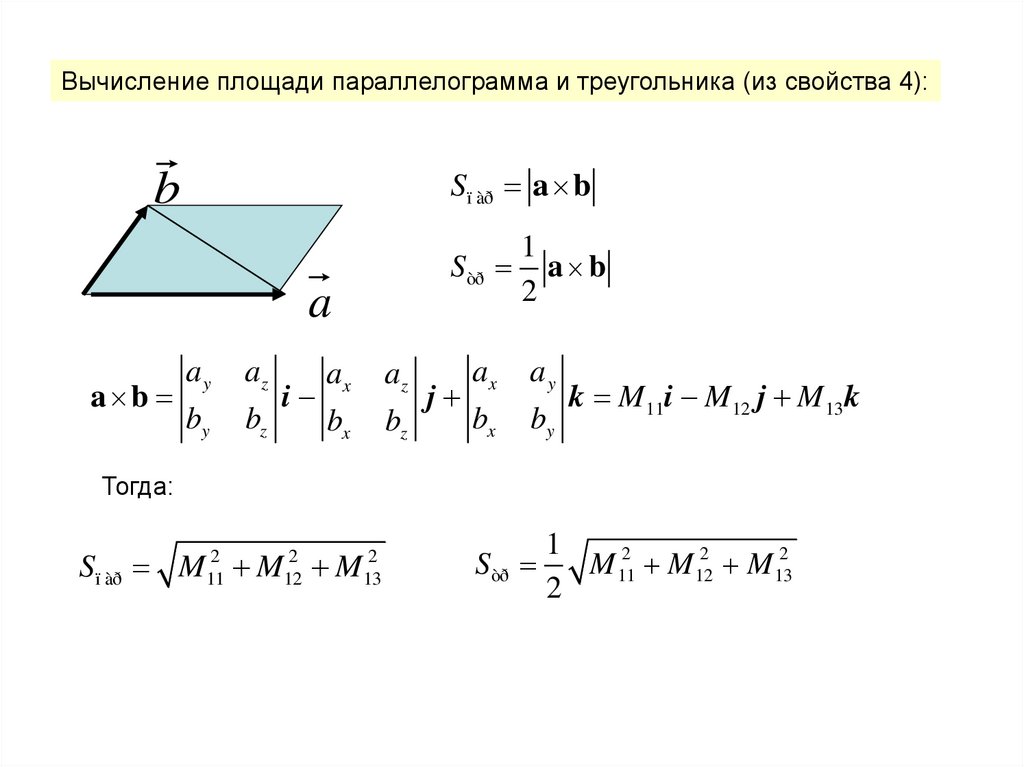
Вычисление площади параллелограмма и треугольника (из свойства 4):
Sï àð a b
b
S òð
a
a b
ay
az
by
bz
i
ax
az
bx
bz
j
1
a b
2
ax
ay
bx
by
k M 11i M 12 j M 13 k
Тогда:
Sï àð M M M
2
11
2
12
2
13
S òð
1
M 112 M 122 M 132
2

17.

Где используется векторное произведение:
(1) вычисление площади параллелограмма, треугольника и фигур,
которые можно на них разбить;
(2) нахождение модуля вектора или длины отрезка;
(3) различные геометрические задачи, связанные с площадью,
например, вычисление высоты параллелограмма или треугольника;
(4) использование условия колинеарности двух векторов;
(5) различные задачи физического содержания, связанные с моментом
силы и т.п.

18.

Пример на нахождение площади треугольника
Вычислить площадь треугольника, построенного на векторах p и q:
p = 2a+b, q = 3a - 2b, |a| = 2, |b| = 3, угол (a, b) = π/3.
1
p q
2
p q (2a b) (3a 2b) 6a a 4a b 3b a 2b b
S
4a b 3a b 7a b
p q 7 a b 7 a b sin / 3 7 2 3
S
1
p q 10,5 3
2
3
21 3
2

19.

Пример на нахождение площади треугольника в декартовых координатах
Вычислить площадь треугольника с вершинами в точках
A(1; 2; 1), B(-3; 2; 5), C(2; 0; 4).
S
1
AB AC
2
AB ( 3 1)i (2 2) j (5 1)k = 4i 4k
AC (2 1)i (0 2) j (4 1)k i 2 j 3k
i
AB AC 4
1
j
k
0
4 4 1
2 3
i
1
j
k
0
1
2 3
0
1
2 3
i
1 1
1
3
4(2i 4 j 2k ) 8(i 2 j k )
AB AC 8 1 4 1 8 6
1
S 8 6 4 6
2
j
1
0
1
2
k

20.

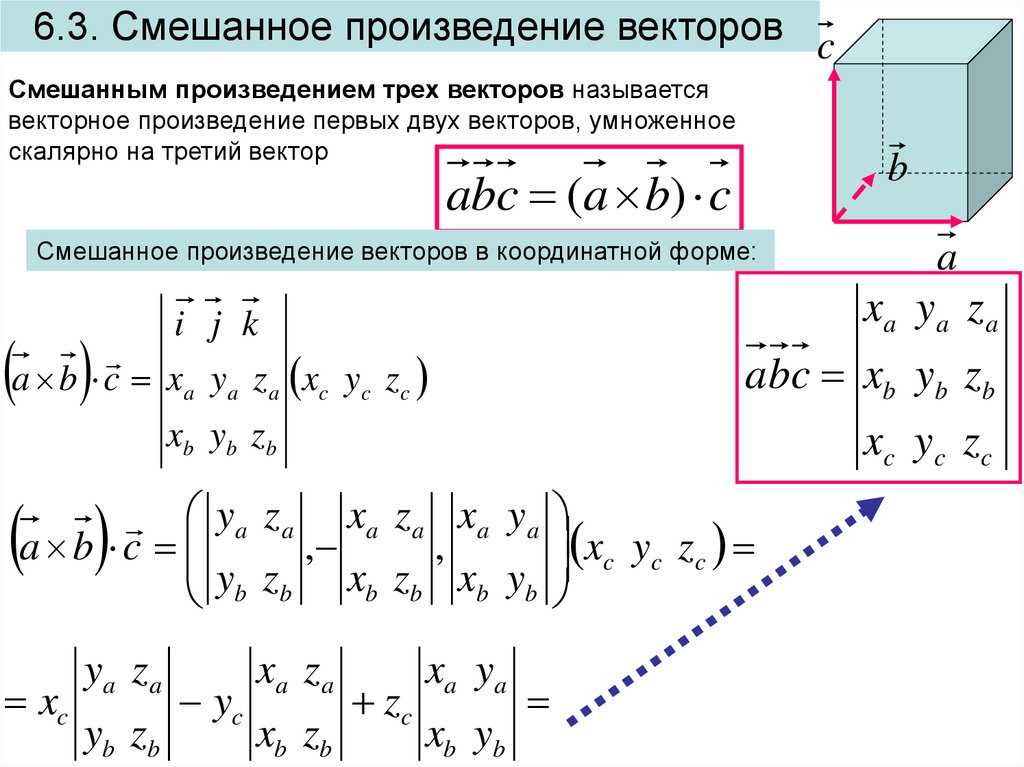
6.3. Смешанное произведение векторов c
Смешанным произведением трех векторов называется
векторное произведение первых двух векторов, умноженное
скалярно на третий вектор
b
abc (a b) c
Смешанное произведение векторов в координатной форме:
xa y a z a
i j k
a b c x a y a z a xc y c z c
abc xb yb zb
xb yb zb
xc yc zc
y a z a xa z a x a y a
xc yc zc
a b c
,
,
y
z
x
z
x
y
b b
b
b
b b
xc
ya z a
yb zb
yc
xa za
xb zb
a
zc
xa ya
xb yb

21.

Свойства смешанного произведения.
1. abc cab bca bac acb cba
2. abc abc a bc ab c
3.
abc Vпараллелепипеда
abc 0 левая тройка
abc 0 правая тройка
4. abc 0 a, b, c компланарны

22.

Подробнее…
Вычисление объёма параллелепипеда, призмы и пирамиды (свойство 3):
Даны некомпланарные векторы b, c, a.
Построим на них параллелепипед:
Из свойств векторного произведения:
b c Sbc
Высота параллелепипеда:
h a cos
Vï àð Sbc h b c a cos
b c a bca
С учётом возможной ситуации cosα < 0:
Vï àð bca

23.

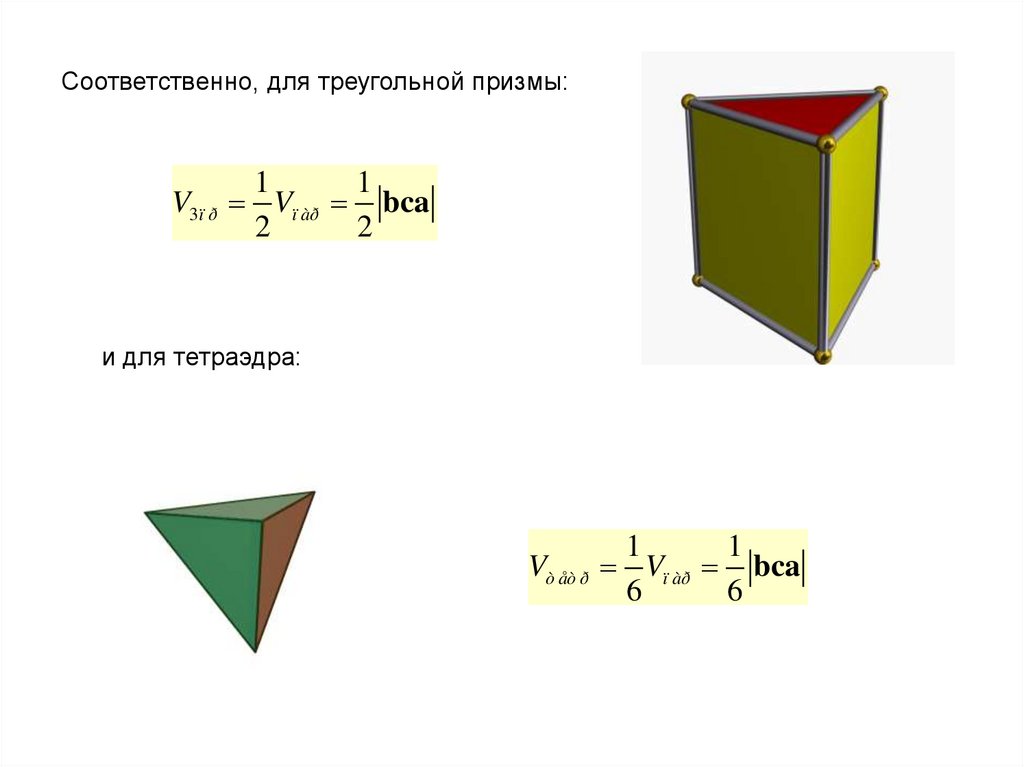
Соответственно, для треугольной призмы:
V3ï ð
1
1
Vï àð bca
2
2
и для тетраэдра:
Vò åò ð
1
1
Vï àð bca
6
6

24.

Условие компланарности трёх векторов (свойство 4):
Пусть даны:
a ax , a y , az , b bx , by , bz , c cx , c y , cz
a, b, c компланарны, если abc = 0. В самом деле:
ax
ay
az
abc bx
by
bz
cx
cy
cz
ax
ay
az
bx
by
bz 0
cx
cy
cz
С другой стороны,
a, b, c - компланарны c = xa + yb
Кроме того, это ясно из свойства 3.
Для компланарных векторов:
Vï àð 0 bca bca

25.

Где используется смешанное произведение:
(1) вычисление объёмов геометрических тел, ограниченных плоскими
гранями;
(2) решение геометрических задач, связанных с объёмом геометрических
тел, например, нахождение высоты, площади основания, углов между
рёбрами;
(3) использование условия компланарности, или линейной зависимости,
трёх векторов;
(4) решение различных физических задач.

26.

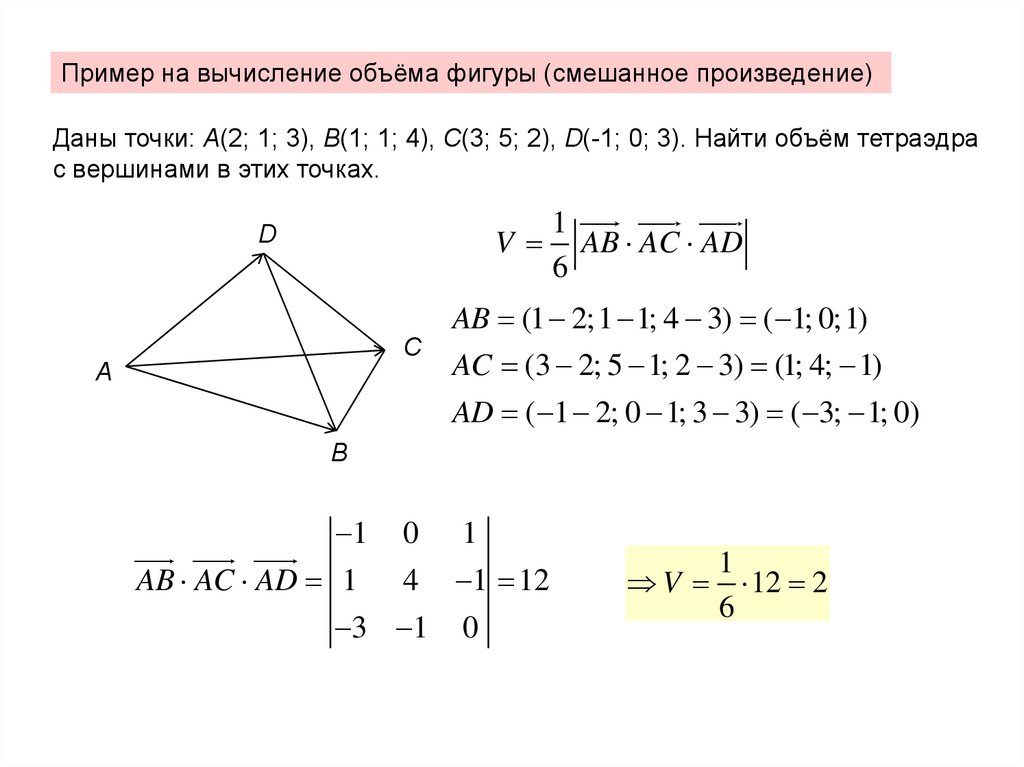
Пример на вычисление объёма фигуры (смешанное произведение)
Даны точки: A(2; 1; 3), B(1; 1; 4), C(3; 5; 2), D(-1; 0; 3). Найти объём тетраэдра
с вершинами в этих точках.
V
D
1
AB AC AD
6
AB (1 2;1 1; 4 3) ( 1; 0;1)
C
A
AC (3 2; 5 1; 2 3) (1; 4; 1)
AD ( 1 2; 0 1; 3 3) ( 3; 1; 0)
B
1
AB AC AD 1
0
1
4
1 12
3 1
0
1
V 12 2
6

27.

Задача на разложение вектора по базису
Даны три вектора a = (2, -1), b = (1, 2), c = (4, 3). Найти разложение вектора
m = a + b + c по векторам b и c.
Решение:
Пусть m = xb + yc.
Тогда m = a + b + c = xb + yc, или для координат:
(2+1+4, -1+2+3) = (x*1+y*4, x*2+y*3), откуда после упрощения:
(7, 4) = (x+4y, 2x+3y)
Получаем систему уравнений на x и y:
x 4 y 7
2 x 3 y 4
=> x = -1, y = 2
=> m = -b + 2c

28.

Пример на вычисление скалярного произведения
Дано: |a| = 3, |b| = 4, <(a, b) = 2π/3. Вычислить:
(а) a2;
(б) (3a - 2b)(a + 2b).
Решение:
(а) a2 = |a|2 = 9
(б) (3a - 2b)(a + 2b) = 3a2 - 2ba + 6ab - 4b2 = 3a2 + 4ab - 4b2 =
= 3|a|2 + 4|a||b|cos1200 - 4|b|2 = 3*9 + 4*3*4*(-1/2) - 4*16 =
= 27 - 24 - 64 = -61

29.

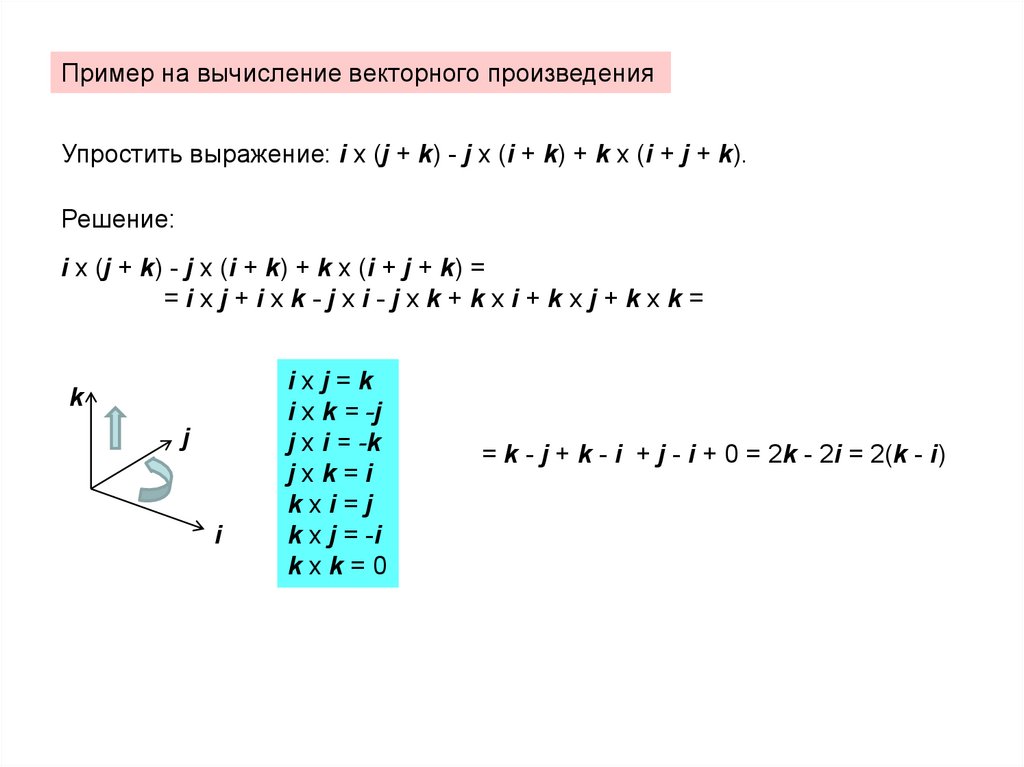
Пример на вычисление векторного произведения
Упростить выражение: i x (j + k) - j x (i + k) + k x (i + j + k).
Решение:
i x (j + k) - j x (i + k) + k x (i + j + k) =
=ixj+ixk-jxi-jxk+kxi+kxj+kxk=
k
j
i
ixj=k
i x k = -j
j x i = -k
jxk=i
kxi=j
k x j = -i
kxk=0
= k - j + k - i + j - i + 0 = 2k - 2i = 2(k - i)