Векторное произведение векторов

1.

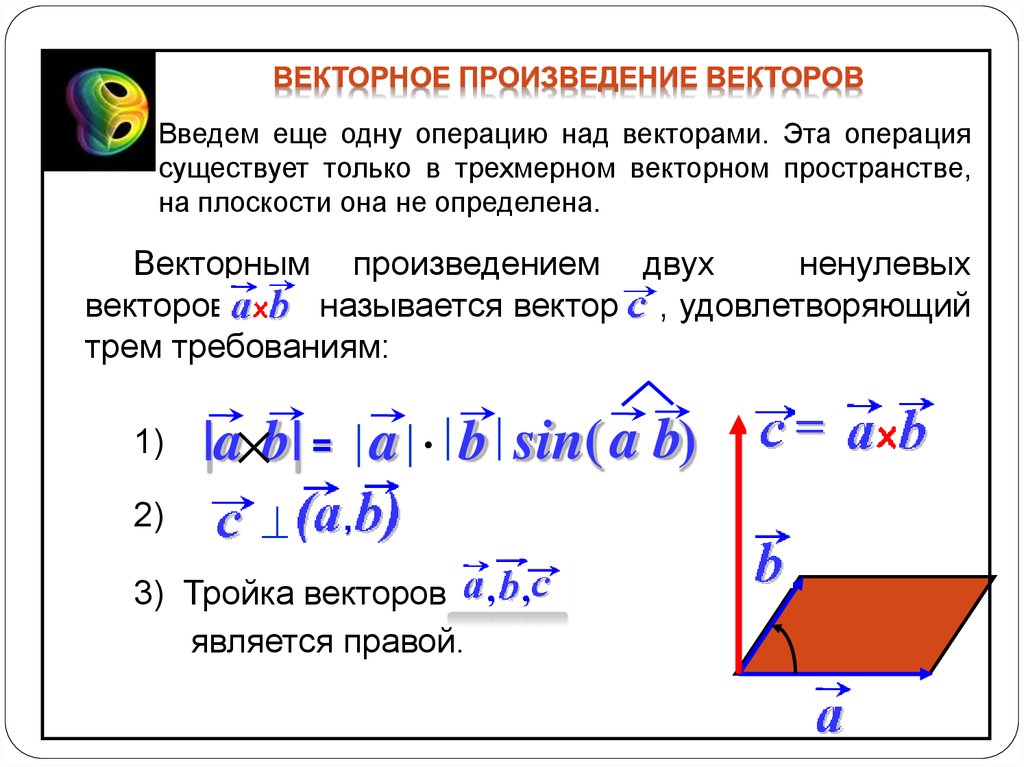
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
Введем еще одну операцию над векторами. Эта операция
существует только в трехмерном векторном пространстве,
на плоскости она не определена.
Векторным произведением двух
ненулевых
векторов
называется вектор , удовлетворяющий
трем требованиям:
1)
|a b| = a b sin( a b)
2)
3) Тройка векторов
является правой.

2.

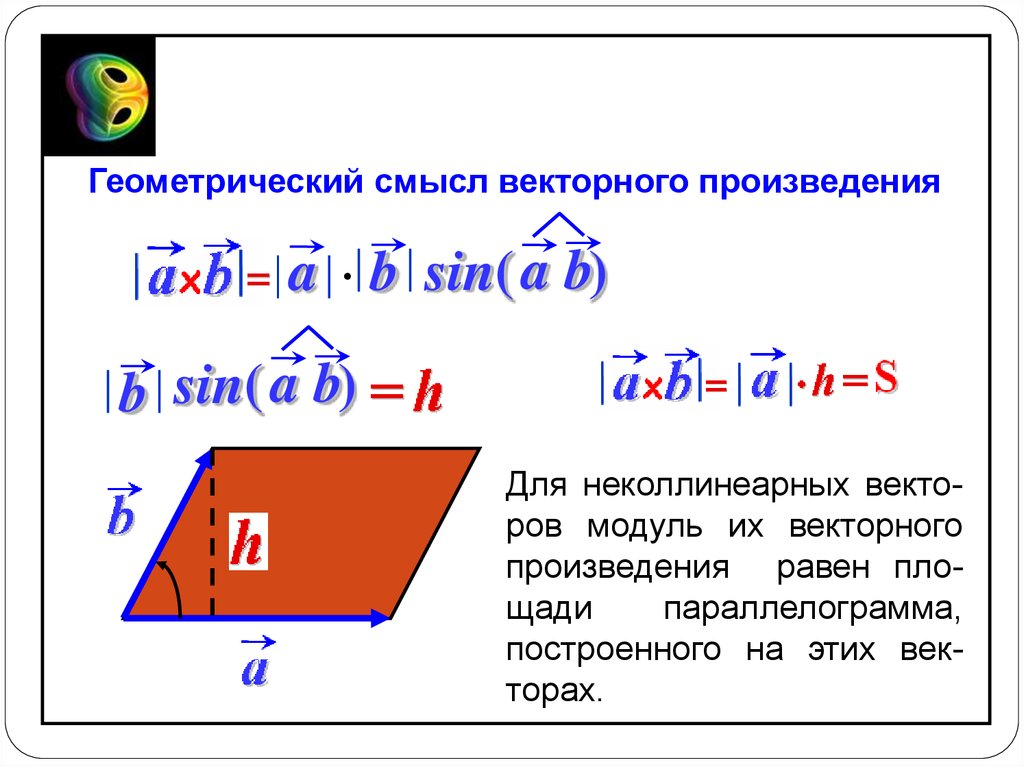
Геометрический смысл векторного произведения
a b sin( a b)
b sin( a b)
Для неколлинеарных векторов модуль их векторного
произведения равен площади
параллелограмма,
построенного на этих векторах.

3.

Свойства векторного произведения
1 ) a b b a.
2) Свойство сочетательности относительно скалярного множителя:
a b a b a b .
3) Распределительное свойство относительно сложения векторов:
a b c a b a c,
a b c d a c b c
a d b d.

4.

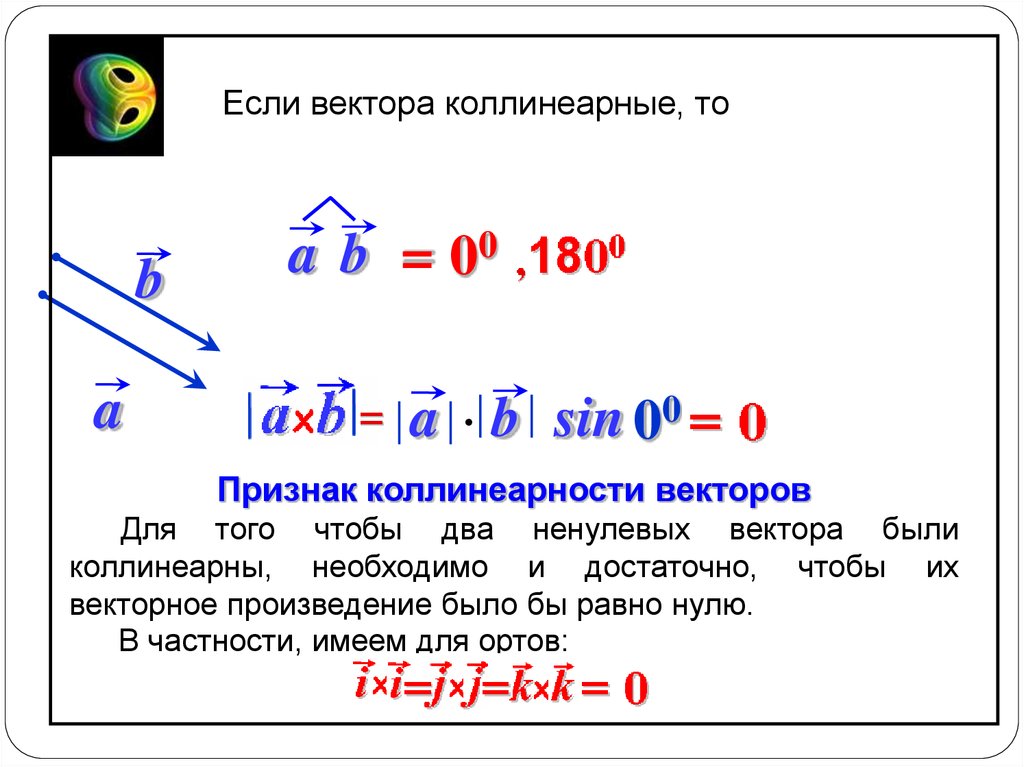
Если вектора коллинеарные, то
b
a
a b = 00
a b sin 00
Признак коллинеарности векторов
Для того чтобы два ненулевых вектора были
коллинеарны, необходимо и достаточно, чтобы их
векторное произведение было бы равно нулю.
В частности, имеем для ортов:

5.

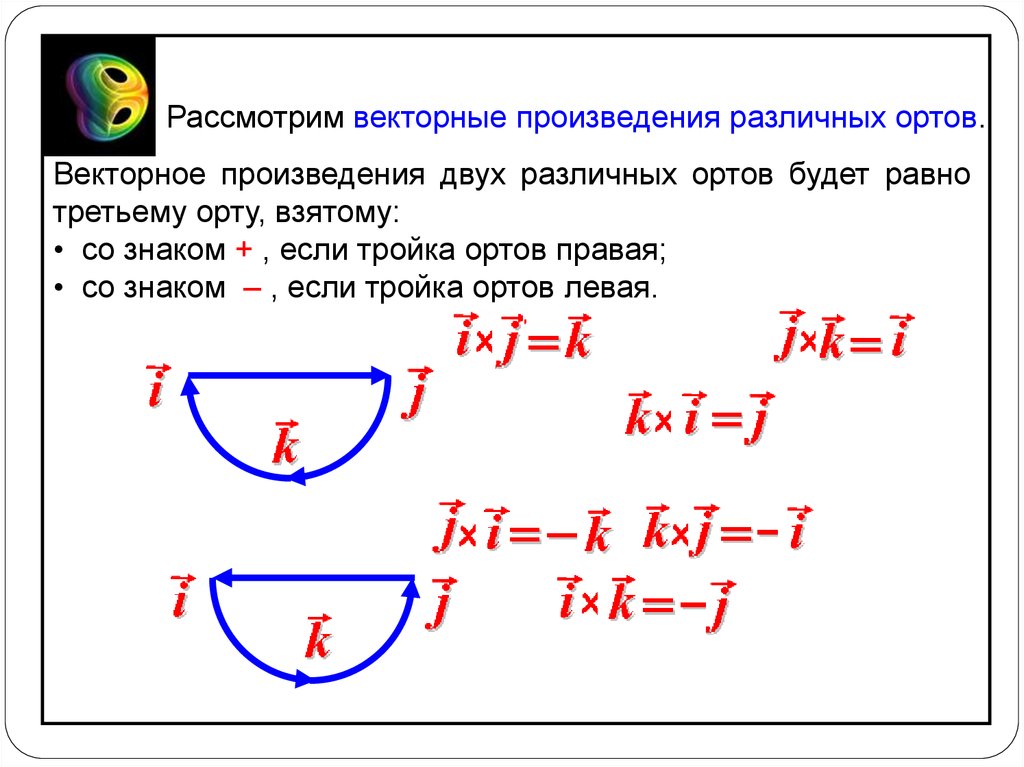
Рассмотрим векторные произведения различных ортов.
Векторное произведения двух различных ортов будет равно
третьему орту, взятому:
• со знаком + , если тройка ортов правая;
• со знаком – , если тройка ортов левая.

6.

Выразим теперь векторное произведение через
координаты векторов, его составляющих.
a b ax i a y j az k bx i by j bz k
axbx i i a ybx j i a z bx k i axby i j a yby j j az by k j
axbz i k a ybk j k a z bz k k
a ybz azby i axbz azbx j axby a ybx k
i
j
k
a b ax
bx
ay
az
by
bz
i
j
k
ax
ay
az
bx
by
bz

7.

Векторное произведение двух векторов позволяет
решить некоторые задачи векторной алгебры.
Нахождение площади параллелограмма и треугольника

8.

Пример 1.
Найти площадь треугольника с вершинами в точках
A(0, 1, 2), B(0, 4, 1), C (2, 1, 1).
Решение
S
1
AB AC ,
2
AB 0, 3, 3 ;
i
j
k
AC 2, 0, 3 .
AB AC 0 3 3 9, 6, 6 ,
2 0 3
AB AC 81 36 36 153 ,
S
1
153
AB AC
6,18
2
2

9.

Пример 2. Найти площадь треугольника, построенного на векторах
Решение
S
1
2a b b ,
2
2a b b 2a b b b 2a b,
1
a
,
b
2
sin
1.
S 2a b a b sin
6
2

10.

Нахождение векторов, перпендикулярных
данной плоскости
Пример 3. Найти единичный вектор, перпендикулярный к плоскости, в
которой лежат точки
A(0, 1, 2), B(0, 4, 1), C (2, 1, 1).
Решение
По определения векторного
произведения векторов
c AB AC
c AB AC.
AB 0, 3, 3 , AC 2, 0, 3 ,
i
j
k
c AB AC 0 3 3 9, 6, 6 ,
2 0 3
Поставленной задаче удовлетворяют два единичных вектора
0
c
9i 6 j 6k
.
153