Похожие презентации:
Матрицы и СЛАУ МНК. (Лекция 5 )
1.
Матрицы и СЛАУ,МНК
Доцент каф. ВМ и М, к.т.н. Каменских А.А.
2.
Матрица размера (m×n) - прямоугольная таблица чисел, каждый элемент которойимеет 2 индекса ( первый - по строке и второй - по столбцу).
Частные случаи
æ1 0 0ö
ç
÷
E = ç0 1 0÷
ç0 0 1÷
è
ø
- единичная матрица – это матрица у которой на главной диагонали 1,
а вне главной диагонали 0.
3.
Действия над матрицамиТРАНСПОНИРОВАНИЕ – это процедура, при применении которой в матрице меняются
местами строки и столбцы. Транспонированная матрица обозначается верхним индексом
«T». Если у исходной матрицы размер (m×n), то у транспонированной матрицы размер
(n×m) .
ТРАНСП(массив)
СЛОЖЕНИЕ - матрицы складываются поэлементно (складываем числа на одинаковых
местах). !!! Складывать можно только матрицы, имеющие одинаковый размер (т.е.
одинаковое число строк и столбцов).
4.
ПЕРЕМНОЖЕНИЕ - матрицы A и B можно перемножать, если число столбцов матрицыA равно числу строк матрицы B. Если матрица A имеет размер (m×k), а матрица B имеет
размер (k×n), то матрица имеет размер (m×n). При этом AB≠BA.
AB = C
å aik bkj = cij
k
æ a11 a12
ç
è a21 a22
МУМНОЖ(массив1; массив2)
æ b11 b12 ö
a13 ö ç
÷ æ c11 c12 ö
÷ * ç b21 b22 ÷ = ç
÷
a23 ø ç
c
c
è
21
22 ø
÷
è b31 b32 ø
Пример:
æ0
ç
ç1
è
1
0
æ1
2ö ç
÷×ç0
1 ÷ø ç
ç1
è
0
1
0
1ö
÷ æ 0 ×1 + 1 × 0 + 2 ×1
0÷ = ç
÷ çè 1 ×1 + 0 × 0 + 1 ×1
1 ÷ø
0 × 0 + 1 ×1 + 2 × 0
1 × 0 + 0 ×1 + 1 × 0
0 × 1 + 1 × 0 + 2 ×1 ö æ 2
÷=ç
1 ×1 + 0 × 0 + 1 ×1 ÷ø çè 2
1
0
2ö
÷
2 ÷ø
5.
Произведением матрицы A на число k называется матрица, у которой каждый элементравен произведению соответствующего элемента матрицы А на число k: kA = kaij
æ1
ç
3×ç 3
ç4
è
-6
0
0
0 ö æ 3 ×1
÷ ç
6 ÷ = ç 3×3
7 ÷ø çè 3 × 4
3 × ( -6 )
3× 0
3×0
3× 0 ö æ 3
÷ ç
3×6 ÷ = ç 9
3 × 7 ÷ø çè12
-18
0
0
0ö
÷
18 ÷
21÷ø
Для суммы и произведения матриц справедливы следующие соотношения:
( A ± B ) × C = A × C ± B × C,
C ( A ± B ) = C × A ± C × B,
A × ( B × C ) = ( A × B ) × C,
( A ± B) ± C = A ± ( B ± C ) .
6.
Обратная матрица-1
-1
-1
Матрица A называется обратной к матрице A, если A A = AA = E
- в результате
их перемножения получается единичная матрица.
!!!Обратная матрица существует, если исходная матрица невырожденная, т.е определитель
не равен нулю. Обратную матрицу можно определить только для квадратных матриц.
МОБР(массив)
Примечание:
Умножение
квадратной
матрицы
любого
соответствующую единичную матрицу не меняет матрицу.
a12 ö æ 1 0 ö æ a11
æ a11
÷×ç
A× E = ç
÷=ç
ç
÷ ç
ça
÷
è 21 a 22 ø è 0 1 ø è a 21
a12 ö æ a11
æ 1 0 ö æ a11
÷=ç
E×A=ç
÷ ×ç
ç0 1÷ ç a
÷ ç
è
ø è 21 a 22 ø è a 21
порядка
на
a12 ö
÷,
a 22 ÷ø
a12 ö
÷.
a 22 ÷ø
Определитель матрицы – это число, характеризующее матрицу. Если определитель
матрицы не равен 0, то говорят, что матрица невырожденная. В противном случае
матрицу называют вырожденной.
!!!Определитель вычисляется только для квадратных матриц.
МОПРЕД(массив)
7.
Определителем матрицы второго порядка, называется число, обозначаемое символомD = det ( A ) =
a11
a12
a 21
a 22
и определяемое равенством
D = a11 × a 22 - a12 × a 21
Подобное определение можно дать и для определителя третьего порядка:
a11
a12
a13
D = det ( A ) = a 21
a 22
a 23 = ( -1)
a31
a32
a33
1+1
a11
a 22
a 23
a32
a33
+ ( -1)
1+ 2
a12
a 21
a 23
a31
a33
+ ( -1)
1+ 3
a13
a21
a 22
a31
a32
D = a11 × a 22 × a33 + a12 × a 23 × a31 + a 21 × a32 × a13 - a13 × a 22 × a31 - a 23 × a32 × a11 - a12 × a 21 × a33
a11
a12
a13
a11
a12
a13
a 21
a 22
a 23
a 21
a 22
a 23
a31
a32
a33
a31
a32
–
a33
+
8.
СИСТЕМЫ ЛИНЕЙНЫХ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ (СЛАУ).НА ПРИМЕРЕ СИСТЕМЫ ИЗ 3-Х УРАВНЕНИЙ С 3-Я
НЕИЗВЕСТНЫМИ
ìa11 x1 + a12 x2 + a13 x3 = h1 ,
ï
( 1)
ía 21 x1 + a 22 x2 + a 23 x3 = h2 ,
ïa x + a x + a x = h .
33 3
3
î 31 1 32 2
*
*
*
Тройка чисел x1 , x 2 , x3 называется решением системы (1), если в результате
подстановки этих чисел вместо x1 , x 2 , x3 все три уравнения (1) обращаются в тождества.
Существует несколько методов решения СЛАУ: метод Крамера, Матричный метод ( метод обратной
матрицы), метод Гаусса.
В Excel мы будем рассматривать первые два метода.
Метод Крамера
В методе Крамера основную роль будут играть следующие четыре определителя:
a11
a12
a13
D = a 21
a 22
a 23
a31
a32
a33
h1
a12
a13
a11
h1
a13
a11
a12
h1
Dx1 = h2
a 22
a 23
Dx 2 = a 21
h2
a 23
Dx3 = a 21
a 22
h2
h3
a32
a33
a31
h3
a33
a31
a32
h3
– главный определитель системы (1)
9.
Если главный определитель системы (1) неравен нулю, то решение системы (1)
существует и единственно.
– решение единственное
V¹ 0
Используя свойства определителей, решение
системы (1) можно записать в виде:
x1 =
Dx1
,
D
x2 =
Dx 2
,
D
x3 =
Dx 3
D
( 2)
МОПРЕД(массив)
– формулы Крамера
Матричная запись системы линейных алгебраических уравнений
ìa11 x1 + a12 x 2 + a13 x3 = h1 ,
ï
ía 21 x1 + a 22 x2 + a 23 x3 = h2 ,
ïa x + a x + a x = h .
33 3
3
î 31 1 32 2
æ a11
ç
A = ç a 21
ç
ça
è 31
a12
a 22
a32
A× X = H
X = A -1 × H
a13 ö
÷
a 23 ÷ ,
÷
a33 ÷ø
æ x1 ö
æ h1 ö
ç ÷
ç ÷
X = ç x 2 ÷ , H = ç h2 ÷
ç ÷
ç ÷
çx ÷
çh ÷
è 3ø
è 3ø
( 3)
( 1)
( 2)
– матричная запись СЛАУ
– решение СЛАУ (3) в матричном виде
МОБР(массив)
МУМНОЖ(мас 1; мас 2)
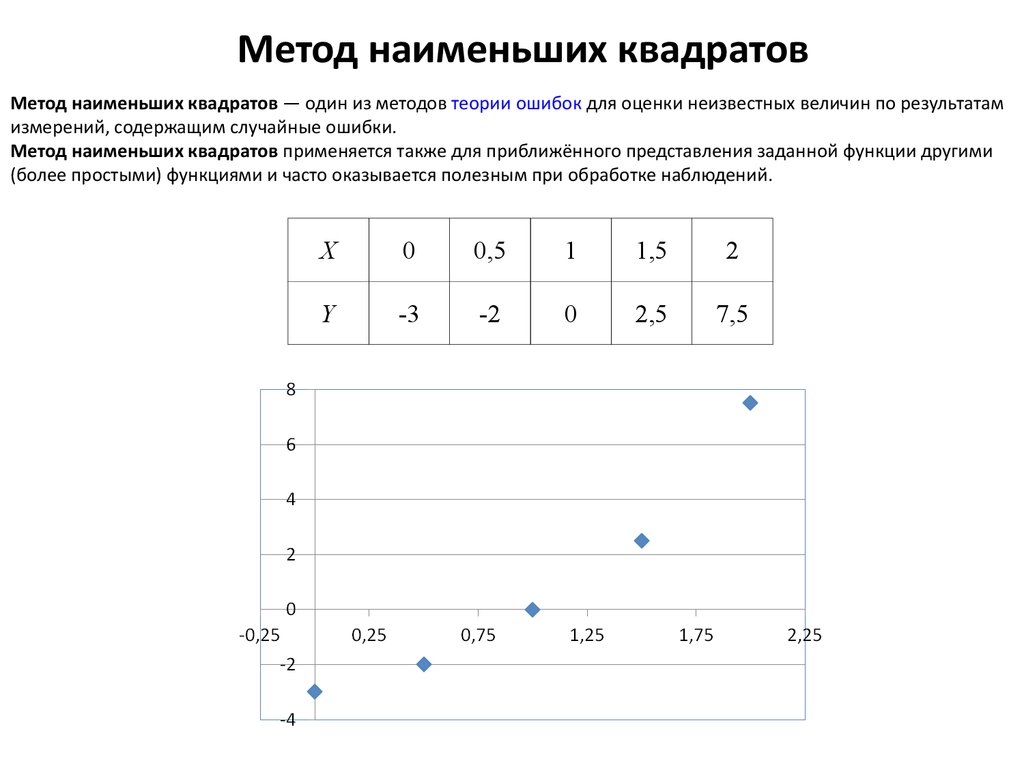
10. Метод наименьших квадратов
Метод наименьших квадратов — один из методов теории ошибок для оценки неизвестных величин по результатамизмерений, содержащим случайные ошибки.
Метод наименьших квадратов применяется также для приближённого представления заданной функции другими
(более простыми) функциями и часто оказывается полезным при обработке наблюдений.
X
0
0,5
1
1,5
2
Y
-3
-2
0
2,5
7,5
11.
Необходимо построить функцию, которая быпроходила наиболее близко к указанным точкам
y%= f ( x, a, b, c ) = a + bx + cx 2
n
n
(
)
Q ( a, b, c ) = å éë y i - y%( xi , a, b, c ) ùû = å é y i - a + bx i + cx i2 ù
ë
û
i =1
i =1
2
xi , yi – координаты заданных точек (данные из таблицы)
n – количество заданных точек
n
å xi = x1 + x2 + x3 + x4 + ... + xn-1 + xn
i =1
2
12.
nì дQ
ï
ï дa
ïï дQ
í
ï дb
ï дQ
ï
ïî дc
Q ( a , b, c ) = å é y i ë
i =1
(
a + bxi + cxi2
) ùû
2
n
n
n
ì
2
ïan + bå xi + c å xi = å y i ,
= -2å éë yi - a - bxi - cxi2 ùû = 0,
i =1
i =1
i =1
ï
i =1
n
n
n
ïï n
n
2
3
= -2å éë yi - a - bxi - cxi2 ùû ( xi ) = 0, ía å xi + bå xi + c å xi = å y i xi ,
i =1
i =1
i =1
ï i =1
i =1
n
n
n
ï n
n
2
3
4
2
= -2å éë yi - a - bxi - cxi2 ùû xi2 = 0. ïa å xi + bå xi + c å xi = å y i xi .
ïî i =1
i =1
i =1
i =1
i =1
n
( )
13.
XY
X2
0
-3
0
0,5
-2
0,25
1
0
1
1,5
2,5
2,25
2
7,5
4
Сумма
5
5
7,5
X3
0
0,125
1
3,375
8
12,5
X4
0
0
0
0,063
-1
-0,5
1
0
0
5,063
3,75
5,625
16
15
30
22,13
17,75
35,13
X×Y
X2×Y
Система уравнений для определения коэффициентов
сглаживающей функции
ì5a + 5b + 7,5c = 5,
ï
í5a + 7,5b + 12,5c = 17, 75,
ï7,5a + 12,5b + 22,13c = 35,13.
î
Конечный вид сглаживающей функции
y%= -2,886 + 0, 243 x + 2, 429 x 2










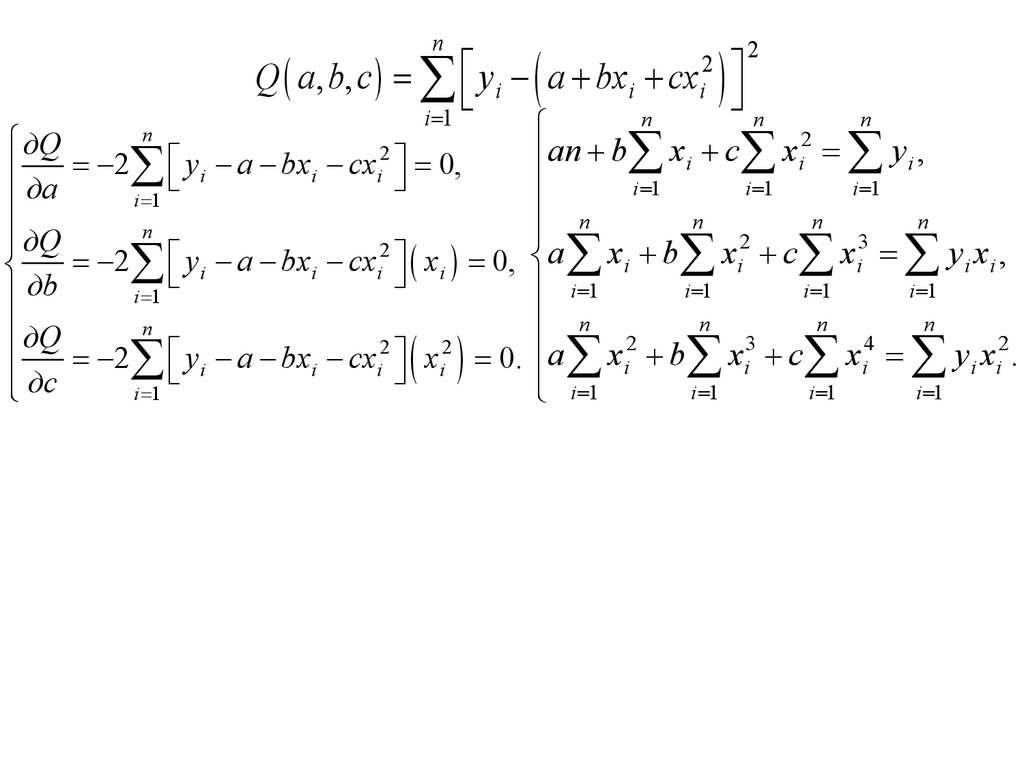


 Математика
Математика








