Обработка данных активного эксперимента

1.

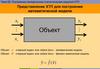
Обработка данных активного эксперимента
Задание: подобрать такие значения температуры и времени
превращения, при которых концентрация промежуточного
продукта была бы максимальной.
Реакция протекает по схеме:
А
Р
S
Q
Планирование эксперимента проводят по схеме:
I этап – ПФЭ
II этап – ОЦКП

2.

I этап – ПФЭ
1. Решение задачи структурной идентификации:
Спром. прод a0 a1T a2
yˆ a0 a1 x1 a2 x2
Производим замену переменных:
~
х z; а а
ŷ a~0 z0 a~1 z1 a~2 z2 , где z 1 или 1
0
zj
xj xj
x j
min
x j 0.5 x max
x
j
j
( j 1, ..., m)
max
x j0 0.5 x min
x
j
j

3.

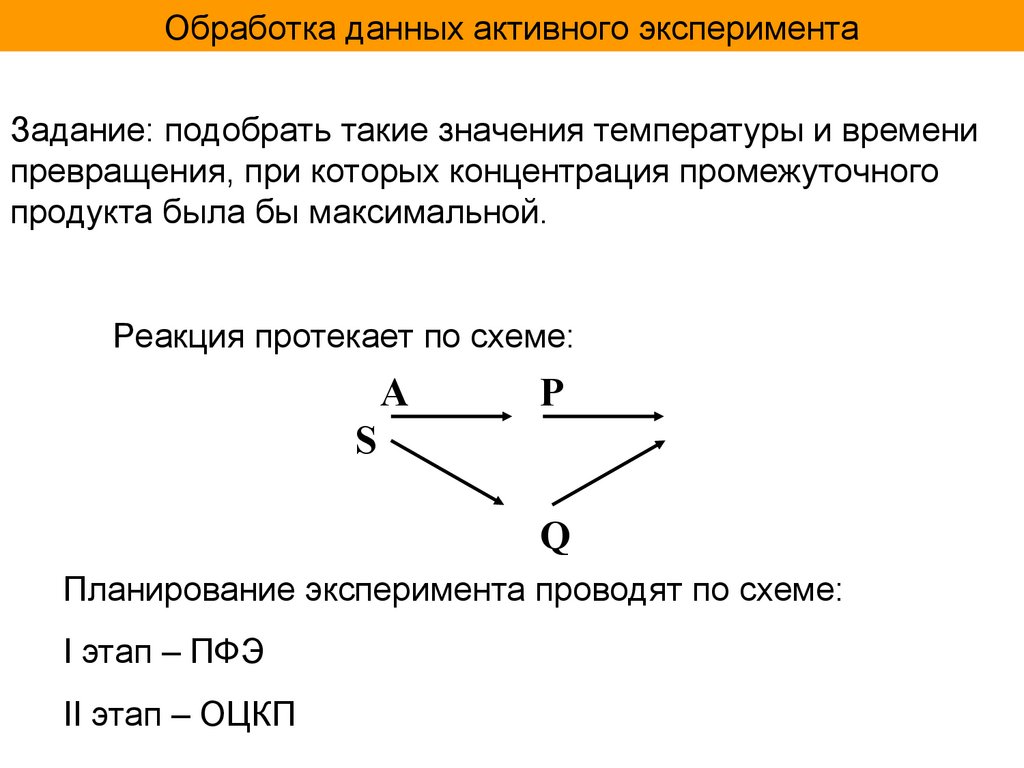
Выбираем
• значение переменной в центре плана: Т(0). = 330 К ; (0) = 75 с
• область изменения переменных: Т = ±10 К; = ± 25 с
• рассчитываем значения некодированных факторов (хj), при которых
должен ставиться эксперимент
и проводим эксперимент

4.

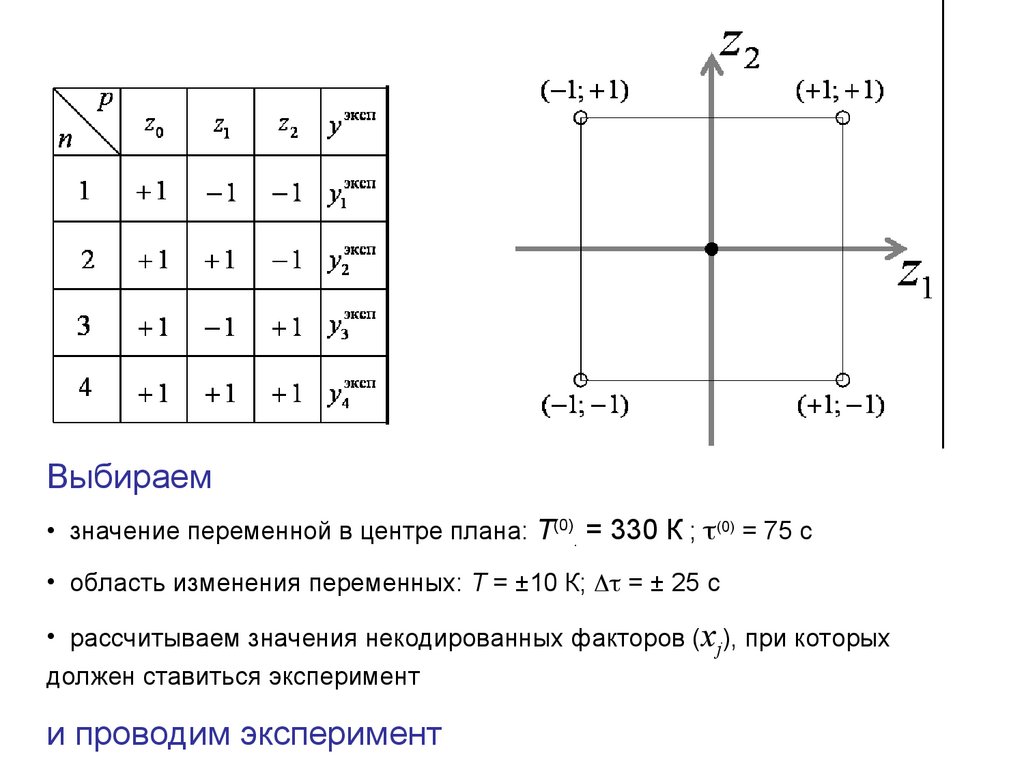
уэксп
Опыты, проводимые по плану ПФЭ:
1
320
50
0,1855
2
340
50
0,0222
3
320
100
0,1098
4
340
100
0,0114
Опыты, проводимые в центре плана:
9
330
75
0,0519
10
330
75
0,0495
11
330
75
0,0475
12
330
75
0,048
13
330
75
0,0519
14
330
75
0,0515

5.

2. Решение задачи параметрической идентификации:
~
~
~
ŷ a0 a1 z1 a2 z 2
урасч
?
?
?
n
эксп
~
a j zij yi
n,
j 0, 1, ..., m
i 1
Производим замену переменных:
у̂1
~
z х; а а
Т 330
75
~
Сi у̂i a0 a1
a2
10
25
Рассчитываем у̂1 , у̂ 2 , у̂3 , у̂4

6.

Определение коэффициентов регрессии для уравнения I порядка

7.

3. Проверка значимости кодированных коэффициентов:
Коэффициент значим, если:
t расч
j
~
a
j
Se
n tβтабл
νe
j 0,1, ..., m
v = 5; р = 0.05
Если условие не выполняется, коэффициент с соответствующим фактором
приравнивается нулю; а урасч пересчитывается.
k
S e2
y
2
(0) эксп
j
y (0) эксп
j 1
k 1
,
y
(0) эксп
k
y S(0) эксп k
S 1

8.

3. Проверка адекватности уравнения:
2
SR
расч
F
2
Se
n
табл
Fβ ν R , ν e ,
ŷ
S R2 i 1
I
i
yiэксп
n p
2
.

9.

Определение остаточной
дисперсии
р – число значимых коэффициентов линеаризованного уравнения
регрессии
fR = 4 – р
Определение дисперсии воспроизводимости
fе = 6 – 1

10.

II этап – ОЦКП
Спром.прод ŷ II a0 a1T a2 a12T a11T 2 a22 2
Производим замену переменных:
ŷ
ΙI
~
х z; а а
2
2
~
~
~
~
~
~
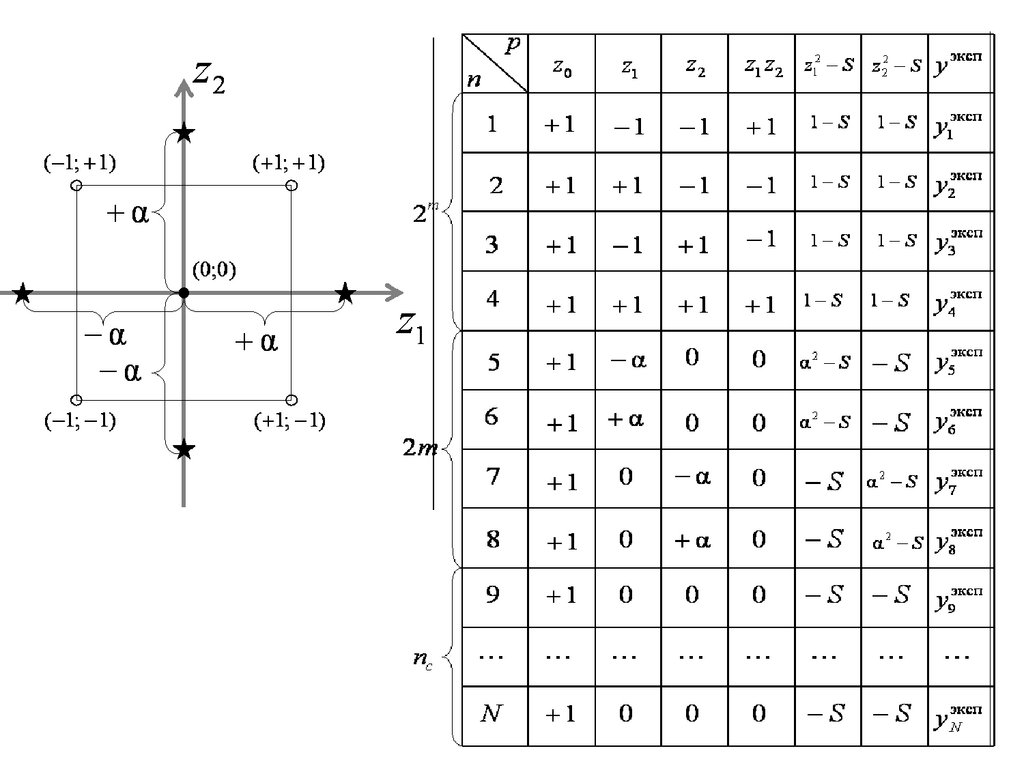
a0 z0 a1z1 a2 z2 a12 z1z2 a11 z1 S a22 z 2 S
n
S
N
n N
α
1 .
2 n

11.

12.

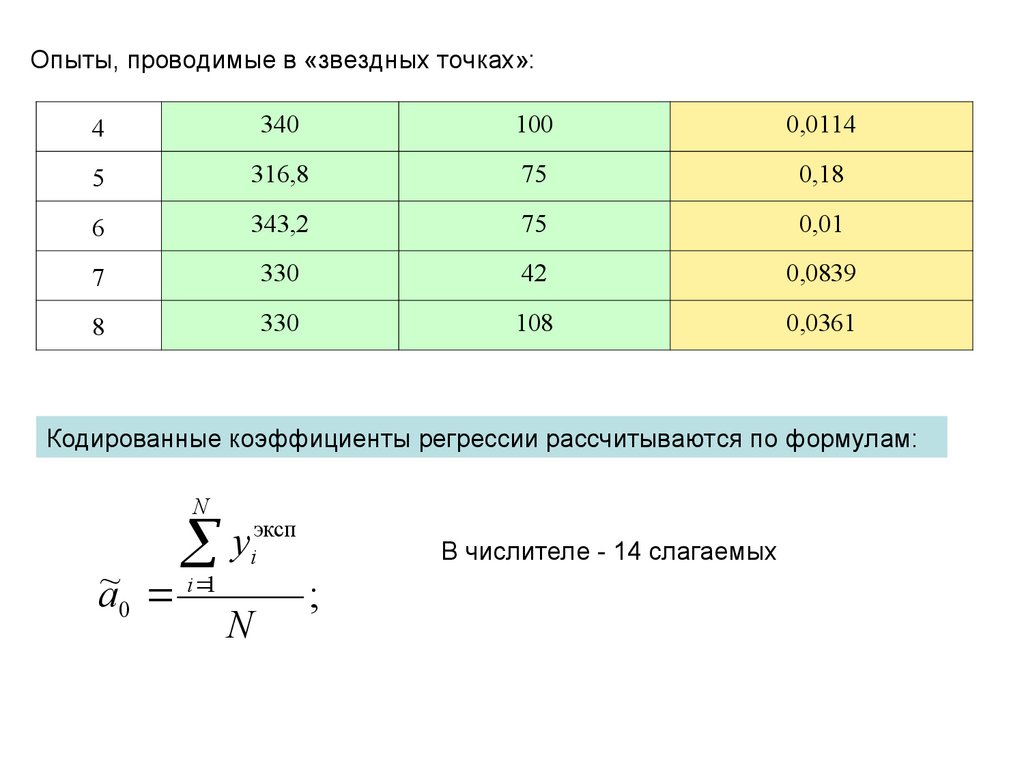
Опыты, проводимые в «звездных точках»:
4
340
100
0,0114
5
316,8
75
0,18
6
343,2
75
0,01
7
330
42
0,0839
8
330
108
0,0361
Кодированные коэффициенты регрессии рассчитываются по формулам:
N
эксп
y
i
a~0 i 1
N
В числителе - 14 слагаемых
;

13.

N
эксп
z
y
ij i
В числителе – 6 слагаемых
~ a
~,a
~ i 1
a
j 1
2
n 2α 2
n
эксп
z
z
y
ij iu i
a~ ju a~12 i 1
, u j
n
N
z
a~ jj a~11 , a~22 i 1
2
ij
В числителе – 4 слагаемых
S yiэксп
2α 4
В числителе - 14 слагаемых

14.

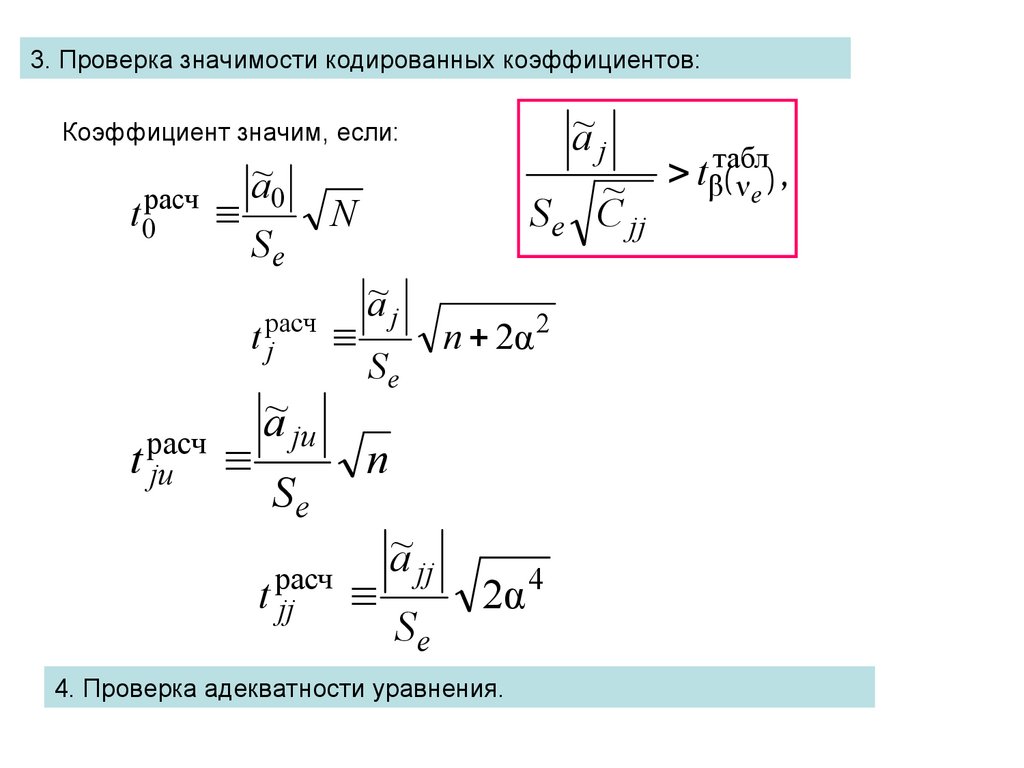
3. Проверка значимости кодированных коэффициентов:
a~ j
табл
t
β νe ,
~
S e C jj
Коэффициент значим, если:
t0расч
a~0
Se
N
t расч
j
расч
t ju
a~ ju
Se
a~ j
Se
n 2α 2
n
t расч
jj
a~ jj
Se
2α 4
4. Проверка адекватности уравнения.

15.

Определение остаточной
дисперсии
р – число значимых коэффициентов линеаризованного уравнения
регрессии
fR = 14 – р
Определение дисперсии воспроизводимости
fе = 6 – 1

16.

Определение оптимальных значений факторов
ŷ II ~ ~
a1 a12 z 2 2a~11 z1 0;
z1
II
ŷ
~ a~ z 2a~ z 0.
a
2
12 1
22 2
z
2
Результат
z opt
1
z 2opt
можно принимать к рассмотрению, если
Перевести значения кодированных факторов в натуральные.

17.

Решение:
~
~
2
a
a
11 12
a~
~
2
a
22
12
opt
~
z
a
1
1
opt a~
z 2 2