Похожие презентации:
Электромагнетизм
1.
3. Электромагнетизм3.6 Проводники. Полупроводники.
Диэлектрики.
3.7 Электрическое поле в проводнике
3.8 Электрическое поле в диэлектрике
3.9 Поле в неоднородной среде и на
границах раздела диэлектриков
3.10 Электрическая емкость проводников
2.
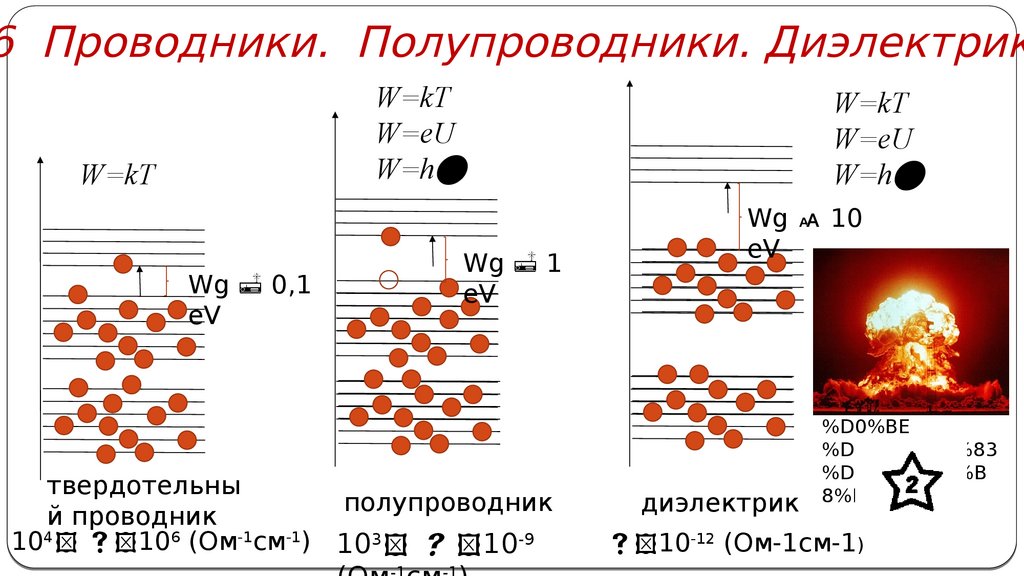
6 Проводники. Полупроводники. ДиэлектрикW=kT
W=eU
W=h
W=kT
Wg 0,1
eV
Wg 1
eV
твердотельны
полупроводник
й проводник
104 106 (Ом-1см-1) 103 10-9
W=kT
W=eU
W=h
Wg 10
eV
диэлектрик
https://
ru.wikipedia.org/
wiki/%D0%AF
%D0%B4%D0%B
5%D1%80%D0%B
D%D0%BE
%D0%B5_
%D0%BE
%D1%80%D1%83
%D0%B6%D0%B
8%D0%B5
10-12 (Ом-1см-1)
3.
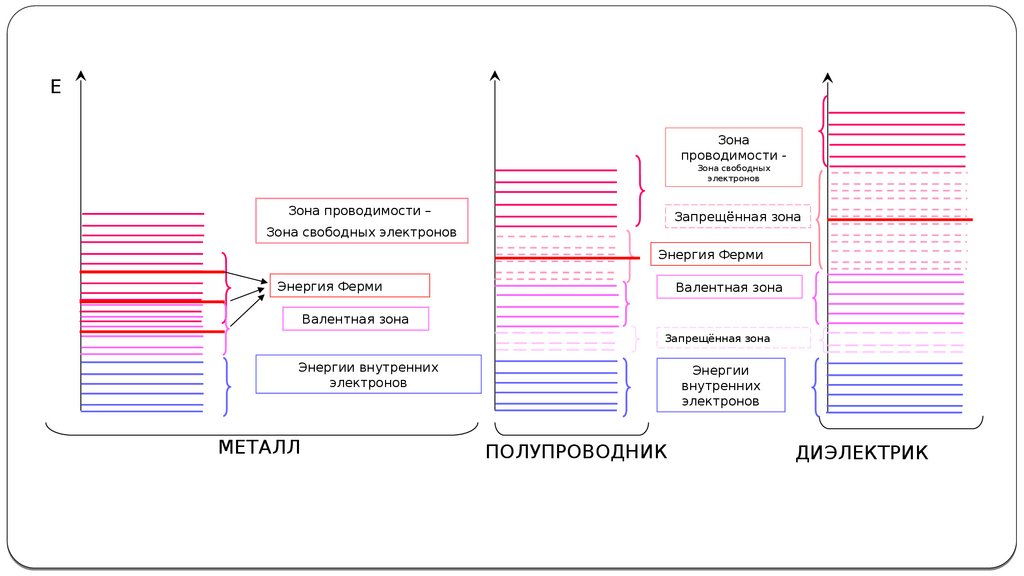
ЕЗона
проводимости Зона свободных
электронов
Зона проводимости –
Запрещённая зона
Зона свободных электронов
Энергия Ферми
Энергия Ферми
Валентная зона
Валентная зона
Запрещённая зона
Энергии внутренних
электронов
МЕТАЛЛ
Энергии
внутренних
электронов
ПОЛУПРОВОДНИК
ДИЭЛЕКТРИК
4.
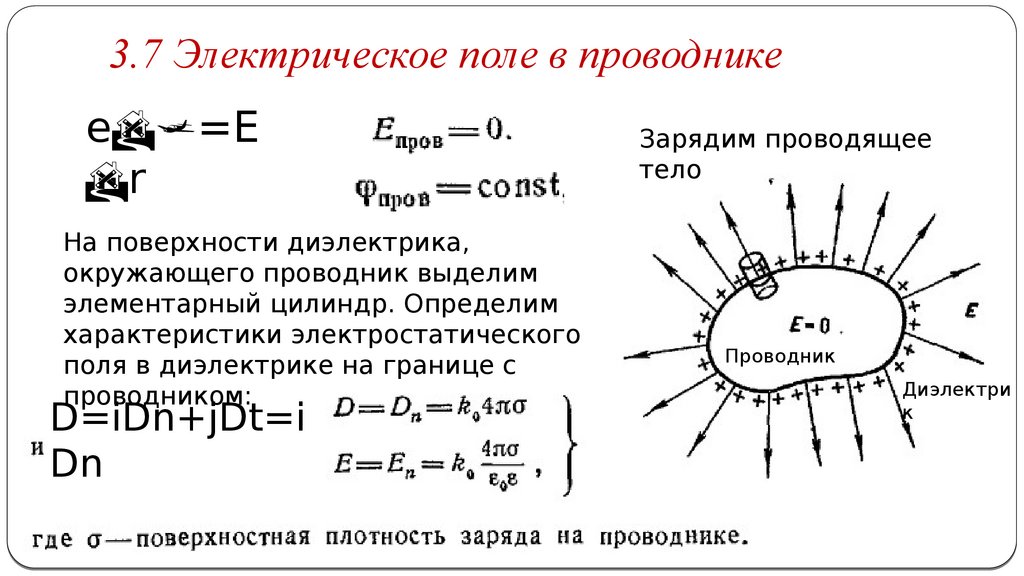
3.7 Электрическое поле в проводникеe =E
r
На поверхности диэлектрика,
окружающего проводник выделим
элементарный цилиндр. Определим
характеристики электростатического
поля в диэлектрике на границе с
проводником:
D=iDn+jDt=i
Dn
Зарядим проводящее
тело
Проводник
Диэлектри
к
5.
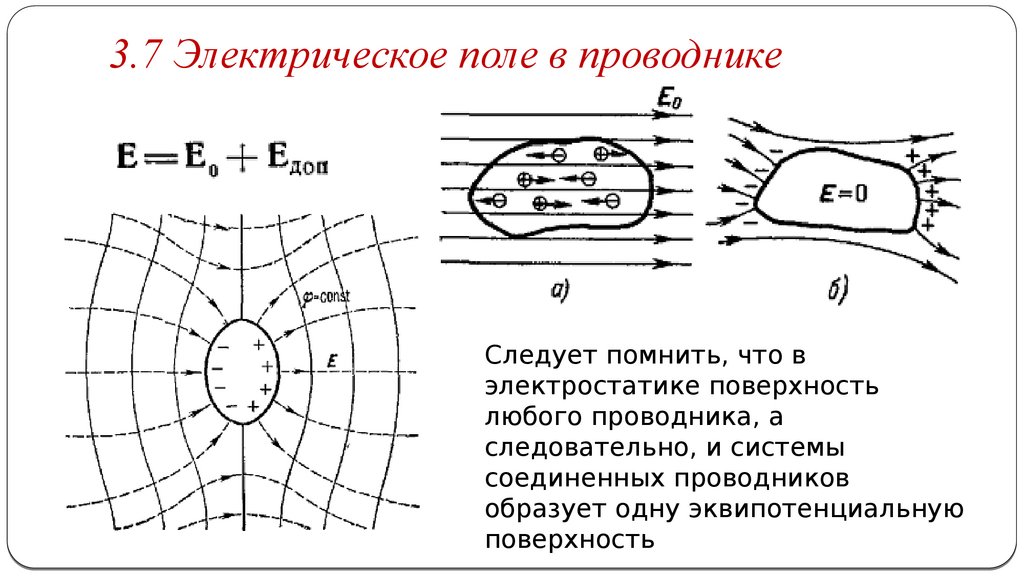
3.7 Электрическое поле в проводникеСледует помнить, что в
электростатике поверхность
любого проводника, а
следовательно, и системы
соединенных проводников
образует одну эквипотенциальную
поверхность
6.
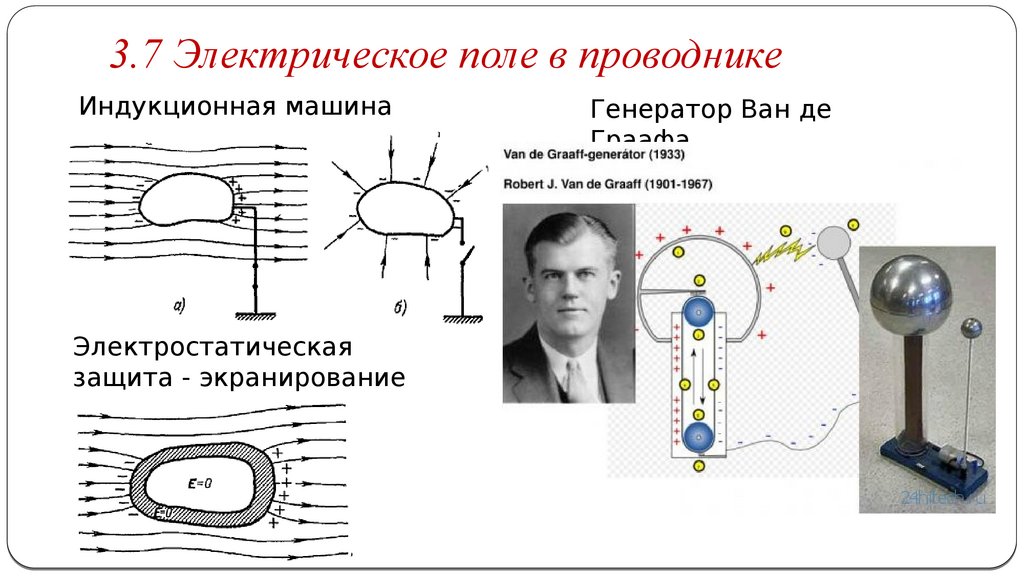
3.7 Электрическое поле в проводникеИндукционная машина
Генератор Ван де
Граафа
https://24hitech.ru/kak-sdelat-generator-van-degraafa-svoimi-rykami.html
Электростатическая
защита - экранирование
7.
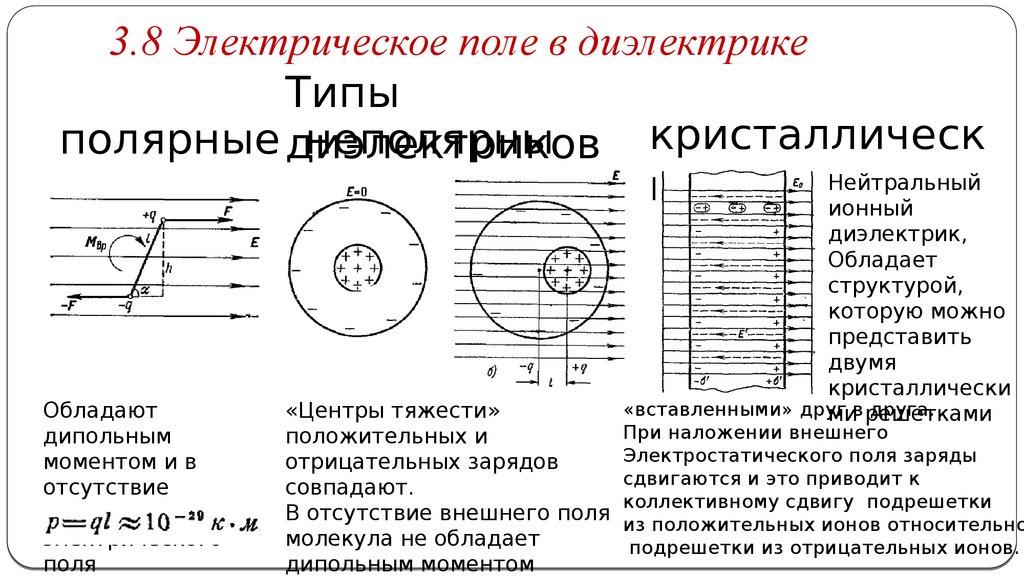
3.8 Электрическое поле в диэлектрикеТипы
кристаллическ
полярные диэлектриков
неполярны
Нейтральный
ие
е
ионный
Обладают
дипольным
моментом и в
отсутствие
внешнего
электрического
поля
«Центры тяжести»
положительных и
отрицательных зарядов
совпадают.
В отсутствие внешнего поля
молекула не обладает
дипольным моментом
диэлектрик,
Обладает
структурой,
которую можно
представить
двумя
кристаллически
«вставленными» друг
друга.
миврешетками
При наложении внешнего
Электростатического поля заряды
сдвигаются и это приводит к
коллективному сдвигу подрешетки
из положительных ионов относительно
подрешетки из отрицательных ионов.
8.
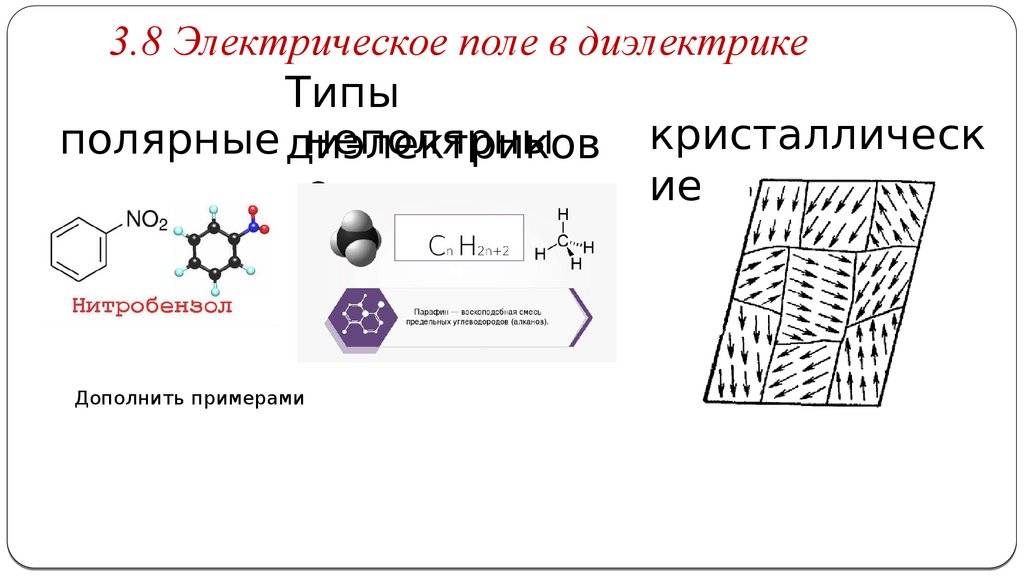
3.8 Электрическое поле в диэлектрикеТипы
кристаллическ
полярные диэлектриков
неполярны
ие
е
Дополнить примерами
9.
3.8.1 Кристаллическиедиэлектрики
10.
3.8.1 Кристаллическиедиэлектрики
= диэлектрическая восприимчивость
11.
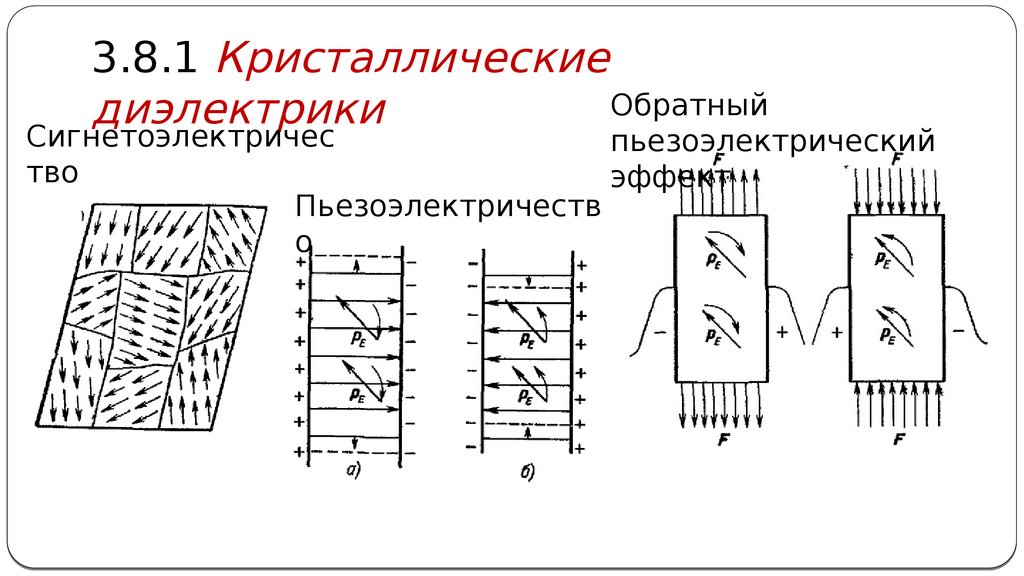
3.8.1 КристаллическиеОбратный
диэлектрики
Сигнетоэлектричес
пьезоэлектрический
тво
эффект
Пьезоэлектричеств
о
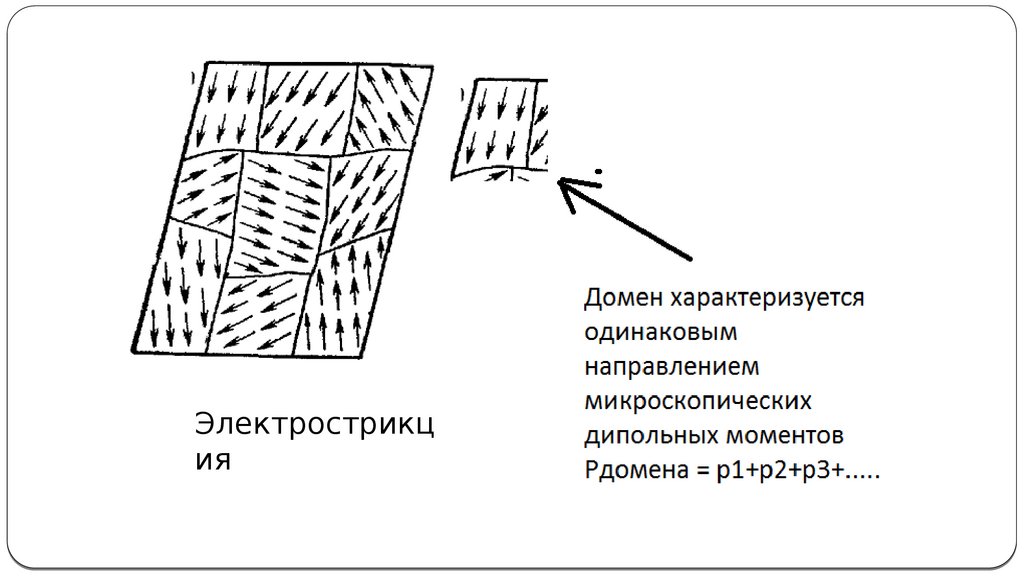
12.
Электрострикция
13.
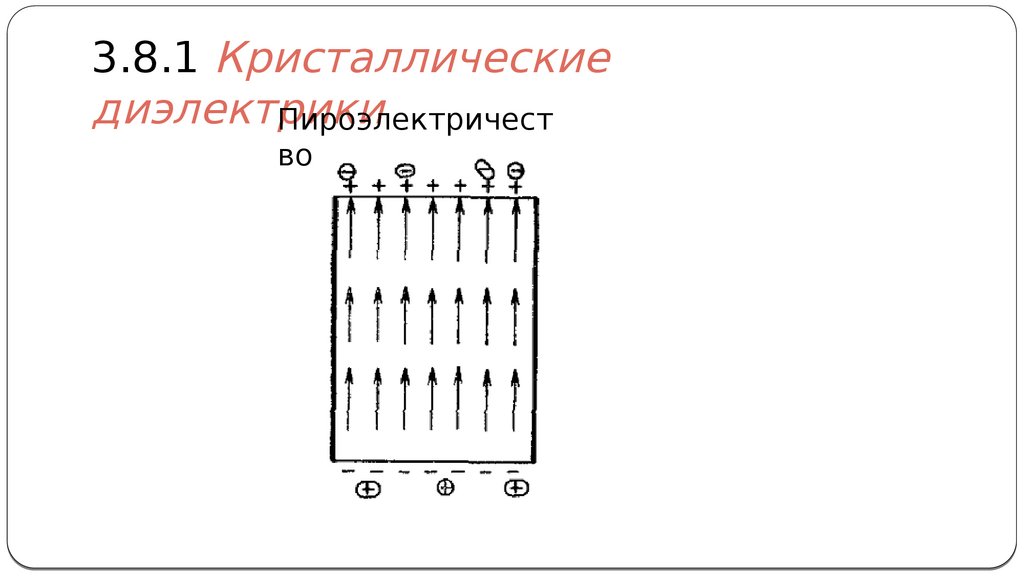
3.8.1 Кристаллическиедиэлектрики
Пироэлектричест
во
14.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
Поле
k0
4 P
плоскопараллель E E0
0
ной пластины
E0
E0
E E0 E '
E
1 4 k0 0
P 0 E
E0
k0
D 0 E 0
D 0 E 4 P
0
P 0 и D 0 E
1 k0 4
15.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
Поле тела
произвольной формы
E E0 E '
На элементарной площадке
диэлектрика , граничащего с
вакуумом сосредотачивается
заряд с поверхностной плотностью
’
Обозначим P - вектор поляризации
этом
участке. к этой тонкой площадке
По
отношению
следует понимать
E0
как поле, созданное Как внешними зарядами, так и зарядами
самой среды расположенными на противоположном конце
16.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
На расстояниях малых от
поверхности, можно считать ее
плоской и вычислить E’ для
бесконечной плоскости,
заряженной с поверхностной
плотностью ’=P. Линии этого
поля будут перпендикулярны к
поверхности по обе стороны от
нее и направлены в
противоположных
направлениях.
В диэоектрике
Полное поле в вакууме
В вакууме
17.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
18.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
Ранее мы предполагали, что линии поля и
направление вектора поляризации к границе
раздела перпендикулярны.
В общем случае, когда линии поля не
перпендикулярны к границе раздела,
соотношение
остается
справедливым только для нормальных
составляющих вектора D:
личными
На границе двух диэлектриков с раз
1
2
диэлектрическими проницаемостями
и
при наличии внешнего поля возникают
' 2 разного знака с
'1 заряды
поляризационные
19.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
Дополнительное поле, создаваемое этими
зарядами, перпендикулярно поверхности,
E2
E 1 составляющие
поэтому нормальные
полей
и
в обеих средах у границы раздела
различны, а касательные составляющие
одинаковы, то естьE т 1 E т 2
Векторы электростатической индукции в
обеих средах соответственно равны
D 1 0 1E 1 и D 2 0 2 E 2
Аналогично случаю границы «диэлектрик – вакуум» нормальная
составляющая вектора индукции на границе двух диэлектриков
остается непрерывной
D
D
E
E
т1
т 2
1
т1
2
т 2
20.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
2 1
На рисунке изображен случай
При этом
E т 2 E т1
.
и линии вектора E при переходе через
границу раздела преломляются, отклоняясь
от перпендикуляра к границе раздела. На
такой границе
D t1
D t2
2
1
1
D t 2 D t1
2
При
и
.
При переходе через границу раздела из
значением
нормальная
вектора D остается
диэлектрика
с меньшимсоставляющая
значением в
неизменной,
касательная увеличивается так, что линии индукции
диэлектрик сабольшим
21.
3.9 Поле в неоднородной среде и на границахраздела диэлектриков
Линии индукции преломляются в данном
случае под тем же углом, что и линии
напряженности поля.
Таким образом, при переходе через
границу раздела двух диэлектриков
изменяется не только вектор
напряженности электрического поля E но и
вектор электростатической индукции D.
Однако поток индукции
через
Dn S
произвольную площадку S на границе
С обеих сторон поверхности остается неизменным.
раздела
Следовательно, число линий индукции, переходящих через
границу, не меняется. И теорема Гаусса остается справедливой
для вектора D в самом общем случае диэлектриком любых форм
22.
3.10 Электрическая емкость проводниковqi
ri
E M Ei k0
2
0 ri ri
i
i
qi
M i k0
0 ri
i
i
q ' nq
q 'i
nq 'i
q'i
'M 'i k0
k0
n k0
n i
0 ri
0 ri
0 ri
i
i
i
i
i
23.
3.10 Электрическая емкость проводниковq'i
nq 'i
q 'i
'M 'i k0
k0
n k0
n i
0 ri
0 ri
0 ri
i
i
i
i
i
То есть потенциал в каждой точке возрастает прямо
пропорционально заряду проводника. Это утверждение конечно
справедливо и для всех точек внутри и на поверхности
проводника, потенциал которых одинаков. Обозначая потенциал
самого проводника через , этот вывод можно выразить
формулой
q С
где
С-
q
С
электрическая емкость проводника
Изменим
q заряд
q проводника
С на
q
, тогда
егоq потенциал
С
возрастет на
24.
3.10 Электрическая емкость проводниковq С
при
q 1
С
q
Откуда следует определение единицы измерения электрической
емкости:
Электроемкость проводника численно равна величине заряда,
который нужно сообщать данному проводнику для увеличения
его потенциала на единицу.
В СГС системе
В системе СИ
1 фарада=1ф, чаще используются миллионные доли фарад – микрофарад и еще
меньшие - нанофарад
25.
3.11 Энергия электрического поля26.
ЛитератураГ.А. Зисман, О.М. Тодес. Курс общей физики. Том
II Электричество и магнетизм М.: Наука, 1972, 366
с.
С.Г. Калашников Электричество М.: ФизМатЛит,
2003, 624
















 Физика
Физика








