Похожие презентации:
Теорема Остроградского-Гаусса
1.
ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА2.1. Силовые линии электростатического поля
2.2. Поток вектора напряженности
2.3. Теорема Остроградского-Гаусса
2.4. Дифференциальная форма теоремы ОстроградскогоГаусса
2.5. Вычисление электростатических полей с помощью
теоремы Остроградского-Гаусса
2.5.1. Поле бесконечной однородно заряженной
плоскости
2.5.2. Поле двух равномерно заряженных плоскостей
2.5.3. Поле заряженного бесконечного цилиндра (нити)
2.5.4. Поле двух коаксиальных цилиндров с одинаковой
линейной плотностью заряда, но разным знаком
2.5.5. Поле заряженного пустотелого шара
2.5.6. Поле объемного заряженного шара
1
2. 2.1. Силовые линии электростатического поля Теорема Остроградского-Гаусса устанавливает связь между электрическими зарядами и
электрическим полем.Она представляет собой более общую и более
изящную формулировку закона Кулона
2
3.
• Остроградский Михаил Васильевич(1801 – 1862)
• отечественный математик и механик.
Учился в Харьковском ун-те (1816 –
1820), совершенствовал знания в
Париже (1822 – 1827).
• Основные работы в области
математического анализа,
математической физики,
теоретической механики. Решил ряд
важных задач гидродинамики, теории
теплоты, упругости, баллистики,
электростатики, в частности задачу
распространения волн на поверхности
жидкости (1826 г.). Получил
дифференциальное уравнение
распространения тепла в твердых
телах и жидкостях. Известен теоремой
Остроградского-Гаусса в
электростатике (1828 г.).
3
4.
• Гаусс Карл Фридрих (1777 – 1855)немецкий математик, астроном и физик.
• Исследования посвящены многим разделам
физики.
• В 1832 г. создал абсолютную систему мер
(СГС), введя три основных единицы: единицу
времени – 1 с, единицу длины – 1 мм, единицу
массы – 1 мг.
• В 1833 г. совместно с В. Вебером построил
первый в Германии электромагнитный
телеграф.
• Еще в 1845 г. пришел к мысли о конечной
скорости распространения электромагнитных
взаимодействий. Изучал земной магнетизм,
изобрел в 1837 г. униполярный магнитометр, в
1838 г. – бифилярный. В 1829 г.
• Сформулировал принцип наименьшего
принуждения (принцип Гаусса).
• Один из первых высказал в 1818 г.
предположение о возможности существования
неевклидовой геометрии.
4
5.
• силовые линии – это линии, касательная ккоторым в любой точке поля совпадает с
направлением вектора напряженности
5
6.
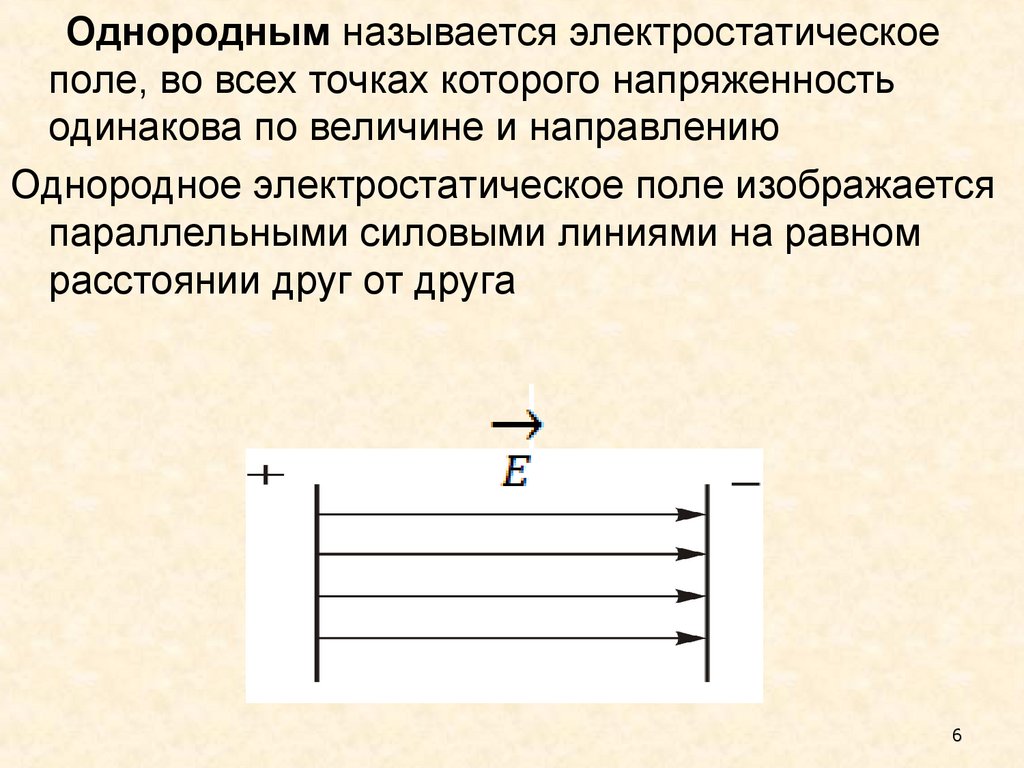
Однородным называется электростатическоеполе, во всех точках которого напряженность
одинакова по величине и направлению
Однородное электростатическое поле изображается
параллельными силовыми линиями на равном
расстоянии друг от друга
6
7.
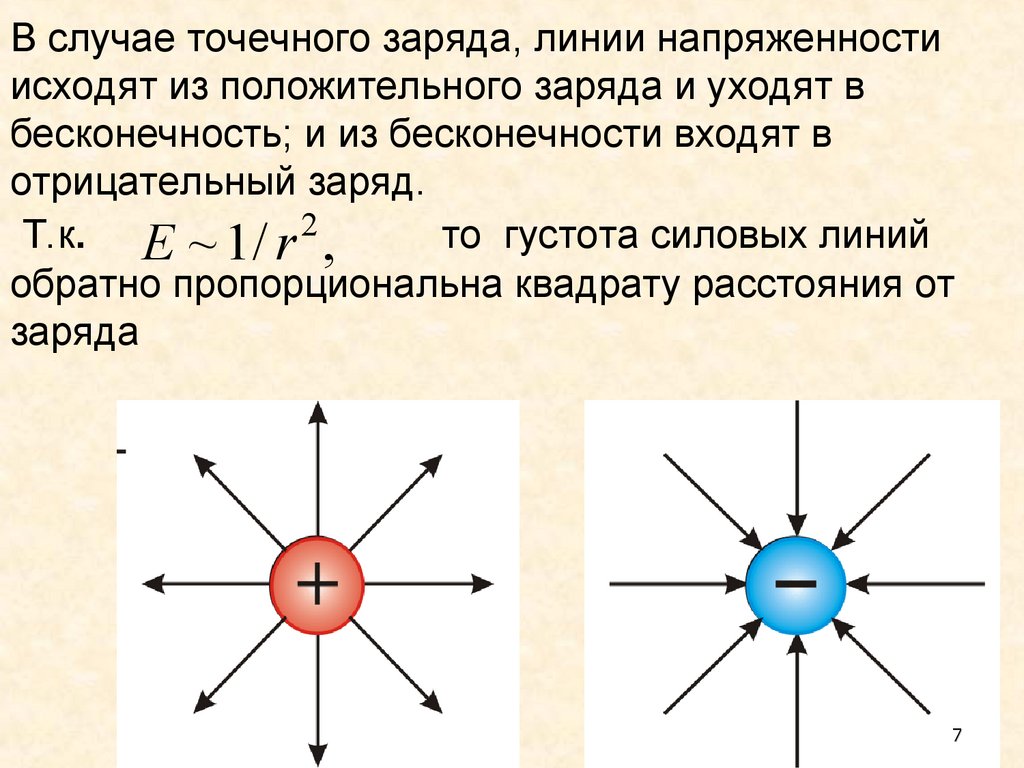
В случае точечного заряда, линии напряженностиисходят из положительного заряда и уходят в
бесконечность; и из бесконечности входят в
отрицательный заряд.
Т.к. Е ~ 1 / r 2 ,
то густота силовых линий
обратно пропорциональна квадрату расстояния от
заряда
7
8.
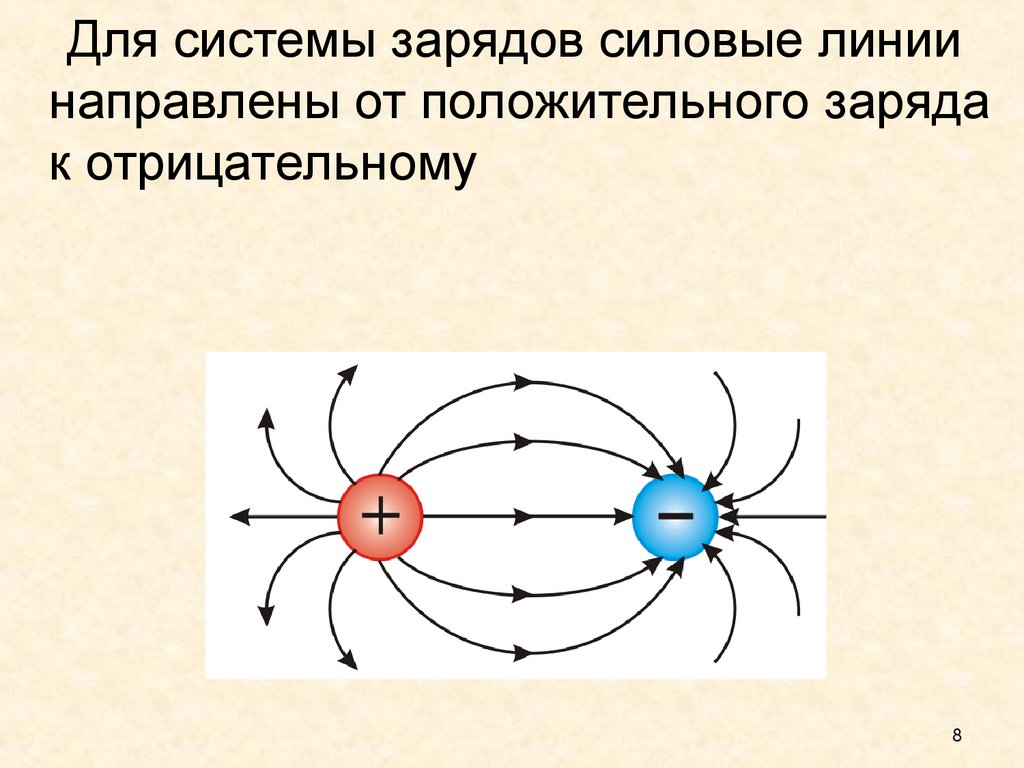
Для системы зарядов силовые линиинаправлены от положительного заряда
к отрицательному
8
9.
910.
Густота силовых линий должна быть такой,чтобы единичную площадку, нормальную к
вектору напряженности пересекало такое их
число, которое равно модулю вектора
напряженности Е , т.е.
число линий Ф
Е
.
S
S
10
11.
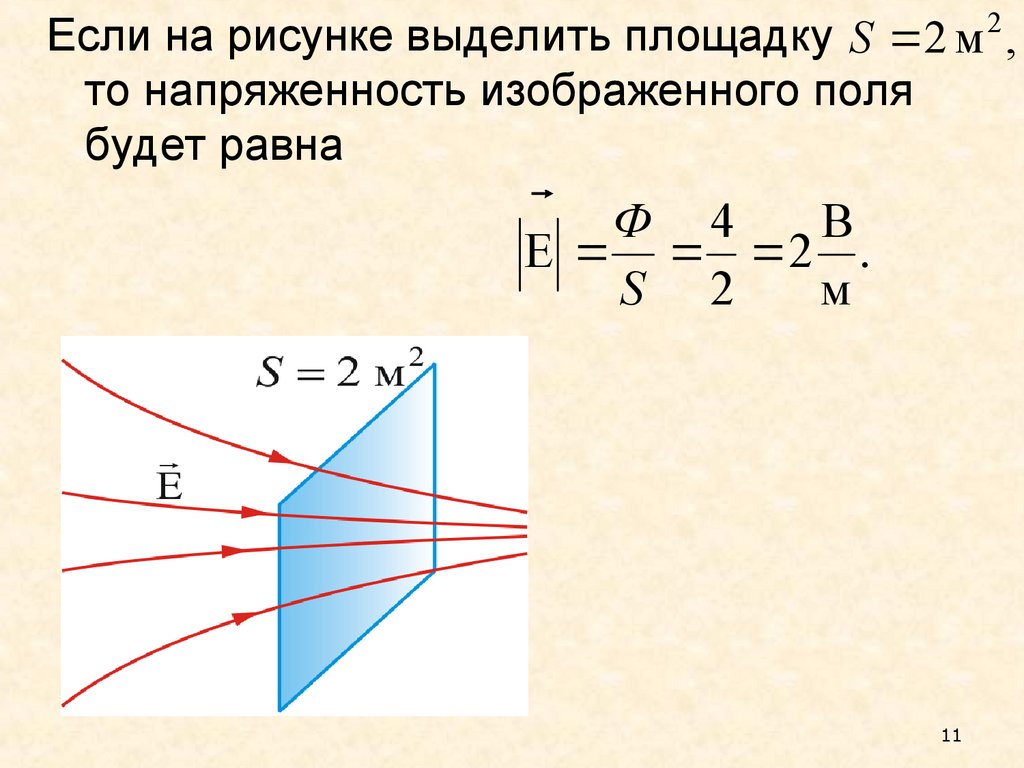
Если на рисунке выделить площадку S 2 м 2 ,то напряженность изображенного поля
будет равна
Ф 4
B
E 2 .
S 2
м
11
12.
2.2. Поток вектора напряженности• Полное число силовых линий, проходящих
через поверхность S называется потоком
вектора напряженности Ф через эту
поверхность
• В векторной форме можно записать
ФЕ Е, S
– скалярное произведение двух векторов, где
вектор.
S nS
12
13.
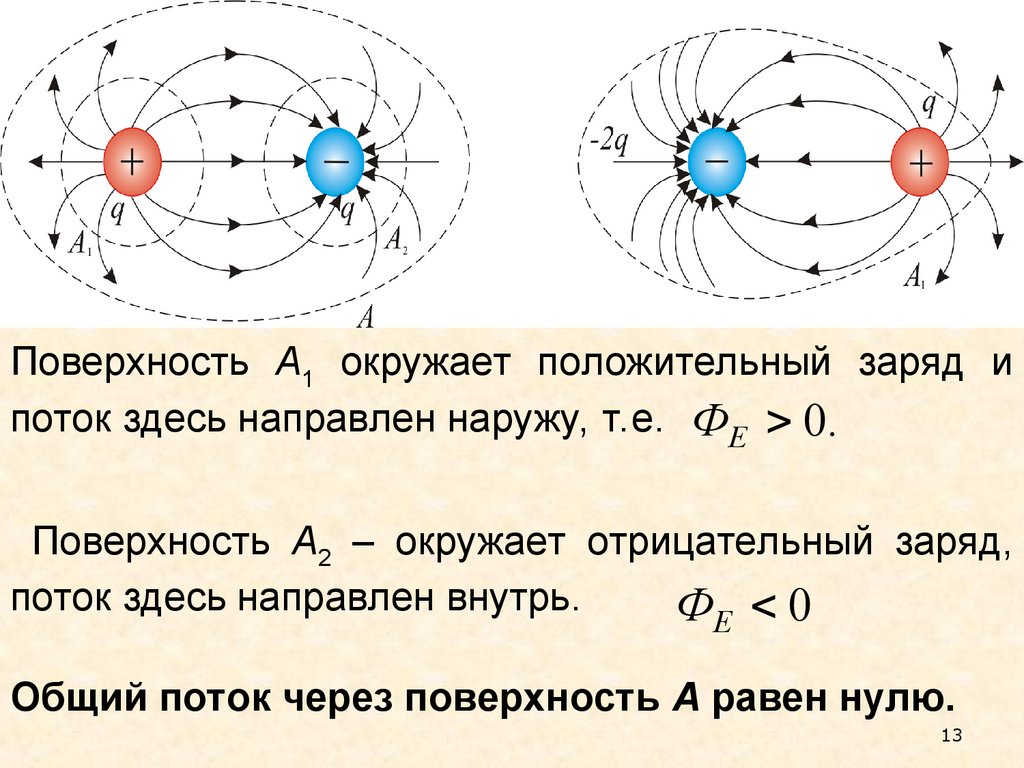
Поверхность А1 окружает положительный заряд ипоток здесь направлен наружу, т.е. ФE 0.
Поверхность А2 – окружает отрицательный заряд,
поток здесь направлен внутрь.
Ф 0
Е
Общий поток через поверхность А равен нулю.
13
14.
2.3. Теорема ОстроградскогоГаусса• Поток вектора напряженности через
произвольную элементарную площадку dS
будет равен:
dФЕ ЕdS cos En dS .
• В однородном поле
ФЕ ES .
• В произвольном электрическом поле
ФЕ Еn dS EdS.
S
S
14
15.
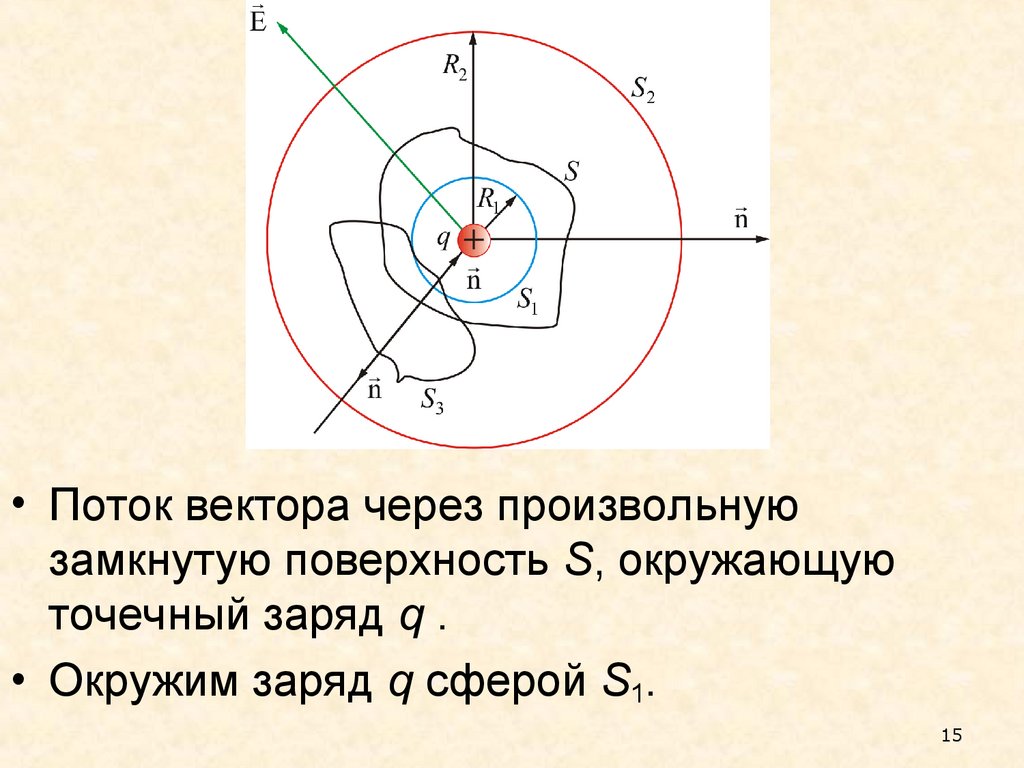
• Поток вектора через произвольнуюзамкнутую поверхность S, окружающую
точечный заряд q .
• Окружим заряд q сферой S1.
15
16.
• Центр сферы совпадает сцентром заряда. Радиус
сферы S1 равен R1.
• В каждой точке поверхности
S1 проекция Е на
направление внешней
нормали одинакова и равна
1 q
En
.
2
4 0 R1
Тогда поток через S1
q
q
2
ФE En dS
4 R1 .
2
4 0 R1
0
S1
q
ФE .
0
16
17.
Поток через сферу S2, имеющуюрадиус R2:
q
q
q
2
ФЕ
dS
4 R2 .
2
2
4 0 R2
4 0R2
0
S2
q
ФЕ .
0
17
18.
• Из непрерывности линии следует, что поток ичерез любую произвольную поверхность S будет
равен этой же величине:
q
ФЕ Еn dS
0
S
– теорема Гаусса для одного заряда.
18
19.
Для любого числа произвольнорасположенных зарядов, находящихся
внутри поверхности:
ФЕ
q
Е dS
n
S
0
– теорема Гаусса для нескольких зарядов:
Поток вектора напряженности электрического поля
через замкнутую поверхность в вакууме равен
алгебраической сумме всех зарядов,
расположенных внутри поверхности, деленной на
ε0.
19
20.
Полныйпоток
проходящий
через
охватывающую заряд q, равен нулю:
S3,
не
Ф3 0
• Таким образом, для точечного заряда q,
полный поток через любую замкнутую
поверхность S будет равен:
q
ФЕ
0 – если заряд расположен внутри
замкнутой поверхности;
• ФЕ 0 – если заряд расположен вне
замкнутой поверхности
20
21.
Электрические заряды могут быть «размазаны» снекоторой объемной плотностью различной в
разных местах пространства:
dq / dV
• Суммарный заряд объема dV будет равен:
q dV .
i
V
• Тогда из теоремы Гаусса можно получить:
1
ФE ЕdS dV
ε0 V
S
1
ФE dV
ε0 V
21
22. 2.4. Дифференциальная форма теоремы Остроградского-Гаусса
Пусть заряд распределен в пространстве V,с объемной плотностью . Тогда
q
EdS ε 0
V
EdS 0
1
EdS
V
0
22
23.
• При V 0или
.
0
0
• Величину, являющуюся
пределом
отношения ЕdS к V, при V 0 ,
называют дивергенцией поля Е
div E
23
24.
Дивергенция поля Е1 .
divE lim
V 0
V
E
d
S
• Дивергенция - скалярная функция
координат.
• В декартовой системе координат
E x E y E z
div E
.
x
y
z
24
25.
Таким образомdiv E .
0
Это теорема Остроградского-Гаусса в
дифференциальной форме.
Введем векторный дифференциальный
оператор (Набла)
i
j k,
x
y
z
где i, j, k – орты осей (единичные векторы).
25
26.
• Сам по себе оператор смысла не имеет. Онприобретает смысл в сочетании с векторной или
скалярной функцией, на которую символично
умножается:
E x E y E z
Е x E x y E y z E z
x
y
z
• дифференциальная форма теоремы
Остроградского-Гаусса.
E
0
26
27.
• В тех точках поля, где div E 0 – источникиполя (положительные заряды),
• В тех точках поля, где div E 0 – стоки
(отрицательные заряды).
• Линии напряженности выходят из источников и
заканчиваются в стоках.
27
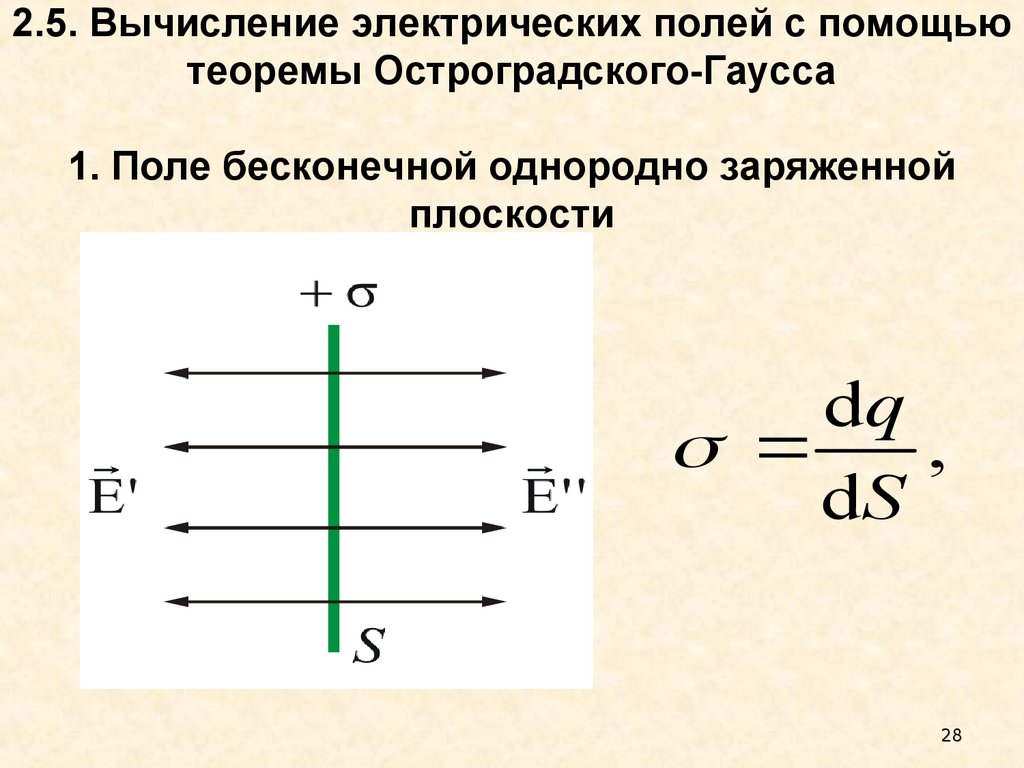
28. 2.5. Вычисление электрических полей с помощью теоремы Остроградского-Гаусса 1. Поле бесконечной однородно заряженной плоскости
dq,
dS
28
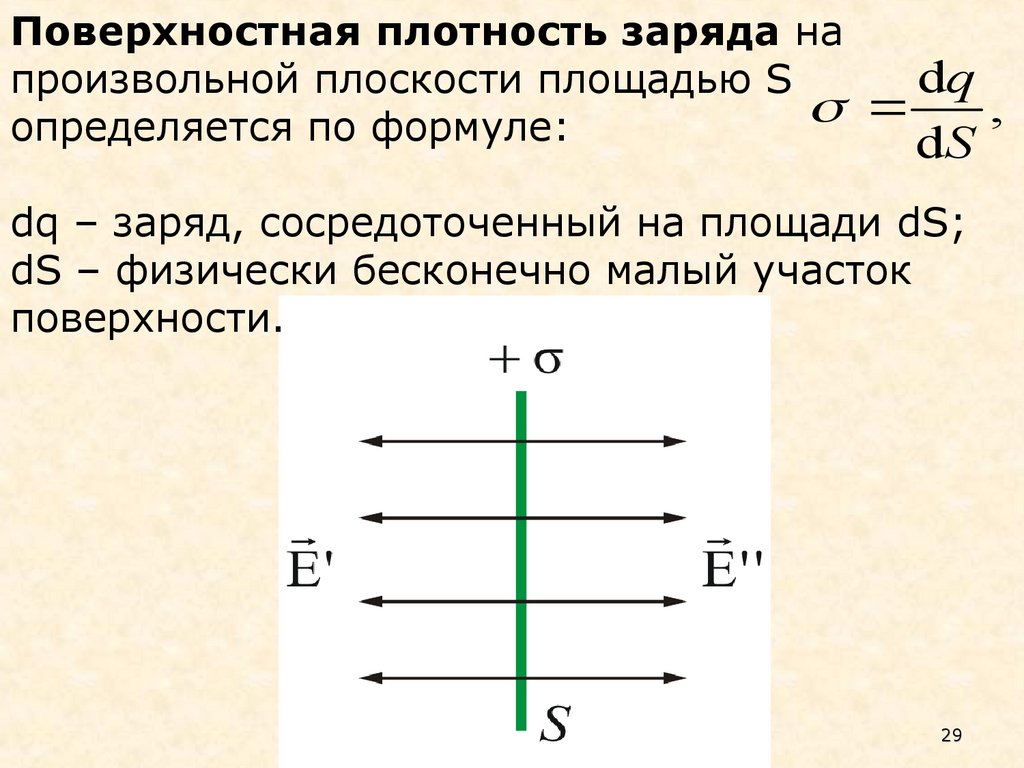
29.
Поверхностная плотность заряда наdq
произвольной плоскости площадью S
,
определяется по формуле:
dS
dq – заряд, сосредоточенный на площади dS;
dS – физически бесконечно малый участок
поверхности.
29
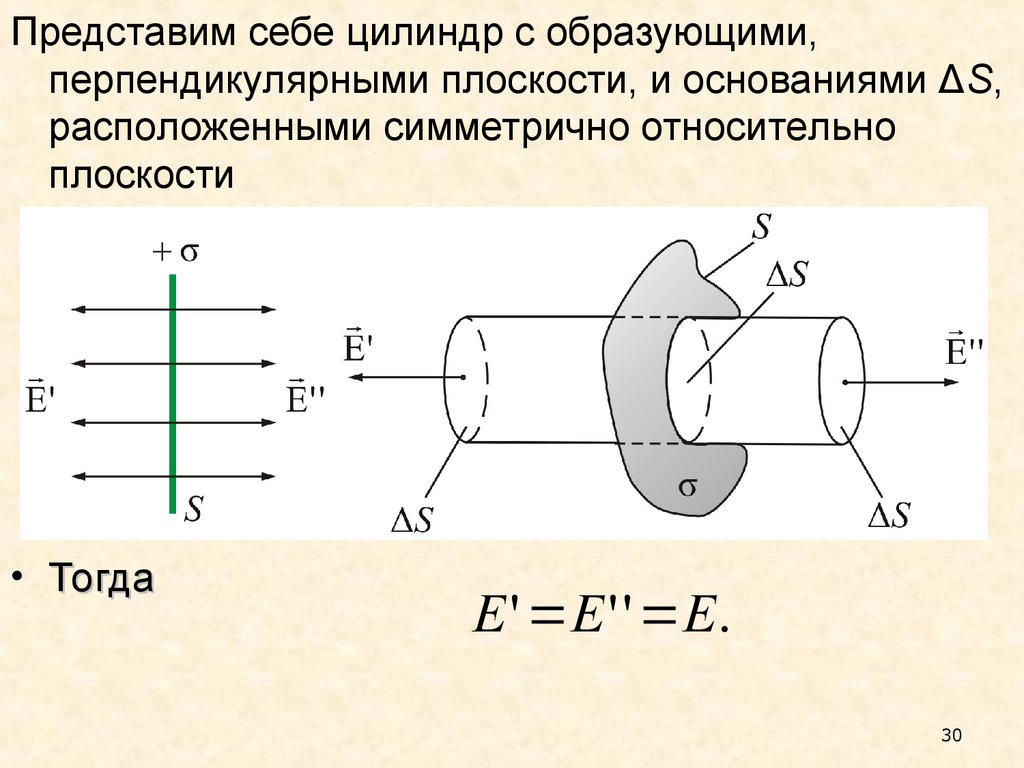
30.
Представим себе цилиндр с образующими,перпендикулярными плоскости, и основаниями ΔS,
расположенными симметрично относительно
плоскости
• Тогда
E ' E ' ' E.
30
31.
Суммарный поток через замкнутую поверхность(цилиндр) будет равен:
ФЕ 2 SE.
• Внутри поверхности заключен заряд.
Следовательно, из теоремы ОстроградскогоГаусса получим:
q
1
ФЕ 2 SE S
0
0
• откуда видно, что напряженность поля
плоскости S :
| |
E
.
2 0
31
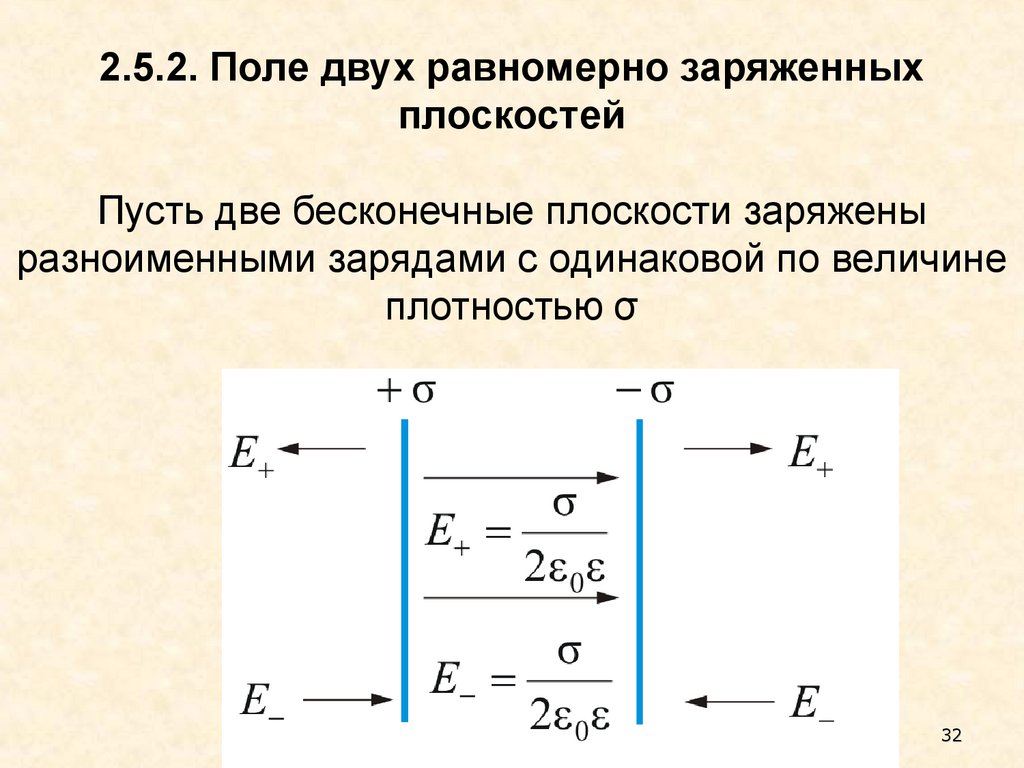
32. 2.5.2. Поле двух равномерно заряженных плоскостей Пусть две бесконечные плоскости заряжены разноименными зарядами с одинаковой
по величинеплотностью σ
32
33.
• Результирующее поле, находится каксуперпозиция полей, создаваемых каждой из
плоскостей.
• Тогда внутри плоскостей
E E E отсюда E / 0
• Вне плоскостей напряженность поля
E 0.
• Полученный результат справедлив и для
плоскостей конечных размеров, если расстояние
между плоскостями гораздо меньше линейных
размеров плоскостей (плоский конденсатор).
33
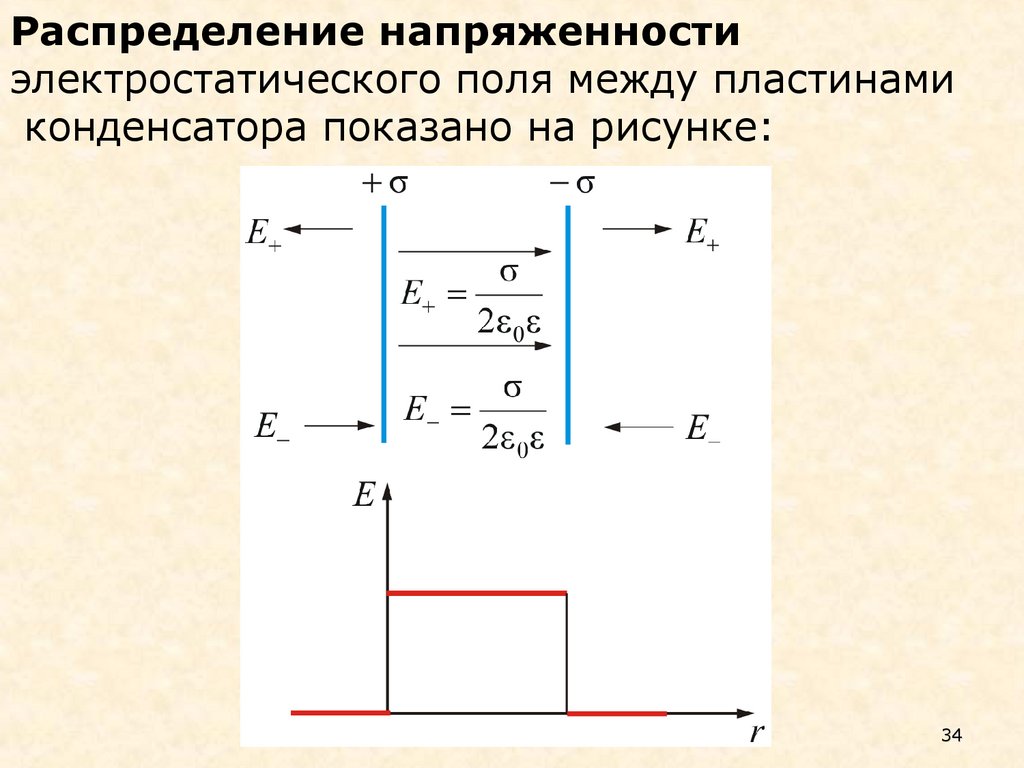
34.
Распределение напряженностиэлектростатического поля между пластинами
конденсатора показано на рисунке:
34
35.
Между пластинами конденсатора действует силавзаимного притяжения (на единицу площади
пластин):
F S E
Fед
S
S
2
Fед
2 0
• Механические силы, действующие между
заряженными телами, называют
пондеромоторными.
35
36.
• Сила притяжения между пластинамиконденсатора:
2
S
F
,
2 0
• где S – площадь обкладок конденсатора.
• Т.к.
q
E 0
S
2
2
0E S
q
F
2 0 S
2
• Это формула для расчета пондеромоторной
силы
36
37.
2.5.3. Поле заряженного бесконечногоцилиндра (нити)
Пусть поле создается бесконечной
цилиндрической поверхностью радиуса R,
заряженной с постоянной линейной
плотностью
dq
dl
• где dq – заряд, сосредоточенный на отрезке
цилиндра
37
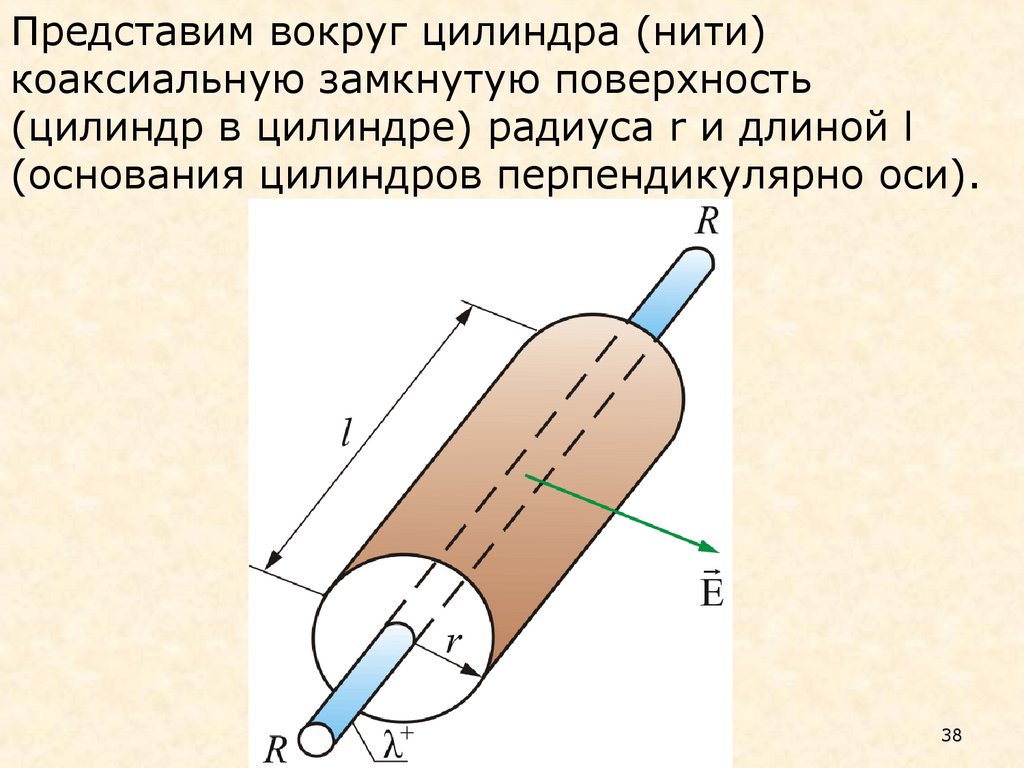
38.
Представим вокруг цилиндра (нити)коаксиальную замкнутую поверхность
(цилиндр в цилиндре) радиуса r и длиной l
(основания цилиндров перпендикулярно оси).
38
39.
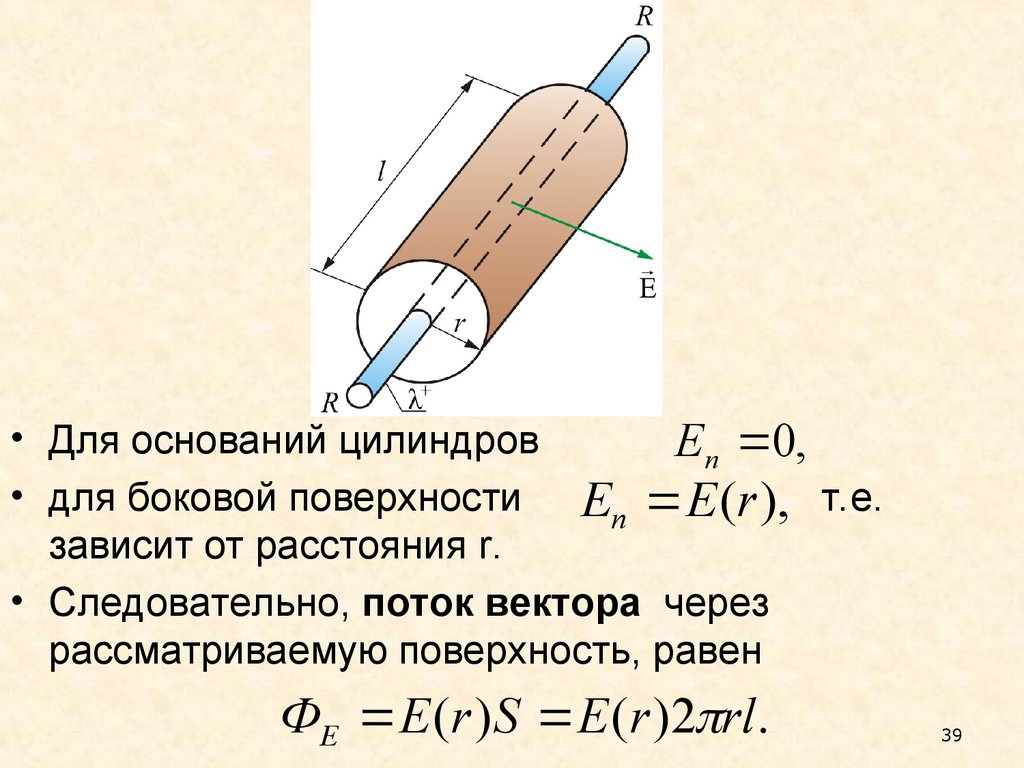
• Для оснований цилиндровEn 0,
• для боковой поверхности E E (r ), т.е.
n
зависит от расстояния r.
• Следовательно, поток вектора через
рассматриваемую поверхность, равен
ФE E (r ) S E (r )2 rl.
39
40.
• Приr R, на поверхности будет заряд q l.
• По теореме Остроградского-Гаусса
• Тогда
Е (r )
при r R
2 0 r
l
E (r )2 rl
0
• Если r R, E ( r ) 0 , т.к. внутри замкнутой
поверхности зарядов нет.
40
41.
• График распределениянапряженности
электростатического
поля цилиндра
0 внутри цилиндра, так как внутри нет зарядов
q
E
или
на поверхности цилиндра
2 0 Rl
2 0 R
q
или
вне цилиндра
2 0 rl
2 0 r
41
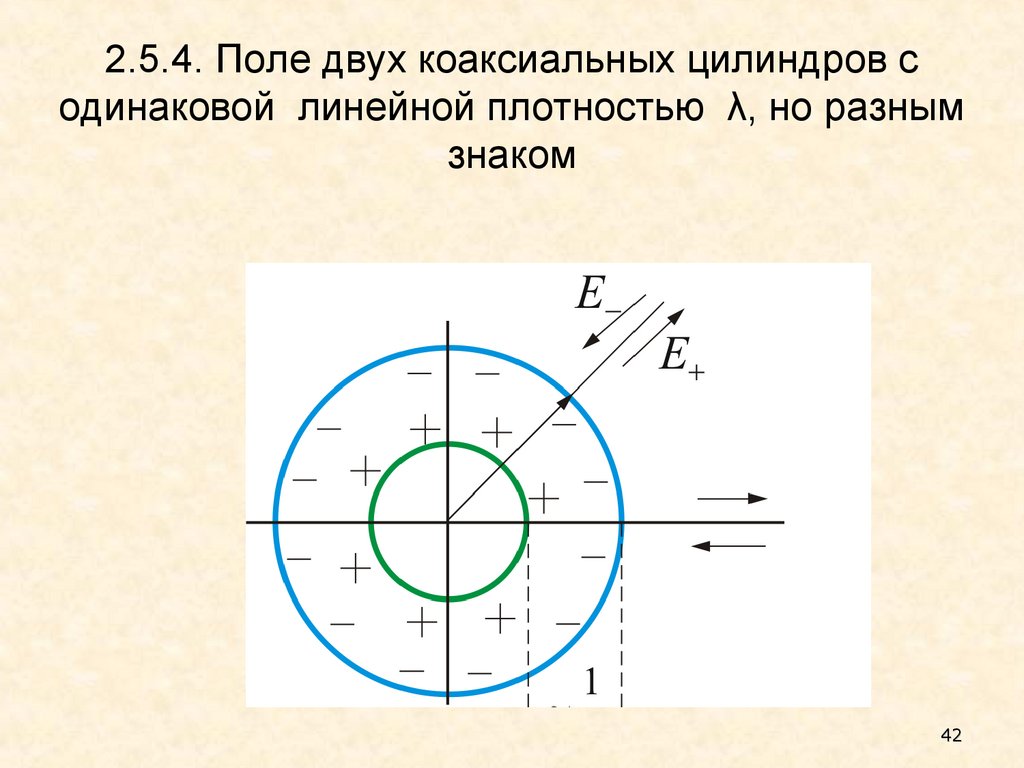
42. 2.5.4. Поле двух коаксиальных цилиндров с одинаковой линейной плотностью λ, но разным знаком
E 042
43.
Внутри меньшего и вне большего цилиндровполе будет отсутствовать
E 0
В зазоре между цилиндрами, поле
определяется:
E (r )
.
2 0 r
43
44. Таким образом для коаксиальных цилиндров имеем:
0 внутри меньшего и вне большего цилиндров зарядов нетE
2 r между цилиндрами, когда R1 r R2
0
• Это справедливо и для бесконечно длинного
цилиндра, и для цилиндров конечной длины, если
зазор между цилиндрами намного меньше длины
цилиндров (цилиндрический конденсатор).
44
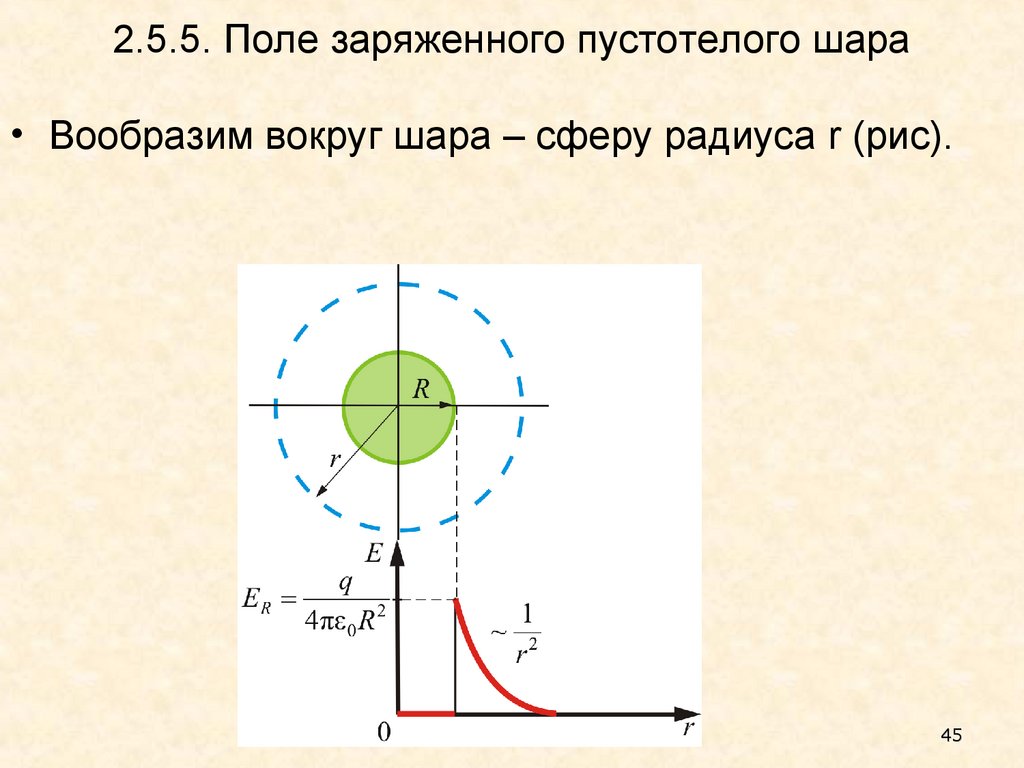
45. 2.5.5. Поле заряженного пустотелого шара
• Вообразим вокруг шара – сферу радиуса r (рис).45
46.
• Если r R, то внутрь воображаемой сферыпопадет весь заряд q, распределенный по сфере,
тогда
q
ФE E (r ) S Е (r )4 r
0
2
• откуда поле вне сферы:
q
E (r )
.
2
4 0 r
• Внутри сферы, при r R, поле будет равно
нулю, т.к. там нет зарядов:
E (r ) 0.
Вне сферы поле тождественно полю
точечного заряда той же величины,
помещенному в центр сферы.
46
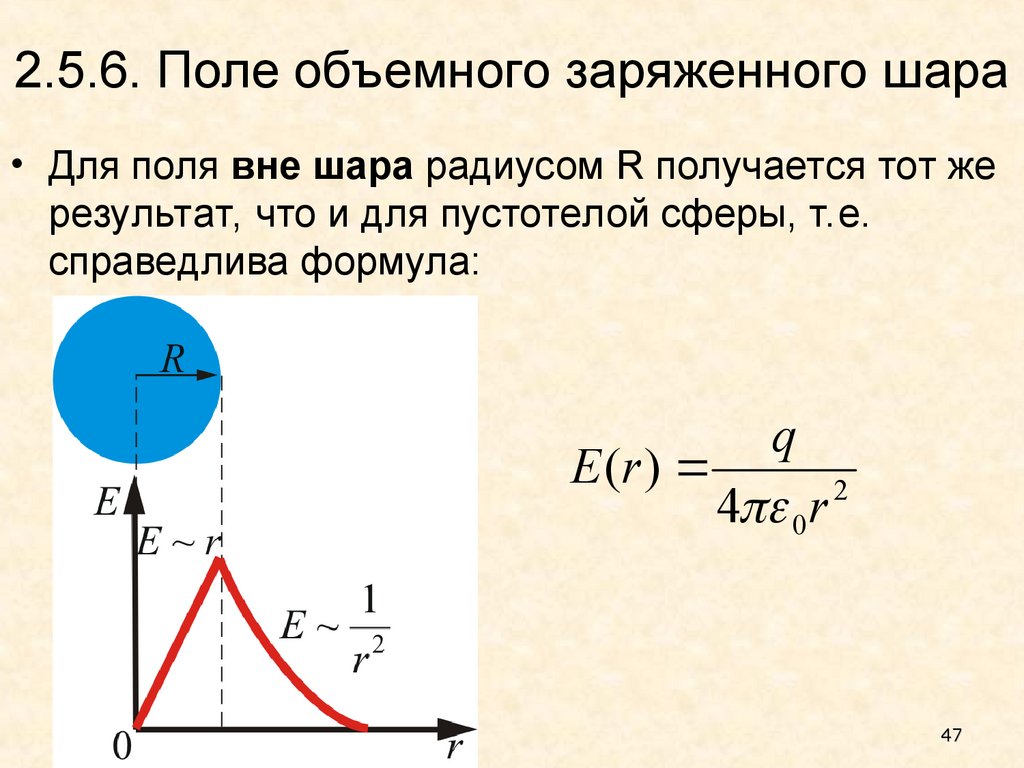
47. 2.5.6. Поле объемного заряженного шара
• Для поля вне шара радиусом R получается тот жерезультат, что и для пустотелой сферы, т.е.
справедлива формула:
q
E (r )
2
4 0 r
47
48.
• Внутри шара при r R, сферическаяповерхность будет содержать в себе заряд,
равный
4 3
q r ,
3
• где ρ – объемная плотность заряда:
объем шара:
4
V r 3
3
q
V
• Тогда, по теореме Остроградского-Гаусса:
1 4 3
Ô E E (r ) S Å (r ) 4 r r
0 3
2
48
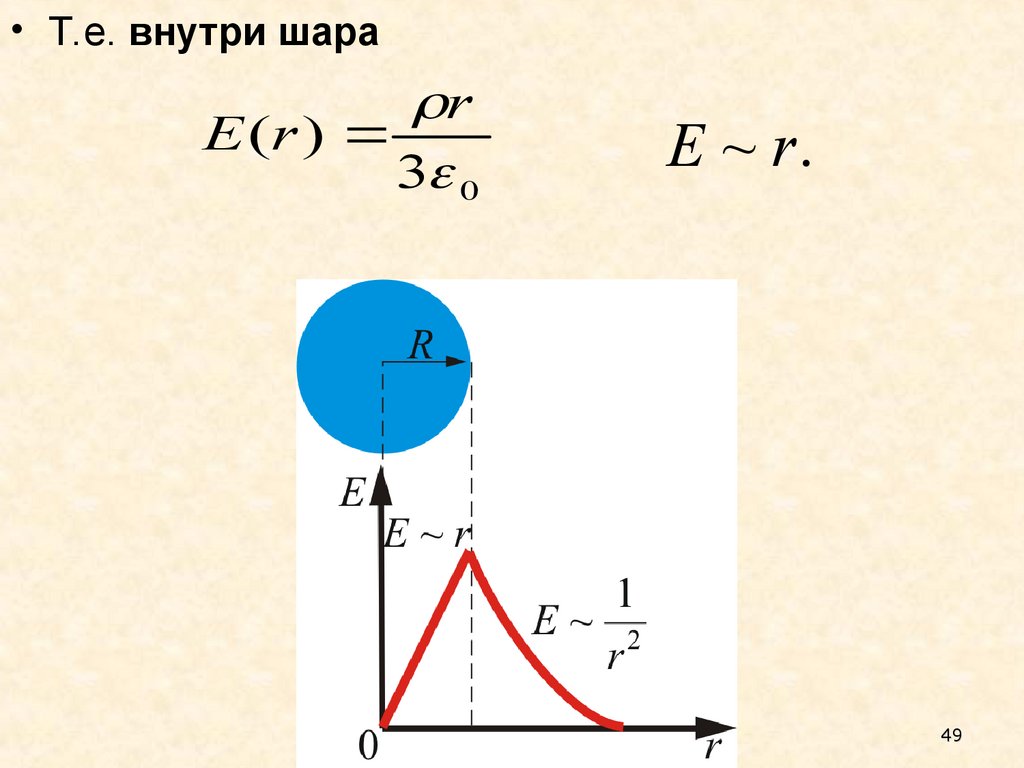
49.
• Т.е. внутри шараr
E (r )
3 0
E ~ r.
49
50. Таким образом, имеем: поле объемного заряженного шара
qrr
внутри шара (r R)
3
3 0
4 0 R
q
E
на поверхности шара (r R)
2
4 0 R
q
вне шара (r R)
2
4 0 r
50
































 Физика
Физика








