Похожие презентации:
Теорема Остроградского-Гаусса
1.
Лекция 3.ТЕОРЕМА ОСТРОГРАДСКОГО-ГАУССА
3.1. Силовые линии электростатического поля
3.2. Поток вектора напряженности
3.3. Теорема Остроградского-Гаусса
3.4. Дифференциальная форма теоремы Остроградского-Гаусса
3.5. Вычисление электростатических полей с помощью
теоремы Остроградского - Гаусса
3.5.1. Поле бесконечной однородно заряженной
плоскости
3.5.2. Поле двух равномерно заряженных плоскостей
3.5.3. Поле заряженного бесконечного цилиндра (нити)
3.5.4. Поле двух коаксиальных цилиндров с одинаковой
линейной плотностью заряда, но разным знаком
3.5.5. Поле заряженного пустотелого шара
3.5.6. Поле объемного заряженного шара
2. 3.1. Силовые линии электростатического поля
Теорема Остроградского-Гаусса, которую мыдокажем и обсудим позже, устанавливает связь
между электрическими зарядами и электрическим
полем. Она представляет собой более общую и
более изящную формулировку закона Кулона.
3.
Основная ценность теоремыОстроградского-Гаусса состоит в том, что
она позволяет глубже понять природу
электростатического поля и
устанавливает более общую связь
между зарядом и полем.
4.
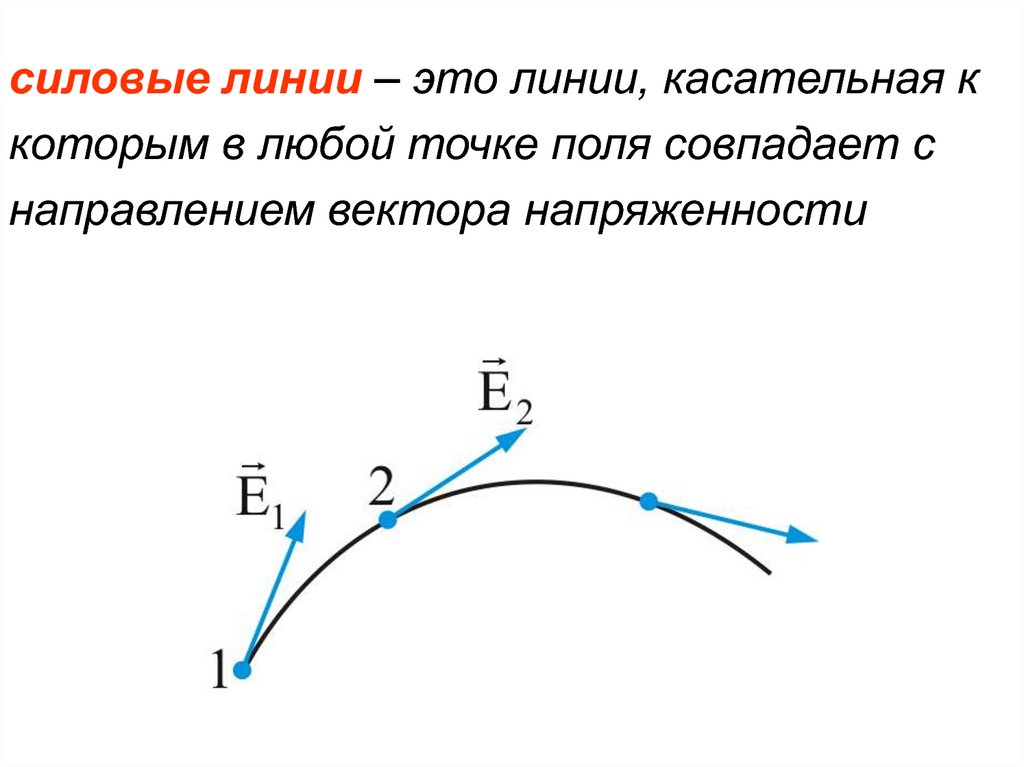
силовые линии – это линии, касательная ккоторым в любой точке поля совпадает с
направлением вектора напряженности
5.
Однородным называется электростатическоеполе, во всех точках которого напряженность
одинакова по величине и направлению, т.е.
однородное электростатическое поле
изображается параллельными силовыми линиями
на равном расстоянии друг от друга
E
6.
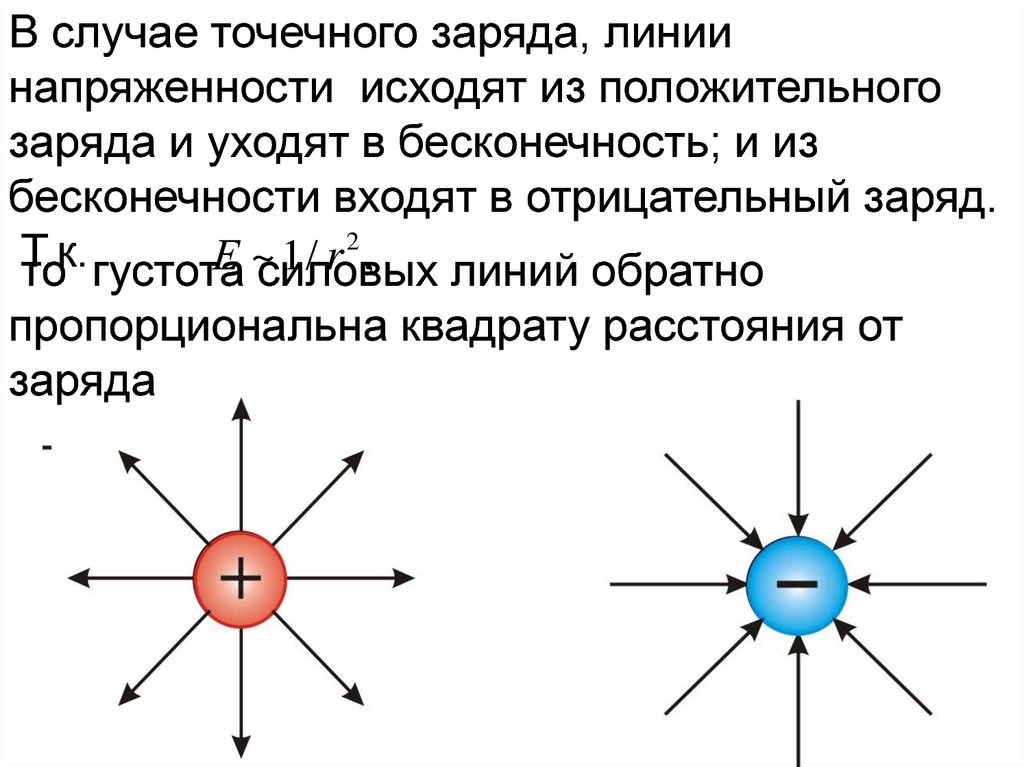
В случае точечного заряда, линиинапряженности исходят из положительного
заряда и уходят в бесконечность; и из
бесконечности входят в отрицательный заряд.
2
Т.к.
Е
~
1
/
r
,
то густота силовых
линий обратно
пропорциональна квадрату расстояния от
заряда
7.
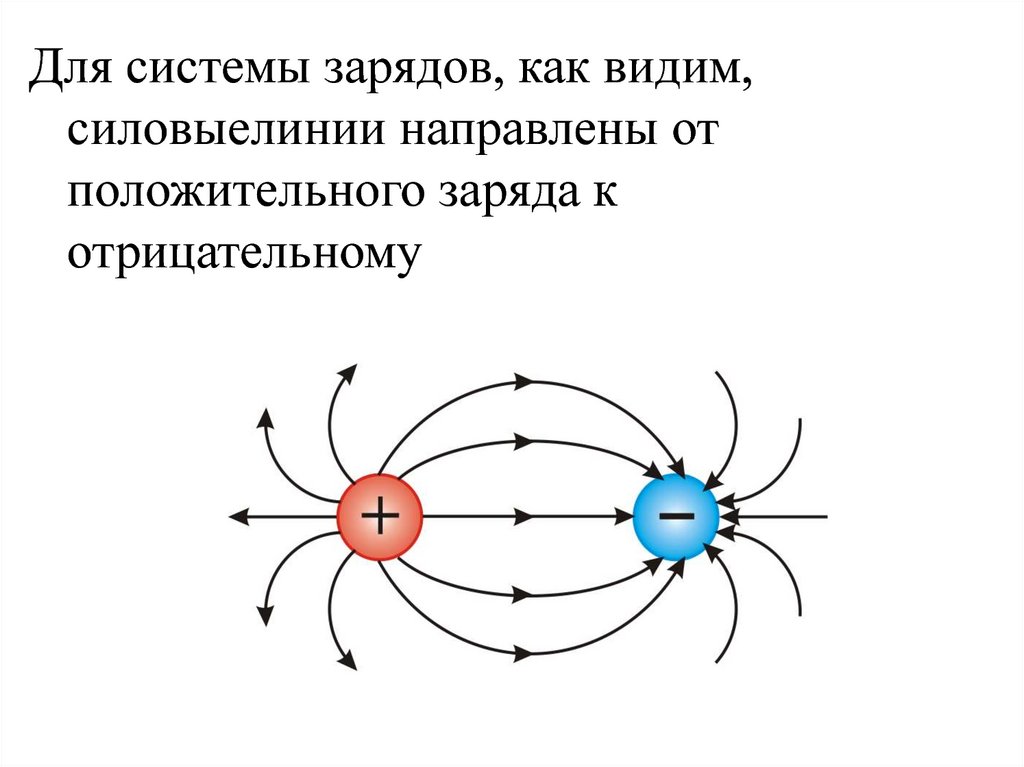
Для системы зарядов, как видим,силовыелинии направлены от
положительного заряда к
отрицательному
8.
9.
Густота силовых линий должна быть такой,чтобы единичную площадку, нормальную к
вектору напряженности пересекало такое
их число, которое равно модулю вектора
напряженности Е , т.е.
число линий Ф
Е
.
S
S
10.
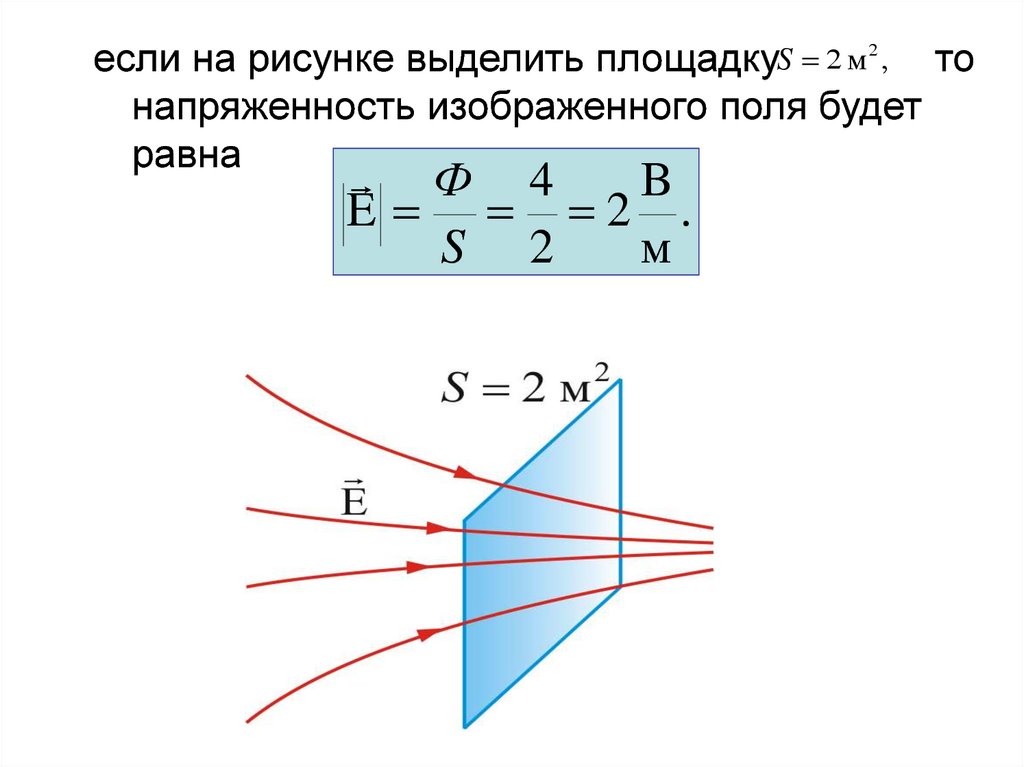
если на рисунке выделить площадкуS 2 м 2 , тонапряженность изображенного поля будет
равна
Ф 4
B
E 2 .
S 2
м
11.
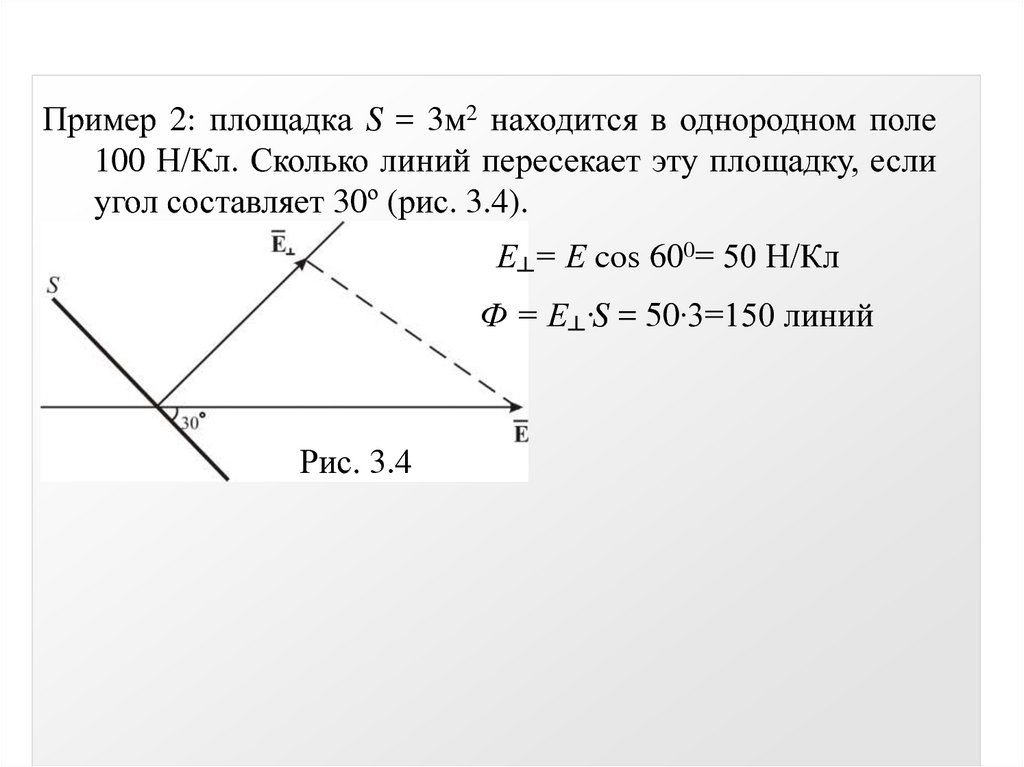
Пример 2: площадка S = 3м2 находится в однородном поле100 Н/Кл. Сколько линий пересекает эту площадку, если
угол составляет 30º (рис. 3.4).
Е┴= Е cos 600= 50 Н/Кл
Ф = Е┴·S = 50·3=150 линий
Рис. 3.4
12.
3.2. Поток векторанапряженности
Итак, на примерах мы показали, что если силовые
линии
однородного
электрического
поля
напряженностью
E
пронизывают некоторую площадку S, то поток напряженности
(раньше мы называли число силовых линий через площадку)
будет определяться формулой
ФE ES ES cos α E
S
n
(3.1)
E
где En – произведение вектора
на нормаль n к данной площадке
(рис. 3.5).
А величина ФЕ здесь и называется
потоком вектора напряженности
электрического
поля
через
площадку S, т.е. определение:
Рис. 3.5.
13.
Полное число силовых линий, проходящихчерез поверхность S называется потоком
вектора напряженности ФЕ через эту
поверхность.
ФЕ (Е, S)
В векторной форме можно записать
S (3.2)
nS
– скалярное произведение двух векторов, где вектор
Таким образом, поток вектора есть скаляр,
который в зависимости от величины угла α
может быть как положительным, так и
отрицательным.
.
14.
15.
Для первого рисунка – поверхность А1 окружаетположительный заряд и поток здесь направлен
наружу, т.е. ФE 0.
Поверхность А2 – окружает отрицательный заряд,
здесь
поток
внутрь и
ФЕнаправлен
0
Общий поток через поверхность А равен нулю.
Опишите второй рисунок самостоятельно.
16. 3.3. Теорема Остроградского-Гаусса
3.3. Теорема ОстроградскогоГауссаИтак, по определению, поток вектора
напряженности электрического поля равен
числу линий напряженности, пересекающих
поверхность S.
17.
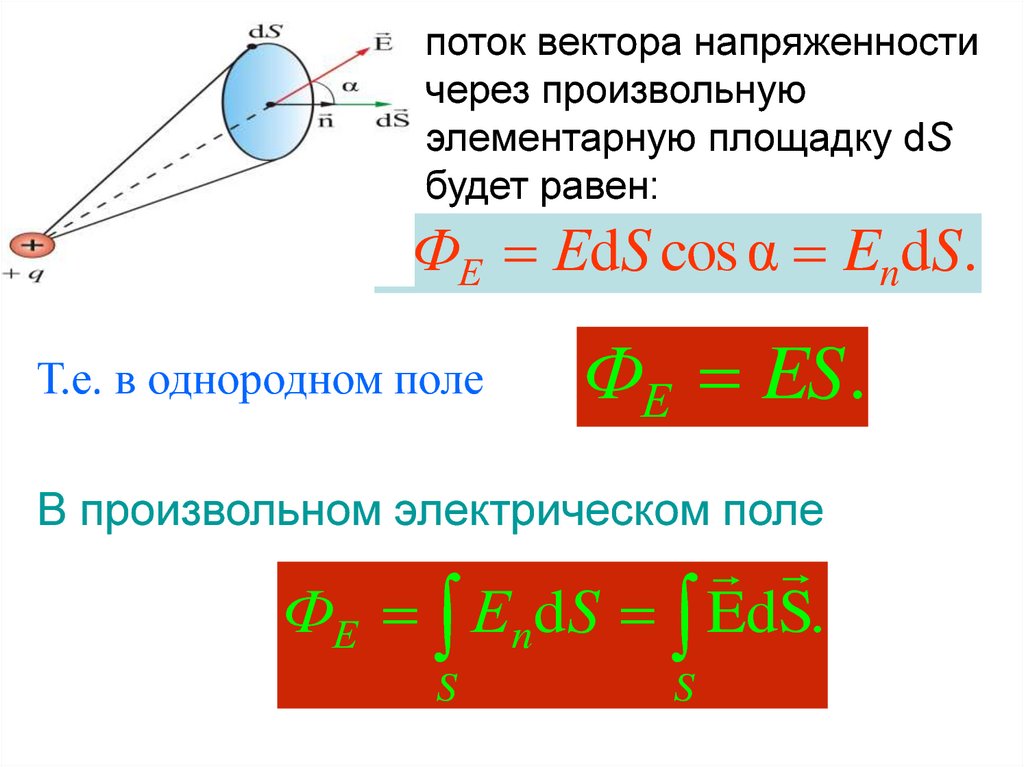
поток вектора напряженностичерез произвольную
элементарную площадку dS
будет равен:
dФЕ ЕdS cos α EndS .
Т.е. в однородном поле
ФЕ ES .
В произвольном электрическом поле
ФЕ ЕndS EdS.
S
S
18.
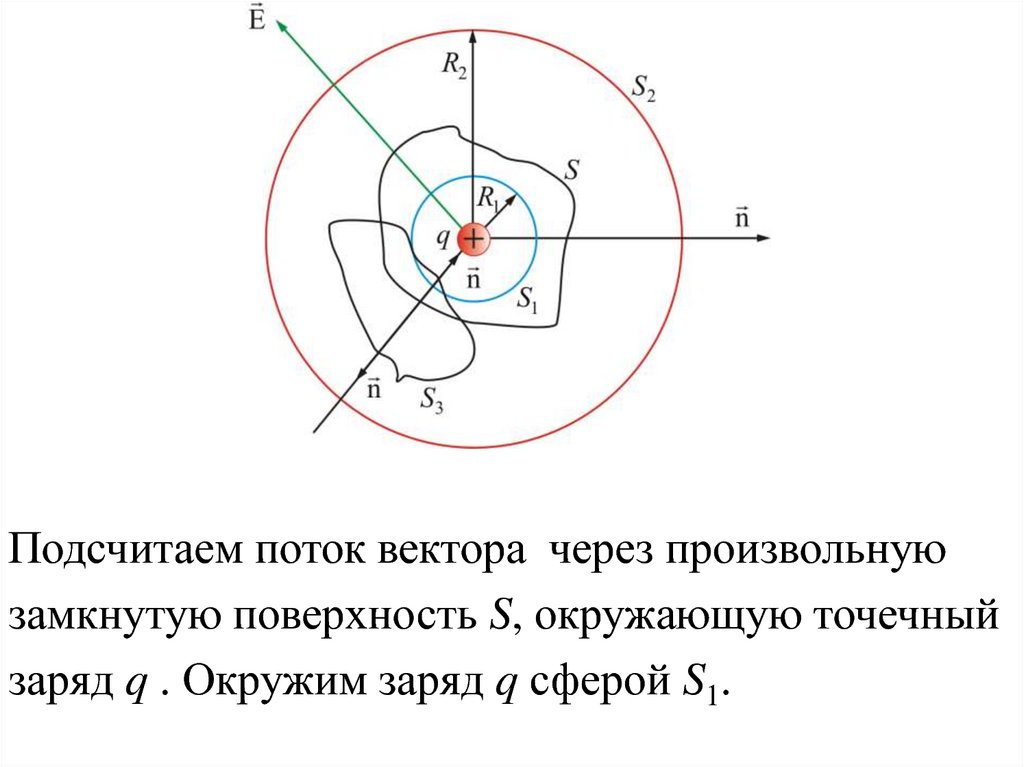
Подсчитаем поток вектора через произвольнуюзамкнутую поверхность S, окружающую точечный
заряд q . Окружим заряд q сферой S1.
19.
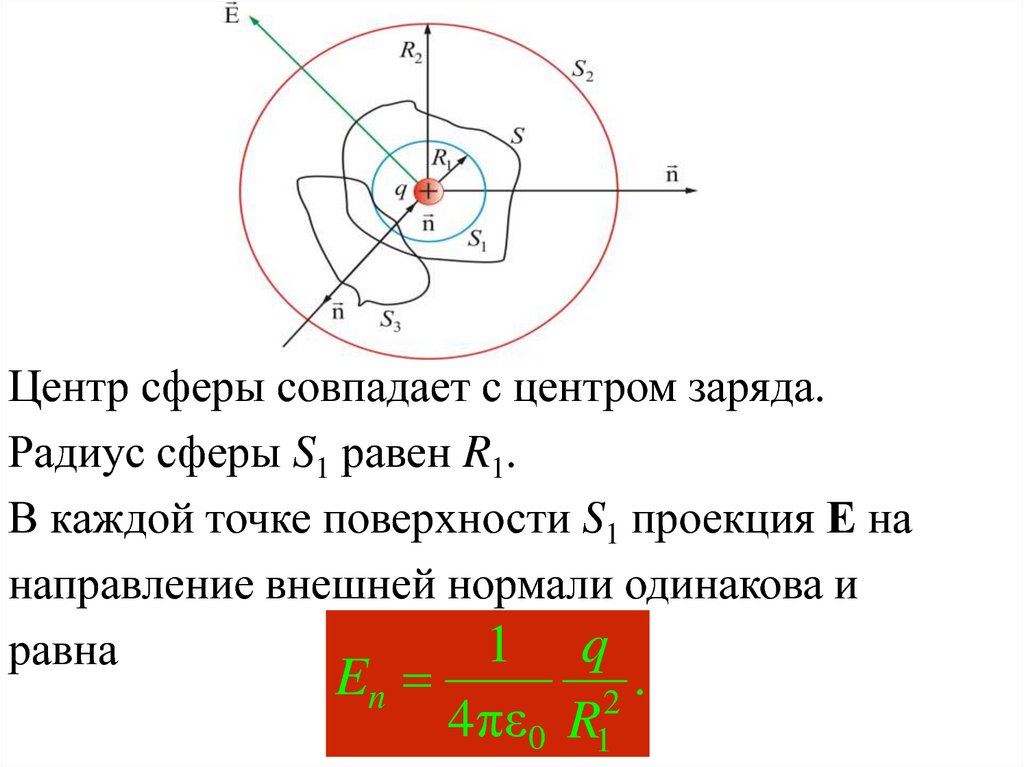
Центр сферы совпадает с центром заряда.Радиус сферы S1 равен R1.
В каждой точке поверхности S1 проекция Е на
направление внешней нормали одинакова и
1 q
равна
En
.
2
4πε0 R1
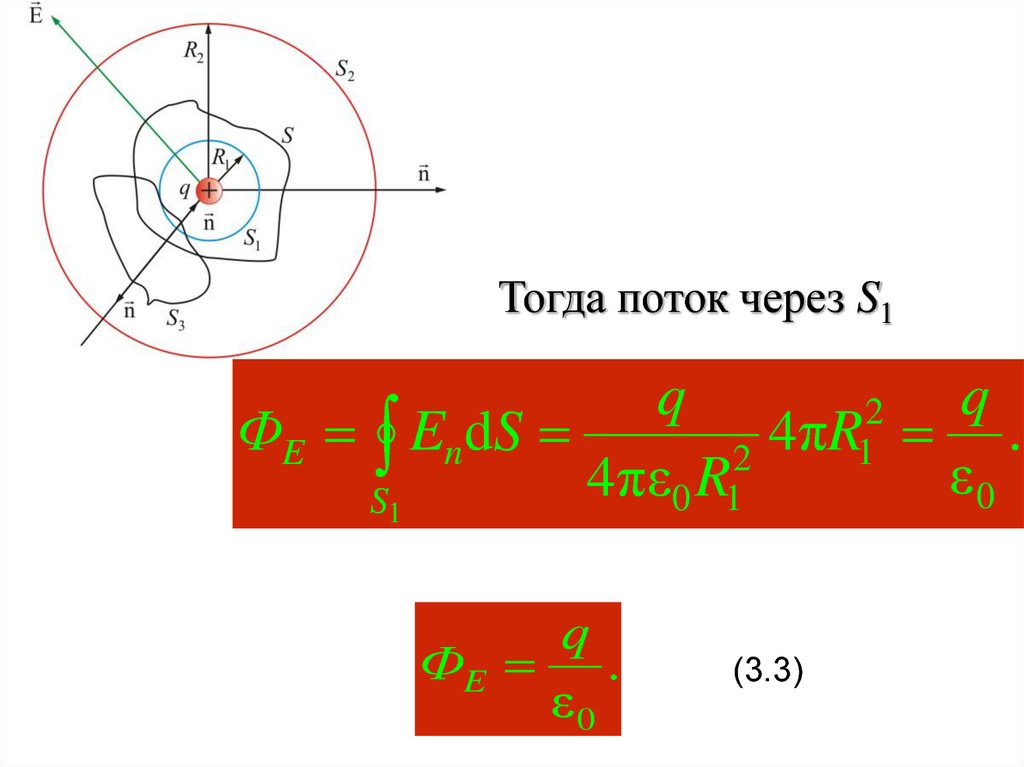
20.
Тогда поток через S1q
q
2
ФE En dS
4πR1 .
2
ε
4
πε
R
0
0
1
S1
q
ФE .
ε0
(3.3)
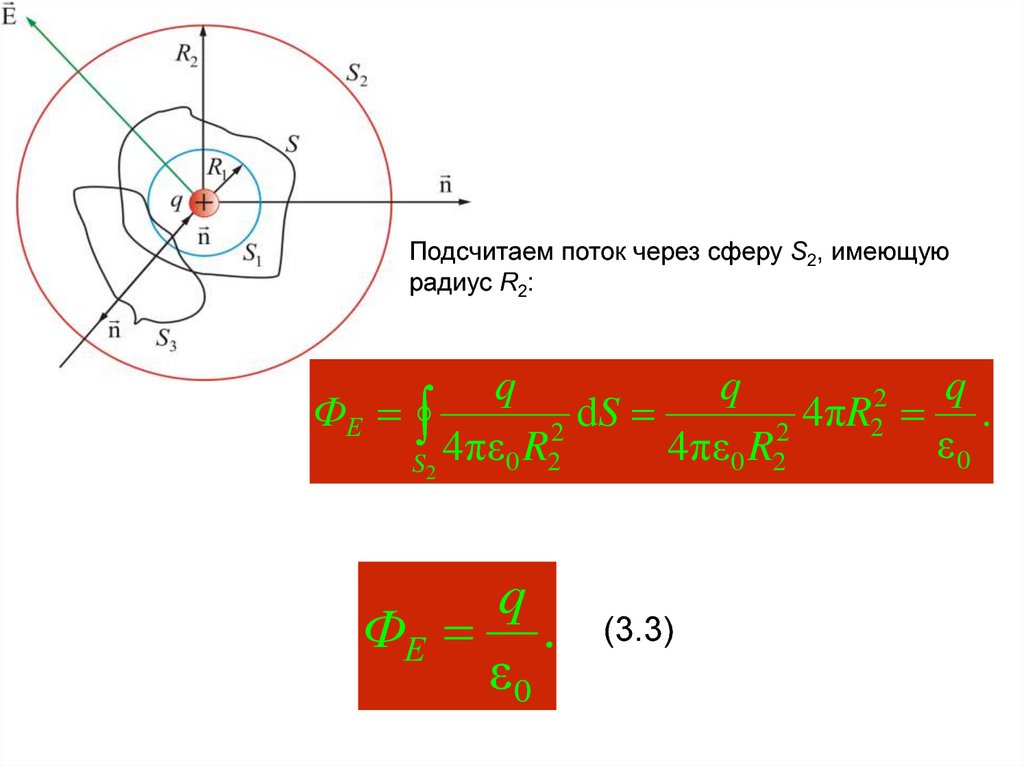
21.
Подсчитаем поток через сферу S2, имеющуюрадиус R2:
q
q
q
2
ФЕ
dS
4πR2 .
2
2
ε0
4πε0 R2
S2 4 πε 0 R2
q
ФЕ .
ε0
(3.3)
22.
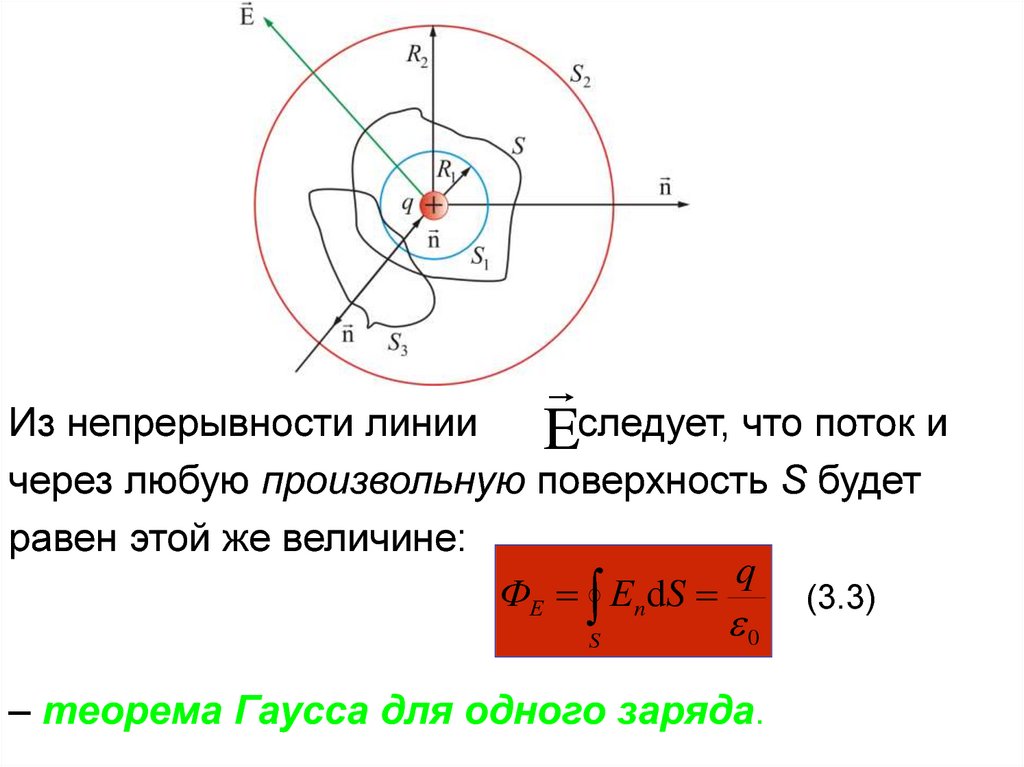
Eследует, что поток иИз непрерывности линии
через любую произвольную поверхность S будет
равен этой же величине:
q
ФЕ Еn dS
(3.3)
0
S
– теорема Гаусса для одного заряда.
23.
Длялюбого
числа
расположенных
зарядов,
внутри поверхности:
ФЕ
S
q
Е dS
n
0
произвольно
находящихся
(3.4)
– теорема Гаусса для нескольких
зарядов.
Поток вектора напряженности
электрического поля через замкнутую
поверхность в вакууме равен алгебраической
сумме всех зарядов, расположенных внутри
поверхности, деленной на ε0.
24.
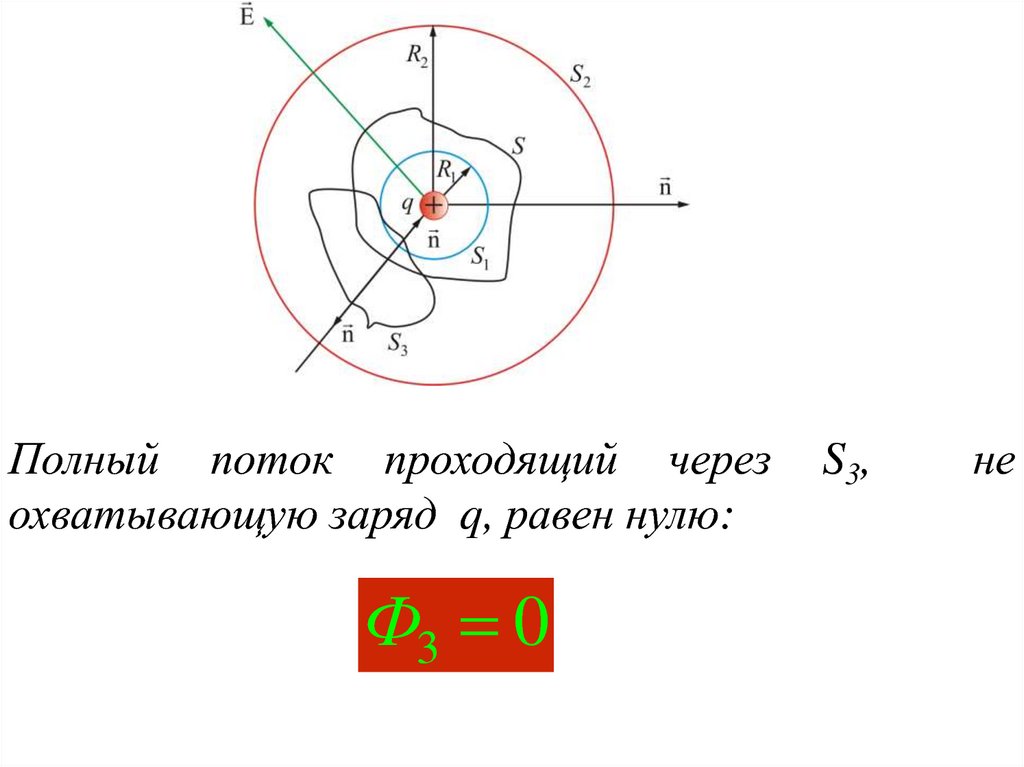
Полный поток проходящий черезохватывающую заряд q, равен нулю:
Ф3 0
S 3,
не
25.
Таким образом, для точечного заряда q,полный поток через любую замкнутую
поверхность S будет равен:
ФЕ
q
0 – если заряд расположен внутри
замкнутой поверхности;
ФЕ 0
– если заряд расположен вне
замкнутой поверхности;
этот результат не зависит от формы
поверхности, и знак потока совпадает со
знаком заряда.
26.
Электрические заряды могут быть «размазаны» снекоторой объемной плотностью, различной в
разных местах пространства:
ρ dq / dV
Здесь dV – физически бесконечно малый объем,
под которым следует понимать такой объем,
который с одной стороны достаточно мал,
чтобы в пределах его плотность заряда
считать одинаковой, а с другой – достаточно
велик, чтобы не могла проявиться
дискретность заряда, т.е. то, что любой заряд
кратен целому числу элементарных зарядов
электрона или протона .
27.
Суммарный заряд объема dV будет равен:qi ρdV .
V
Тогда из теоремы Гаусса можно получить:
1
ФE ЕdS ρdV
ε
0V
S
1
ФE ρdV
ε0 V
(3.5)
это ещё одна форма записи теоремы
Остроградского-Гаусса, если заряд
неравномерно распределен по объему.
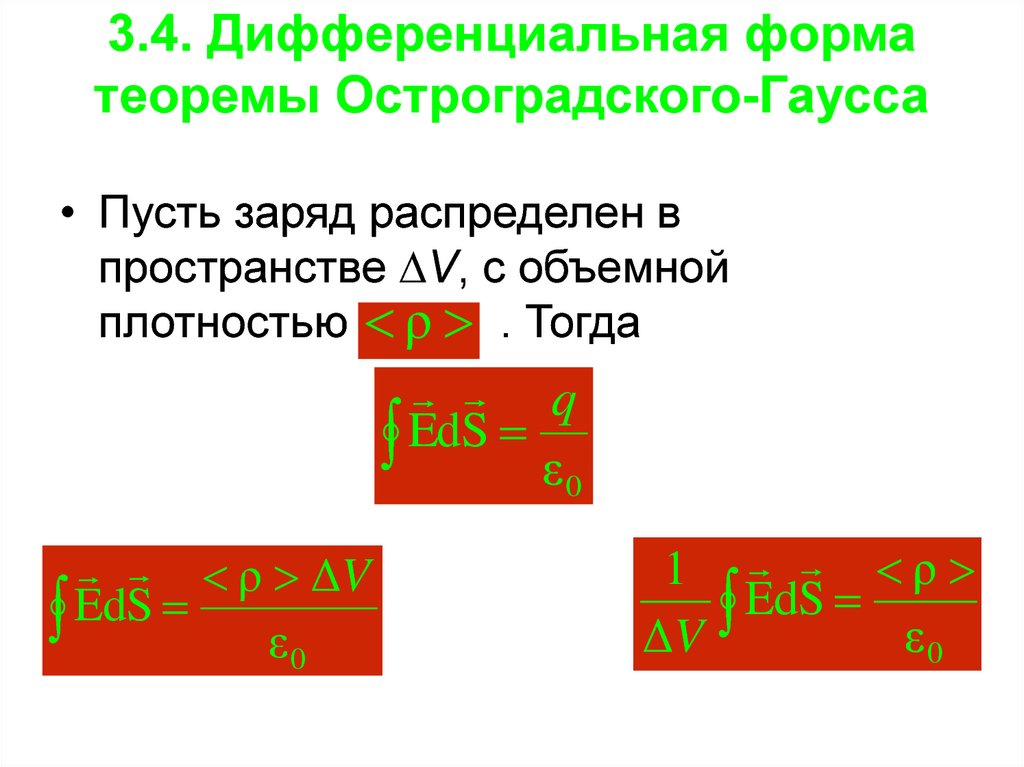
28. 3.4. Дифференциальная форма теоремы Остроградского-Гаусса
• Пусть заряд распределен впространстве V, с объемной
плотностью ρ . Тогда
q
EdS ε 0
ρ ΔV
EdS ε 0
1 ρ
EdS
ΔV
ε0
29.
Теперь устремим ΔV 0 , стягивая его кинтересующей нас точке. Очевидно, что при
этом ρ будет стремиться к ρ в данной точке,
т.е.
ρ
ρ
ε0
ε0
.
Величину, являющуюся пределом отношения ЕdS
к V, при ΔV 0 ,
называют дивергенцией поля Е и обозначаютя
.
div E
30.
Дивергенция поля Е1
div E lim
EdS.
V 0 V
(3.6)
Аналогично определяется дивергенция любого другого
векторного поля.
Из этого определения следует, что дивергенция является
скалярной функцией координат.
В декартовой системе координат
Ex E y Ez
div E
.
x
y
z
31.
Итак,ρ
div E .
ε0
(3.6.а)
Это теорема Остроградского-Гаусса в
дифференциальной форме.
Написание многих формул упрощается, если
ввести векторный
дифференциальный
оператор (Набла)
i j k,
x y z
где i, j, k – орты осей
(единичные векторы).
32.
Сам по себе оператор смысла не имеет. Онприобретает смысл в сочетании с векторной или
скалярной функцией, на которую символично
умножается:
E x E y E z
Е x Ex y E y z Ez
x
y
z
дифференциальная форма теоремы
Остроградского-Гаусса.
E
0
(3.6.б)
33.
В тех точках поля, где div E 0–
источники поля (положительные заряды),
где div E
заряды).
0
– стоки (отрицательные
Линии выходят из источников и
заканчиваются в стоках.




















 Физика
Физика








