Похожие презентации:
Введение. Точка. Прямая. Начертательная геометрия и инженерная графика. Лекция № 1
1.
Начертательная геометрия иинженерная графика
• Лектор:
ст. преподаватель Томского политехнического
университета отделения общетехнических дисциплин.
Романова Светлана Владимировна
• e-mail: romanova@tpu.ru
1
2. Лекция № 1
ВведениеТочка
Прямая
Лекция № 1
2
3.
ВведениеНачертательная
геометрия
Инженерная графика
(Черчение)
3
4.
Начертательнаягеометриянаука о
проекционных
изображениях
4
5.
Начертательная геометриярассматривает:
•Методы изображения
пространственных фигур
на плоскости
• Свойства фигур по их
изображениям
5
6.
В черчении изучаютсяправила выполнения
и чтения чертежей
отдельных деталей
и сборочных единиц
6
7.
ЛитератураВинокурова Г.Ф.,Степанов Б.Л.,
Инженерная графика
Учебное пособие.Томск: Изд. ТПУ
А.А. Чекмарев Инженерная графика
В.С. Левицкий Машиностроительное
черчение и автоматизация выполнения
чертежей
7
8.
Историческаясправка
Основоположник
начертательной
геометрии Гаспар Монж
8
9.
ГаспарМонж
(1746 -1818)
9
10.
Первый учебникпо начертательной
геометрии
опубликован
во Франции
в 1798 г.
10
11.
В 1810 г. Карл Потьеначал читать лекции по
начертательной геометрии
в Петербургском Институте
корпуса инженеров
путей сообщения
11
12.
В 1821г. в Россиииздан первый учебник по
начертательной геометрии
на русском языке
профессора
Я.А.Севастьянова
12
13.
ВалентинНиколаевич
Джонс
28(16)октября 1900г.
прочел в ТТИ
первую лекцию
по начертательной
геометрии
13
14.
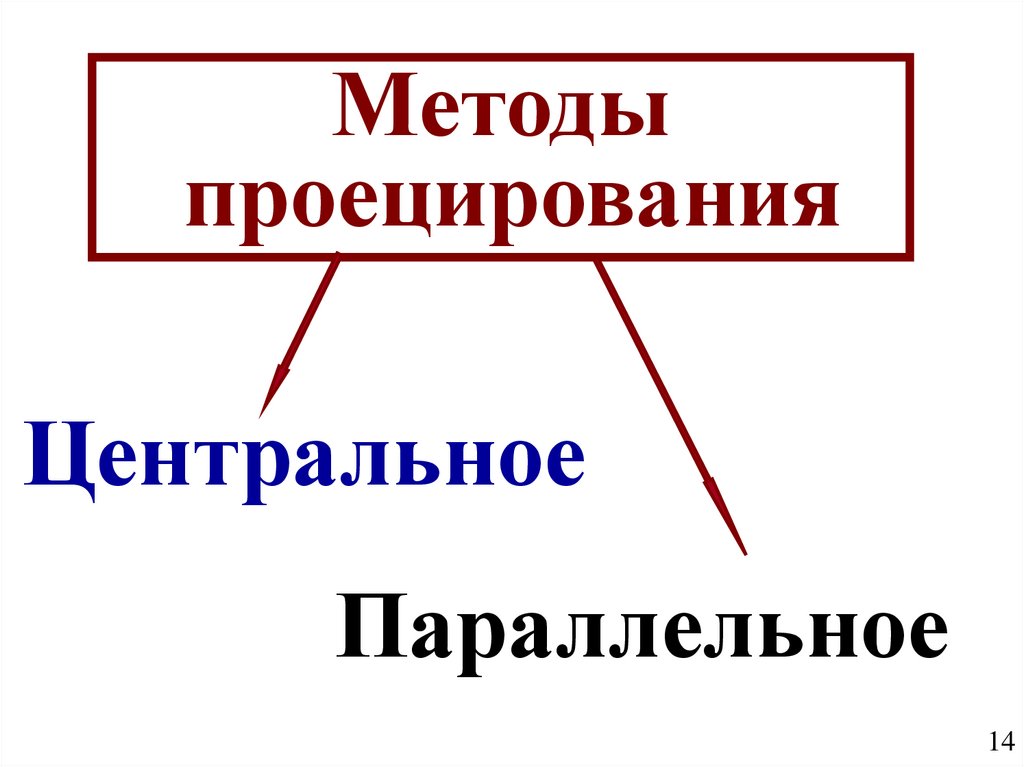
Методыпроецирования
Центральное
Параллельное
14
15.
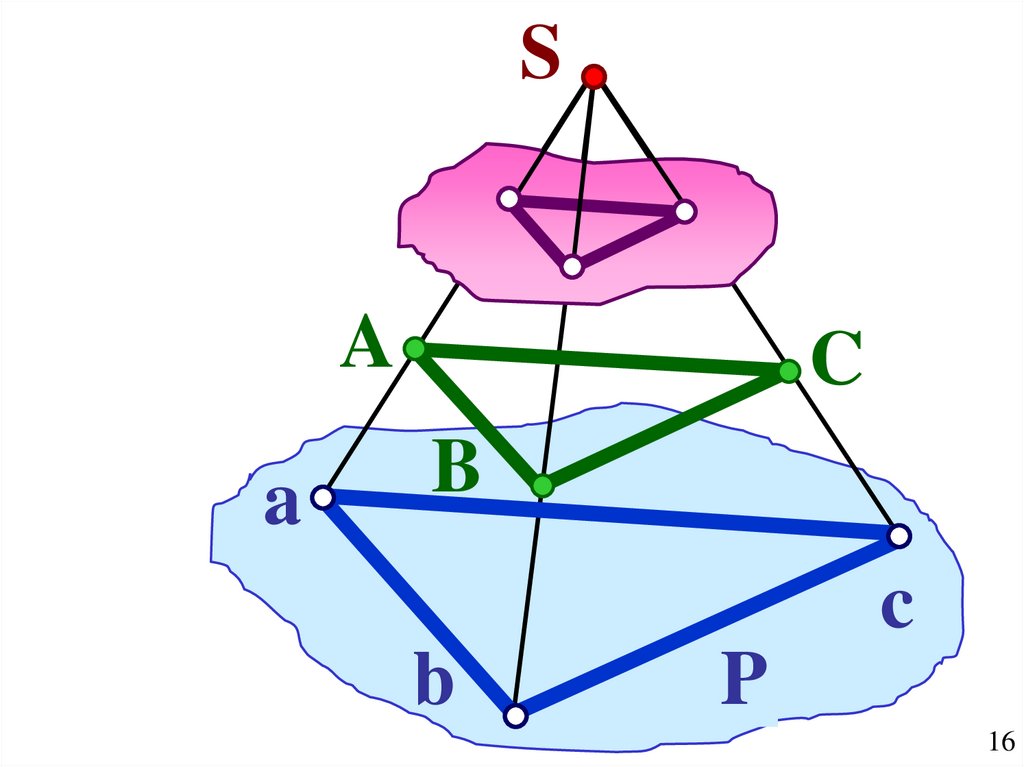
Центральное Sпроецирование
A
a
C
B
c
b
P
15
16.
SA
a
C
B
c
b
P
16
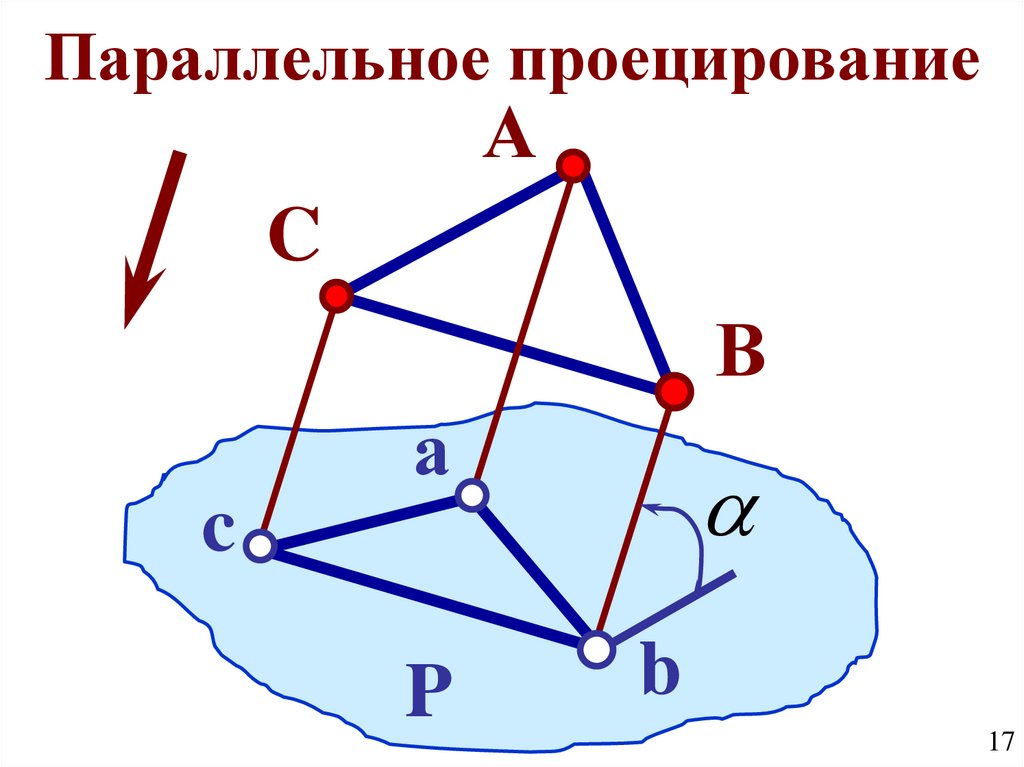
17.
Параллельное проецированиеА
C
В
а
c
P
b
17
18. - косоугольное проецирование
90 - прямоугольноепроецирование
90 - косоугольное
проецирование
18
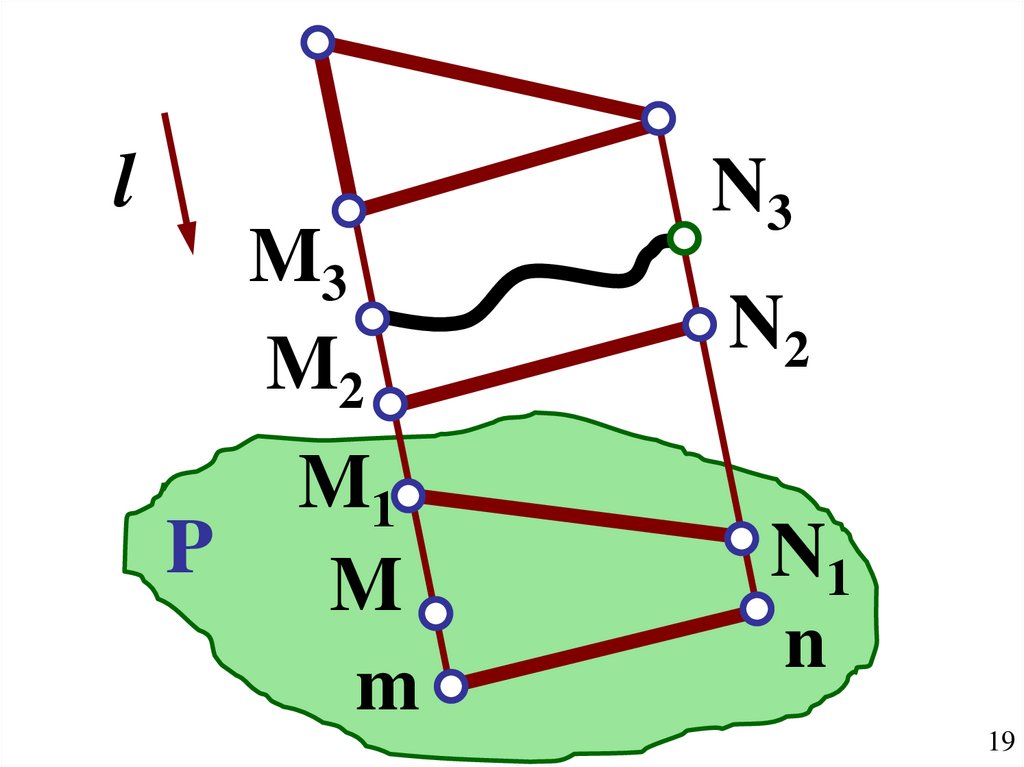
19.
lM3
M2
P
M1
M
m
N3
N2
N1
n
19
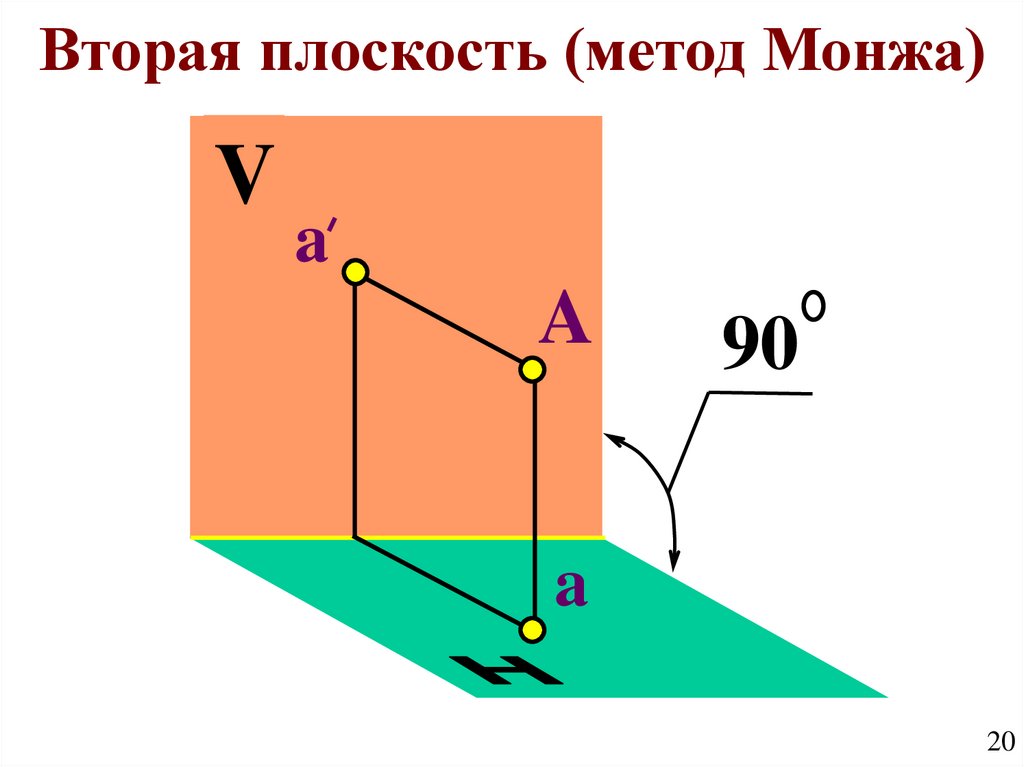
20.
Вторая плоскость (метод Монжа)V
a
A
90
a
20
21.
V21
22.
V22
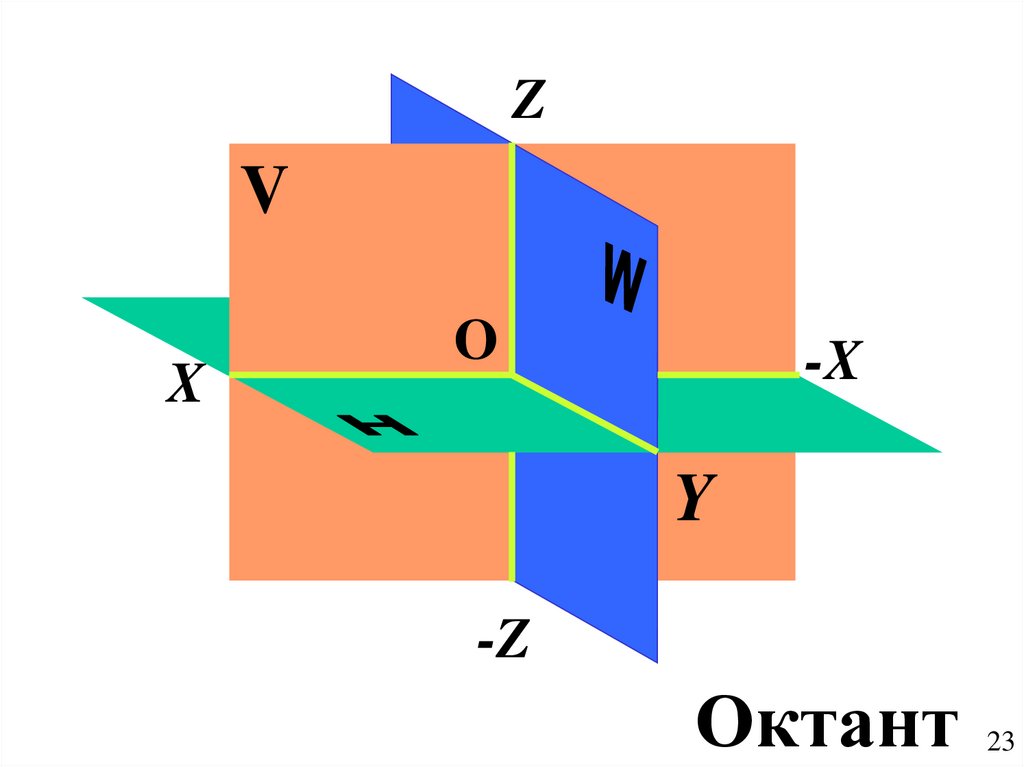
23.
ZV
X
O
-X
Y
-Z
Октант
23
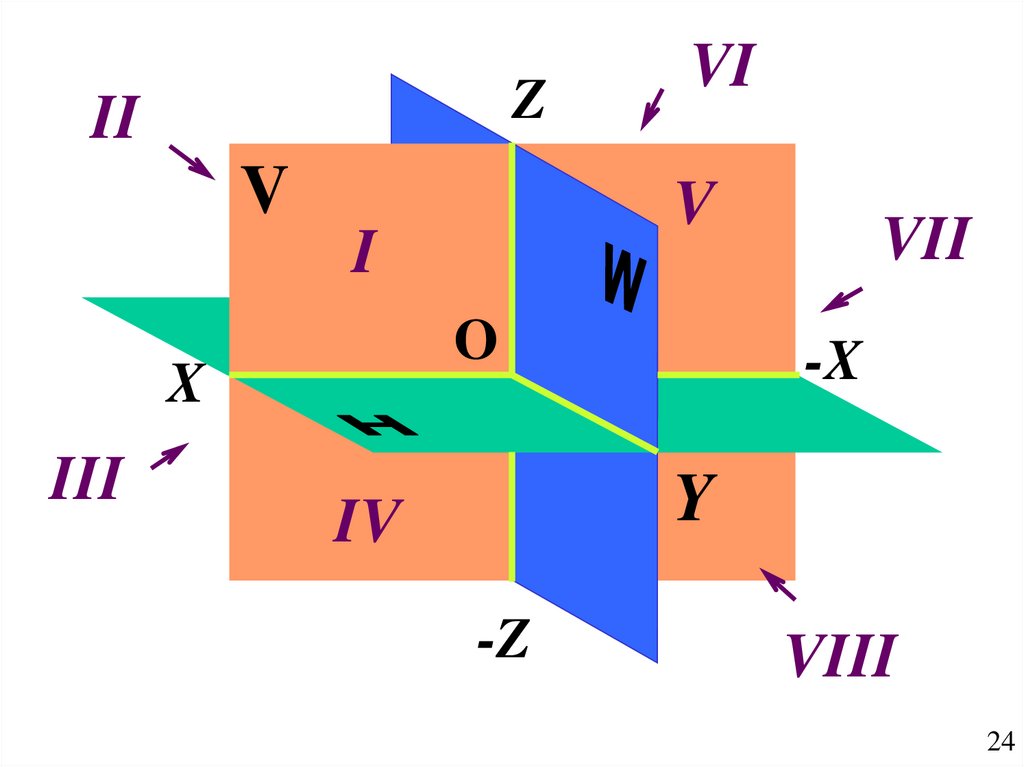
24.
ZII
V
V
I
O
X
III
VI
VII
-X
Y
IV
-Z
VIII
24
25. Точка
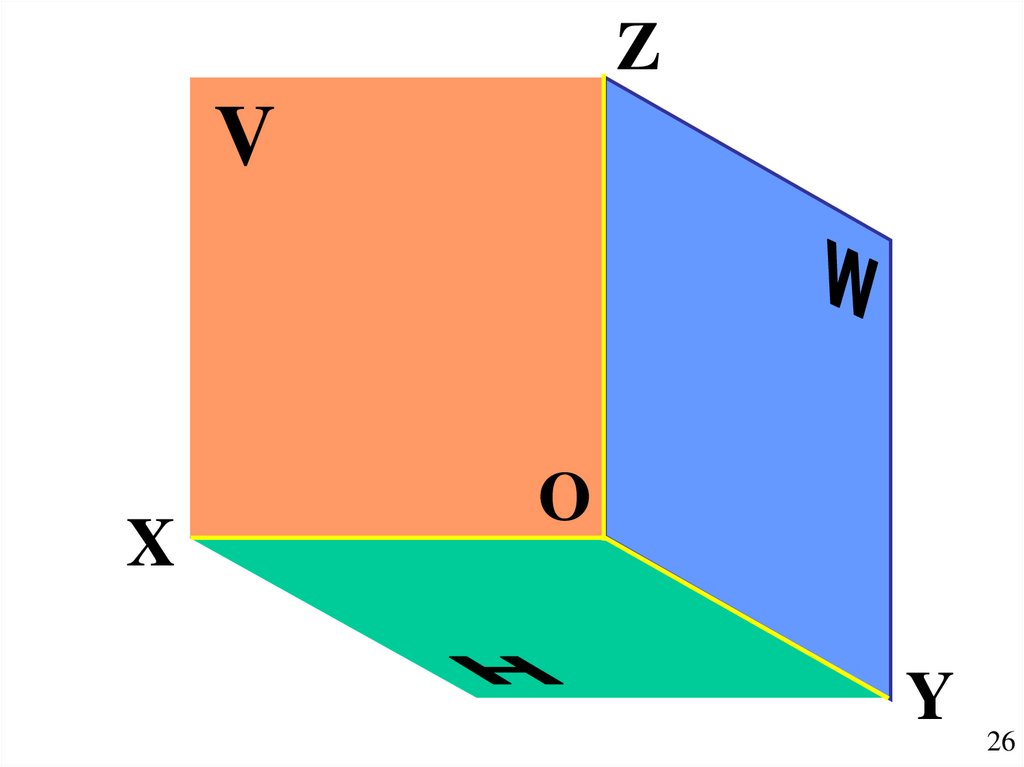
2526.
ZV
X
O
Y
26
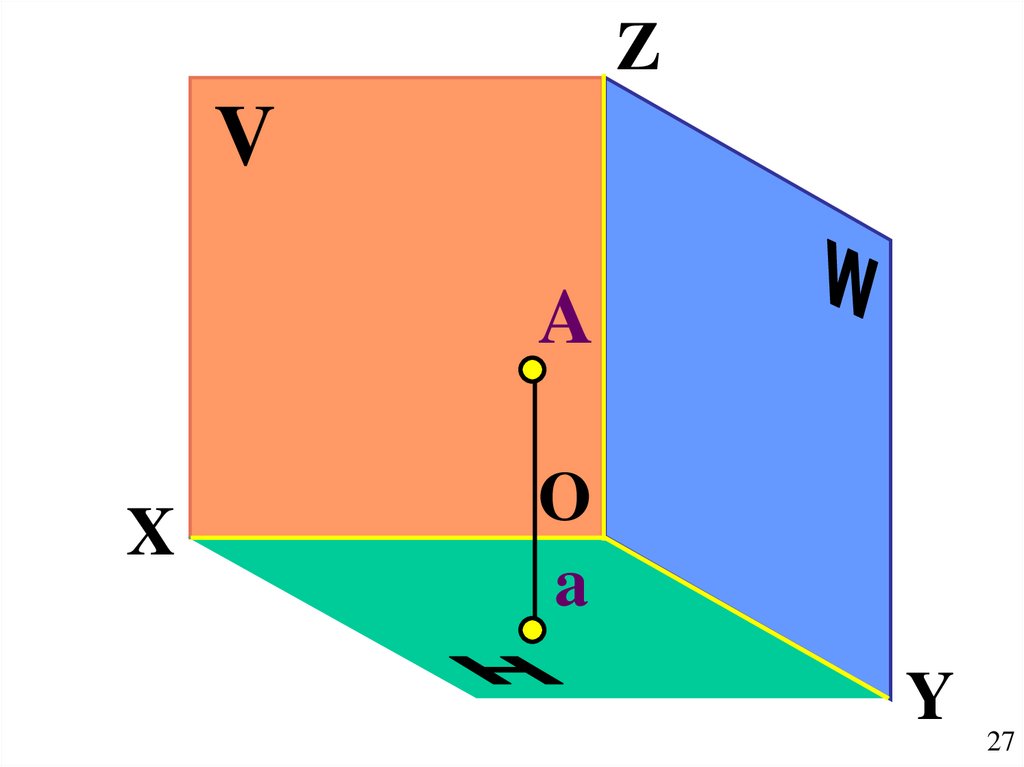
27.
ZV
A
X
O
a
Y
27
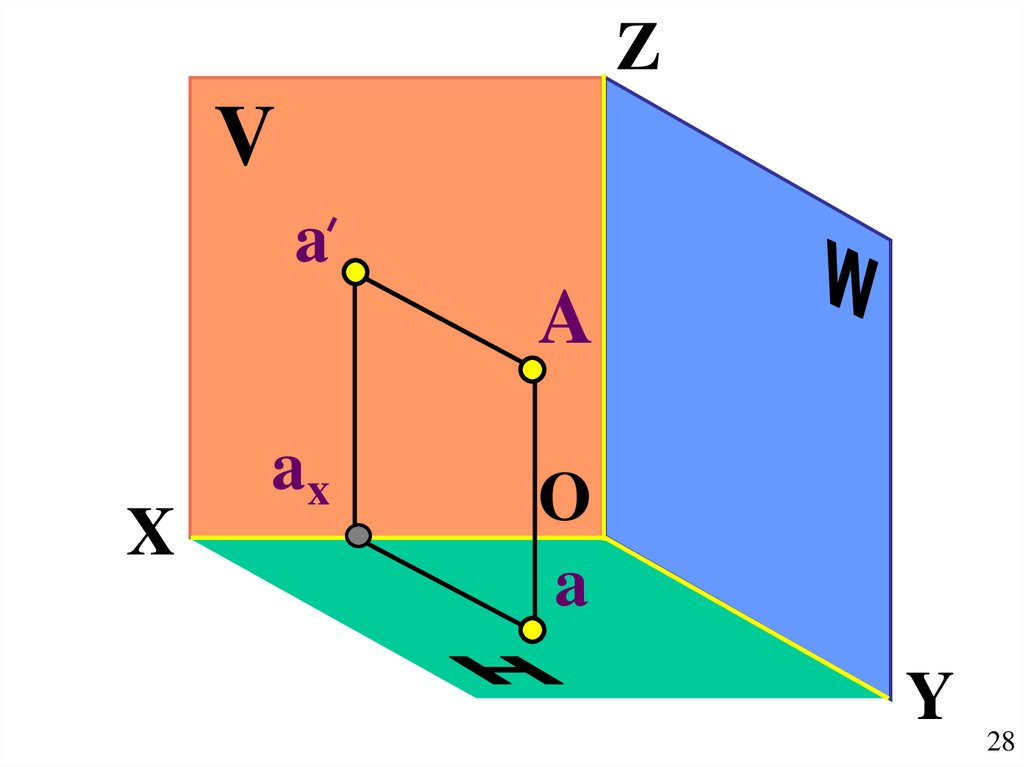
28.
ZV
a
A
X
ax
O
a
Y
28
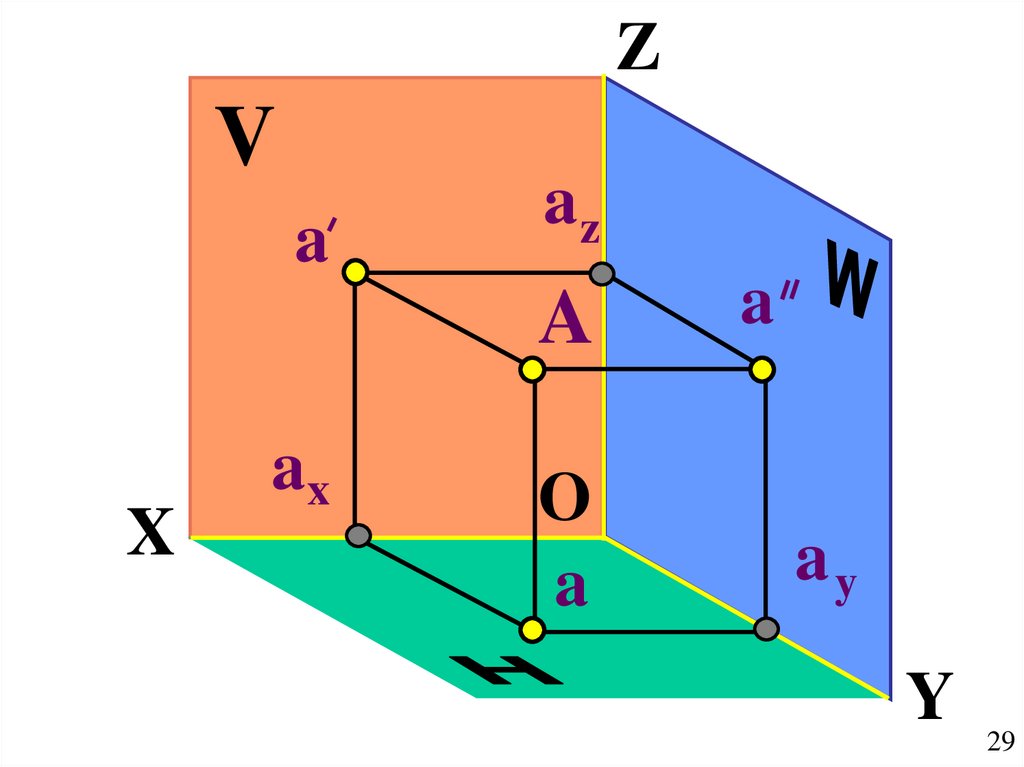
29.
ZV
a
az
A
X
ax
O
a
a
ay
Y
29
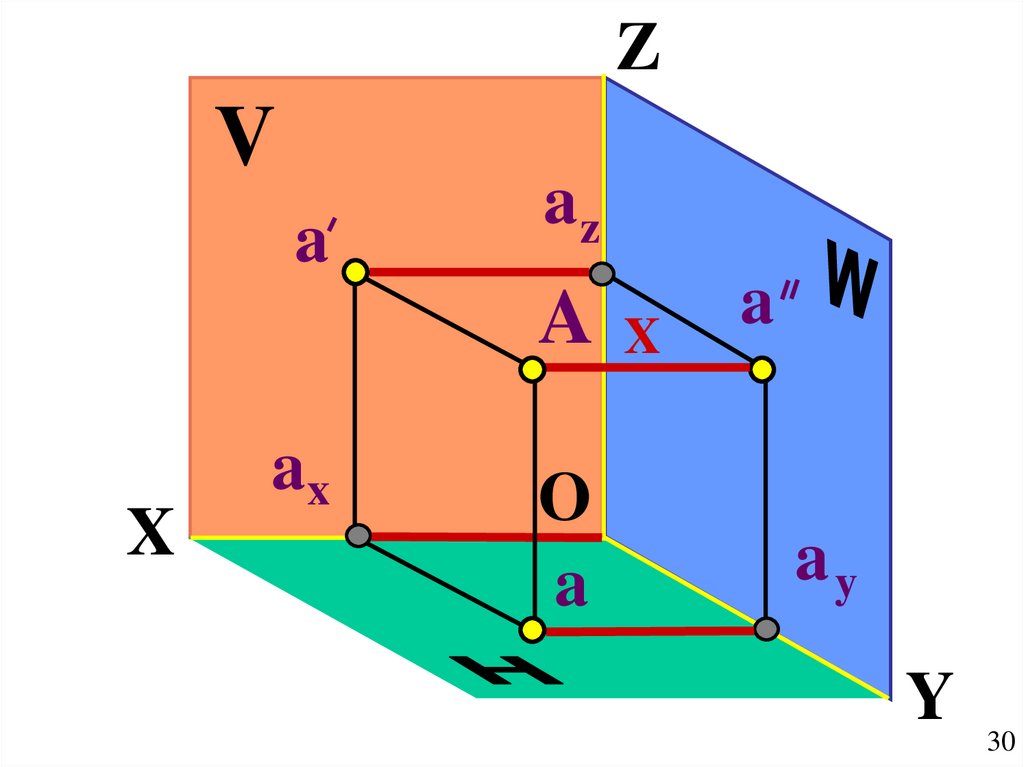
30.
ZV
a
az
A
X
ax
O
a
X
a
ay
Y
30
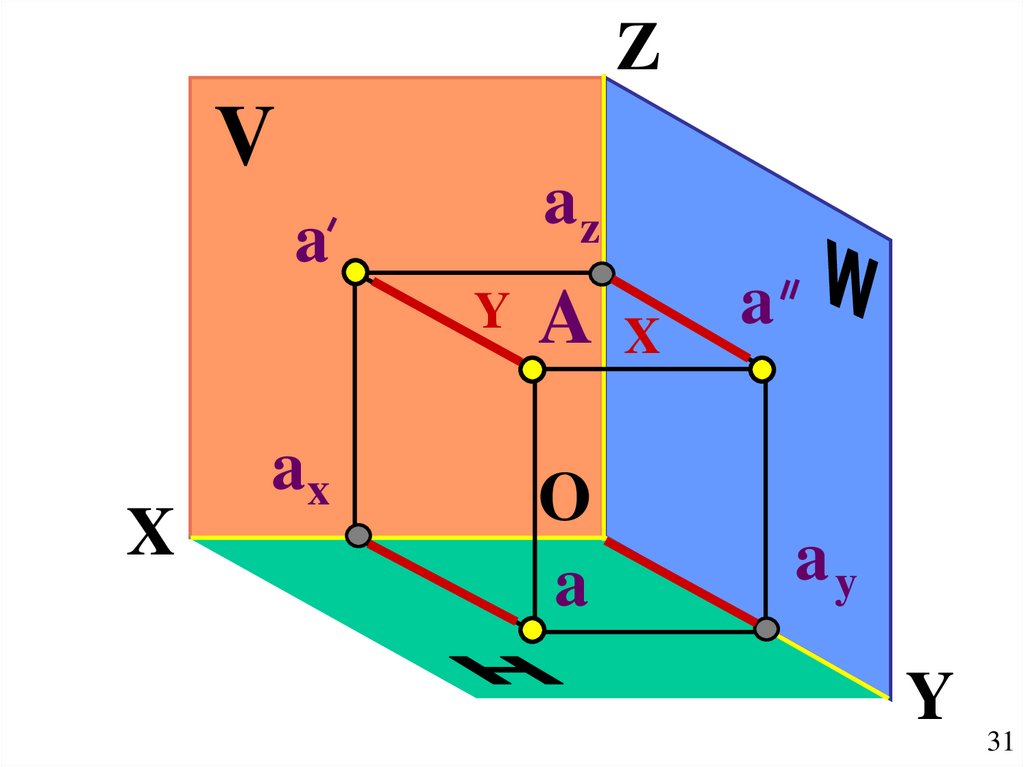
31.
ZV
az
a
Y
X
ax
A
O
a
X
a
ay
Y
31
32.
ZV
az
a
Y
X
ax
A
O
a
X
a
ay
Y
32
33.
ZV
az
a
Y
X
ax
A
O
a
X
a
ay
Y
33
34.
ZV
az
a
X
ax
Y
A
Z
O
a
X
a
ay
Y
34
35.
ZV
az
a
X
ax
Y
A
Z
O
a
X
a
ay
Y
35
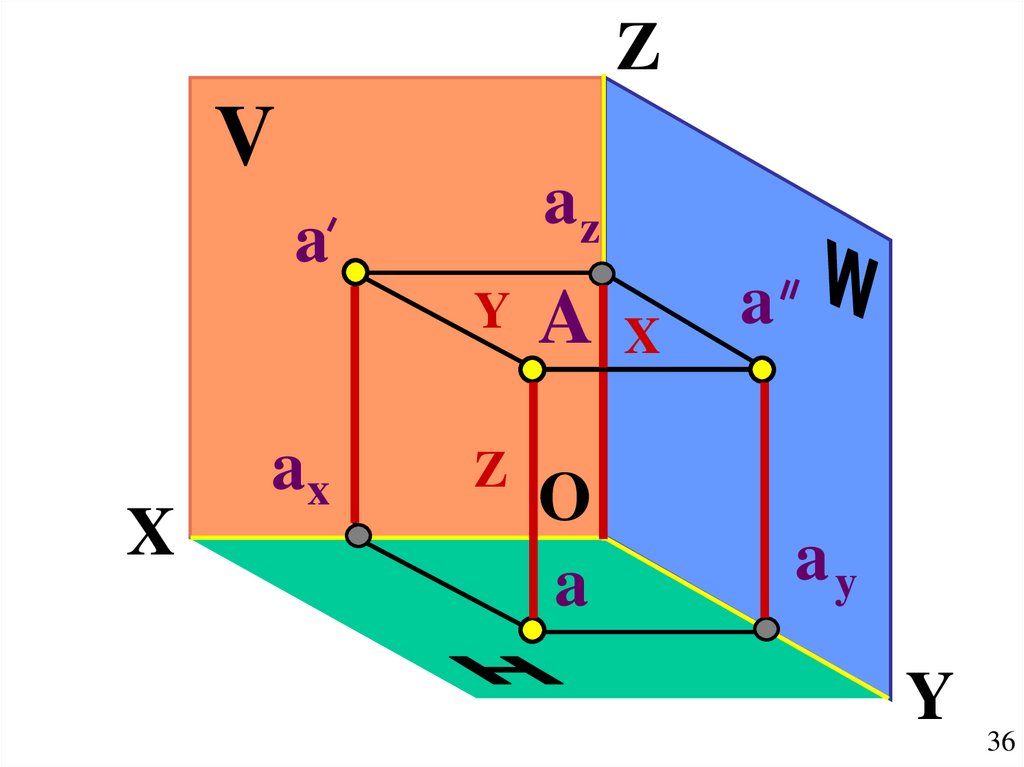
36.
ZV
az
a
X
ax
Y
A
Z
O
a
X
a
ay
Y
36
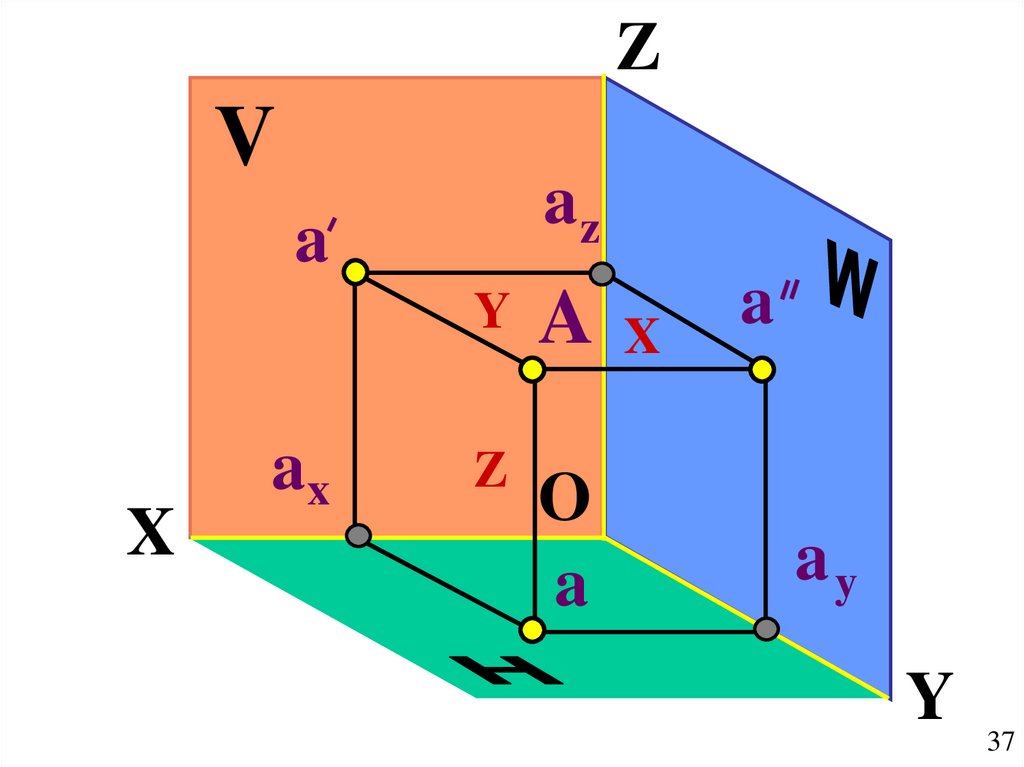
37.
ZV
az
a
X
ax
Y
A
Z
O
a
X
a
ay
Y
37
38.
A (x,y,z)a (x,y)
a (x,z)
a (y,z)
38
39.
ZV
X
O
Y
39
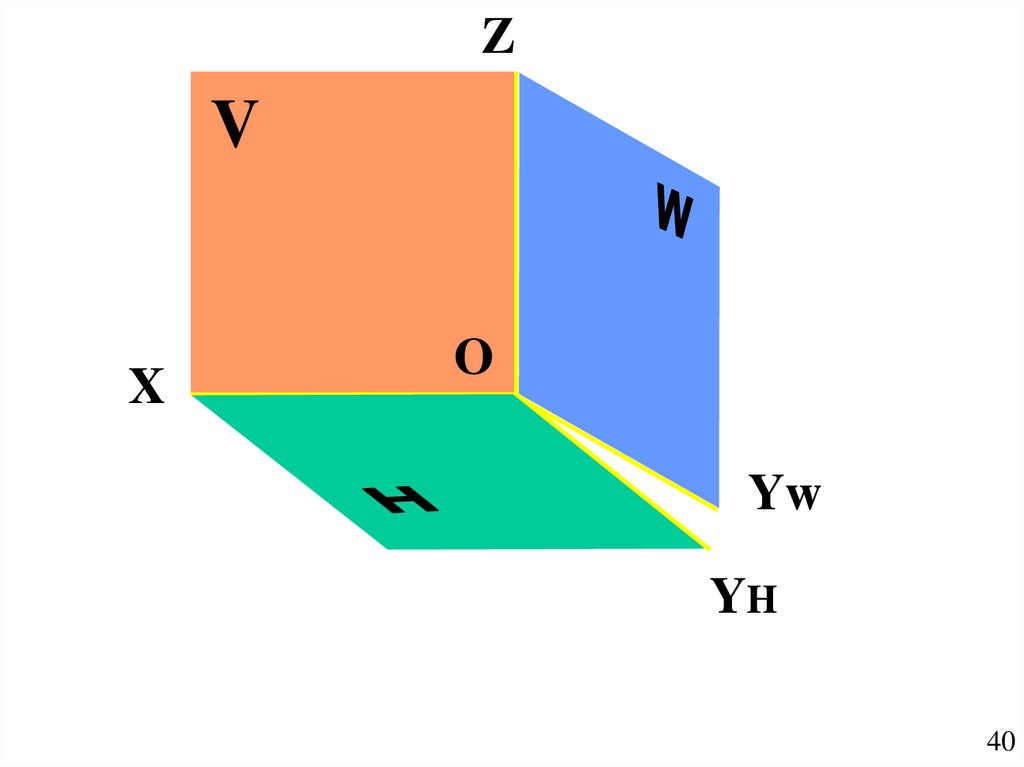
40.
ZV
X
O
Yw
YH
40
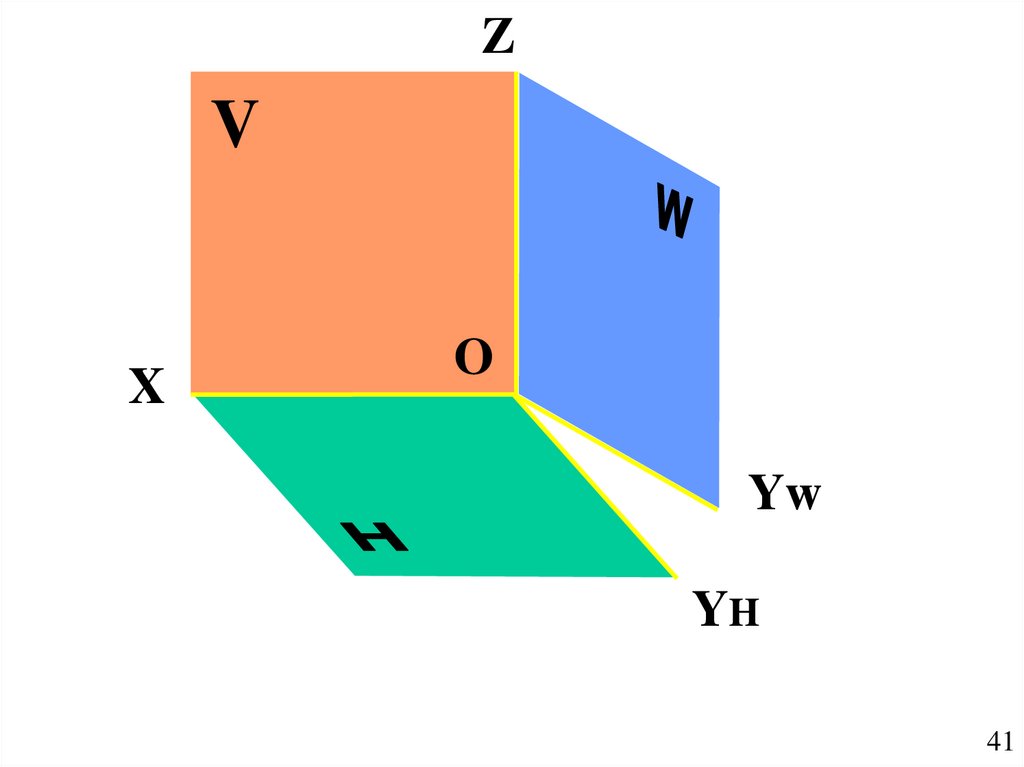
41.
ZV
X
OO
Yw
YH
41
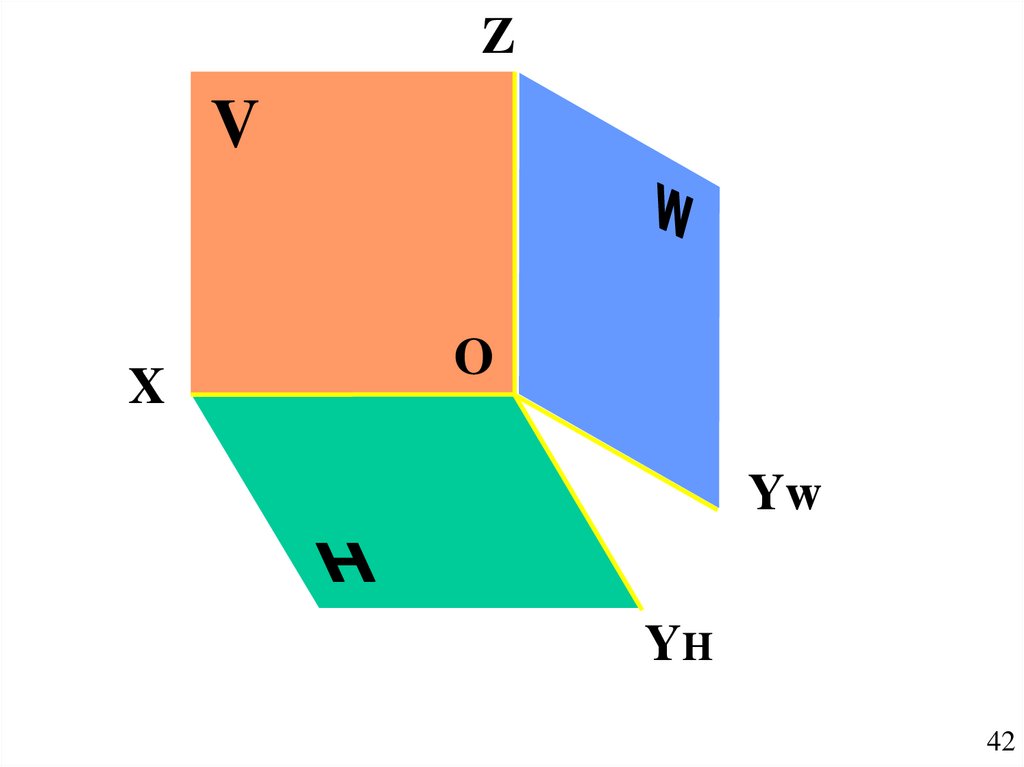
42.
ZV
X
OO
Yw
YH
42
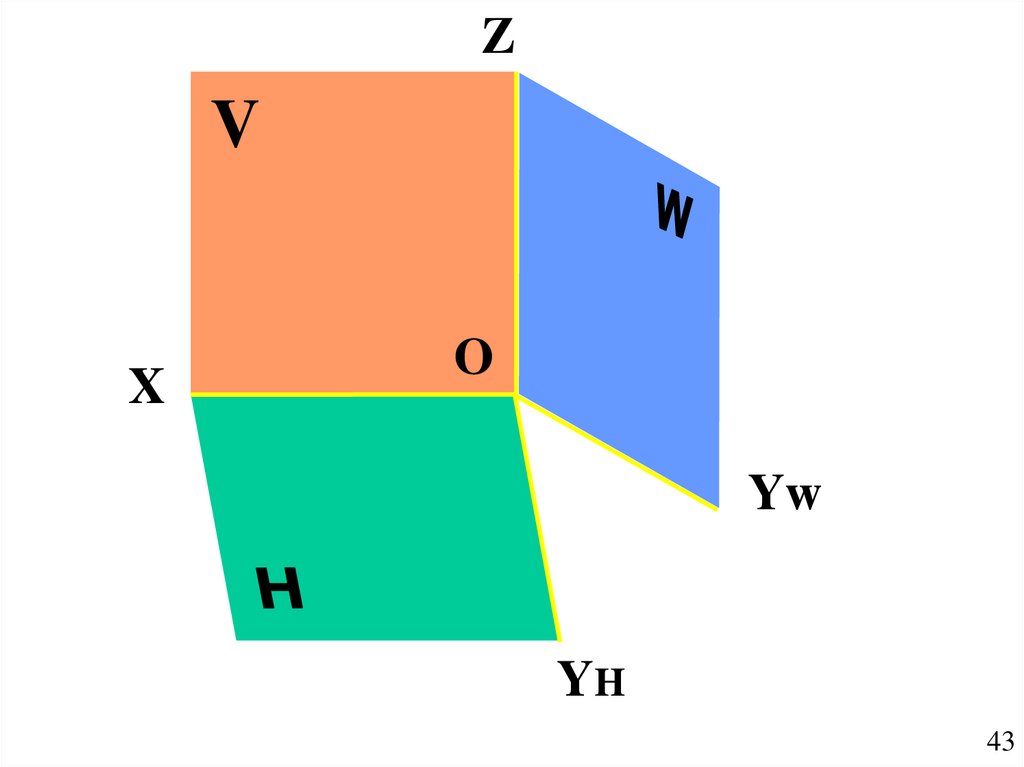
43.
ZV
X
O
Yw
YH
43
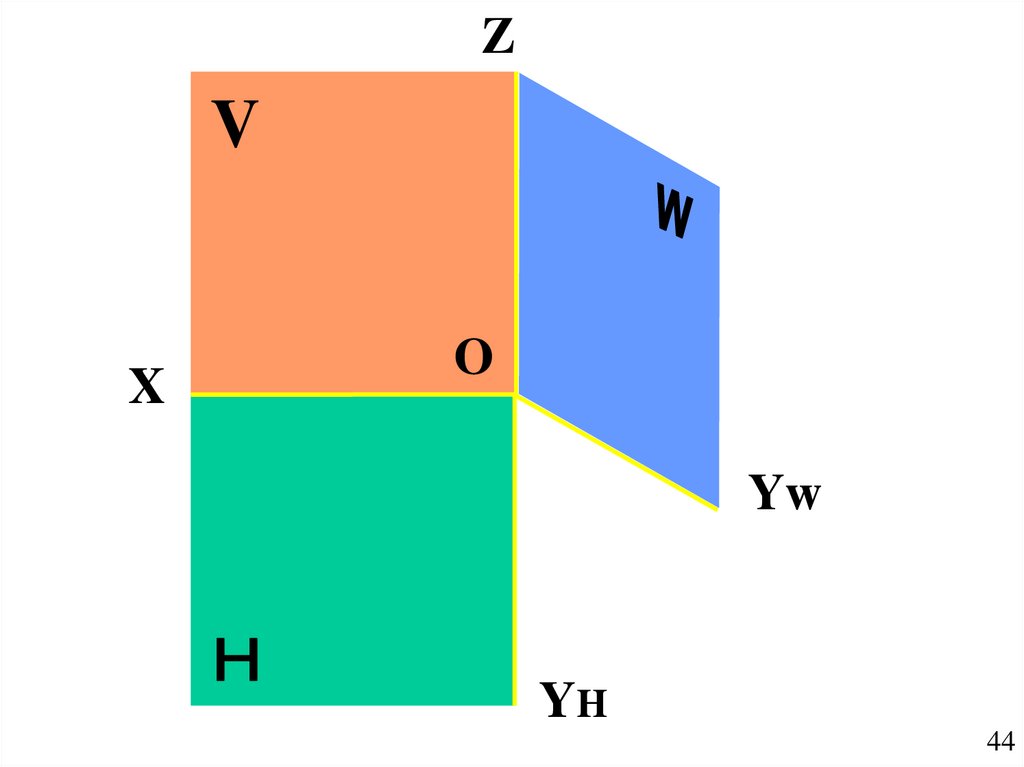
44.
ZV
X
O
Yw
YH
44
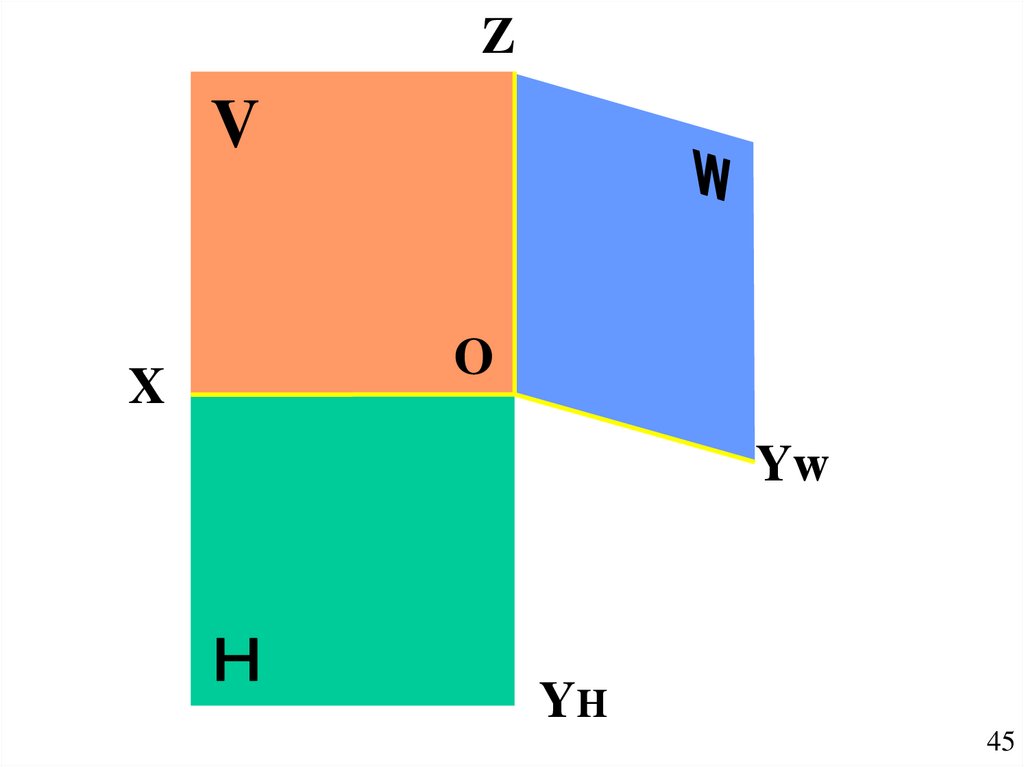
45.
ZV
X
O
Yw
YH
45
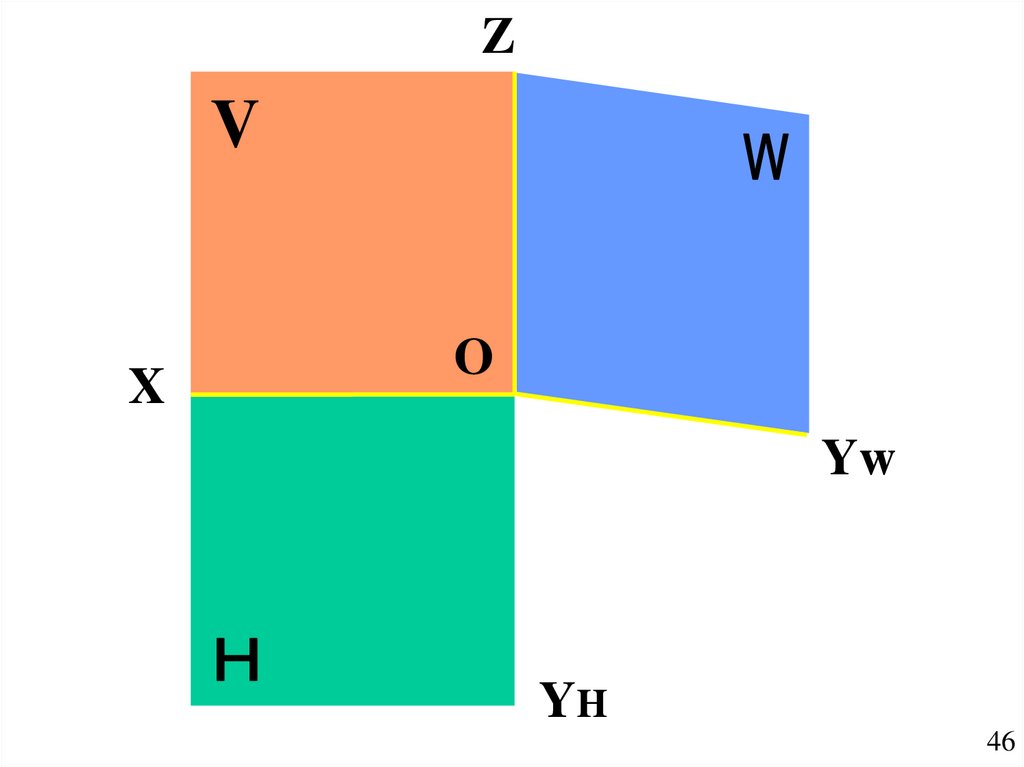
46.
ZV
X
O
Yw
YH
46
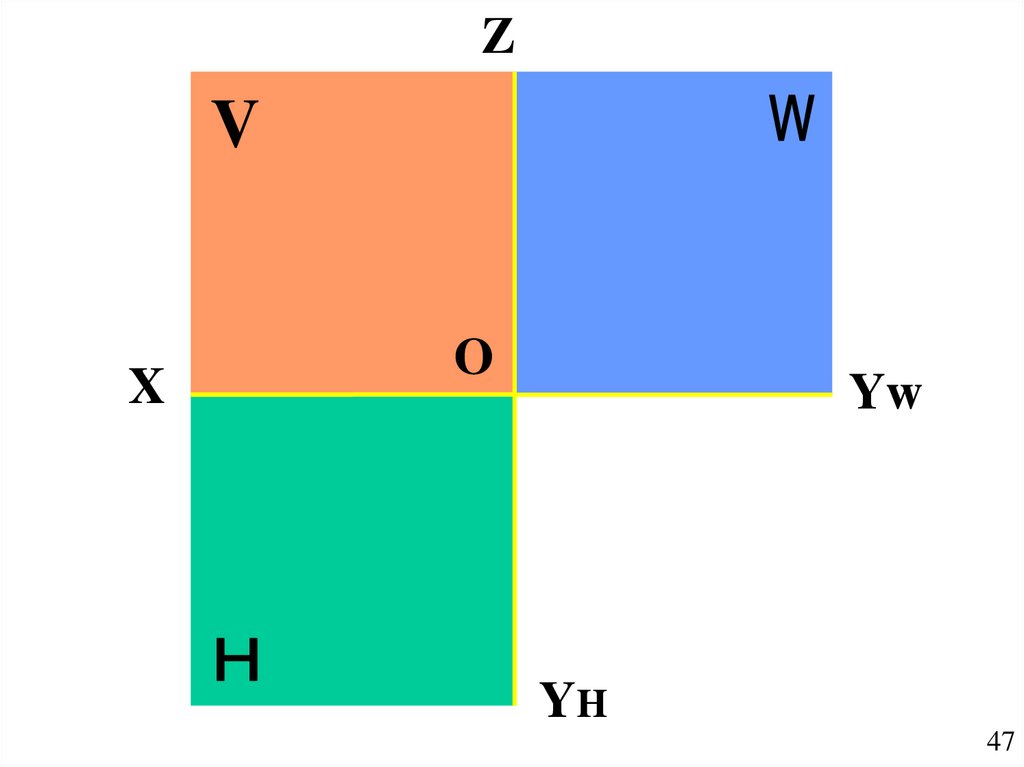
47.
ZV
X
O
Yw
YH
47
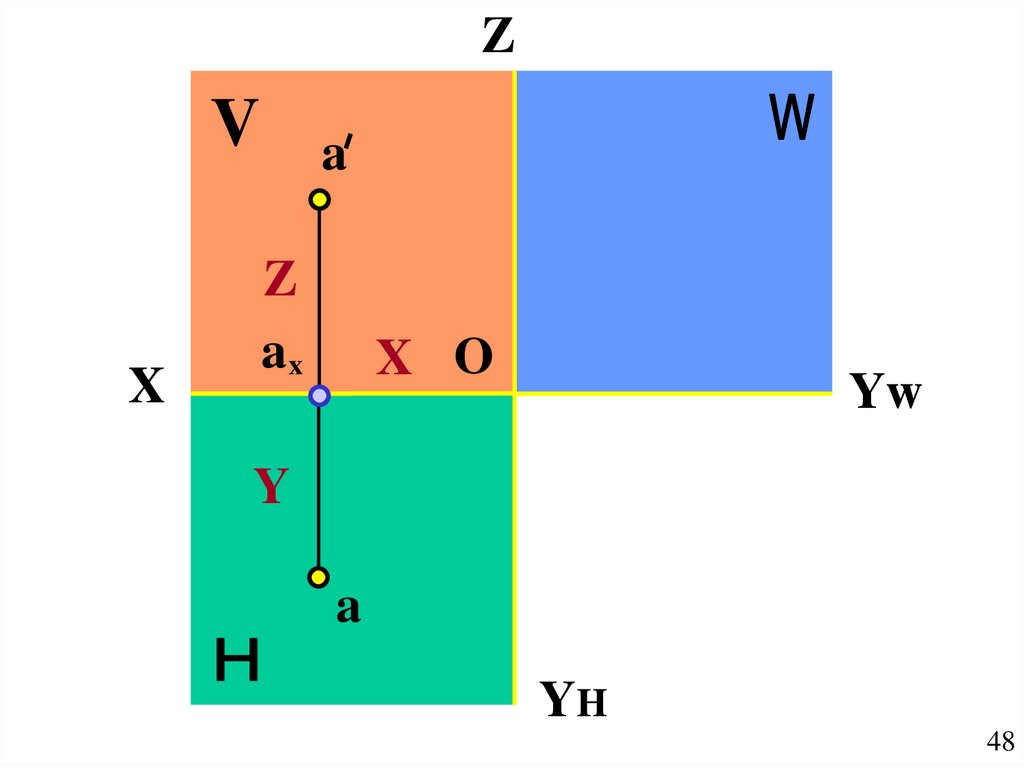
48.
ZV
X
a
Z
ax
X O
Yw
Y
a
YH
48
49.
ZV
X
a
Z
ax
az
a
X O
aY
W
45
Y
a
Yw
aY
H
YH
49
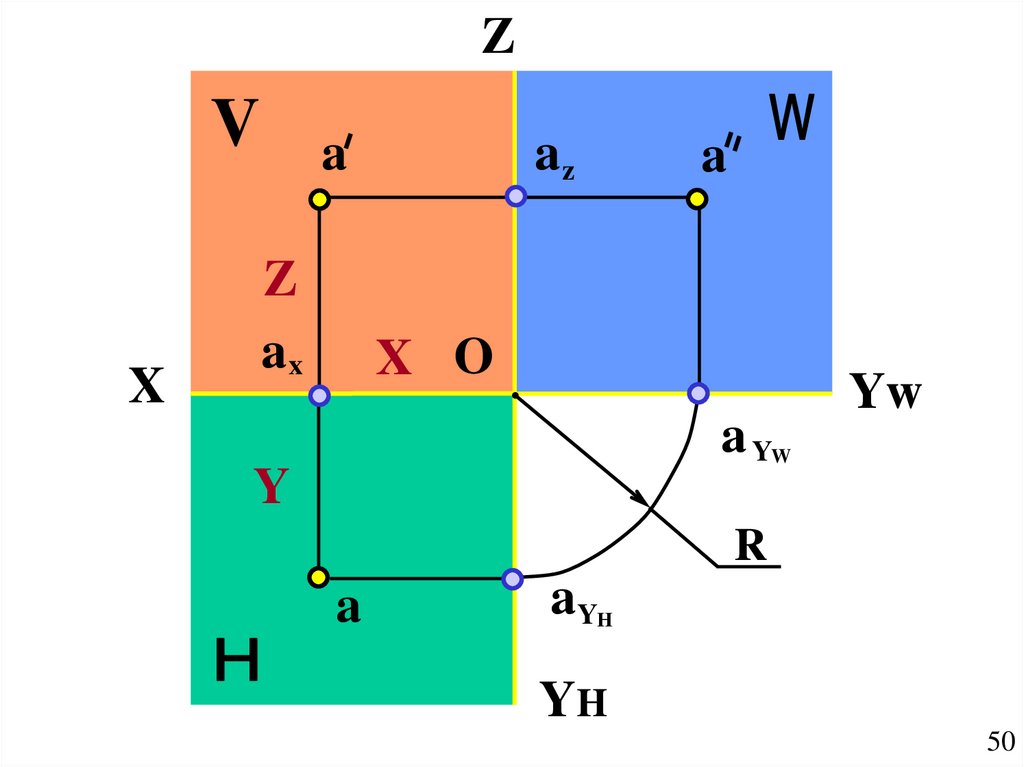
50.
ZV
X
a
Z
ax
az
a
X O
aY
Yw
W
Y
R
a
aY
H
YH
50
51.
1. Положение точкив пространстве
определяется
тремя
координатами
A(x,y,z)
51
52.
2. Положение точкина плоскости
определяется двумя
координатами
a(x,y) , a (x,z) , a (y,z)
52
53.
3. Две проекцииточки определяют
ее положение в
пространстве
53
54.
4. Две проекцииточки лежат на
одном
перпендикуляре
к оси их
разделяющей
54
55. Прямая линия
5556.
Линия – этомножество всех
последовательных
положений двигающейся
точки
Прямая линия – линия,
образованная движением
точки не меняющей
своего направления
56
57.
Прямаялиния задается:
1.Двумя точками ей
принадлежащими
2.Одной точкой и
направлением линии
57
58.
Прямая общегоположения –
прямая, наклоненная
ко всем трем
плоскостям проекций
58
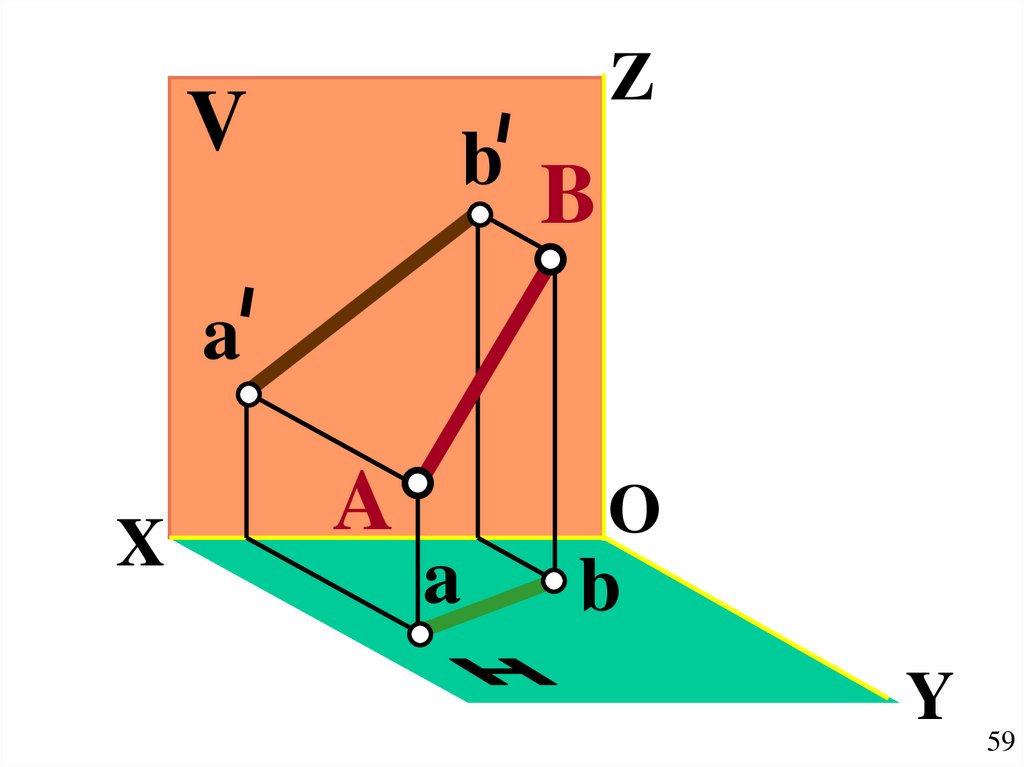
59.
ZV
b
B
a
X
A
O
a
b
Y
59
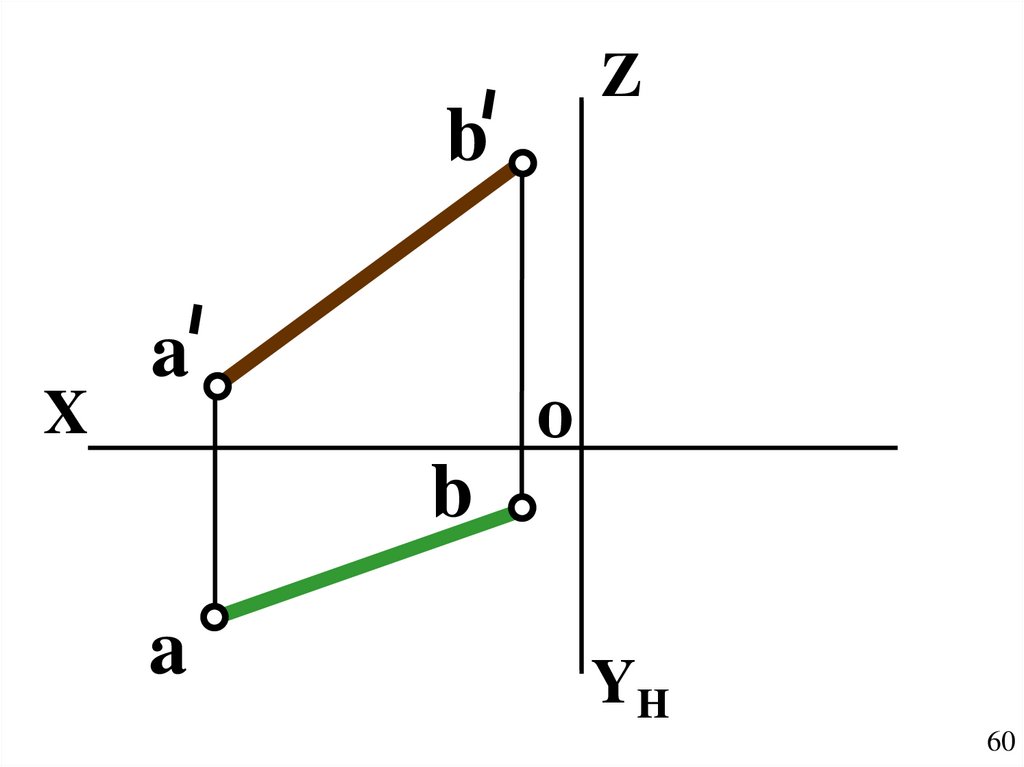
60.
Zb
X
a
о
b
a
YH
60
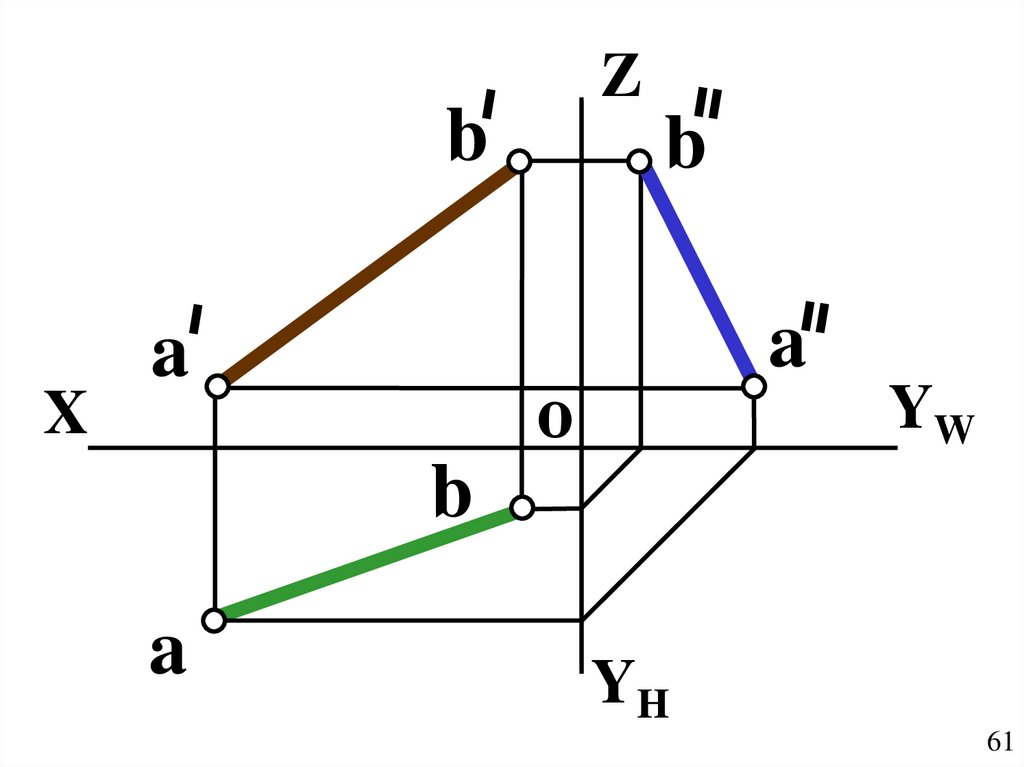
61.
Zb
X
a
b
a
о
YW
b
a
YH
61
62.
Прямые частногоположения –
прямые параллельные
или перпендикулярные
плоскости проекций
62
63.
Прямые частногоположения можно
разделить на:
•Прямые уровня,
•Проецирующие
прямые
63
64. Прямые параллельные плоскости проекции (прямые уровня)
6465.
Горизонтальная прямаяZ
V
b
a
B
A
O
X
a
b
Y
65
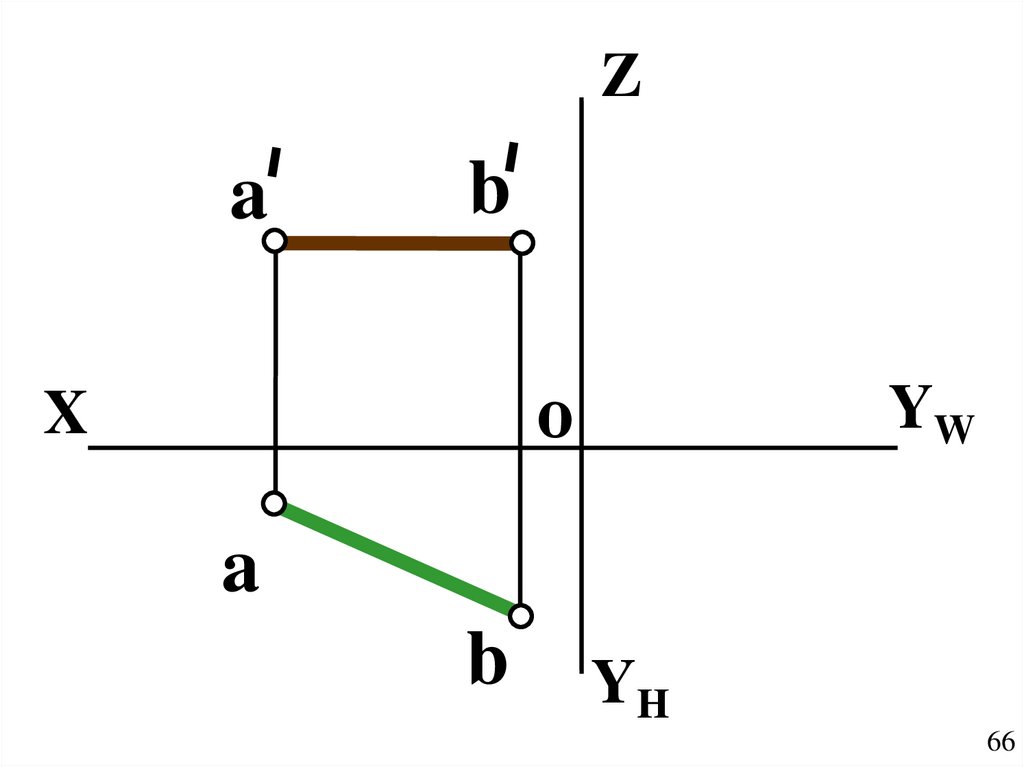
66.
Za
b
о
X
YW
a
b
YH
66
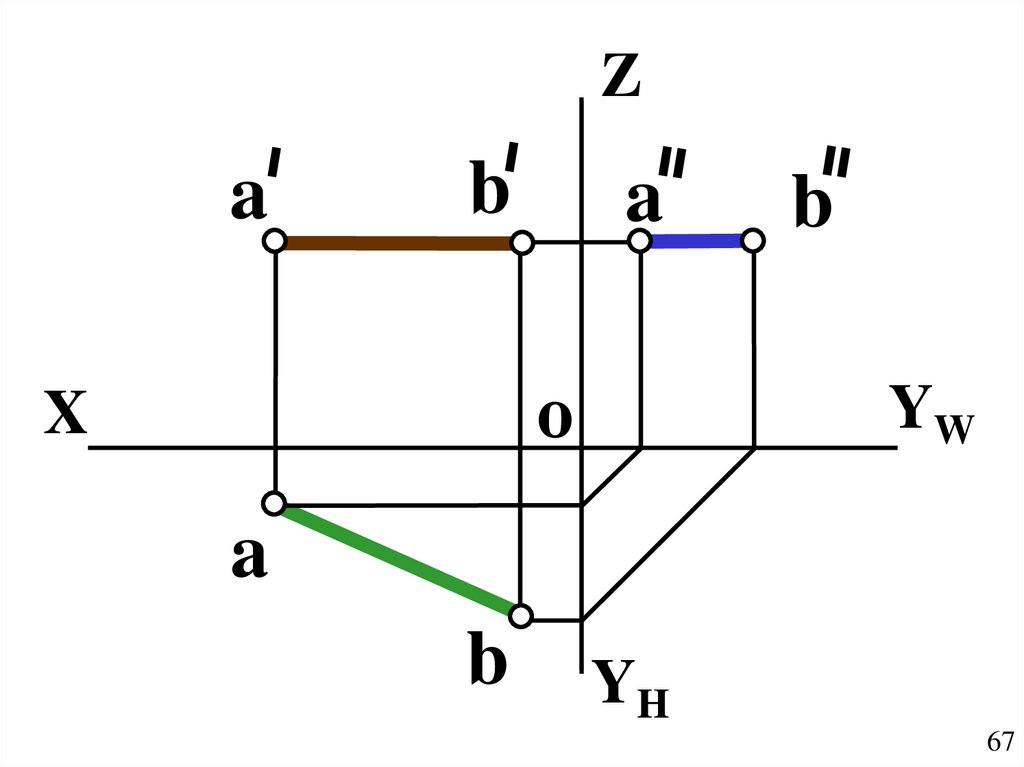
67.
Za
b
a
о
X
b
YW
a
b
YH
67
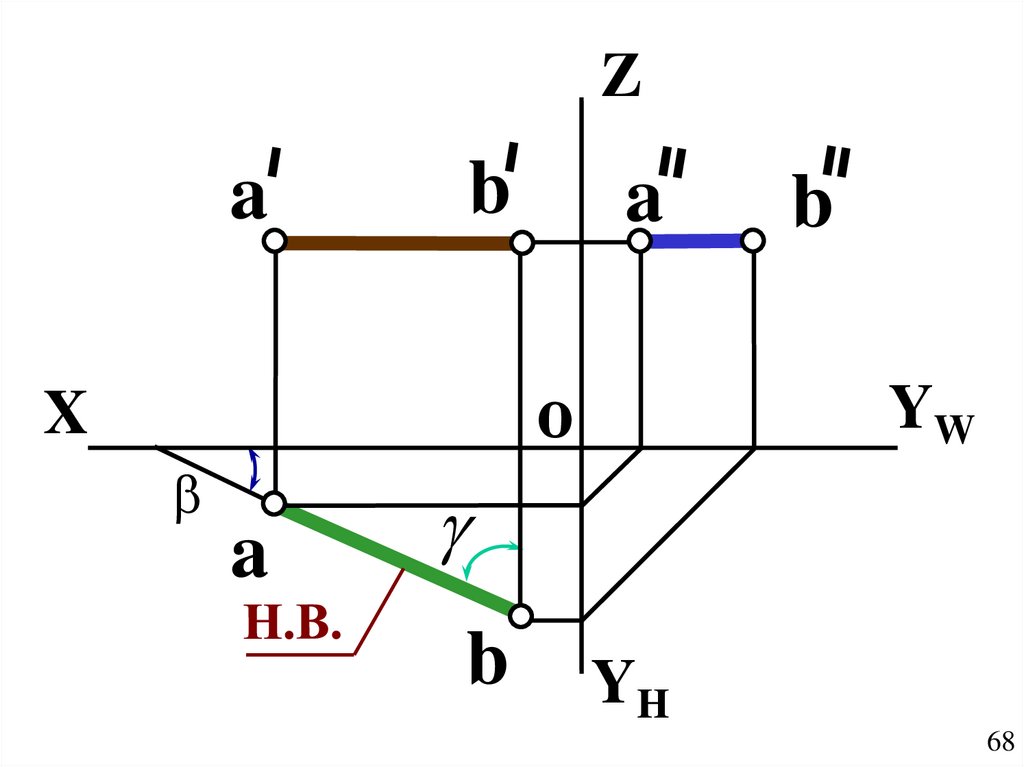
68.
Zb
a
a
о
X
a
b
YW
b
YH
68
69.
Свойства проекцийab AB ;
a b // OX ,( a b ) // OY ;
( AB V ) ( ab OX ) ;
( AB W ) ( ab OYH ) .
69
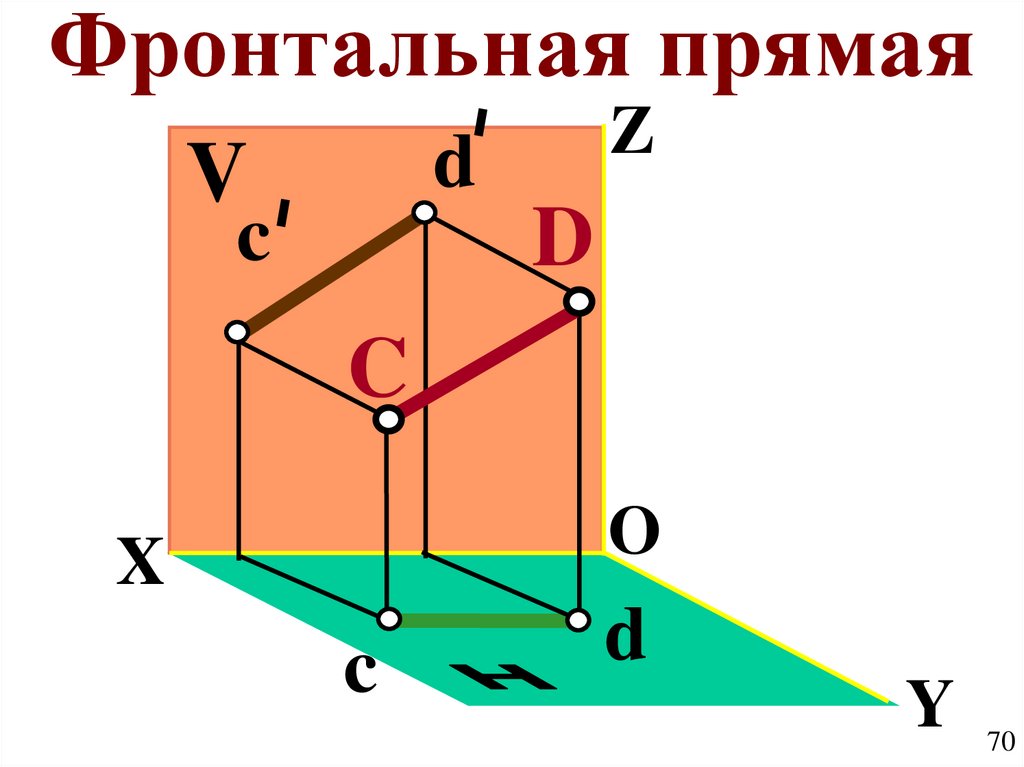
70.
Фронтальная прямаяZ
d
V
D
c
C
O
X
c
d
Y
70
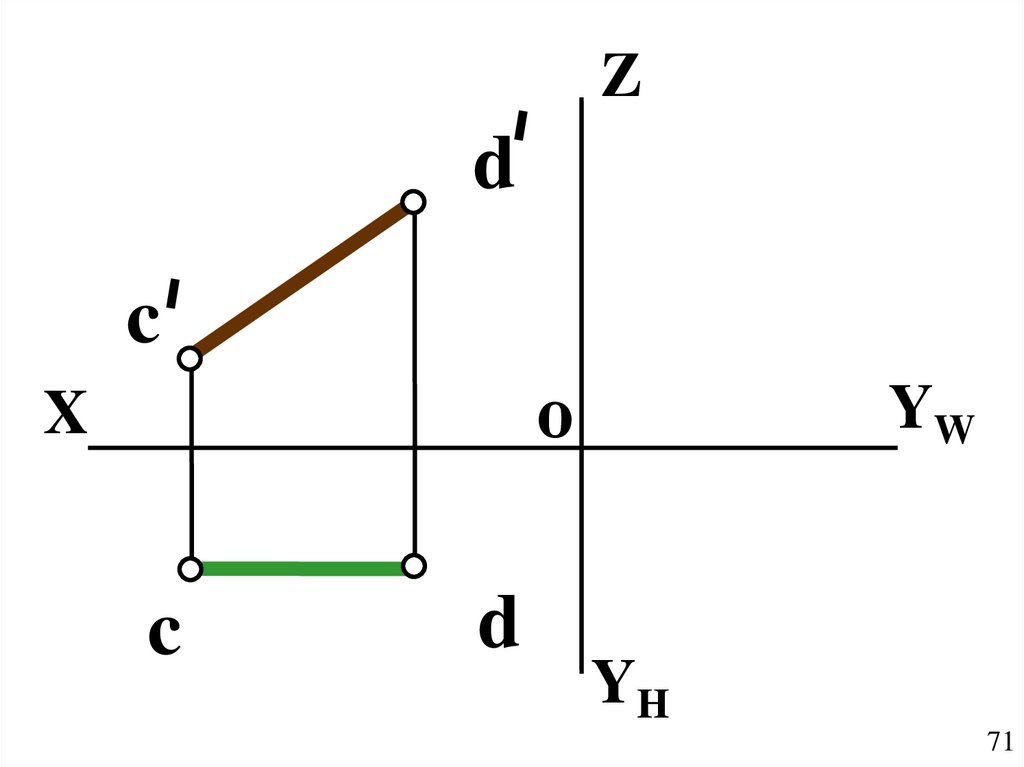
71.
Zd
c
о
X
c
d
YW
YH
71
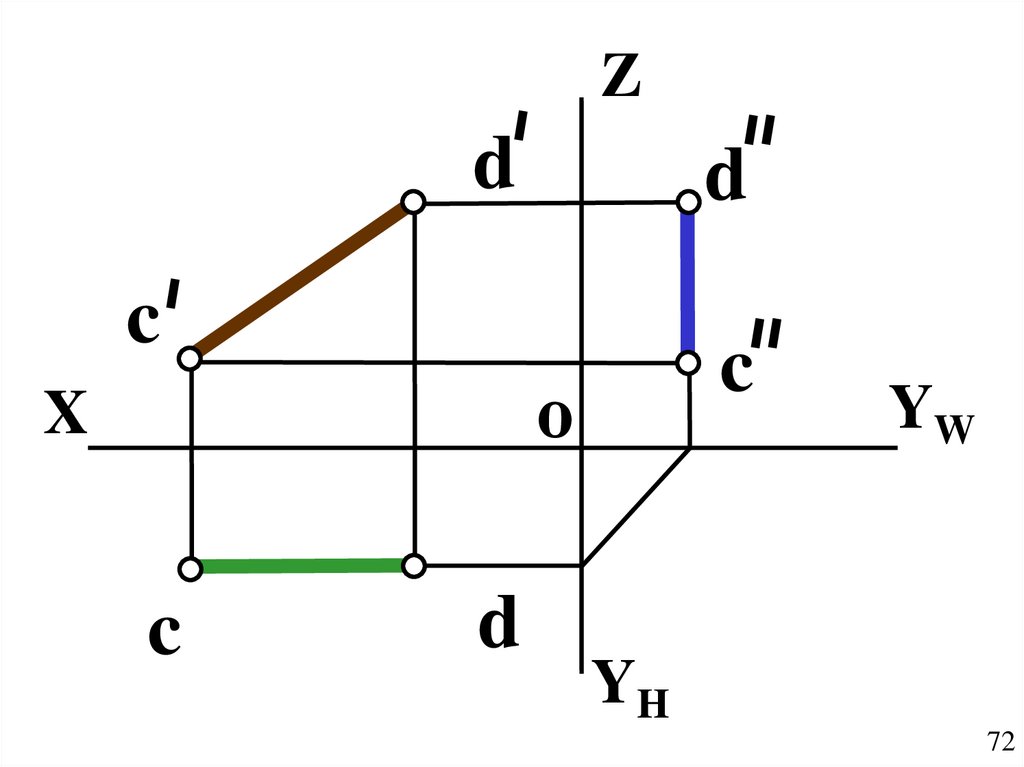
72.
Zd
d
c
c
о
X
c
d
YW
YH
72
73.
Zd
d
c
c
о
X
c
d
YW
YH
73
74.
Свойства проекцийc d CD ;
cd // OX , c d // OZ ;
( CD H ) ( c d OX ) ;
( CD W ) ( c d OZ ) .
74
75.
Если прямая параллельнаплоскости проекций,
то на эту плоскость в
натуральную величину
проецируется сама
прямая и углы наклона
её к двум другим
плоскостям проекций
75
76.
Проекции прямойна две другие
плоскости проекций,
параллельны осям,
определяющим данную
плоскость
76
77. Прямые перпендикулярные плоскостям проекций (проецирующие прямые, двояко параллельные прямые)
7778.
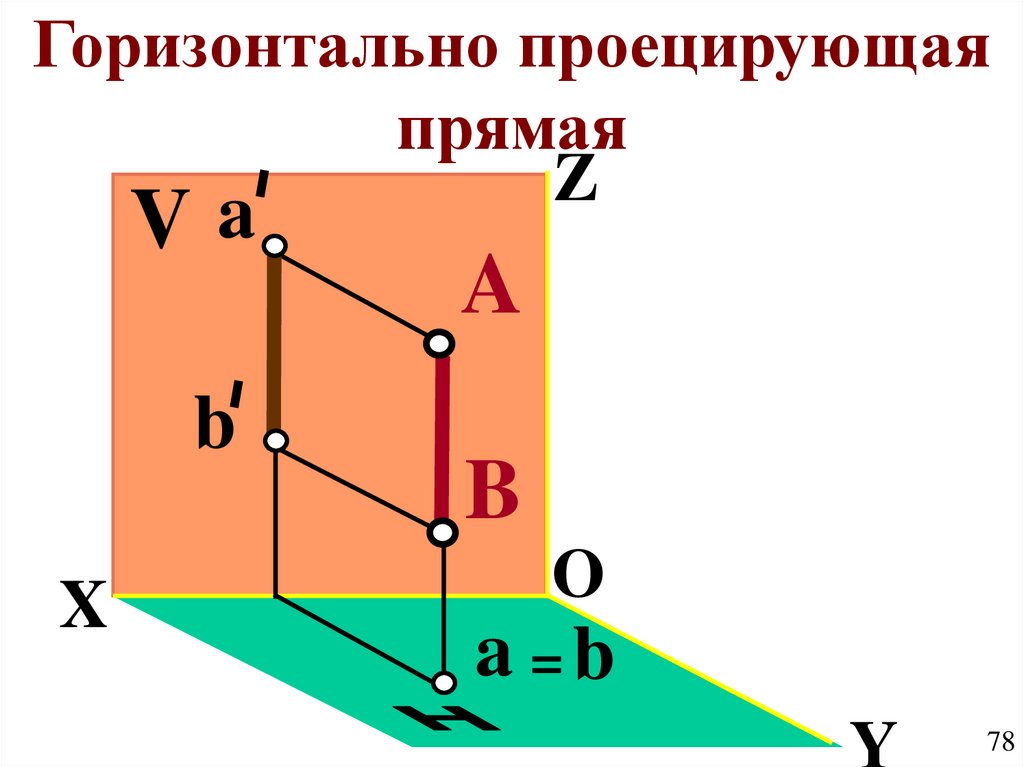
Горизонтально проецирующаяпрямая
Z
Va
b
X
A
B
O
a =b
Y
78
79.
Свойства проекций( AB ) H , ( AB ) // V , ( AB ) // W ;
ab -точка;
a b a b AB ;
( a b ) OX , ( a b ) OYW
79
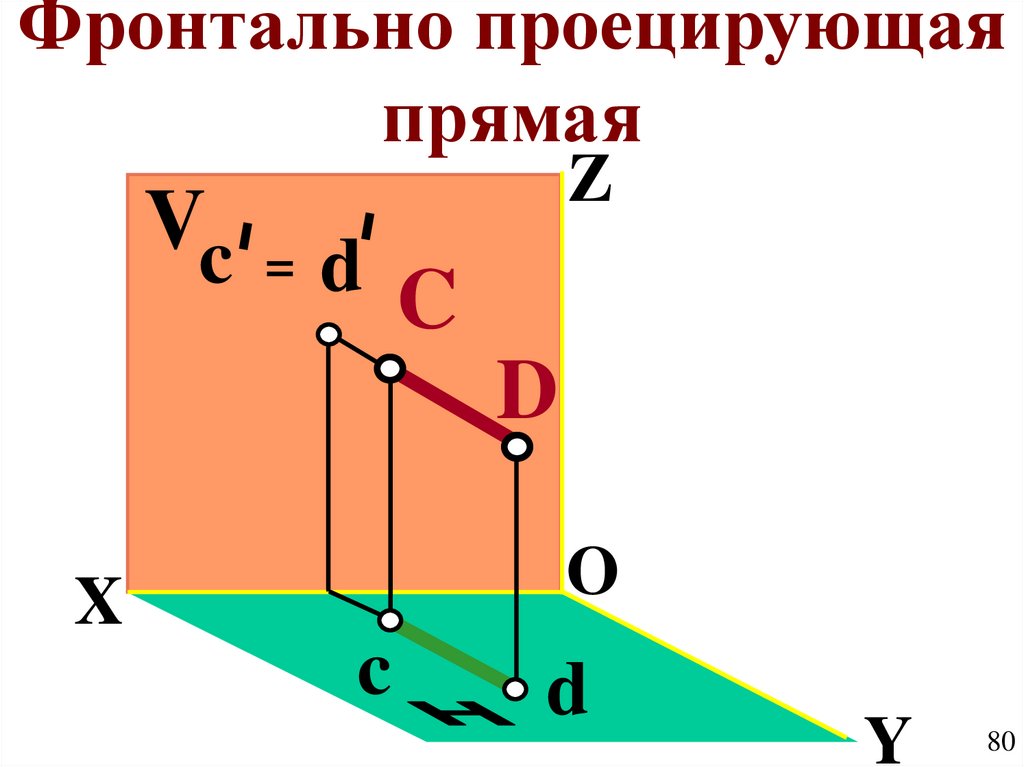
80.
Фронтально проецирующаяпрямая
Vc
Z
=
d C
D
O
X
c
d
Y
80
81.
Свойства проекций( CD ) V , ( CD ) // H , ( CD ) // W ;
c d - точка;
cd c d CD ;
( cd ) OX , ( c d ) OZ
81
82.
Если прямаяперпендикулярна
плоскости проекции,
то на эту плоскость она
проецируется в точку
82
83. Проекции прямой на две другие плоскости проекций, перпендикулярны осям, определяющим данную плоскость. Эти проекции равны
натуральной величинеотрезка
83














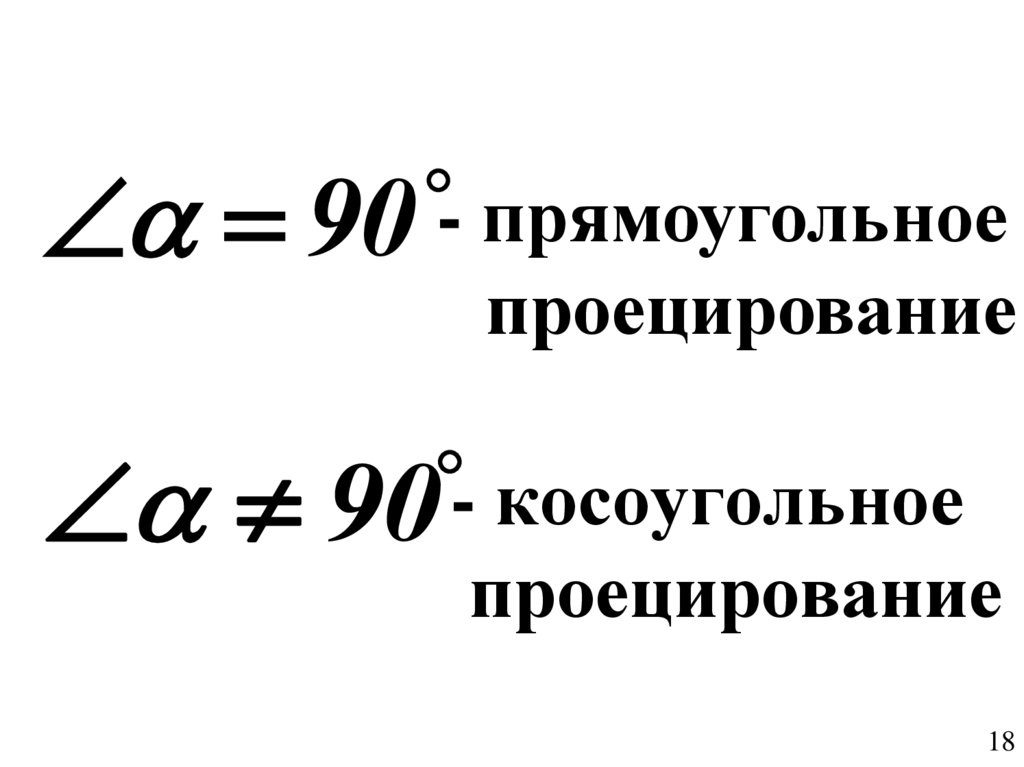





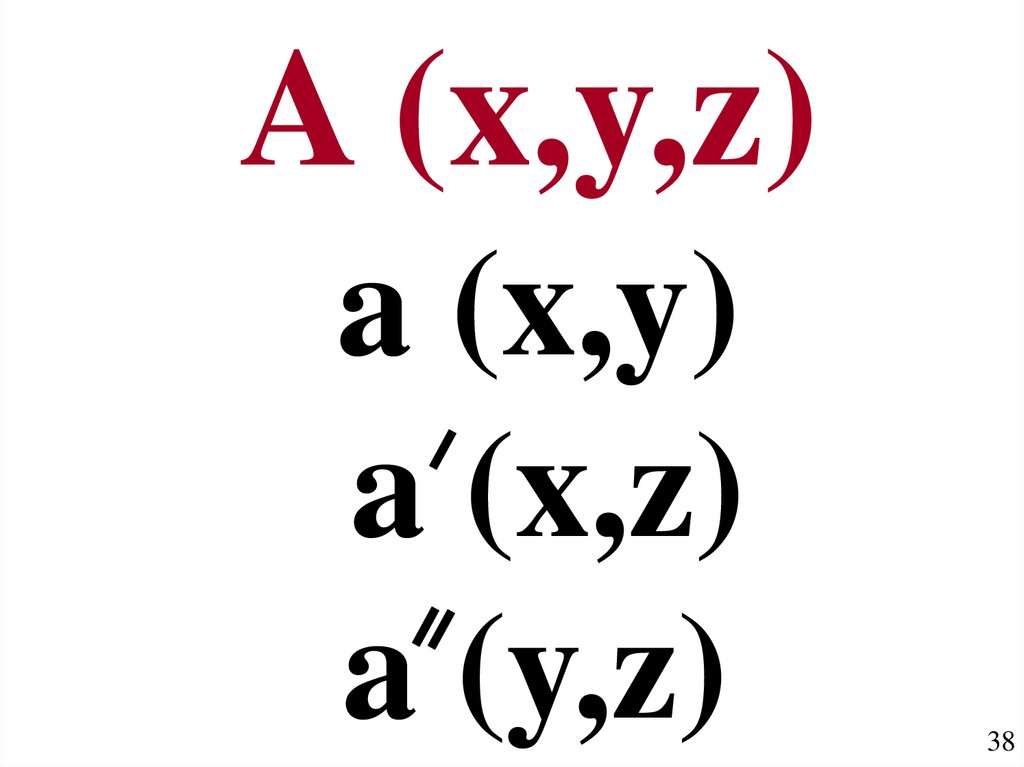













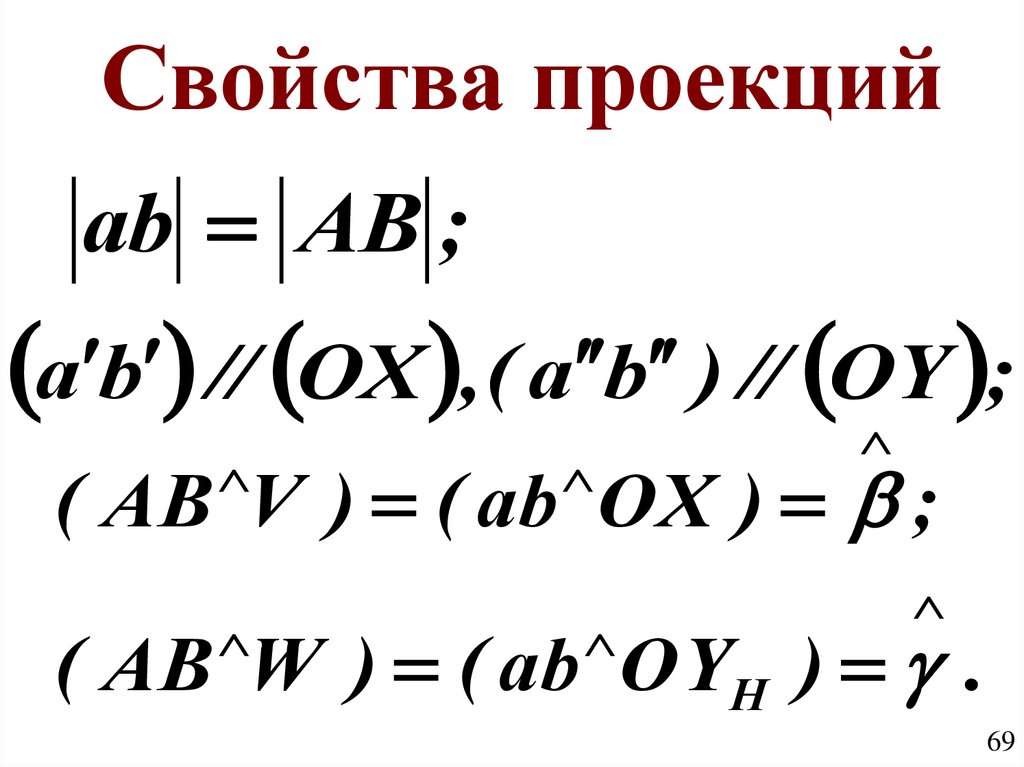









 Инженерная графика
Инженерная графика








