Похожие презентации:
Начертательная геометрия. Виды проецирования
1. Начертательная геометрия
• В 1795 годуфранцузский геометр
Гаспар Монж впервые
систематизировал и
изложил методы
начертательной
геометрии – науки,
изучающей
геометрические
способы изображения
предметов на
плоскости. С этого
времени чертеж стал
международным языком
инженеров.
2. Если посадить человека между горящей лампой и экраном из тонкой бумаги, обвести карандашом контур тени, то мы получим силуэтный
портрет. Такое теневое изображение можноиспользовать не только для выполнения портретов и картин, но
для изображения различных пространственных тел. Однако такой
способ не дает точных размеров изображения оригинала.
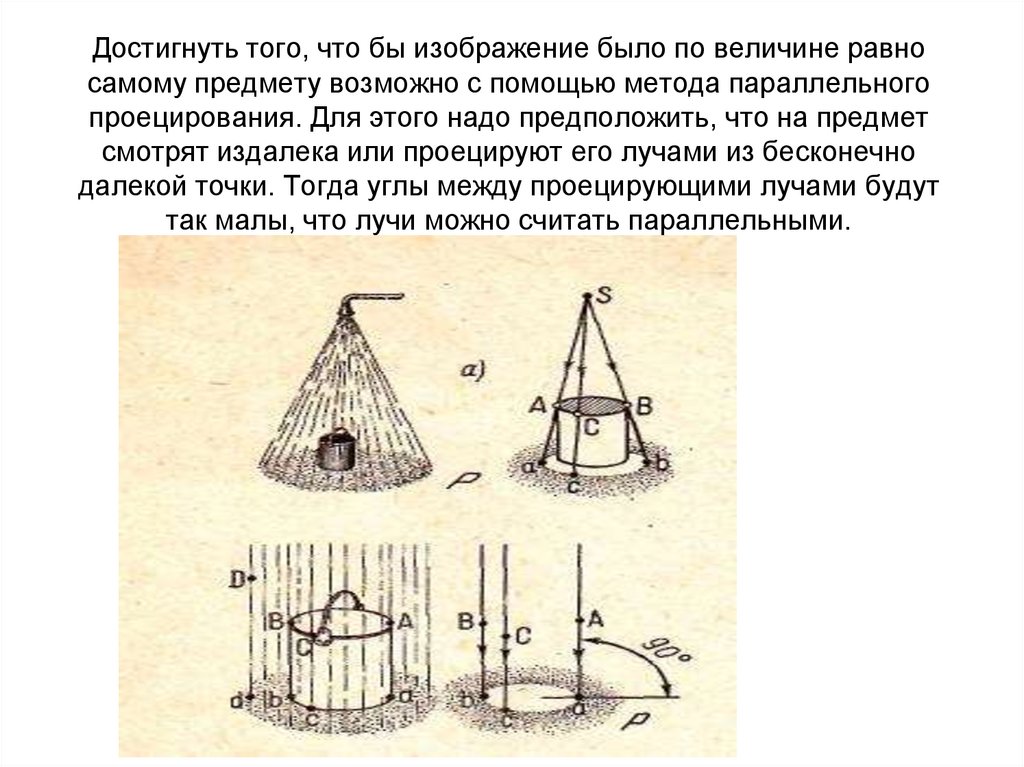
3. Достигнуть того, что бы изображение было по величине равно самому предмету возможно с помощью метода параллельного
проецирования. Для этого надо предположить, что на предметсмотрят издалека или проецируют его лучами из бесконечно
далекой точки. Тогда углы между проецирующими лучами будут
так малы, что лучи можно считать параллельными.
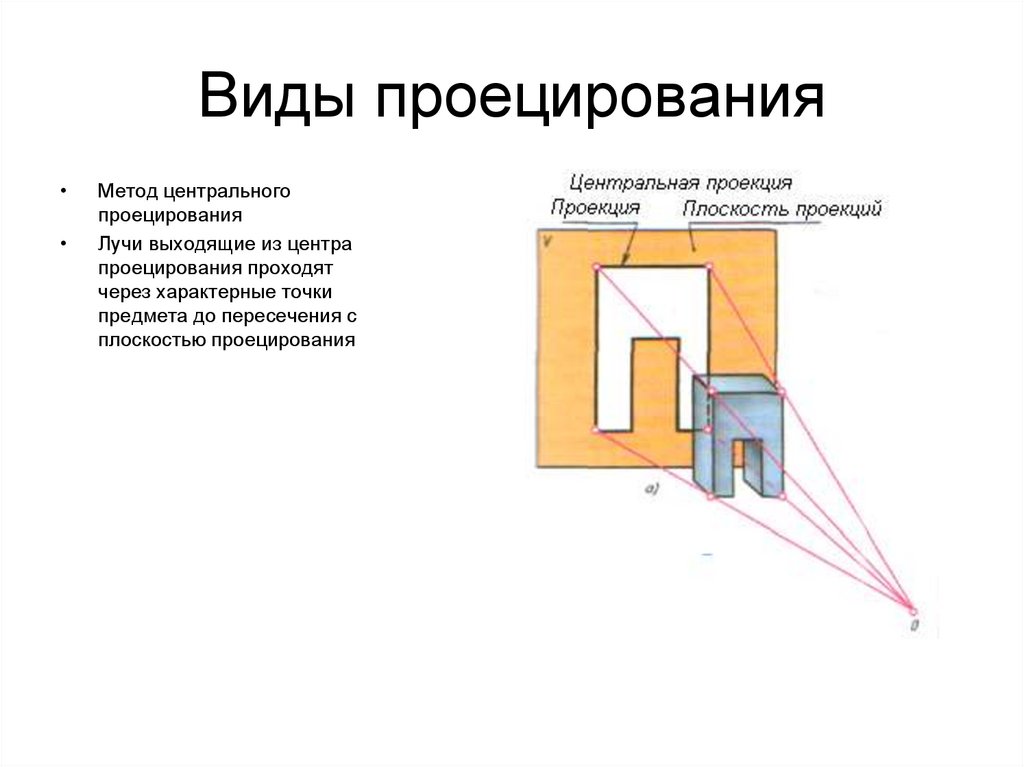
4. Виды проецирования
Метод центрального
проецирования
Лучи выходящие из центра
проецирования проходят
через характерные точки
предмета до пересечения с
плоскостью проецирования
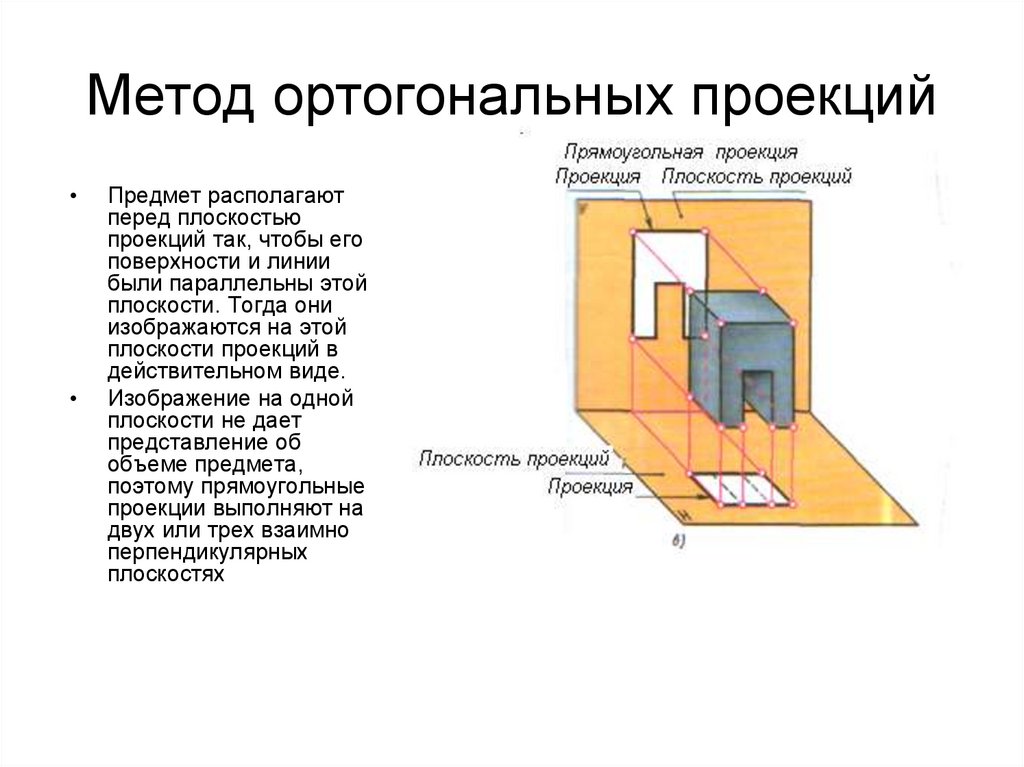
5. Метод ортогональных проекций
Предмет располагают
перед плоскостью
проекций так, чтобы его
поверхности и линии
были параллельны этой
плоскости. Тогда они
изображаются на этой
плоскости проекций в
действительном виде.
Изображение на одной
плоскости не дает
представление об
объеме предмета,
поэтому прямоугольные
проекции выполняют на
двух или трех взаимно
перпендикулярных
плоскостях
6.
7.
Метод ортогональных проекцийПрямоугольные проекции дают
возможность легко определять
размеры предметов и их
положение относительно
плоскостей проекций, по ним не
трудно построить развертки
предметов и решать ряд других
задач. В этом несомненное
достоинство метода
прямоугольных проекций.
Но прямоугольные проекции
недостаточно наглядны. Не имея
навыка трудно представить, что
изображено на рисунке
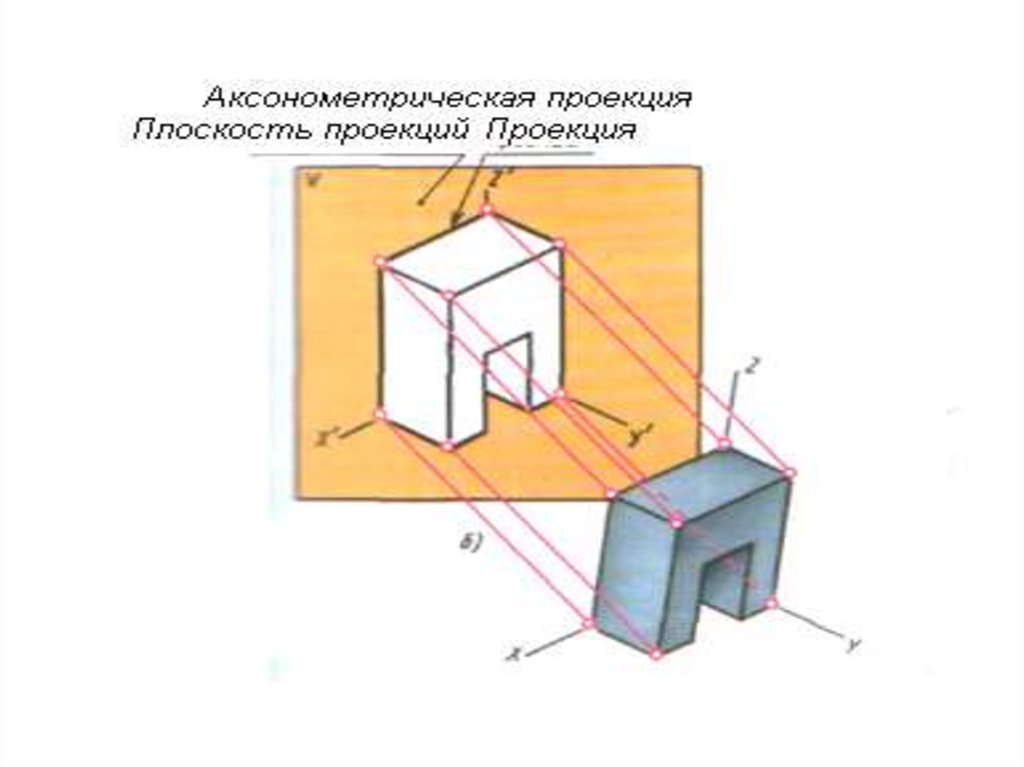
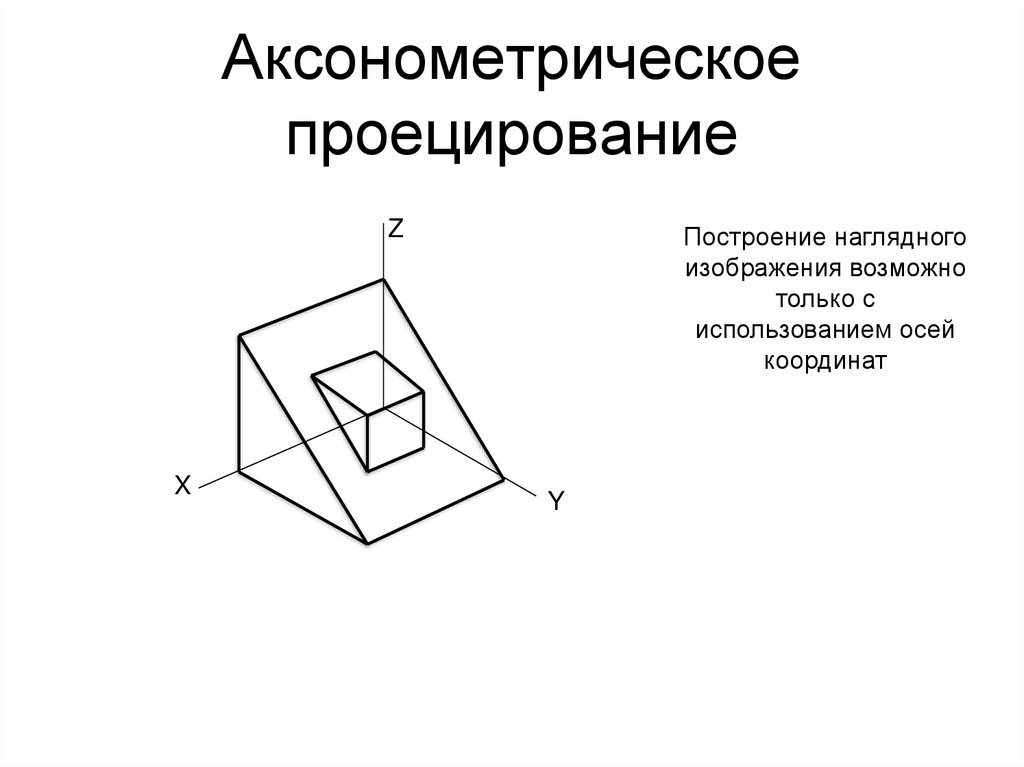
8. Аксонометрическое проецирование
ZX
Построение наглядного
изображения возможно
только с
использованием осей
координат
Y
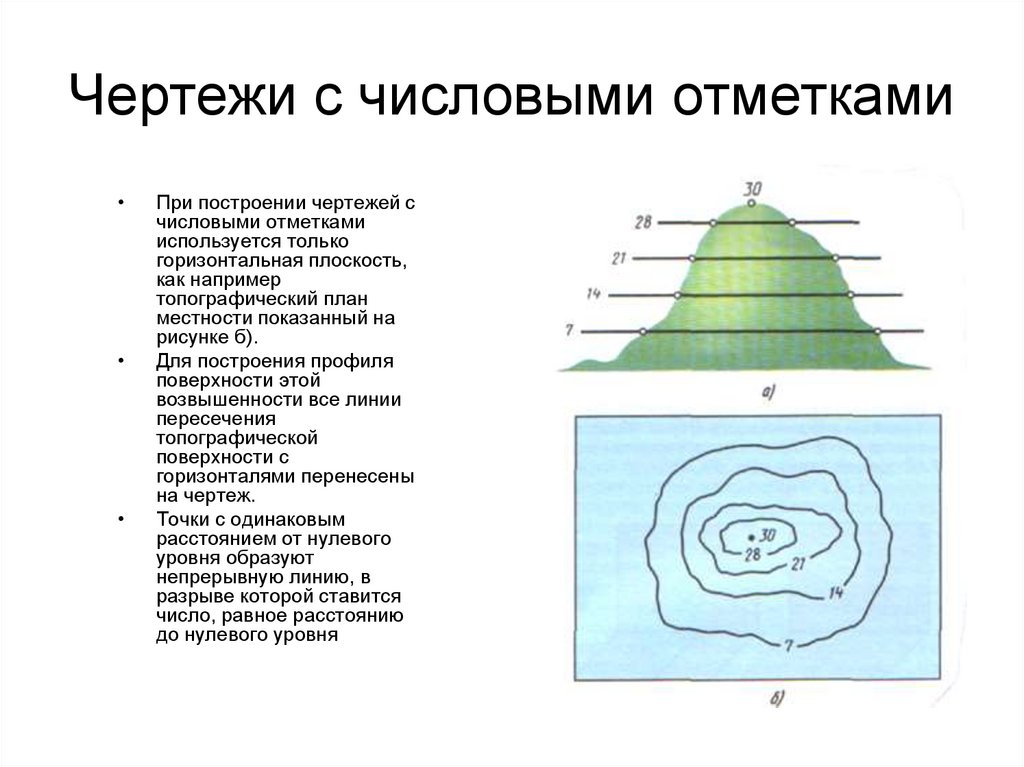
9. Чертежи с числовыми отметками
При построении чертежей с
числовыми отметками
используется только
горизонтальная плоскость,
как например
топографический план
местности показанный на
рисунке б).
Для построения профиля
поверхности этой
возвышенности все линии
пересечения
топографической
поверхности с
горизонталями перенесены
на чертеж.
Точки с одинаковым
расстоянием от нулевого
уровня образуют
непрерывную линию, в
разрыве которой ставится
число, равное расстоянию
до нулевого уровня
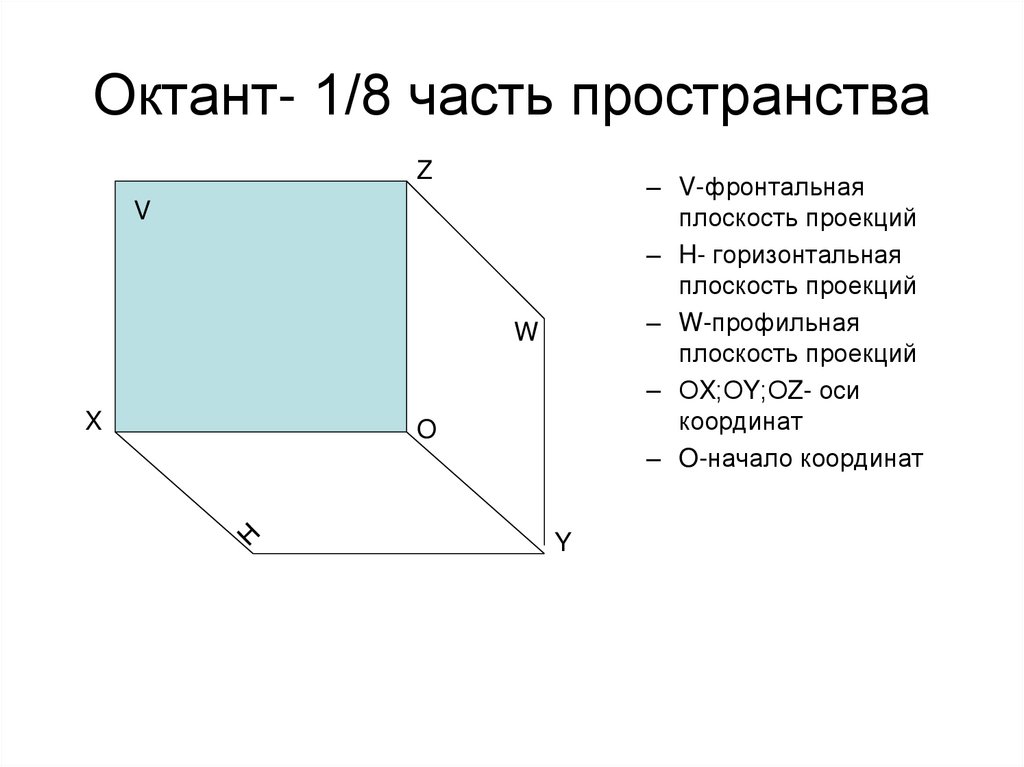
10. Октант- 1/8 часть пространства
Z– V-фронтальная
плоскость проекций
– H- горизонтальная
плоскость проекций
– W-профильная
плоскость проекций
– ОX;ОY;ОZ- оси
координат
– O-начало координат
V
W
X
O
Y
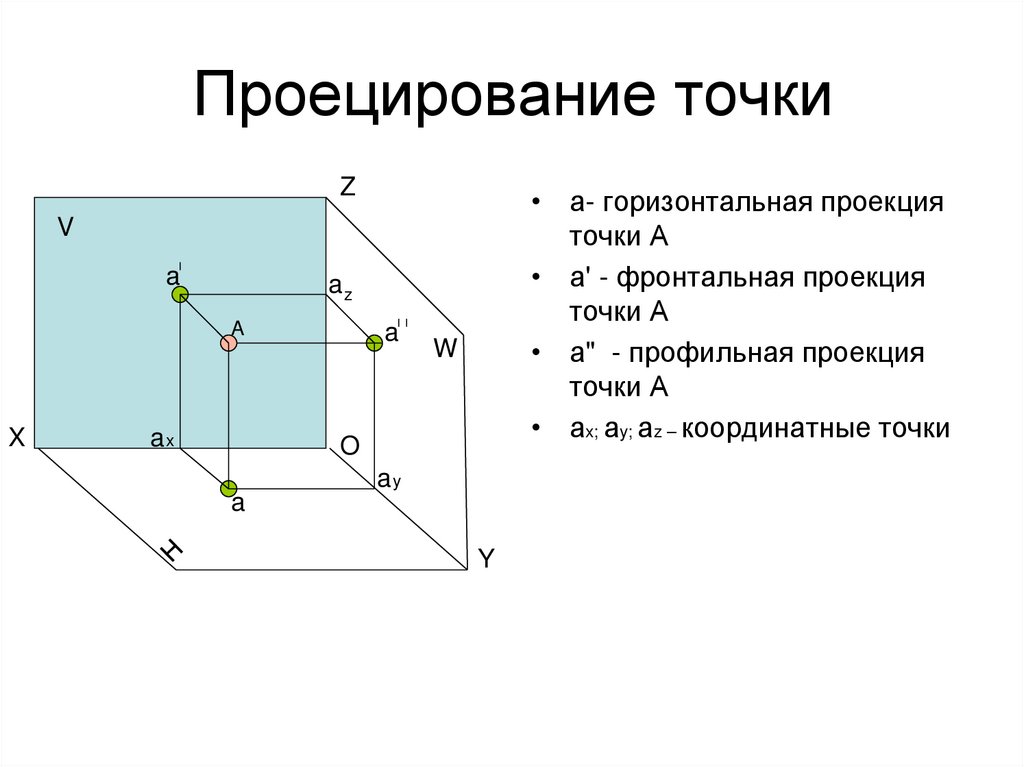
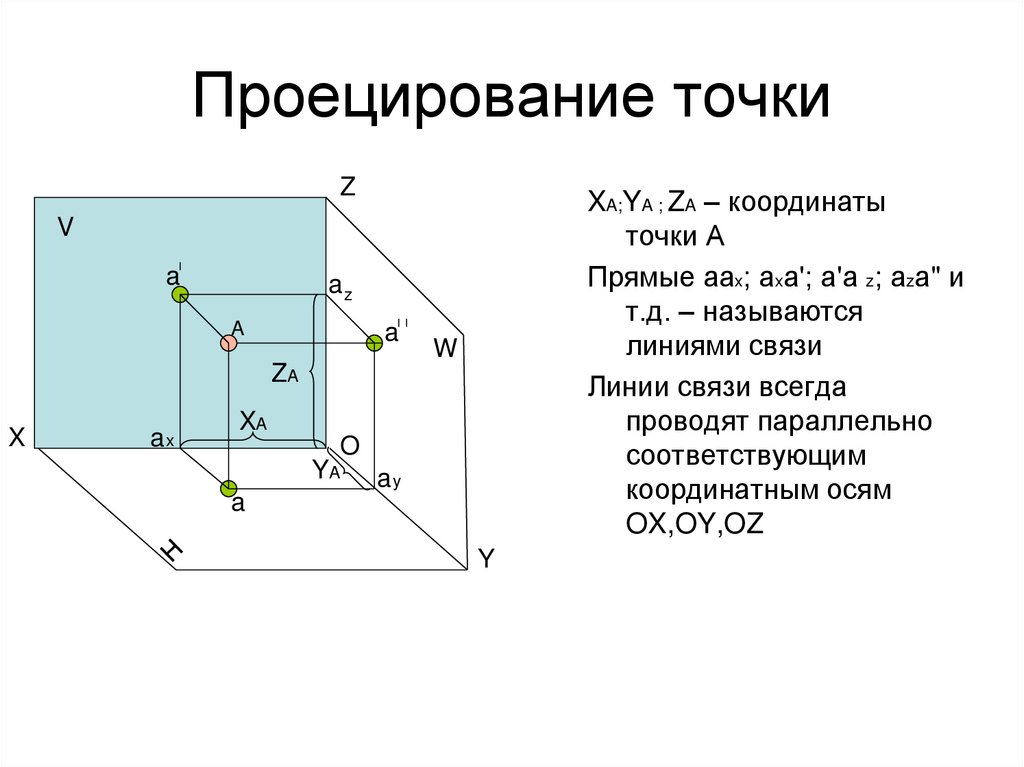
11. Проецирование точки
Z• а- горизонтальная проекция
точки А
• а' - фронтальная проекция
точки А
• а" - профильная проекция
точки А
• аx; аy; аz – координатные точки
V
a
az
A
X
ax
a
W
O
ay
a
Y
12. Проецирование точки
ZXA;YA ; ZA – координаты
точки А
Прямые аах; аха'; а'а z; аzа" и
т.д. – называются
линиями связи
Линии связи всегда
проводят параллельно
соответствующим
координатным осям
OX,OY,OZ
V
a
az
A
a
W
ZA
X
ax
XA
O
YA
ay
a
Y
13. Построение эпюра точки (комплексный чертеж)
ZZ
V
V
a
a
az
A
W
a
az
W
ZA
X
ax
a
ZA
XA
X
O
YA
XA
aX
ay
YA
YA
O
a
a
ay
Y
H
Y
ay
Y
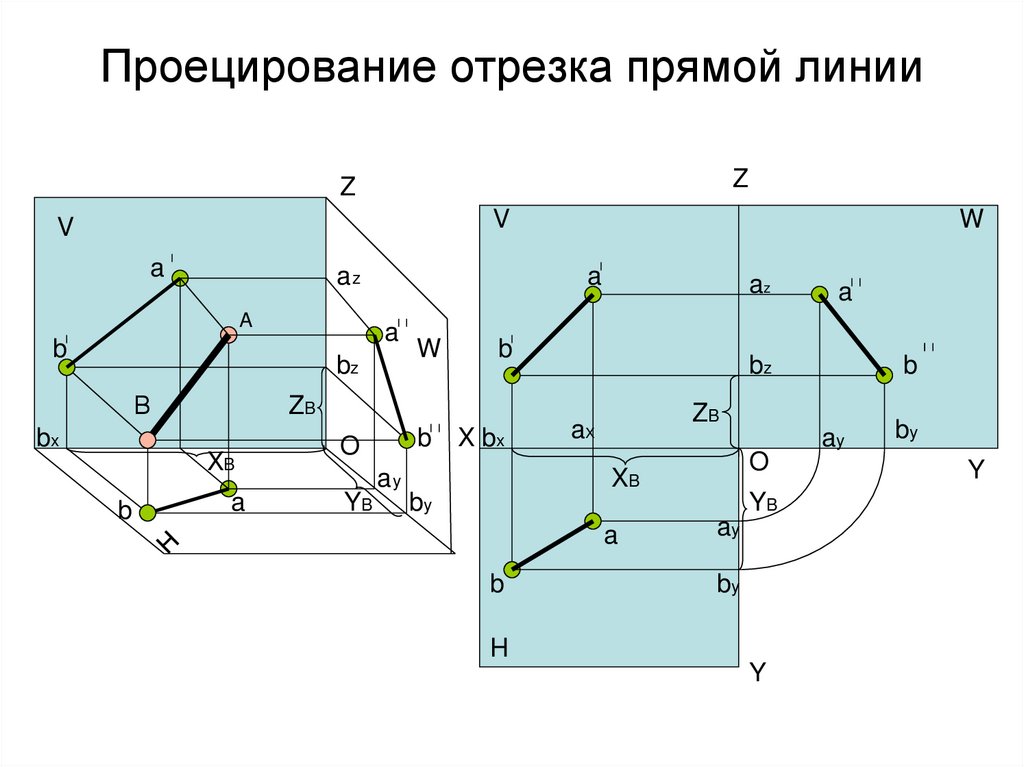
14. Проецирование отрезка прямой линии
ZZ
V
V
a
az
A
a
a
b
bz
В
W
az
b
XB
a
b
O
X bx
ay
YB
b
ZB
aX
ay
O
XB
by
YB
a
b
a
bz
ZB
bx
b
W
ay
by
H
Y
by
Y
15. Проецирование отрезка прямой линии
ZZ
g"
V
a
V
az
A
a
a
b
bz
В
W
az
b
XB
a
b
O
X bx
ay
YB
ay
O
by
YB
a
b
b
ZB
aX
XB
f
a
bz
ZB
bx
b
W
ay
by
H
Y
by
Y
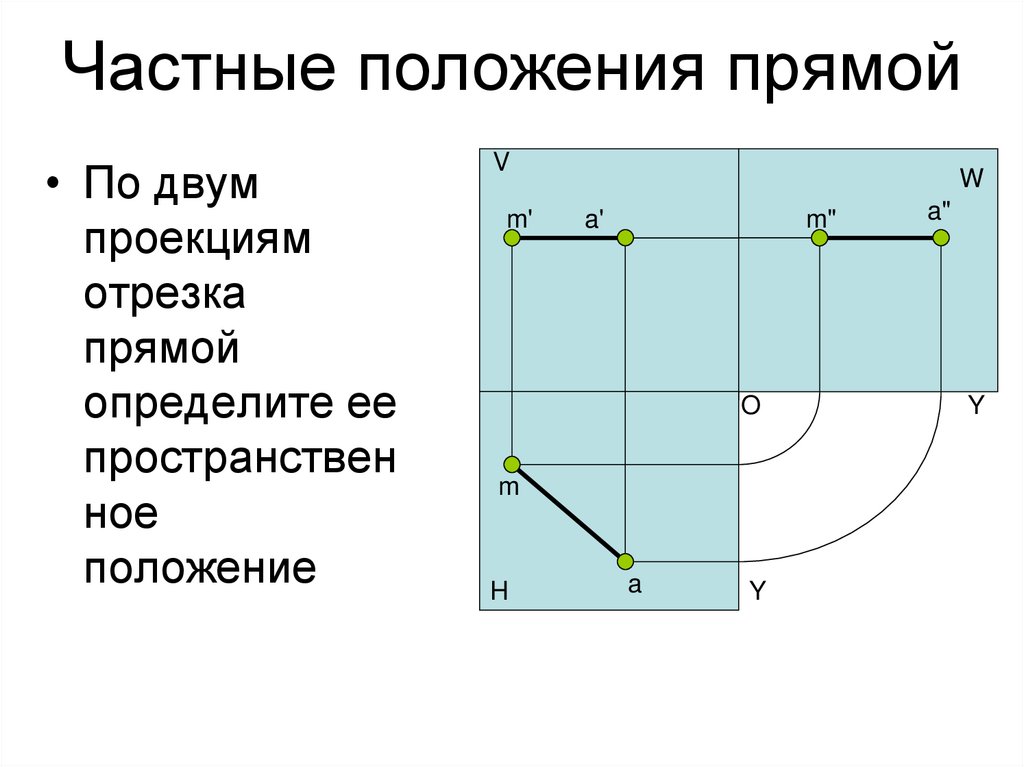
16. Частные положения прямой
• По двумпроекциям
отрезка
прямой
определите
ее
пространствен
ное
положение
Z
V
W
a
a
b
b
X
O
aΞb
H
Y
Y
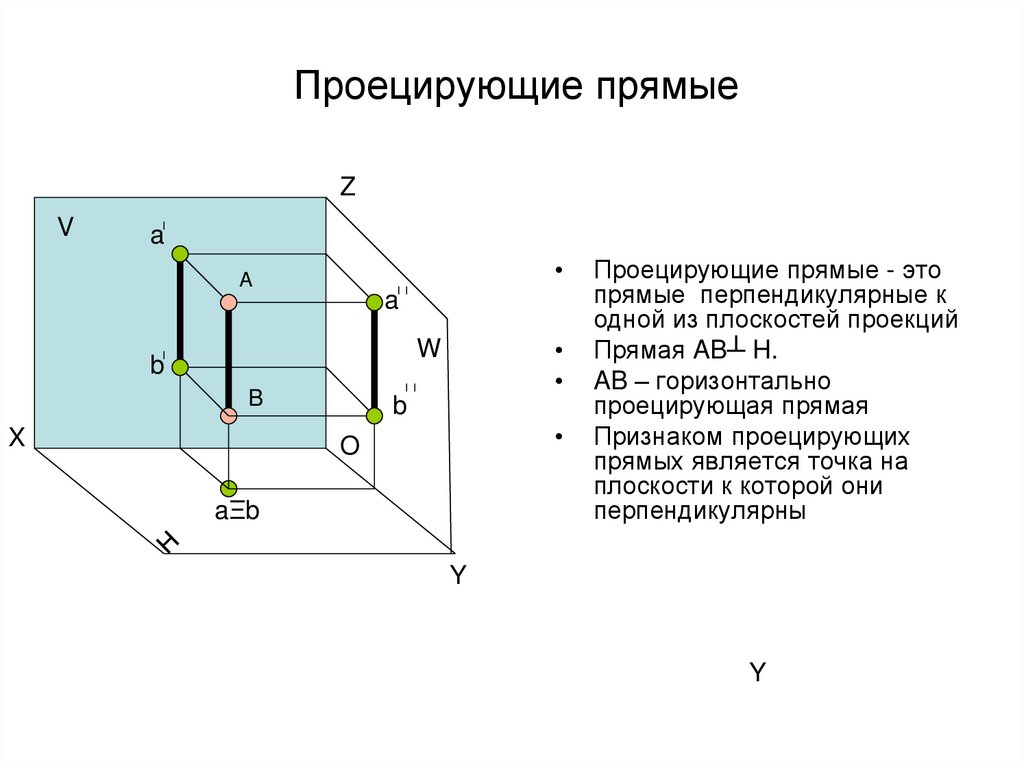
17. Проецирующие прямые
ZV
a
A
a
W
b
B
X
b
O
aΞb
Проецирующие прямые - это
прямые перпендикулярные к
одной из плоскостей проекций
Прямая AB┴ H.
AB – горизонтально
проецирующая прямая
Признаком проецирующих
прямых является точка на
плоскости к которой они
перпендикулярны
Y
Y
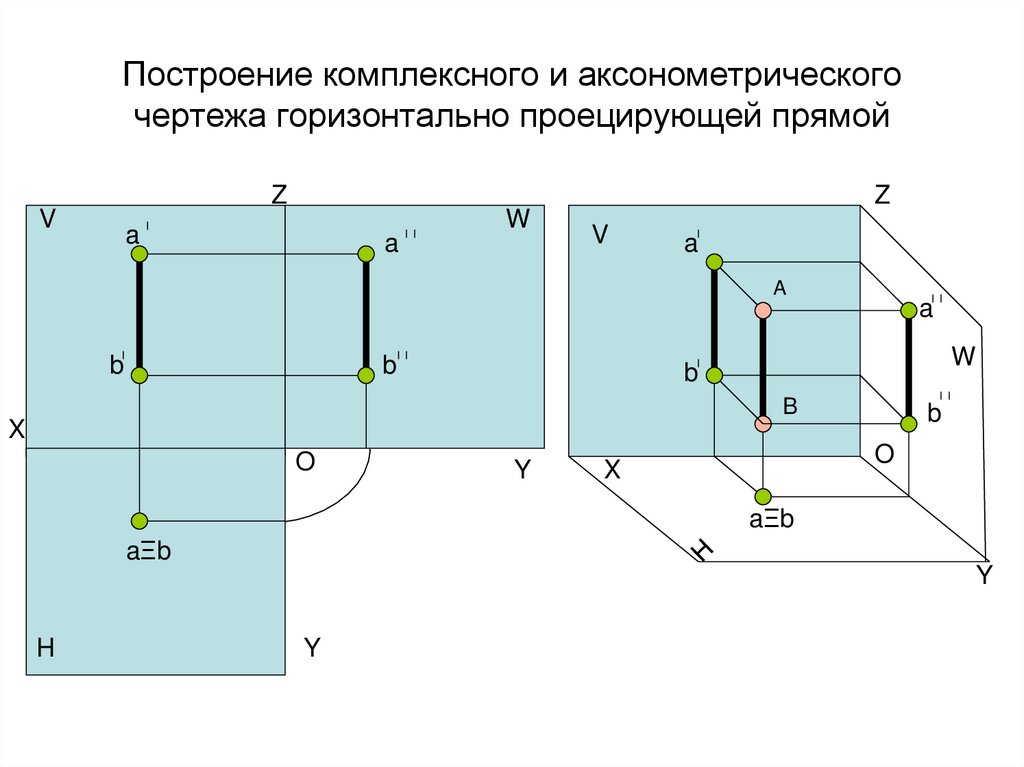
18. Построение комплексного и аксонометрического чертежа горизонтально проецирующей прямой
ZV
Z
W
a
a
V
a
A
b
b
a
W
b
B
b
X
O
Y
O
X
aΞb
aΞb
Y
H
Y
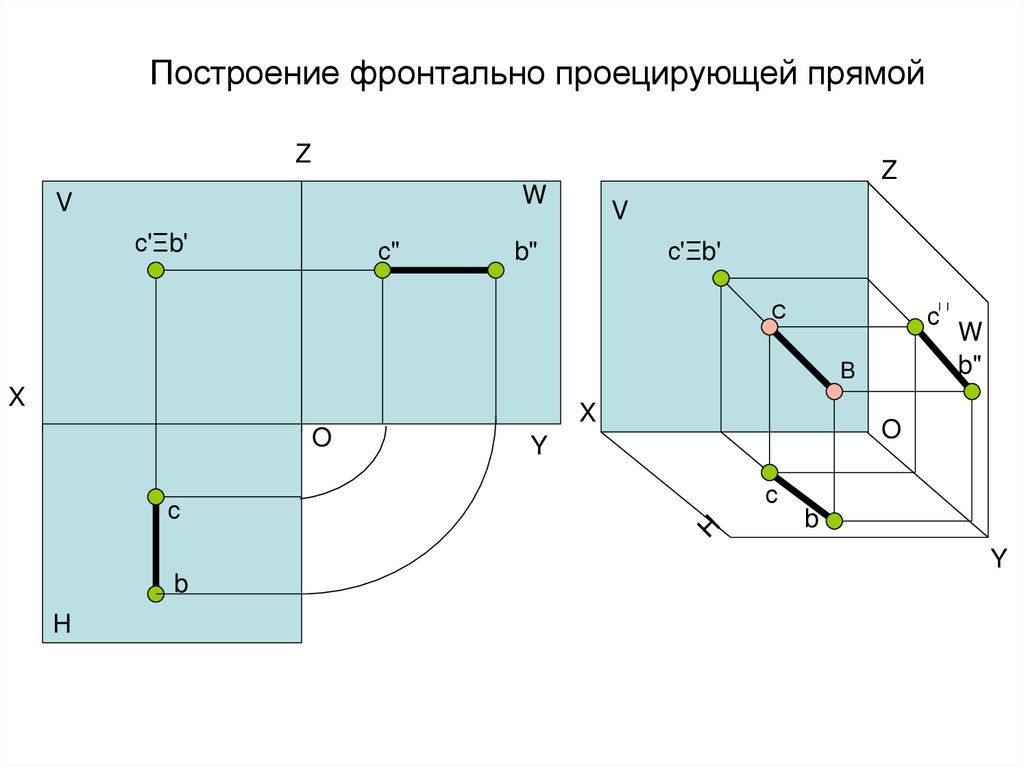
19. Построение фронтально проецирующей прямой
ZZ
W
V
с'Ξb'
с"
V
с'Ξb'
b"
С
с
B
X
X
O
с
W
b"
O
Y
с
b
Y
b
H
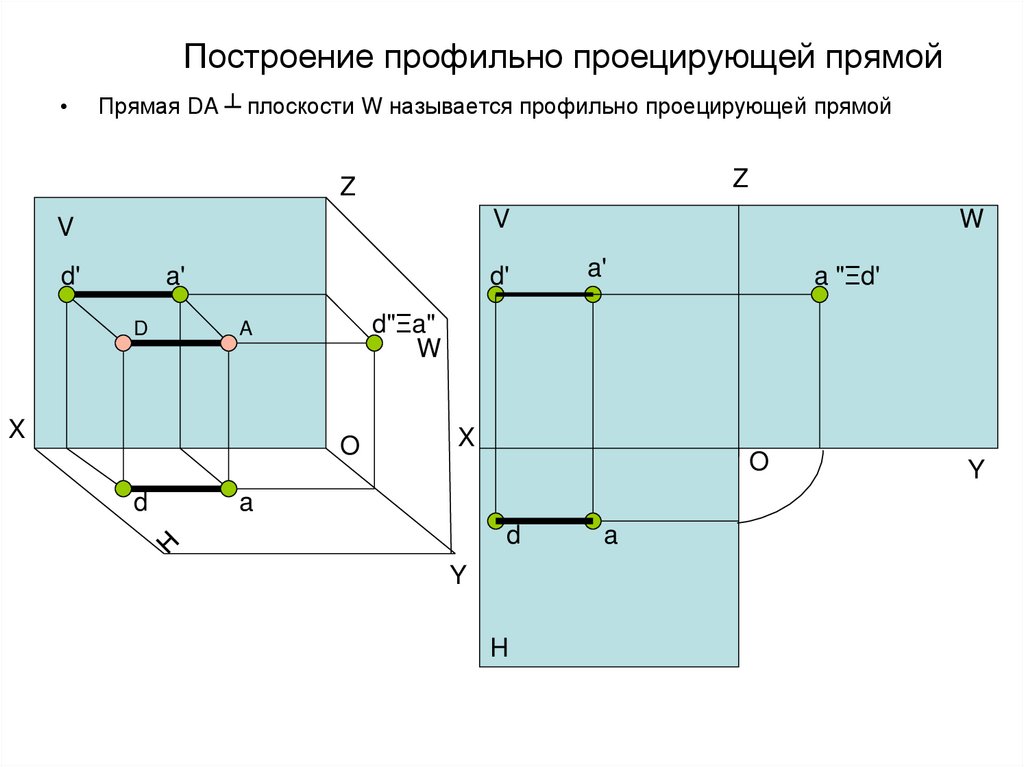
20. Построение профильно проецирующей прямой
Прямая DA ┴ плоскости W называется профильно проецирующей прямой
Z
Z
V
V
d'
a'
D
d'
O
d
a'
a "Ξd'
d"Ξa"
W
A
X
W
X
O
a
d
Y
H
a
Y
21. Построение профильно проецирующей прямой
•Прямая DA ┴ плоскости W называется профильно проецирующей прямойZ
Z
V
d'
V
W
a'
d'
a "Ξd"
a'
D
X
X
O
O
Y
d
d
d"Ξa"
W
A
a
a
Y
H
22. Частные положения прямой
• По двумпроекциям
отрезка
прямой
определите ее
пространствен
ное
положение
V
m'
W
a'
m"
O
m
H
a
Y
a"
Y
23. Построение комплексного и аксонометрического чертежа горизонтальной прямой
Прямая MA параллельна горизонтальной плоскости проекций, т.к высота точек М и А
одинаковая , т.е. координаты ZA = ZM. Такая прямая называется горизонталью
Z
Z
V
a'
m'
m"
W
a"
V
m'
ZM
a'
M
ZA
m" W
a"
A
Х
O
Y
X
O
m
m
a
Y
H
a
Y
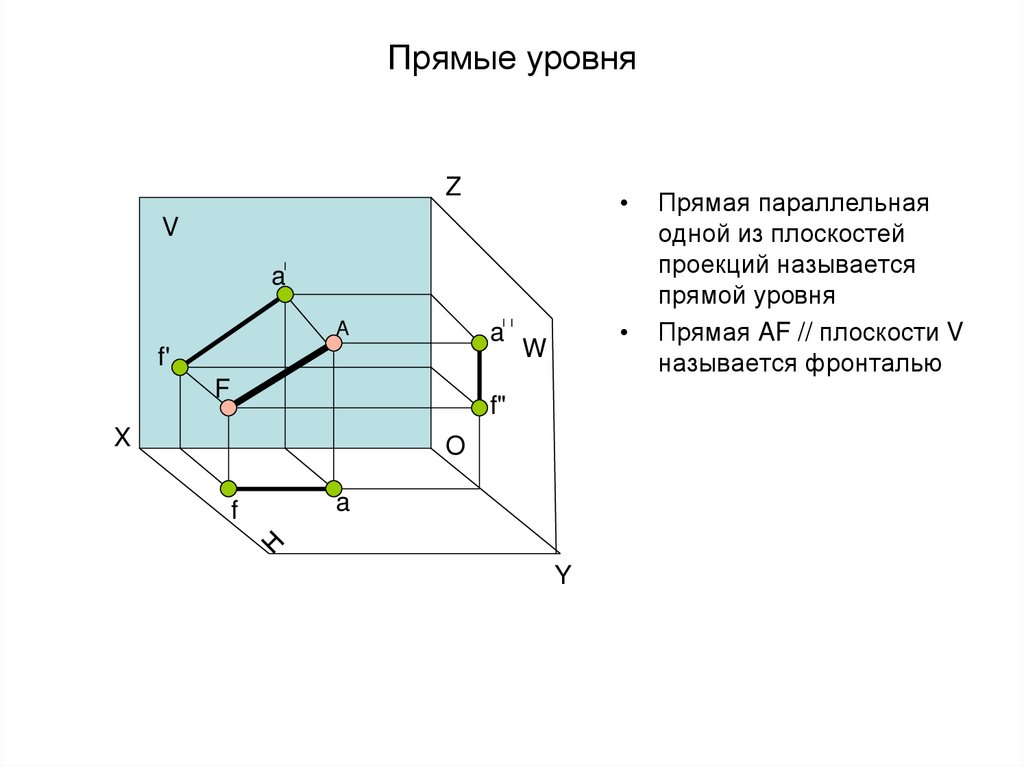
24. Прямые уровня
ZV
a
A
a
f'
F
W
f"
X
O
f
a
Y
Прямая параллельная
одной из плоскостей
проекций называется
прямой уровня
Прямая AF // плоскости V
называется фронталью
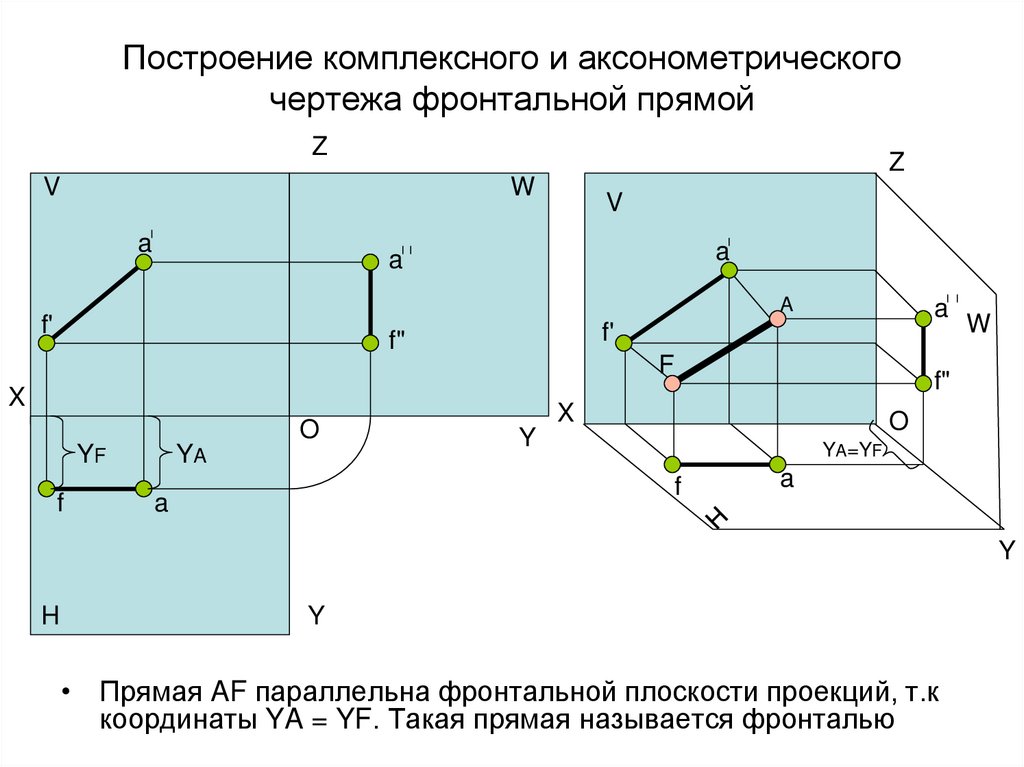
25. Построение комплексного и аксонометрического чертежа фронтальной прямой
ZZ
V
W
a
V
a
a
A
f'
a
f'
f"
F
X
O
YF
f
YA
f"
X
O
Y
YA=YF
f
a
W
a
Y
H
Y
• Прямая AF параллельна фронтальной плоскости проекций, т.к
координаты YA = YF. Такая прямая называется фронталью
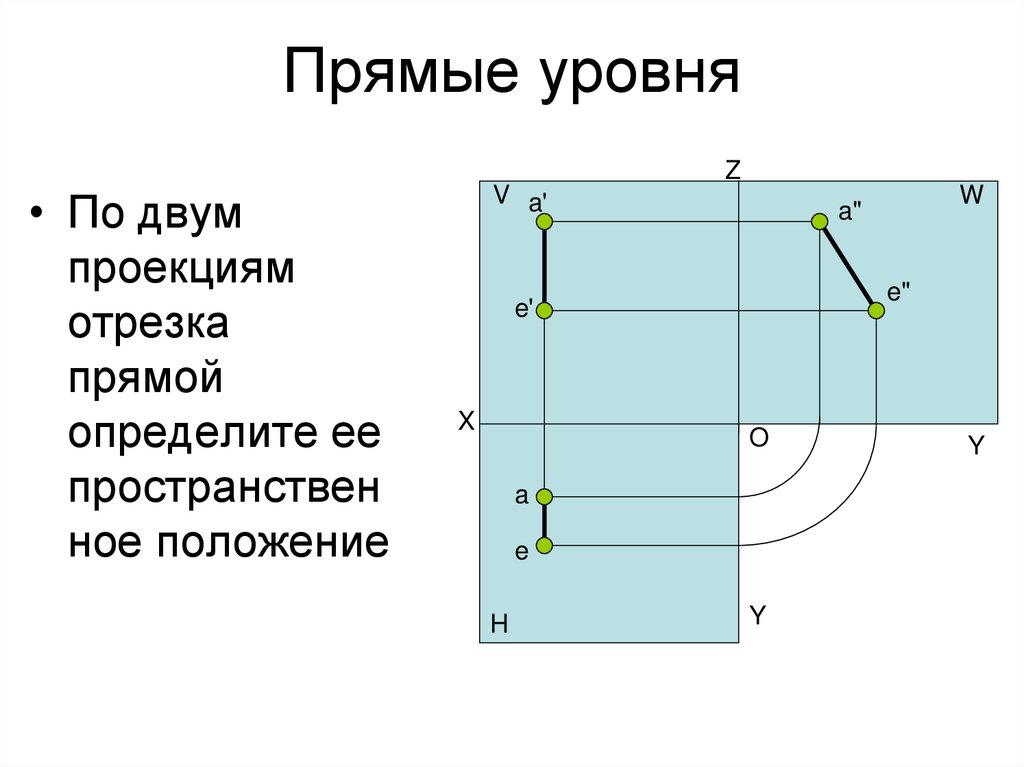
26. Прямые уровня
Z• По двум
проекциям
отрезка
прямой
определите ее
пространствен
ное положение
V a'
e"
e'
X
O
a
e
H
W
a"
Y
Y
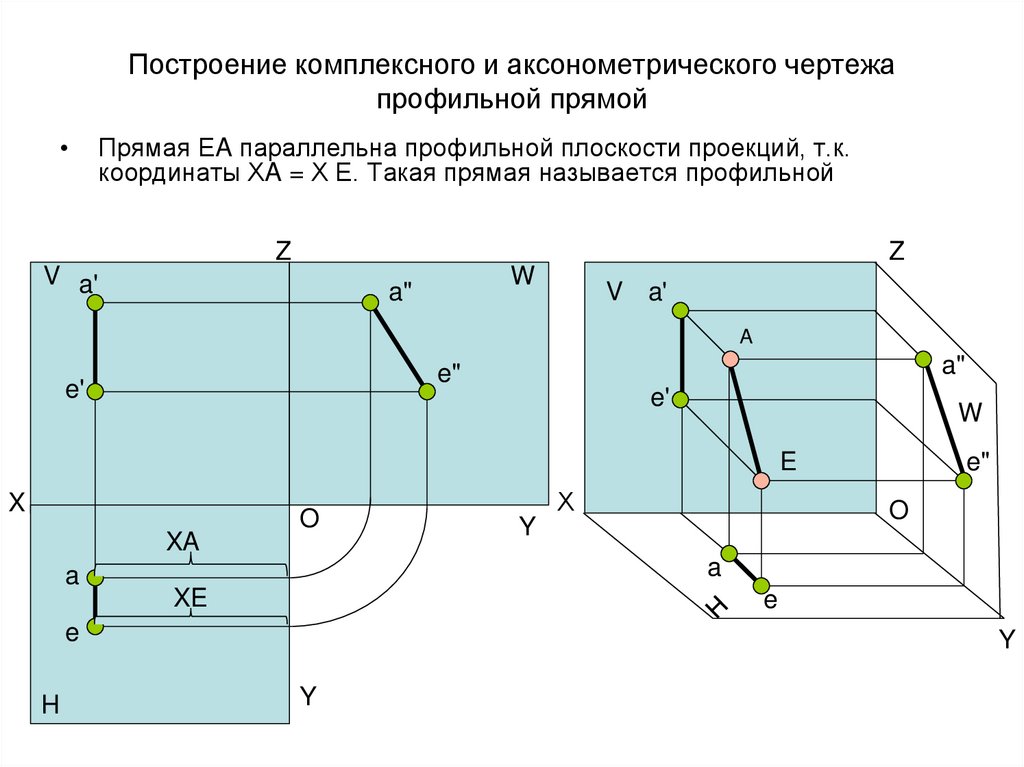
27. Построение комплексного и аксонометрического чертежа профильной прямой
Прямая ЕA параллельна профильной плоскости проекций, т.к.
координаты ХA = Х Е. Такая прямая называется профильной
Z
Z
V a'
W
a"
V a'
A
a"
e"
e'
e'
W
E
X
XA
a
O
O
Y
a
XE
e
e
H
Х
e"
Y
Y
28.
Построение третьей проекции каждой прямойZ
а'
k'
ℓ'
f‘=е'
b'
Х
О
f
k
ℓ
а=b
е
Y
Y
29.
Построение третьей проекции каждой прямойZ
f'
d'
k'
m'
n'
а'
О
X
n
m
а
d
k
f
Y
Y









 Инженерная графика
Инженерная графика








