Похожие презентации:
Формулы приведения
1.
2.
Если под знаком преобразуемойтригонометрической функции содержится
сумма аргументов вида π + t, π – t, 2π + t, 2π – t,
то наименование тригонометрической
функции следует сохранить.
3.
4.
5.
Любая из формул приведения может бытьзаписана и для градусной меры угла, то есть
когда под знаком тригонометрической
функции записано выражение вида
90° + α, 90° - α, 180° + α.
6.
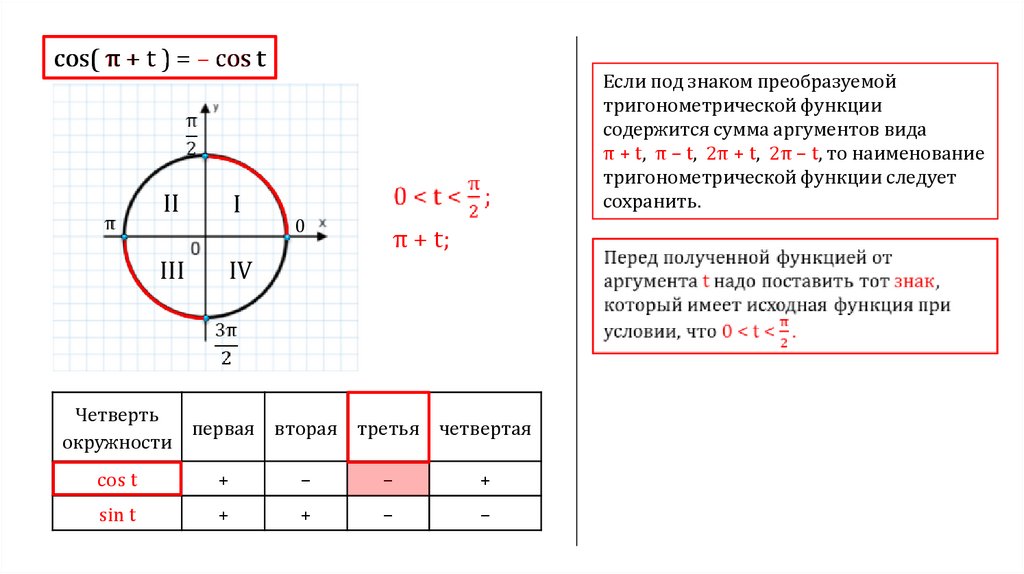
cos( π + t ) = – cos tII
I
III
Если под знаком преобразуемой
тригонометрической функции
содержится сумма аргументов вида
π + t, π – t, 2π + t, 2π – t, то наименование
тригонометрической функции следует
сохранить.
0
π + t;
IV
Четверть
первая вторая третья четвертая
окружности
cos t
+
–
–
+
sin t
+
+
–
–
7.
III
III
IV
0
Четверть
первая вторая третья четвертая
окружности
cos t
+
–
–
+
sin t
+
+
–
–
8.
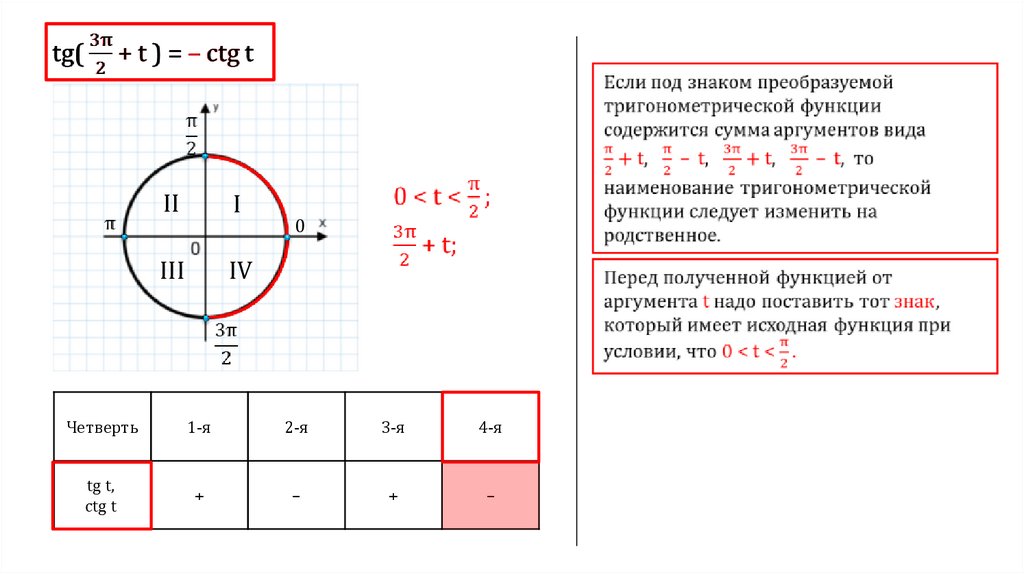
ЧетвертьII
I
III
IV
0
1-я
2-я
3-я
4-я
+
–
+
–
9.
ЧетвертьII
I
III
IV
Если под знаком преобразуемой
тригонометрической функции
содержится сумма аргументов вида π + t,
π – t, 2π + t, 2π – t, то наименование
тригонометрической функции следует
сохранить.
0
1-я
2-я
3-я
4-я
+
–
+
–
10.
Пример 1. Вычислить с помощью формул приведения sin ( –330° ).Решение.
sin ( –t ) = – sin t
sin ( – 330°) = – sin 330°;
sin ( – 330°) = – sin 330° = – sin ( 360° – 30°);
⟹ наименование функции сохраним;
330° = 360° – 30° — аргумент IV четверти;
Четверть
первая вторая третья четвертая
окружности
cos t
+
–
–
+
sin t
+
+
–
–
11.
Пример 1. Вычислить с помощью формул приведения sin ( –330° ).Решение.
sin ( – 330°) = – sin 330°;
sin ( – 330°) = – sin 330° = – sin ( 360° – 30°);
⟹ наименование функции сохраняем;
330° = 360° – 30° — аргумент IV четверти;
sin ( –t ) = – sin t
12.
Доказательство.⟹ меняем наименование функции на cos;
Четверть
первая вторая третья четвертая
окружности
cos t
+
–
–
+
sin t
+
+
–
–
13.
Доказательство.⟹ наименование функции сохраняем;
Четверть
первая вторая третья четвертая
окружности
cos t
+
–
–
+
sin t
+
+
–
–












 Математика
Математика








